 When its 19 triangles are Type A triangles, the 1-tree contains 251 yods. 19 yods are centres of these
triangles, leaving (251−19=232) yods. EHYEH, the Godname of Kether with number value 21,
prescribes this number because
When its 19 triangles are Type A triangles, the 1-tree contains 251 yods. 19 yods are centres of these
triangles, leaving (251−19=232) yods. EHYEH, the Godname of Kether with number value 21,
prescribes this number because| << Previous 1... 64 65 [66] 67 68 ...81 Next >> |
#66 The outer & inner Trees of Life as expressions of the permutational power of the tetractys
 When its 19 triangles are Type A triangles, the 1-tree contains 251 yods. 19 yods are centres of these
triangles, leaving (251−19=232) yods. EHYEH, the Godname of Kether with number value 21,
prescribes this number because
When its 19 triangles are Type A triangles, the 1-tree contains 251 yods. 19 yods are centres of these
triangles, leaving (251−19=232) yods. EHYEH, the Godname of Kether with number value 21,
prescribes this number because
1 + 2 + 3 +... + 21 = 232.
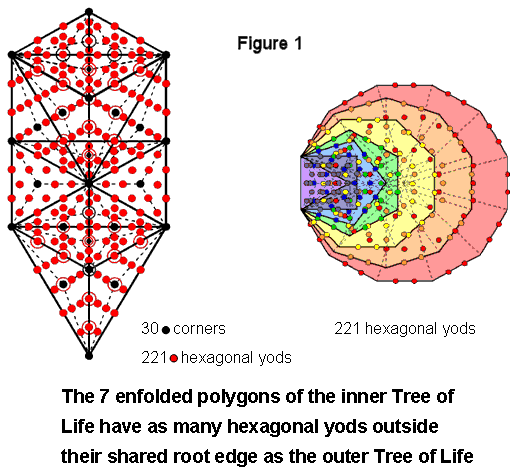
They include 11 corners that are located at SLs of the 1-tree, which is composed of (19+11=30) corners of (19×3=57) tetractyses and (251−30=221) hexagonal yods.
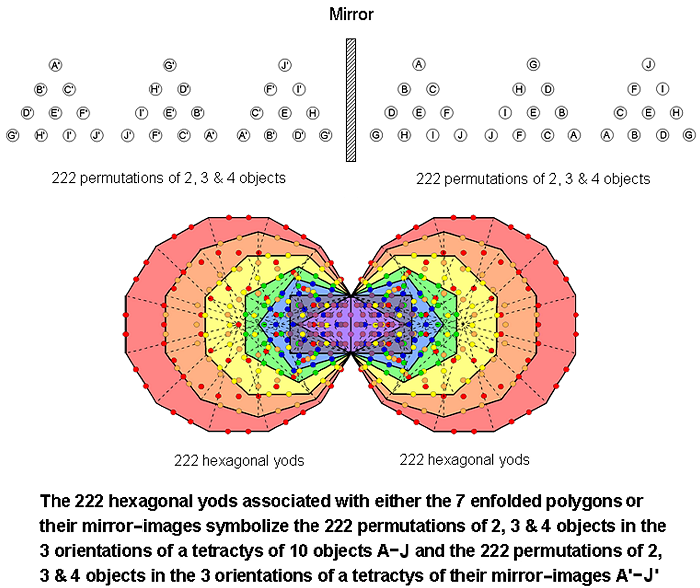
The seven enfolded polygons of the inner Tree of Life have 47 sectors. When the polygons are Type A, they contain 264 yods. Of these, 41 yods are corners of tetractyses, leaving (264−41=223) hexagonal yods. Two hexagonal yods lie on their shared root edge and (223−2=221) hexagonal yods are outside it. This is the number of hexagonal yods in the 1-tree (see diagram). 221 hexagonal yods in the other set of seven enfolded polygons lie outside the root edge as well. By associating one hexagonal on the root edge with one set and the other hexagonal yod with the other set, 222 hexagonal yods can be regarded as associated with each set. The Tetrad expresses the 444 hexagonal yods in both sets.
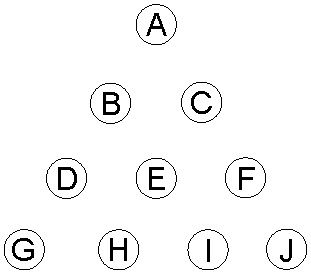
Consider a tetractys array of 10 objects A, B, C, D, E, F, G, H, I & J:
The number of combinations of r objects selected from n objects ≡ nCr = n!/r!(n−r)!. The number of permutations of r objects = r!. The number of permutations of r objects selected from n objects ≡ nPr = n!/(n−r)!. Table 1 below lists the numbers of combinations and permutations of objects selected from each row of a tetractys array:
Table 1. The numbers of combinations & permutations in the four rows of the tetractys.
|
n |
n |
Number of combinations of more than one object = 2n − 1 − n |
Number of permutations = n! |
n |
| 1 | 1 | 0 |
1 |
0 |
| 2 | 3 | 1 |
2 |
2 |
| 3 | 7 | 4 |
6 |
6 + 6 = 12 |
| 4 | 15 | 11 |
24 |
12 + 24 + 24 = 60 |
|
|
|
|
YAHWEH, the Godname of Chokmah with number value 26, determines the number of combinations of the 10 objects, taken one, two, three & four at a time. Their numbers in each row of the tetractys are tabulated below in Table 2:
Table 2. Numbers of combinations of objects in the rows of the tetractys.
|
Group of 1 |
Group of 2 |
Group of 3 |
Group of 4 |
Total |
|
| 1st row | 1 | 0 | 0 | 0 | 1 |
| 2nd row | 2 | 1 | 0 | 0 | 3 |
| 3rd row | 3 | 3 | 1 | 0 | 7 |
| 4th row | 4 | 6 | 4 | 1 | 15 |
| Total = | 10 | 10 | 5 | 1 | 26 |
YAH with number value 15 determines the number of combinations of the four objects in the fourth row, the number of combinations of one & three objects in the tetractys and the number of combinations of two & three objects in the tetractys. There are 16 combinations of two, three & four objects. They have 74 permutations. Including single objects, there are 84 permutations taken one, two, three & four at a time. The Tetrad Principle discussed in Article 1 determines this parameter of holistic systems because:
12 + 32 + 52 + 72 = 84.
It is the number of yods surrounding the centre of a 2nd-order tetractys (see here). Indeed, the Tetrad Principle determines the tetractys as the fourth triangular number. The first four of these triangular arrays have 90 permutations of two, three & four dots taken from their rows:
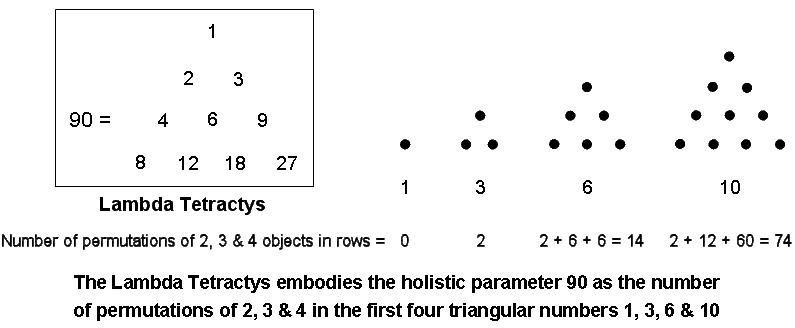
This is the sum of the 10 integers making up the Lambda Tetractys (its first discussion is here). Given the evidence presented in this website for the Lambda Tetractys and the Tetrahedral Lambda being the arithmetic version of sacred geometries, the appearance of the holistic parameter 90 is evidence for the archetypal status of the first four triangular numbers. This is hardly surprising, given that the tetractys is a representation of the Tree of Life. There is one pair of dots taken from the single row of the second triangular number, four pairs from the two rows of the third and 10 pairs from the three rows of the fourth. The 15 pairs have (15×2!=30) permutations. There is one set of three dots in the third triangular number and five sets of three in the fourth number. The six sets of three dots have (6×3!=36) permutations. There is one set of four dots in the fourth triangular number with (4!=24) permutations. Hence, the 90 permutations consist of 36 permutations of three dots and (30+24=54) permutations of two & four dots. This 36:54 division manifests in the archetypal pattern of the Lambda Tetractys because the sum of the integers at its three corners is 36 and the sum of its remaining seven integers is 54. The six permutations of pairs of dots in the third row of the tetractys of 10 dots may be understood to correspond to the number "6" at the centre of the Lambda Tetractys. It leaves (30−6=24) permutations of two dots and 24 permutations of four dots, i.e., 48 permutations. The sum of the integers at the six corners of a hexagon in the Lambda Tetractys is 48. This is a parameter of holistic systems (see here), being the number value of Kokab, the Mundane Chakra of Hod. Its 24:24 division that is so characteristic of these systems manifests in the set of 24 permutations of two dots and the 24 permutations of four dots.
The 30 permutations of two dots in the rows of the first four triangular numbers contain (30×2=60) dots, the 36 permutations of three dots contain (36×3=108) dots and the 24 permutations of four dots contain (24×4=96) dots. The 90 permutations of two, three & four dots in these four triangular numbers contain (60+108+96=264) yods. This number is another parameter of holistic systems, being the number of yods in the seven enfolded polygons of the inner Tree of Life:
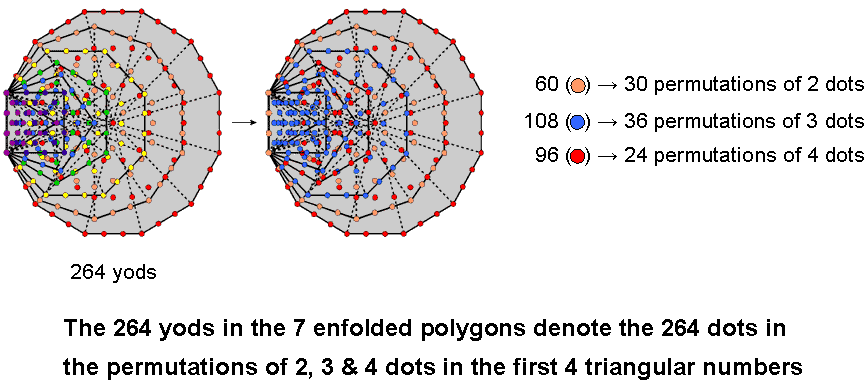
It provides excellent support for the Tetrad Principle, which states that numbers in the first four members of a class of mathematical objects (including types of numbers, such as triangular numbers) is a parameter of holistic systems. The numbers of yods in the seven enfolded polygons are listed below:
| Triangle | Square | Pentagon | Hexagon | Octagon | Decagon | Dodecagon |
| 15 | 21 | 27 | 27 | 45 | 60 | 69 |
(all numbers except for the decagon are the numbers of yods outside the root edge; notice that the centre of the hexagon coincides with a corner of the triangle and that the centre of the decagon coincides with a corner of the pentagon). We see that the 60 orange yods in the decagon denote the 60 dots making up the 30 permutations of two dots, the 108 blue yods in the triangle, square, pentagon & octagon denote the 108 dots making up the 36 permutations of three dots and the 96 red yods in the hexagon & dodecagon denote the 96 dots in the 24 permutations of four dots. Amazingly, different sets of enfolded polygons can be found that contain the same numbers of yods as the numbers of dots making up permutations of two, three & four dots in the first four triangular numbers. Unless one believes in miracles, this cannot be due to chance.
The permutations in the three orientations of a tetractys of objects
Referring to
the last column in the first table shown above, there is one permutation of A, (2+2=4) permutations of B &
C, taken one or two at a time, (3+12=15) permutations of D, E & F taken one, two or three
at a time and (4+60=64) permutations of G, H, I & J taken one, two, three or four at a
time. Among the 74 permutations of two, three & four objects in the last three rows are the 16 combinations
of these groups shown in the second column, so that they have (74−16=58) permutations.
The tetractys has three orientations generated by rotating it so that each side becomes its base. Each orientation provides 16 new combinations and 74 new permutations of two, three or four objects. These orientations generate (3×16=48) such combinations and (3×74=222) permutations. Including the 10 permutations/combinations that are the single objects themselves (which, of course, are the same for each orientation), the three possible orientations generate (10+48=58) combinations and (10+222=232) permutations of one, two, three or four objects taken from the rows of the rotated tetractyses. The 222 permutations consist of 174 permutations of the 48 basic combinations of two, three & four objects.
Comparing these results with the yod populations of the 1-tree and its inner form, we see that the 232 yods in the 1-tree that are not centres of its 19 triangles denote the 232 permutations of the objects in the three orientations of the tetractys array. The 10 yods that are Sephiroth of the 1-tree per se denote the 10 objects themselves and the 222 yods other than centres of triangles denote their 222 permutations, taken two, three or four at a time from the three orientations. In terms of the equivalence of the tetractys to the Tree of Life, its central yod denotes Malkuth. The 232 yods in the 1-tree consist of Malkuth, its lowest point, and 231 yods above it. In the same way, the 232 permutations consist of the single object E occupying the centre of the tetractys and the 231 permutations other than this of all sets of objects in the rows of the three tetractyses. The 222 hexagonal yods associated with a set of seven enfolded polygons of the inner Tree of Life denote the 222 permutations of two, three & four objects. They comprise a hexagonal yod on the root edge and 47 hexagonal yods at centres of tetractyses, i.e., 48 hexagonal yods, and 174 hexagonal yods on sides of tetractyses. Compare this with the 48 combinations of two, three or four objects in the three orientations of a tetractys and their 174 permutations. The hexagonal yods denote all possible permutations of objects selected from the rows of these three tetractyses. It is amazing confirmation of the equivalence of the Tree of Life and the tetractys — not only merely conceptually as representations of holistic systems but in terms of the tetractys geometry of the 1-tree expressing the power of permutation inherent in the tetractys.
Another illustration of this is as follows: in the discussion in #43 of how sacred geometries embody the number 236, we found that 236 yods line the sides of the (7+7) enfolded polygons of the inner Tree of Life. Therefore, 232 yods line their sides outside the root edge, which has four yods. In other words, the number 232 determines, starting from the root edge, the shape of the inner Tree of Life in terms of the boundaries of each polygon:
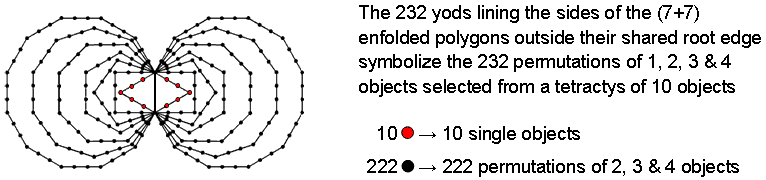
The ten red yods that line the two enfolded triangles outside the root edge symbolize the 10 single objects themselves, and the 222 black yods lining the sides of the other 12 polygons symbolize the 222 permutations of two, three & four objects picked from the rows of the three tetractyses. The shape of the inner Tree of Life quantifies the number of permutations of all possible selections from the three orientations of a tetractys of objects. It also determines their 48 possible combinations because the table indicates that they consist of (3×10=30) groups of two, (3×5=15) groups of three and (3×1=3) groups of four, which should be compared with the 48 corners of the seven separate polygons, the octagon, decagon & dodecagon having 30 corners, the square, pentagon & hexagon having 15 corners and the triangle having three corners.
The first six polygons of the inner Tree of Life constitute a holistic subset of the whole set of seven polygons. Enfolded, they have 26 corners prescribed by YAHWEH (ELOHIM prescribes the 50 corners in both sets). When separate, they have six centres, 36 corners, where 36 is the number of the Godname ELOHA of Geburah, the sixth Sephirah of Construction, and 180 hexagonal yods — a total of 222 yods:
216 yods surround the centres of the first six polygons, where 216 is the number value of Geburah. Compare these properties with the fact that, according to the last column in the table of numbers of permutations, the 74 permutations of two, three & four objects consist of two permutations of the two objects B & C in the second row of the tetractys, 12 permutations of D, E & F in the third row and 60 permutations of G, H, I & J in the fourth row. The three orientations have (3×2=6) permutations of two objects in the second rows, (3×12=36) permutations in the third rows and (3×60=180) permutations in the fourth rows. The numbers of the three types of yods denote the numbers of permutations of the objects in the three rows of the three tetractys arrays of objects.
It has been shown that the seven enfolded polygons and the six separate polygons in half the inner Tree of Life embody the number of permutations of the three possible orientations of a tetractys of 10 objects. What about the other half of the inner Tree of Life? The fact that the two halves are mirror-images of each other provides the clue to what it embodies. If each object is not identical to its mirror-image, a new array of objects can be generated by reflecting the tetractys in a mirror, so that object A→A′, B→B′, etc. The permutations in the mirror-images of each array (as opposed to each array of the mirror-images of objects) are identical to their counterparts in each array. This means that a new set of three tetractyses can be created only if the objects themselves are chiral. (Alternatively, instead of a purely geometric context, objects may be considered that posses an intrinsic polarity — positive and negative. In the present discussion, the term "mirror-image" will be used to distinguish the two opposite types of object, but it should not be taken literally, just as the two mirror-image halves of the inner Tree of Life do not always refer to mirror reflections when applied to some holistic systems, e.g., the rising and falling intervals between musical notes. For convenience, terms such as "reflection" and its associated words will be retained; this terminology, too, should be understood in a general sense, not in a literal one). As the reflection does not affect the numbers of permutations in each row of the tetractys, there are 74 permutations of the 10 mirror-image objects A′–J′. The reflected array of objects has three orientations, so that there are, likewise, 222 permutations of these objects. They correspond to the 222 hexagonal yods that are associated with the mirror-image set of seven enfolded polygons:
The 444 permutations consist of 12 permutations of two objects and their mirror-images in
the second rows, 72 permutations of two or three objects in the third rows and 360
permutations of two, three or four objects in the fourth rows. The second & third rows generate
(12+72=84) permutations, which we saw above is the number of permutations of one, two, three
& four objects in a tetractys of objects. The two enfolded squares have 38 hexagonal yods and the two
enfolded pentagons or the two enfolded hexagons have 46 hexagonal yods. The pair of enfolded squares &
pentagons/hexagons contain (38+46=84) hexagonal yods and the remaining 10 enfolded polygons have 360 hexagonal
yods. Once again, the geometry of the inner Tree of Life matches the permutational properties of a tetractys of
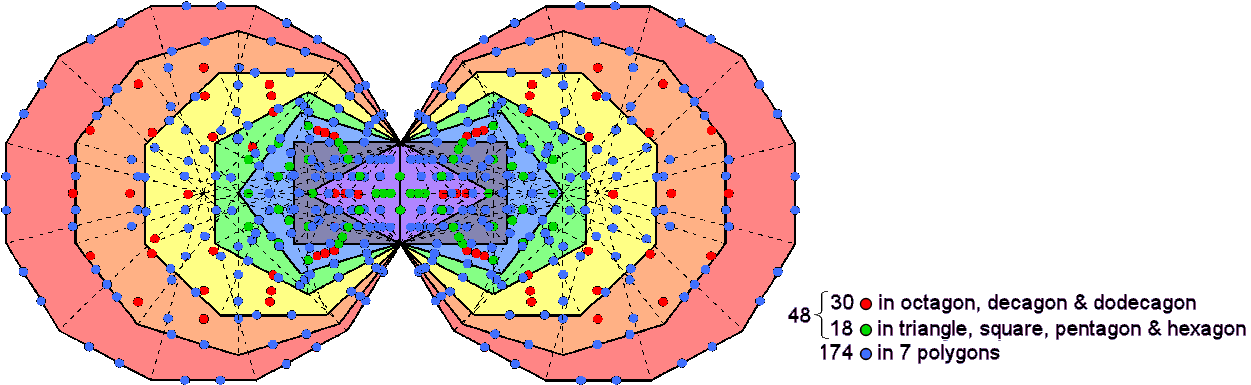
objects — even when the objects are chiral or possess some kind of polarity that need not be specified here. This is confirmed for the basic 3:7 distinction in a tetractys considered earlier, which generates 48 permutations purely of the seven objects and 174 permutations involving corners. It was found that the former comprise 30 permutations of two and 18 permutations of three. The 48 permutations are symbolised in the diagram above by the hexagonal yod on the root edge associated with one set of enfolded polygons and the 47 hexagonal yods at centres of tetractyses. The sectors of the octagon, decagon & dodecagon have 30 red hexagonal yods at their centres and the remaining four polygons have 17 green hexagonal yods at the centres of their sectors. This 3:4 division in the polygons corresponds to the difference between the permutations of two objects and permutations of three objects that belong to the set of seven, the 3:7 division in the tetractys itself corresponding to the distinction between the 174 blue hexagonal yods on sides of the tetractyses in the polygons and the 48 hexagonal yods made up of the one associated with them on the root edge and the 47 at their centres.
The holistic parameters 192 & 384
The third row of the tetractys of ten objects A–J is made up of the objects D, E & F, where E is the centre
of the array. They form the following permutations of two and three objects:
DE, ED, EF, FE, DF, FD, DEF, DFE, EFD, EDF, FDE & FED.
Ten permutations contain the central object E and two permutations do not. As there are 74 permutations of two, three & four objects selected from the four rows, (74−10=64) permutations do not contain the central object, where 64 is the number value of Nogah, the Mundane Chakra of Netzach. This would, of course, be true if the missing object were any one of those in the third row. However, the central object has a special significance because, in terms of the equivalence of the Tree of Life and the tetractys, the central dot in the latter symbolizes Malkuth, the last Sephirah. The objects need not be identified as Sephiroth. Provided, however, that rules exist for associating each object with a particular Sephirah, we can conclude that the nine members of the tetractys associated with the nine Sephiroth above Malkuth have 64 permutations when grouped in sets of two, three & four. This means that the three orientations of the tetractys, in each of which object E does not alter its position because it remains the centre, generate (3×64=192) permutations that do not contain it. As #59 demonstrates, the number 192 is a defining parameter of sacred geometries (see its general discussion here). The three tetractyses composed of A′–J′, the mirror-images of the objects A–J, generate 192 permutations. The 18 distinct types of objects other than E and its mirror-image E′ that make up the six tetractyses generate (192+192=384) permutations. This, too, is a characteristic pattern of sacred geometries, as is the factorization 192 = 64×3. For example, the table of 64 hexagrams consulted by practitioners of the ancient Chinese I Ching system of divination consists of two sets of 64 trigrams, each trigram being three rows of either lines or broken lines. The three orientations of the tetractys correspond to this three-fold pattern, whilst the I Ching counterpart of mirror-objects is the fact that each diagonal half of the square array of trigrams is the mirror image of the other, with the mirror lying along its diagonal. Another example is the set of 64 codons of mRNA and the 64 anticodons of tRNA (see Article 46). The three nitrogen bases in a codon correspond to the three orientations of the tetractys and the complementarity between the two bases A & U and between the two bases C & G, which bond to each other in each case by hydrogen bonding, is an example of what has here been called "mirror-images." In fact, they denote the positive electrical polarity of the protons in their hydrogen atoms and the negative polarity of their oxygen & nitrogen atoms due to their unshared electrons, which binds complementary base molecules by electrostatic forces). The global parameter 384 found in sacred geometries (see here & here), in DNA as the 384 instances of the four types of nitrogen bases in the 64 codons and the 64 anticodons, and in the seven diatonic musical scales as the 384 ascending & descending intervals between their notes (see here), quantifies the potential of a single tetractys of objects to generate all permutations of its non-central members.
Suppose that, instead of selecting all possible groups of objects within each row and then working out their permutations, we consider only each row as a whole. The row of two objects has (2!=2) permutations, the row of three objects has (3!=6) permutations and the row of four objects has (4!=24) permutations. These three rows have (2+6+24=32) permutations. The three orientations of the tetractys have (3×32=96) permutations of the sets of two, three & four objects. The three orientations of the tetractys array of the
The (118+118) yods lining the 83 sides of the (7+7) enfolded polygons symbolise the (118+118)
objects
that make up the (32+32=64) permutations of the rows of 2, 3 & 4 objects arranged in two
tetractyses.
objects B′–J′ have 96 analogous permutations. Both sets of tetractyses have (96+96=192) permutations. The holistic parameter 192 re-appears as the number of permutations of the second, third & fourth rows in the three orientations of a tetractys of objects and a tetractys of their mirror-images. The 32 permutations for each orientation are composed of (2×2 + 6×3 + 24×4 = 118) objects, so that 236 objects make up the (32+32=64) permutations in a tetractys and a tetractys of its mirror objects. This is the number of yods lining the (7+7) enfolded polygons of the inner Tree of Life.
We found earlier that a tetractys of objects has 74 permutations when subsets of objects within each row are considered. Hence, those subsets have (74−32=42) permutations, i.e., (3×42=126) permutations for all three orientations. Therefore:
222 = 96 + 126.
The numbers of hexagonal yods associated with the seven enfolded polygons are:
|
Root edge |
Triangle |
Square |
Pentagon |
Hexagon |
Octagon |
Decagon |
Dodecagon |
Total |
|
| Number of hexagonal yods = |
1 |
13 |
18 |
23 |
23 |
38 |
48 |
58 |
222 |
The octagon & dodecagon have 96 hexagonal yods and the remaining five polygons (including the one associated with them on the root edge) have 126 hexagonal yods. They symbolize, respectively, the 96 permutations of two, three & four objects in the three orientations of a tetractys and the 126 permutations of their subsets. We saw earlier that the 222 permutations are also symbolized by the 222 yods lining the last (6+6) enfolded polygons. The numbers of yods lining pairs of such polygons are tabulated below in Table 3:
Table 3. Numbers of yods lining pairs of similar polygons in the last (6+6) enfolded polygons.
|
2 Squares |
2 Pentagons |
2 Hexagons |
2 Octagons |
2 Decagons |
2 Dodecagons |
Total |
|
| Number of yods lining sides outside root edge = |
16 |
22 |
28 |
40 |
52 |
64 |
222 |
96 yods line the sides of the pairs of squares, hexagons & decagons and 126 yods line the sides of the pairs of pentagons, octagons & dodecagons. Once again, the non-trivial fact emerges that subsets of polygons exist generating the same division of numbers of boundary yods as that existing between permutations of whole rows in the three orientations of a tetractys and permutations of their subsets.
Number of objects in 222 permutations of 2, 3 & 4 objects in tetractys
The
number of permutations of r objects selected from n objects = nPr = n!/(n−r)!. Each
permutation contains r objects. The number of objects needed to make these permutations =
rnPr. Below in Table 4 are tabulated the numbers of objects in the permutations of the
objects in the second, third & fourth rows of a tetractys of objects:
Table 4. Numbers of objects in permutations of 2-4 objects in the rows of the tetractys.
|
n |
n |
| 2 | 2×2 = 4 |
| 3 | 2×6 + 3×6 = 12 + 18 = 30 |
| 4 | 2×12 + 3×24 + 4×24 = 96 + 96 = 192 |
|
Total = 226 |
|
The table indicates that the 24 permutations of the four objects in the fourth row of the tetractys contain 192 objects made up of the 24 objects in the 12 permutations of two objects, the 72 objects in the 24 permutations of three objects and the 96 objects in the 24 permutations of four objects, i.e., (72+96=168) objects in the (24+24=48) permutations of three & four objects. The division:
192 = 24 + 168
is characteristic of holistic systems (see here under the heading "192 = 24 +168"). Each of the four objects in the fourth row appears 48 times (24 times in permutations of two & three objects and 24 times in permutations of all four objects). The fourth row of a tetractys is, of course, not a holistic system per se. However, it has been known for many centuries that its four dots symbolize the four vertices of a tetrahedron (the first Platonic solid) because the tetractys was regarded as symbolizing the sequence of a point, straight line, triangle & tetrahedron, the rows of one, two, three & four dots denoting the points that make them. Indeed, that was about the only meaning historians of mathematics ever gave to the tetractys! The 60 permutations of these four dots represent all possible orderings of subsets of two, three & four vertices of a tetrahedron. In view of the Tetrad Principle, it is not surprising, therefore, that holistic parameters like 192 and 48 should appear in what, historically, has symbolised the fourth member of the class of mathematical object known as the "n-simplex," (n= 0, 1, 2, 3, etc), the tetrahedron being the 3-simplex.
Regarding the 10 single objects that form the tetractys as their own permutations, there are (226+10=236) objects in all 84 permutations of the 26 possible combinations of objects in the four rows. As pointed out earlier, this is the number of yods that line the sides of the (7+7) enfolded polygons of the inner Tree of Life — an amazing connection between the intrinsic permutational power of the tetractys and the geometry of the inner Tree of Life. Two objects have (2!=2) permutations with (2×2=4) objects, three objects have (3!=6) permutations with (6×3=18) objects and four objects have (4!=24) permutations with (24×4=96) objects. Therefore, the 226 objects making up the 74 permutations of the objects in the second, third & fourth rows of a tetractys comprise (4+18+96=118) objects in the 32 permutations of two, three & four objects and 108 objects in the 42 permutations of two objects selected from the third & fourth rows and three objects selected from the fourth row. The 222 permutations of two, three & four objects in the three orientations of a tetractys contain (226×3=678) objects that consist of (118×3=354) objects in the (32×3=96) permutations of two, three & four objects and (108×3=324) objects in the (42×3=126) permutations of two objects selected from third & fourth rows and three objects taken from fourth rows.
The (7+7) enfolded Type B polygons have 1370 yods (see here). Each set of seven enfolded Type B polygons contain 687 yods, i.e., 685 yods are associated with each set. (685−7=678) such yods surround the centres of the seven polygons, creating their shapes. The 678 yods surrounding centres that are associated with one set of seven Type B polygons symbolize the 678 objects making up the 222 permutations symbolized by the 222 hexagonal yods associated with this set when the polygons are Type A. The 678 yods in the other set of polygons that are their mirror-images symbolize the 678 mirror-image objects making up the 222 permutations in a tetractys of mirror-image objects. The decagon and the dodecagon have 324 yods surrounding their centres if the two yods in the root edge associated with either set of seven polygons are included. The first five enfolded polygons in the set of seven polygons have 354 yods surrounding their centres. The last two polygons determine the 324 objects in permutations of two and three objects and the first five polygons determine the 354 objects in permutations of two, three & four objects. Shown below is the inner Tree of Life counterpart of the objects making up permutations selected from a tetractys of 10 objects and a tetractys of its mirror-image objects (black yods are centres of polygons; all yods belonging to a polygon have the same colour):
The object E at the centre of the tetractys can be grouped in pairs with the two
other objects D & F in the third row. Their four permutations contain eight objects that comprise four
instances of E and four instances of these two objects. Groups of E, D & F form six permutations, each
including E once. The (4+6=10) permutations include the object E (4+6=10) times and the two other objects (4 +
6×2 = 16) times. Hence, the 10 permutations containing E comprise (10+16=26) objects. YAHWEH with number value 26 prescribes the number of objects appearing
in the permutations that contain E. Notice that this is similar to the combinatorial power of the complete
tetractys, which consists of 10 single objects and 16 combinations of two, three & four objects. The three
orientations of the tetractys generate 30 permutations containing (3×26=78) objects consisting of (3×10=30) objects E
and 48 objects D
& F. Both sets of three orientations generate (30×2=60) permutations containing (78×2=156) objects that
comprise (30×2=60) objects E and (48×2=96) objects D & F. The number 156 is the 155th integer after 1. We see that the number
value 155 of ADONAI
MELEKH, the complete Godname of Malkuth, is the number of objects making up all permutations of the row
containing the central object E. This is highly significant because, in terms of the correspondence between the
10 yods in the tetractys and the 10 Sephiroth of the Tree of Life (see here), the central yod corresponds to Malkuth. It is made even more
significant by the fact that 156 is the sum of all possible combinations of the values of the three types of
letters (yod, he & vav) in YHVH (יהוה), the famous Hebrew Name of God, whose number value
26 is the number of objects
in the 10 permutations that contain the central object:
YHVH = 26.
Y = 10, H = 5, V = 6.
| Y + H + V = | 21; |
| YH + YV + HV + HH = | 52; |
| YHV + YHH + HVH = | 57; |
| YHVH = | 26; |
| TOTAL = | 156. |
The last polygon in the inner Tree of Life is the dodecagon. It has 156 hexagonal yods when it is Type B (see its discussion here). 155 hexagonal yods are associated with each of the two enfolded Type B dodecagons in the inner Tree of Life:
The significance of the number 156 for the outer Tree of Life is that it is the number of yods other than the 10 Sephirothic white corners that line its 16 triangles when they are Type A:
(circles around dots denote yods that are behind other yods in the line of sight of the observer). The 60:96 division of objects making up the 60 permutations (60 objects E, 96 objects D & F) containing E has its counterpart in the Tree of Life as:
1. the 60 yods made up of the 44 hexagonal yods lining the 22 sides of its 16 triangles and the 16 corners of tetractyses at their centres;
2. the 96 hexagonal yods lining the (3×16=48) sides of tetractyses inside these triangles.
Holistic patterns in the permutations of objects
The 192 permutations of objects other than the central one selected from the rows of the three orientations of a tetractys array consist of the 64 permutations generated by each orientation. The factorisation: 192 = 64×3 is characteristic of holistic systems embodying this number. As mentioned earlier, the most conspicuous example of this pattern is the set of 64 trigrams with 192 lines & broken lines that make up each diagonal half of the 8×8 square array of 64 hexagrams used in the I Ching system of divination. Their counterparts are the 192 permutations in the three orientations of the tetractys of objects A-J and the 192 permutations in the three orientations of the tetractys array of what has been called their "mirror-image" objects Aʹ-Jʹ. The 64 codons and 64 anticodons, each with 192 instances of the four nitrogen bases A, U, G & C, are the biological manifestation of this universal pattern. Other patterns displayed by holistic systems are:
1. 192 = 24 + 168 (e.g., the 24 lines & broken lines in the eight diagonal trigrams in each diagonal half of the 8×8 array). Equivalently, 64 = 8 + 56;
2. 24 = 8×3 (e.g., the eight diagonal trigrams);
3. 168 = 84×2 (e.g., the 84 lines & 84 broken lines in the 56 off-diagonal trigrams in each diagonal half of the table of 64 hexagrams;
4. 168 = 56×3 (e.g., each diagonal half of the table has 56 off-diagonal trigrams).
Let us now see whether these patterns manifest in the permutations of the members of a tetractys. Until we establish all these patterns in a holistic system, a sceptic can always argue that it is coincidence that there are 64 permutations of objects other than the central one.
Table 5 lists the 16 permutations of two objects other than the central one chosen from the three rows of the tetractys:
Table 5.16 permutations of two non-central objects.
Combination
Mirror-image
2nd row
BC
CB
3rd row
DF
FD
4th row
GH
HG
GI
IG
GJ
JG
HI
IH
HJ
JH
IJ
JI
They consist of eight basic combinations of two objects (two from the second & third rows, six from the fourth row) and their permutations. It is tempting to identify either set as the eight belonging to the 64 permutations listed in (1) above. However, this is incorrect for the following reason: every one of these permutations has its reverse, or mirror-image, In the case of the 64 trigrams in each half of the table of hexagrams, the 56 off-diagonal trigrams are seven copies of the basic set of eight trigrams. The latter comprises two sets of four trigrams. Each pair consists of one with m Yang lines and (3−m) Yin lines and the other with (3−m) Yang lines and m Yin lines, i.e., they are polar opposites of each other. This means that the 24 lines & broken lines in the eight trigrams comprise 12 Yang lines and 12 Yin lines. Their balance of Yang & Yin lines means that the 56 off-diagonal trigrams consist of 28 trigrams and their polar opposites with Yang & Yin lines interchanged. The counterpart in the 64 permutations of the balance of lines & broken lines in all the 64 trigrams is the fact that every permutation has its reverse, or mirror-image. The only possible choice of eight permutations corresponding to the basic set of eight trigrams that respects this symmetry are the four permutations in the second and third rows (two combinations and their mirror-images) and four permutations in the fourth row consisting of two combinations and their mirror-images. This reproduces the 4:4 division displayed by the eight trigrams. The eight basic combinations of two objects cannot be the right choice because they do not include their own permutations, which would mean, if chosen, that they would leave 56 permutations that did not consist of 28 permutations and their mirror-images. The question now is: which two combinations of objects in the fourth row and their mirror-images make up the eight permutations? There are four combinations that mix corner objects G & J with H & I and two combinations that pair either corners with corners or non-corners with non-corners, namely, GJ & HI. The six combinations naturally divide into a subset of two and a subset of four. It indicates that the eight permutations of two objects consist of the following two sets of four, one the mirror-image of the other:
BC
CB
DF
FD
GJ
JG
HI
IH
This choice is the correct one because the remaining 56 permutations (eight permutations of two objects, 24 permutations of three objects & 24 permutations of four objects) divide into 28 permutations and their mirror-images. A similar analysis and conclusion apply to each orientation of the tetractys. The 192 permutations consist of (8×3=24) permutations of two objects (this explains pattern 2) and (56×3=168) permutations of either two, three or four objects selected from the fourth row (this explains pattern 4), both properties explaining pattern 1. As every permutation has its mirror-image, the 168 permutations consist of 84 permutations and their 84 mirror-images. This explains pattern 3.
Table 6. The universal, holistic patterns in the tetractys and in various sacred geometries.
Holistic
patternTetractys
7 separate polygons
64 hexagrams
Sri Yantra
Disdyakis triacontahedron
384 = 192 + 192
(192+192=384) permutations of objects in (3+3) orientations of tetractys;
384 points, lines & triangles surround the centres of the (7+7) separate Type A polygons;
384 lines/broken lines;
192 lines/broken lines in each diagonal half;
384 yods (192 in each half of the Sri Yantra) surround the 3 corners & centre of its central triangle when its 43 triangles are tetractyses;
384 geometrical elements surrounding its axis consist of 192 elements in each half of the polyhedron & its central 12-gon;
192 = 24 + 168
24 permutations of 2 objects selected from rows of tetractys & 168 permutations of 2, 3 & 4 objects in 4th row;
192 geometrical elements surrounding centres of each set of 7 polygons comprise 24 elements in hexagon & 168 elements in other 6 polygons;
Each diagonal half has 24 lines/broken lines in 8 trigrams & 168 lines/broken lines in 56 off-diagonal trigrams;
192 yods comprise 24 hexagonal yods either at centres of 21 tetractyses or in half of central tetractys and 168 yods lining 21 tetractyses;
192 geometrical elements in each half comprise 24 elements in half of 12-gon and 168 elements on either side of it;
192 = 64×3
192 permutations of non-central objects (64 per orientation);
7 polygons have 192 geometrical elements in 64 sets of 3;
64 trigrams in each diagonal half have 192 lines/broken lines;
Each half of Sri Yantra contains a central triplet of hexagonal yods, 42 triplets of hexagonal yods & 21 triplets of yods (2 corners & centre of tetractys);
192 geometrical elements comprise 64 sets of 3 elements;
64 = 8 + 56
64 permutations = 8 permutations of 2 objects + 56 permutations of 2, 3 & 4 objects in 4th row;
Hexagon has 8 geometrical elements in 2 diametrically opposite sectors repeated 3 times. Other 6 polygons have 56 sets of 3 elements.
8 diagonal trigrams & 56 off-diagonal trigrams in 64 trigrams making up each diagonal half;
Each half contains 64 triplets of yods comprising a triplet of hexagonal yods in the central tetractys, 42 triplets of hexagonal yods & 21 triplets of corners/centres of tetractyses. The 21 centres form 7 triplets;
64 triplets of geometrical elements surrounding axis in each half comprise 56 triplets of elements on either side of 12-gon, which has 8 sets of 3 elements;
24 = 8×3
24 permutations of 2 objects, 8 per orientation;
The hexagon has 3 sets of 2 sectors, each sector having 4 geometrical elements. The hexagon has 3 sets of 8 elements, i.e., 8 sets of 3 elements;
8 diagonal trigrams have 24 lines/broken lines;
8 triplets of yods in each half of the Sri Yantra consist of central triplet & 7 triplets of hexagonal yods at centres of (14+7) tetractyses;
24 geometrical elements in half of central 12-gon surrounding its centre consist of 2 similar sets of 3 types of sectors, each set with 4 elements, i.e., 8 sets of 3 elements;
24 = 12 + 12
24 permutations = 12 permutations + 12 mirror-images;
Each of the 12 geometrical elements in one half of the hexagon has its counterpart in the other half;
12 lines & 12 broken lines in 24 lines/broken lines of 8 diagonal trigrams;
12 yods comprise central triplet of hexagonal yods & centres of 9 tetractyses in 1st 2 layers; 12 yods are centres of 12 tetractys in 3rd & 4th layers;
These 24 geometrical elements consist of 2 similar sets of 12 elements;
168 = 56×3
168 permutations of 2, 3 & 4 non-central objects, 56 per orientation;
Triangle has 4 sets of 3 elements, square & octagon have 16 sets of 3, pentagon & decagon have 20 sets of 3 and dodecagon has 16 sets of 3; the 6 polygons have 56 sets of 3.
168 lines/broken lines in 56 off-diagonal trigrams;
168 yods line the 63 sides of the 21 tetractyses in each half as 56 triplets of yods;
168 geometrical elements surrounding axis on either side of central 12-gon consist of 3 sets of 8 vertices and 3 sets of 48 edges & triangles, i.e., 56 sets of 3 geometrical elements;
168 = 84 + 84
168 permutations = 84 permutations + 84 mirror-images.
84 geometrical elements surround the centres of the triangle, octagon & decagon; 84 geometrical elements surround the centres of the square, pentagon & dodecagon.
84 lines & 84 broken lines in 168 lines/broken lines in 56 off-diagonal trigrams.
168 yods lining 63 sides = 84 corners or hexagonal yods on bases of tetractyses + 84 hexagonal yods on their other sides.
84 sides and 84 vertices & triangles surround axis in each half of polyhedron.
Table 6 compares how the various patterns in a holistic system are realised in the tetractys and in four sacred geometries. Article 46 describes the 64×3 pattern also in the context of the 64 codons of mRNA and the 64 anticodons of tRNA, the intervals between the notes in the seven diatonic musical and the symmetries of the Klein quartic embedded on a 3-torus. In particular, see Table 7 in that article.
The counterpart in sacred geometries of the tetractys of objects and the tetractys of its ‘mirror-images’ are their two halves, one the mirror image of the other. The (64+64) permutations of their (10+10) members manifest in DNA as the 64 codons of mRNA and the 64 anticodons of tRNA, in music as the 64 triplets of rising & falling intervals between the notes of the seven diatonic scales and in the Klein quartic as the 64 triplets of yods that line the 56 tetractyses tiling both the 3-torus, onto which its 168 automorphisms can be mapped, and the version of it created by turning it inside-out, onto which its 168 anti-automorphisms can be mapped. The counterparts of the three possible orientations of each tetractys are their three-fold yod or geometrical compositions, which have been analysed in many earlier articles by the author. In the case of the Klein quartic, the 168 sheets of its Riemann surface join at its three branch points into 84 pairs, 24 groups of 7 and 56 groups of 3 (see here, p. 19). In the case of the diatonic 8-note scales, their notes form 56 triplets of intervals other than those between the tonic and themselves, each triplet consisting of an interval n paired with its inversion 2/n and an unpaired interval.
In conclusion, hidden within the tetractys — the "Rosetta Stone" of sacred geometries that deciphers the information encoded in them — is the potential, in terms of all possible permutations of its 10 members, to generate structural parameters of the outer & inner Trees of Life, such as 192, 222 & 232. The numbers of objects in these permutations are the numbers of yods surrounding the centres of the seven enfolded polygons in each half of the inner Tree of Life.
<< Previous 1... 64 65 [66] 67 68 ...81 Next >>