#58 The five Platonic solids embody the holistic parameter 384

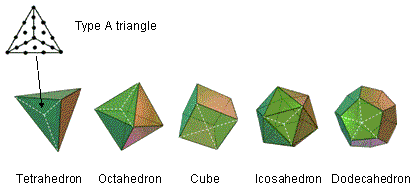
Suppose that the faces of the five Platonic solids are regarded as Type B regular polygons, i.e., their sectors are regarded as Type A triangles composed of three tetractyses. If a Platonic solid has C vertices, E edges and F faces, each an n-sided, regular polygon, then:

Number of sectors in the F faces = nF. Therefore, number of tetractyses in the F faces = 3nF.

Number of corners of the 3nF tetractyses making up the F faces ≡ V = C + F + nF = 2 + E + nF, using Euler's polyhedron formula:

C − E + F = 2.

The number "2" in this expression for the number of corners can be interpreted as the two vertices on the axis passing through the centre of the Platonic solid. Hence, (E+nF) corners surround its axis.

Number of hexagonal yods on the sides of the E edges = 2E.

Number of hexagonal yods on the nF sides of the nF sectors of the F faces = 2nF.

Number of hexagonal yods on the 3nF sides of the 3nF tetractyses inside the nF sectors = 6nF.

Number of hexagonal yods at centres of the 3nF tetractyses ≡ h = 3nF.

Total number of hexagonal yods ≡ H = 2E + 11nF.

Total number of yods in F faces ≡ N = V + H = 2 + E + nF + 2E + 11nF = 2 + 3E + 12nF. Hence, (3E+12nF) yods surround the axis.

Number of yods lining sides of the 3nF tetractyses ≡ B = N − h = 2 + 3E + 9nF. Hence, (3E+9nF) yods surround the axis, lining sides of tetractyses.

For the five Platonic solids, ∑E = 90 and ∑nF = 180. Therefore:

• the number of corners of the (3×180=540) tetractyses in the faces of the five Platonic solids = ∑(2+E+nF) = 5×2 + 90 + 180 = 280. The number 280 of Sandalphon, the Archangel of Malkuth, is the number of points making up the faces of the five Platonic solids. Of these, 40 points are vertices that surround their axes, leaving 240 points that are either on their axes or not vertices; 
• the number of hexagonal yods = ∑(2E+11nF) = 2×90 + 11×180 = 2160 = 10×216, where 216 is the number value of Geburah; 
• the number of yods = 280 + 2160 = 2440; 
• the number of yods lining sides of the 540 tetractyses = ∑(2+3E+9nF) = 5×2 + 3×90 + 9×180 = 1900. As 1900 = 38×50, this is the sum of the number 50 of ELOHIM, Godname of Binah, assigned to the 38 yods in two separate Type A triangles. In other words, assigning 50 to each of the 19 yods in one of the sectors of the 25 faces making up either upper or lower halves of the five Platonic solids generates the number (950) of yods in those five halves! 950 = 95×10, where 95 is the number value of Madim, the Mundane Chakra of Geburah, which is the fifth Sephirah from the top of the Tree of Life.

As well as the 2440 yods in their 50 faces, the axis of each Platonic solid has four hexagonal yods when their interiors are constructed from tetractyses (this construction will not be considered here). Therefore, (2440 + 5×4 = 2460 = 246×10) yods in their faces and axes surround their centres. 246 is the number value of Gabriel, the Archangel of Yesod. The number of yods in their five axes and on sides of tetractyses surrounding their centres = 1900 + 5×4 = 1920. On average, the centre of a Platonic solid is surrounded by (1920/5=384) yods either in axes or lining tetractyses in its faces, 192 yods being in each half. Including the centre, there are, on average, 385 yods either in the axis of a Platonic solid or lining tetractyses in its faces, where

This is a remarkable demonstration of how the Decad (10) expresses the number of yods needed on average to generate the axis and sides of the tetractyses in the faces of a Platonic solid. This number includes the average number of 10 vertices and the average number of 10 centres of faces.

On average, there are (280/5=56) corners of the (540/5=108) tetractyses in the faces of the five Platonic solids. They comprise eight vertices surrounding the axis and 48 corners that are either on the axis or not vertices, 24 such corners being in each half. Hence, half a Platonic solid (including its half-axis) has, on average, 192 yods on sides of tetractyses that consist of a set of 24 corners and a set of 168 corners & hexagonal yods (four vertices, two hexagonal yods on its half-axis & 162 hexagonal yods). The 384 yods that, on average, are either in the axis or line tetractyses in the faces of a Platonic solid display the following divisions:

384 = 192 + 192,

192 = 24 + 168,

384 = 48 + 336,

336 = 168 + 168.

These divisions are characteristic of sacred geometries (see here). For example, the (7+7) separate polygons have 384 geometrical elements surrounding their 14 centres, and the 64 hexagrams familiar to students of I Ching consist of 384 lines & broken lines. These and other examples of the embodiment of this parameter in sacred geometries are discussed next. Of course, there exists no polyhedron (regular or not) that has the properties of this hypothetical, average Platonic solid. But that is not the point. The crucial remarkable conclusion is that it displays the divisions that are characteristic of holistic systems, indicating that the five Platonic solids are holistic as well. Since the time of the ancient Greeks, it has always been thought that the regular polyhedra have an archetypal character. This result mathematically proves this ancient claim by constructing the five Platonic solids from the tetractys — the representation of the 10-fold nature of Divine Unity.

<< Previous    1...   56  57  [58]  59  60  ...81    Next >>

Home