| << Previous 1... 57 58 [59] 60 61 ...81 Next >> |
#59 How sacred geometries embody the holistic parameter 384
| Click here to see a high-resolution PDF version of this picture. |
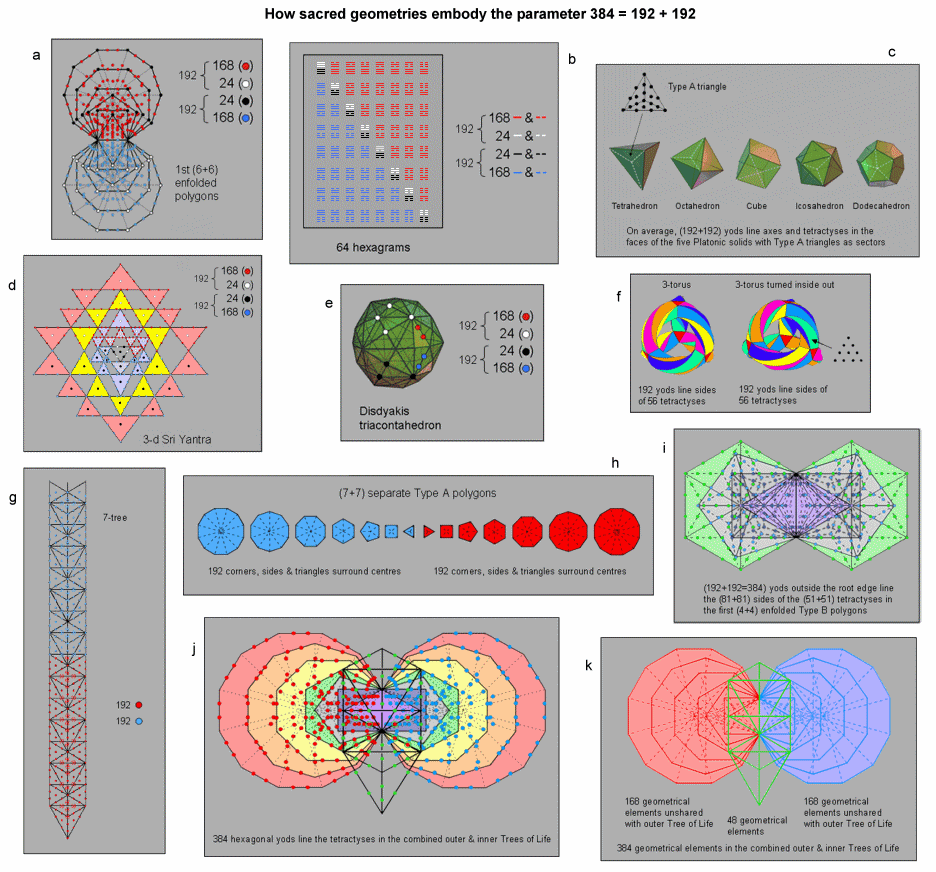
We shall show how eleven examples of sacred geometry embody the parameter 384 that is characteristic of holistic systems (as discussed here), as well as its division:
384 = 192 + 192,
where
192 = 24 + 168.
Some of these examples are also discussed in #36.
a) The first (6+6) enfolded polygons of the inner Tree of Life have 386 yods when their 70 sectors are turned into tetractyses. There are 192 yods other than the endpoints of the shared root edge that are associated with each set of six enfolded polygons. They contain 24 (white or black) corners and 168 (red or blue) hexagonal yods. See here. Alternatively, the first (6+6) enfolded polygons have 384 yods that are intrinsic to them in the sense that none are shared with polygons enfolded in the next higher Tree (see here).
b) The 64 hexagrams in the ancient Chinese system of divination called "I Ching" are composed of 384 lines & broken lines. Each diagonal half of the 8×8 array of hexagrams comprises 192 such lines & broken lines. There are 24 white lines & broken lines in the eight upper trigrams in the eight diagonal hexagrams and 168 red lines & broken lines in the 28 off-diagonal hexagrams in the upper half of the array. The eight lower trigrams in the diagonal hexagrams are composed of 24 black lines & broken lines. The 28 off-diagonal hexagrams in the lower half contain 168 blue lines & broken lines. See here for comparison with the Sri Yantra shown in (d).
c) When the faces of the five Platonic solids are divided into their 180 sectors and each sector turned into a Type A triangle containing 19 yods, there are on average 384 yods that surround their centres and which line either their axes or the tetractyses in their faces, apart from vertices in the latter case. See here.
d) When the 43 triangles of the 3-dimensional Sri Yantra are tetractyses, there are 336 yods lining the 42 tetractyses that surround the central one. 168 red yods line the 63 sides of the 21 tetractyses in one half of the Sri Yantra and 168 blue yods line the sides of the 21 tetractyses in its other half. Two triangular arrays of three white or black hexagonal yods intersect each other, forming a Star of David in the central triangle. One array is associated with the 21 white hexagonal yods at the centres of the tetractyses in the upper half and the other array is associated with the 21 black hexagonal yods at the centres of the tetractyses in the lower half. The 384 yods in the 3-dimensional Sri Yantra comprise 48 white or black hexagonal yods and 336 red or blue yods. See here.
e) The disdyakis triacontahedron is the polyhedral form of the inner Tree of Life (see
Sacred geometry/Polyhedral Tree of
Life). It has 62 vertices, 180 edges and 120 triangular faces. When
the latter are tetractyses, (180×2 + 62 = 422) yods line its edges. 420 yods (including 60
vertices) surround an axis passing through two diametrically opposite vertices. When the latter are A vertices
(defined here), there are 12 vertices and 12 edges in its equatorial plane
perpendicular to this axis. They comprise 36 yods. Therefore,
(420−36=384) yods surround the axis that lie above and below this plane. The 192 yods in each
half of the polyhedron comprise 24 vertices and 168 hexagonal yods that line 84 edges. See
also here. It was shown in #15 that, when their faces are constructed from tetractyses,
the 29 polyhedra that can be fitted to the vertices of the disdyakis triacontahedron contain 3840 hexagonal yods
(see diagram opposite).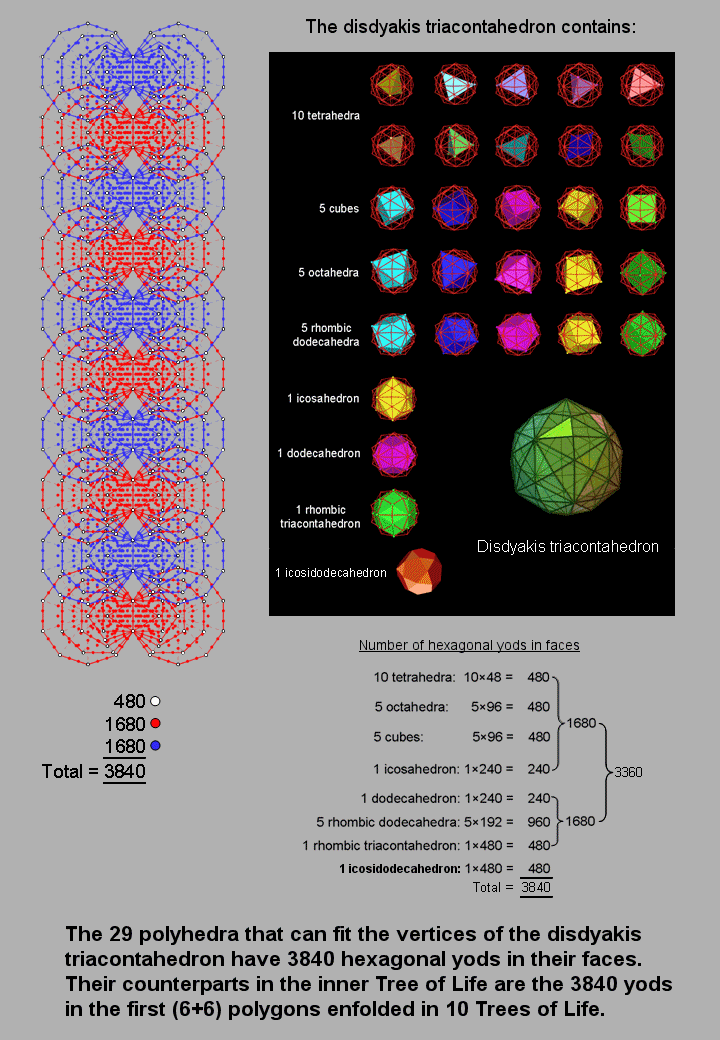 
1680 hexagonal yods belong to the 21 Platonic solids, 1680 hexagonal
yods belong to the dodecahedron, the five rhombic dodecahedra and the rhombic triacontahedron, and 480
hexagonal yods belong to the icosidodecahedron. The 1920 hexagonal yods in the faces of the polyhedra in each
half of the disdyakis triacontahedron consist of 240 hexagonal yods belonging to the icosidodecahedron and
1680 hexagonal yods making up the other 28 polyhedra. Amazingly, the 29 polyhedra that can be fitted to the
vertices of the disdyakis triacontahedron reproduce through their hexagonal yods (apart from the Pythagorean
factor of 10) the same 24:168 division that is displayed in its faces.
The counterparts in the inner Tree of Life of the 3840 hexagonal yods needed to construct the faces of the 29 polyhedra are the 3840 intrinsic yods that make up the the first (6+6) polygons enfolded in 10 overlapping Trees of Life when their sectors are tetractyses. They comprise 480 corners intrinsic to the polygons enfolded in these Trees and 3360 other yods. For the sake of clarity, the diagram opposite depicts two sets of 1680 yods coloured red and blue in alternate Trees, but they can, alternatively, be regarded as 1680 red yods distributed in a set of 60 polygons enfolded on one side and a set of 1680 blue yods in the set of 60 polygons enfolded on the other side. Indeed, this arrangement is more consistent with the interpretation of the 3360 yods as circular turns of the ten helical whorls of the UPA/superstring, for what is being represented here is not the 3360 turns of just two whorls but, rather, one revolution of all ten whorls (hence the ten overlapping Trees, each denoting a whorl), which means that the 1680 yods other than polygonal corners on either side denote not ten half-revolutions of one whorl but, instead, the 1680 turns in a half-revolution of all ten whorls. This view is also consistent with the 240 corners of each set of 60 polygons denoting plane wave components of the 24 circularly polarized waves running around each whorl and associated with E8 gauge charges. This is because the 24 pairs of corners, one the mirror image of the other, that are intrinsic to the first (6+6) polygons enfolded in each Tree would denote the 24 pairs of plane wave components, repeated in each whorl, of a circularly polarized oscillation that are out of phase with each other by 90°.
f) The 168 automorphisms of an equation known to mathematicians as the "Klein quartic" can be mapped onto the 3-torus (see Article 15 & Article 43. The {3,7} tessellation of its hyperbolic surface requires 56 triangles. When the latter are turned into tetractyses, 192 yods line their 84 sides. 24 yods are corners and 168 are hexagonal yods. The 168 anti-automorphisms of the Klein quartic can be mapped onto the turned inside-out version of the 3-torus. 192 yods line its 56 tetractyses. Both tori have 384 yods lining their 112 tetractyses. They comprise 48 corners of tetractyses and 336 hexagonal yods. The primary division: 384 = 192 + 192 manifests as the yod populations of the 3-torus and its mirror reflection when they are tessellated with tetractyses. See here.
g) There are 380 yods in the 7-tree mapping the physical plane up to its apex when its 91 triangles are turned into tetractyses (see proof here). Outside it up to the level of this apex are two yods belonging to the eighth Tree on each side of the central Pillar of Equilibrium. Therefore, there are 384 yods up to the top of the 7-tree. They comprise 192 red yods below the Path connecting Chesed and Geburah of the fourth Tree and 192 blue yods above this line. Alternatively, there are 48 yods up to Chesed of the first Tree and 336 yods above it. See further discussion here.
h) The inner Tree of Life consists of two sets of seven regular polygons, one the mirror image of the other. The centres of the 14 separate polygons are surrounded by 384 points, lines & triangles. The 192 geometrical elements surrounding the centres of each set of polygons comprise the 24 elements in the hexagon and the 168 elements of the six other polygons. See here.
i) When they are Type B, the first (4+4) enfolded polygons have 384 yods outside the shared root edge that line sides of tetractyses. 192 such yods line the 81 sides of the 51 tetractyses in each set of the first four polygons. See here.
j) When the outer Tree of Life constructed from tetractyses is superimposed on the (7+7) enfolded polygons of the inner Tree of Life constructed from tetractyses, there are 384 hexagonal yods that line sides of their tetractyses. See here.
k) The combined outer and inner Trees of Life are composed of 384 geometrical elements. The former (coloured green) has 48 elements, and each set of seven enfolded polygons (coloured red and blue) has 168 geometrical elements that are unshared with it. See here.
That the number 192 is a defining parameter of holistic systems is demonstrated also by the 10-tree, as now explained. The 91 Trees of Life of CTOL with 550 SLs can be thought of as a Tree of Life whose 10 Sephiroth are each represented by 10 overlapping Trees, the tenth Tree for each Sephirah being the first Tree for the next one, so that the 10-tree represents Malkuth, the last Sephirah, as illustrated by its Godname ADONAI, whose number value 65 is the number of SLs in the last 10 Trees of CTOL. When its 127 triangles are Type A, their 381 sectors have 192 corners and 550 sides (see here).
Conclusion
The fundamental 48:336 division displayed by these sacred geometries manifests in the subquark
state of the E8×E8 heterotic superstring as the 48 plane wave
components of the 24 circularly polarized waves that carry E8 gauge charges spread along each of
its ten whorls and as the 336 oscillations made by these waves as they travel once around the axis of the subquark.
In all cases, the number 336 is the number of things that express the shape or
form of an object defined fundamentally by the number 48, which always refers to
higher-order entities existing as complementary pairs (usually an entity and its mirror
image). The 48:336 division of the parameter 384 embodied in
sacred geometries manifests also in the seven musical scales, as will be discussed next.
