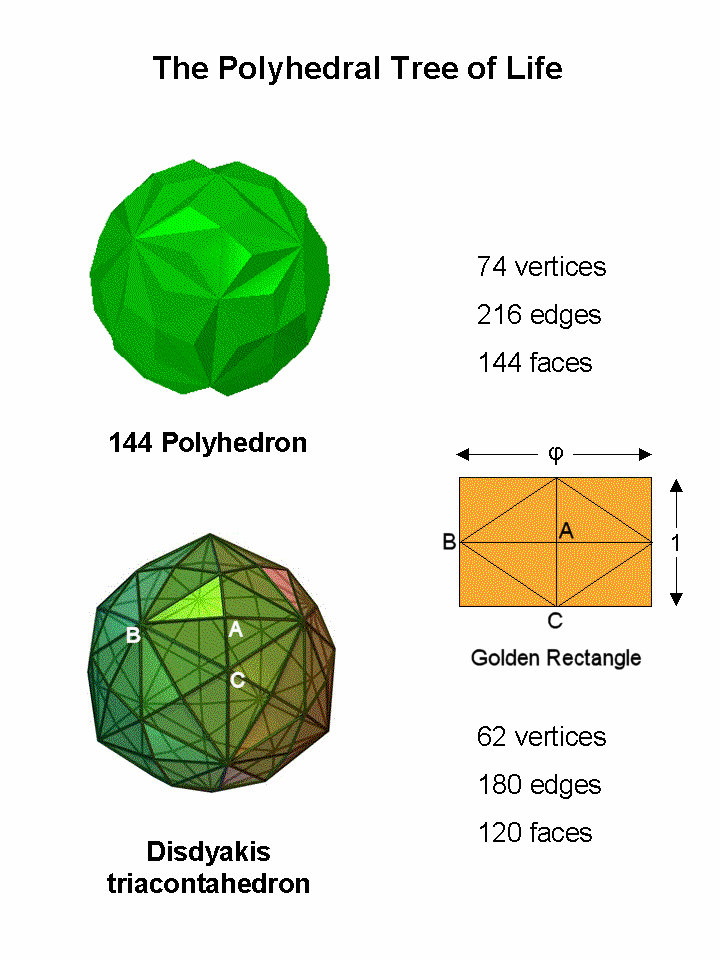
The disdyakis triacontahedron and the 144 Polyhedron are the two polyhedra whose respective numbers of faces — 120 & 144 — are symbolized by the 120 yods lining the sides of the seven enfolded polygons of the Tree of Life and by the 144 yods inside them. The 144 Polyhedron has 74 vertices (26 belonging to its underlying disdyakis dodecahedron), 216 edges & 144 triangular faces. The disdyakis triacontahedron has 62 vertices, 180 edges & 120 triangular faces. It is created by sticking four-faced pyramids onto the 30 faces of another Catalan solid called the "rhombic triacontahedron." The faces of the latter are Golden Rhombi, that is, rhombi that can be enclosed by Golden Rectangles, whose adjacent sides have lengths in the proportion of the Golden Ratio Φ = (1+√5)/2 = 1.618.... The peaks of the rhombic pyramids will be called "A vertices. The vertices at the ends of the longer diagonal of the Golden Rectangle will be called "B vertices" and the ends of the shorter diagonals will be called "C vertices." The 62 vertices of the disdyakis triacontahedron comprise 30 A vertices, 12 B vertices & 20 C vertices. 

 

<< Previous    1...   2  3  [4]  5  6  ...15    Next >>

Home