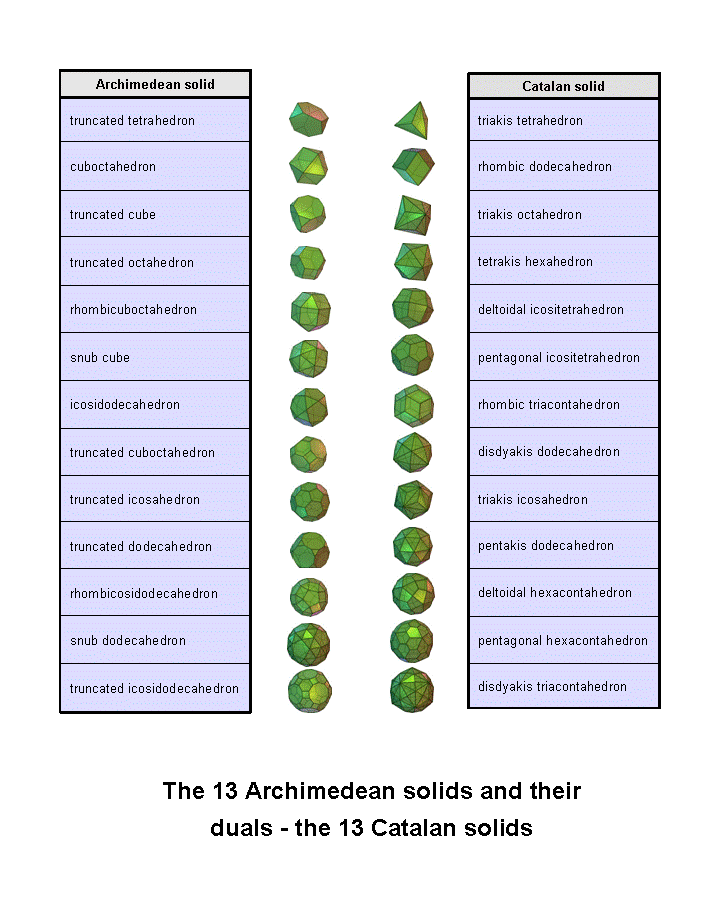
There are 13 polyhedra with two or more regular polygons as their faces. Called the "Archimedean solids," each has a dual called a "Catalan solid," in which vertices are replaced by faces and faces become vertices. Although there is an Archimedean solid (truncated icosidodecahedron) with 120 vertices, there are no Archimedean or Catalan solids with 144 vertices. This means that the 264 yods in the seven enfolded polygons cannot symbolize vertices of one or more polyhedra. Although there is a Catalan solid with 120 faces, there are no Archimedean or Catalan solids with 144 faces. The disdyakis triacontahedron is this Catalan solid with the most faces. However, the Catalan solid called the "disdyakis dodecahedron" has 48 triangular faces. Sticking tetrahedra on its faces creates a required polyhedron with 144 faces. Adding square pyramids with four faces to an Archimedean or a Catalan solid cannot create such a polyhedron because there is none that has 36 faces. Only one member of the 26 Archimedean & Catalan solids can therefore generate a polyhedron with 144 faces. The disdyakis dodecahedron has 26 vertices, 72 edges & 48 faces. Adding tetrahedra to the latter creates a polyhedron with (26+48=74) vertices, (72 + 3×48 = 216) edges and (48×3=144) triangular faces. This will be called the "144 Polyhedron."

 

<< Previous    1  2  [3]  4  5  ...15    Next >>

Home