| << Previous 1... 11 12 13 14 [15] Next >> |
How the Polyhedral Tree of Life is isomorphic to its polygonal counterpart

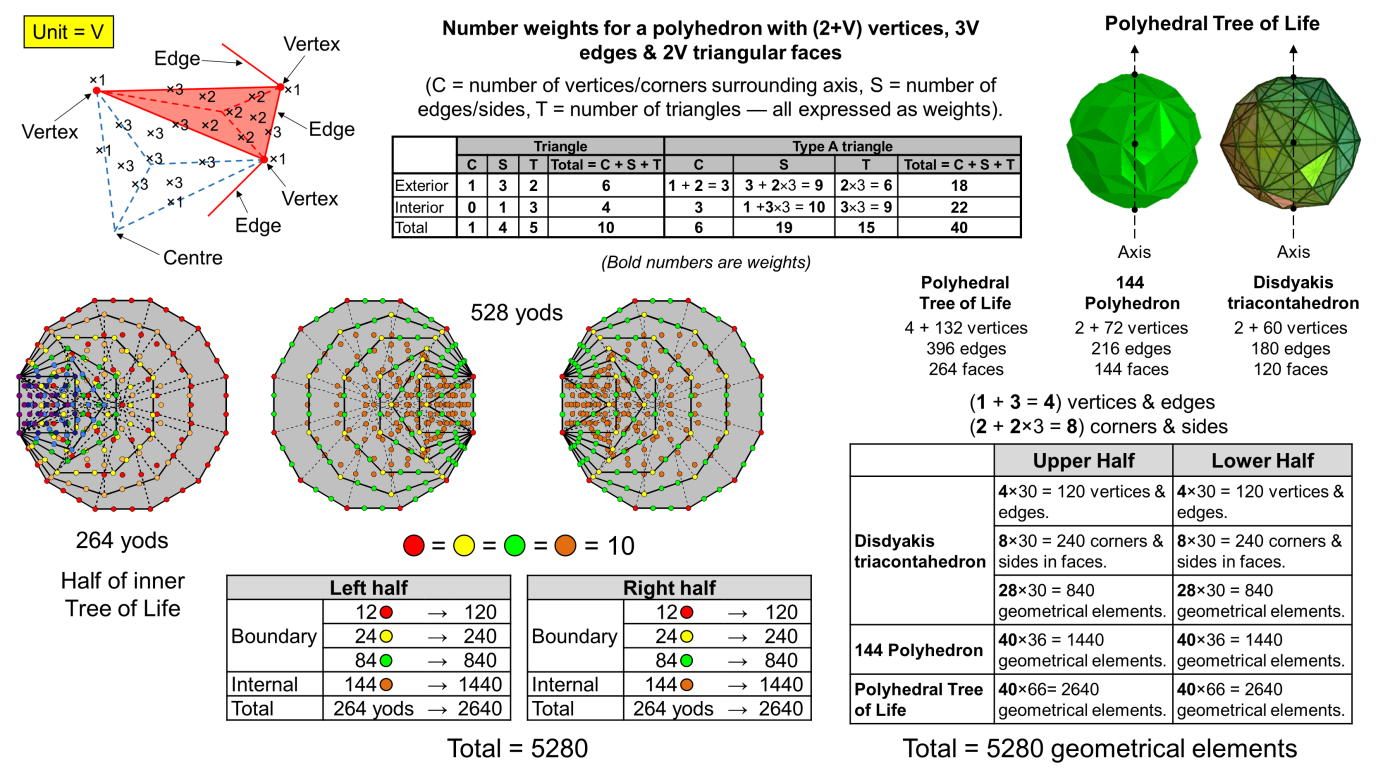
We have already seen that the 120 faces of the disdyakis triacontahedron and the 144 faces of the 144 Polyhedron are symbolised by, respectively, the 120 yods lining the seven enfolded polygons of the inner Tree of Life and the 144 yods inside their boundaries. We shall now show that this 5:6 division is just part of the complete isomorphism between the polygonal and polyhedral versions of the Tree of Life.
In order to simplify calculation, the notion of geometrical "weights" will be introduced. What makes this helpful is the fact that, although very different in their morphology, both the constituents of the Polyhedral Tree of Life exhibit the property that the ratio
number of vertices surrounding an axis:number of edges:number of faces
is 1:3:2. In other words, the ratio of the number of vertices = 60/72 = 5/6, the ratio of the number of edges = 180/216 = 5/6 and the ratio of the number of faces = 120/144 = 5/6. It means that all seven combinations of corners, sides and triangles are also in the ratio of 5/6. Suppose that a polyhedron has (2+V) vertices, 3V edges and 2V faces. This is consistent with Euler's polyhedral formula:
C − E + F = 2
obeyed by a polyhedron with C vertices, E edges & F faces because 2 + V − 3V + 2V = 2. Of course, not all polyhedra possess this 1:3:2 scaling property, but the 144 Polyhedron and the disdyakis triacontahedron do, and this makes calculation of their geometrical composition easier than for the majority of polyhedra, for which the various proportions of vertices, edges & faces may be fractions, not integers.
Once we know the values of C, E & F for a polyhedron, we can calculate the numbers of points, lines & triangles making up its exterior and interior when all triangles are basic triangles, Type A triangles, Type B triangles, etc. But these numbers can become large, and calculation can be made simpler by dropping the common factor of V, considering it only when we want to know what the actual magnitude of a number is, and working, instead, with its equivalent weight. So we work with the weight 1 denoting V vertices, the weight 2 denoting 2V faces, the weight 3 denoting the 3V edges, as well as all their combinations in the exterior and interior of the polyhedron. All weights will be written in bold in order to differentiate them from purely multiplicative factors that arise from how many times the type of geometrical element appears in a representative face or internal triangle. For example, the centre of an internal Type A triangle will have a weight of 3 because every edge is the side of an internal triangle and occurs 3V times, whilst the side of a sector of a face that is (let us say) a Type A triangle will have a weight of 2×3 = 6 because three sides of sectors are within every face, 2V of which are in the polyhedron. Gematria number values of Sephiroth, Godnames, etc are written throughout this website in bold. This practice will be dropped in the remainder of this section in order to avoid any confusion with number weights.
The number weights for a polyhedron with (2+V) vertices, 3V edges and 2V faces are tabulated in the diagram shown above. Any entry must be multiplied by either 60 to give actual numbers for the disdyakis triacontahedron or by 72 to give numbers for the 144 Polyhedron. For both polyhedra, an entry should be multiplied by (60+72=132). For example, the weight for the total number of geometrical elements surrounding the axis of a polyhedron with simple triangles as its faces and interior triangles is 10, so that the number of such elements in the Polyhedral Tree of Life = 10×132 = 1320. As the axes of the two polyhedra comprise four vertices, two centres and four sides of internal triangles, the total number of geometrical elements in the Polyhedral Tree of Life = 1320 + 10 = 1330
|
12 |
||||
|
|
32 |
52 | ||
| = |
72 |
92 |
112 |
|
| 132 | 152 | 172 | 192 . |
(see also discussion of this number in the previous page). This beautiful, mathematical property confirms its archetypal status. The integers 1, 2, 3 & 4 symbolised by the four rows of the Pythagorean tetractys are the number weights for, respectively, the number of corners, the number of triangles in the faces, the number of sides in faces (alternatively, the number of internal triangles) and the number of internal sides and triangles (alternatively, the number of sides). The 144 Polyhedron has (10×72=720) geometrical elements surrounding its axis. This is the number of yods that surround the centre of the 10-cornered decagon with 2nd-order tetractyses as its sectors:
| 720 = | 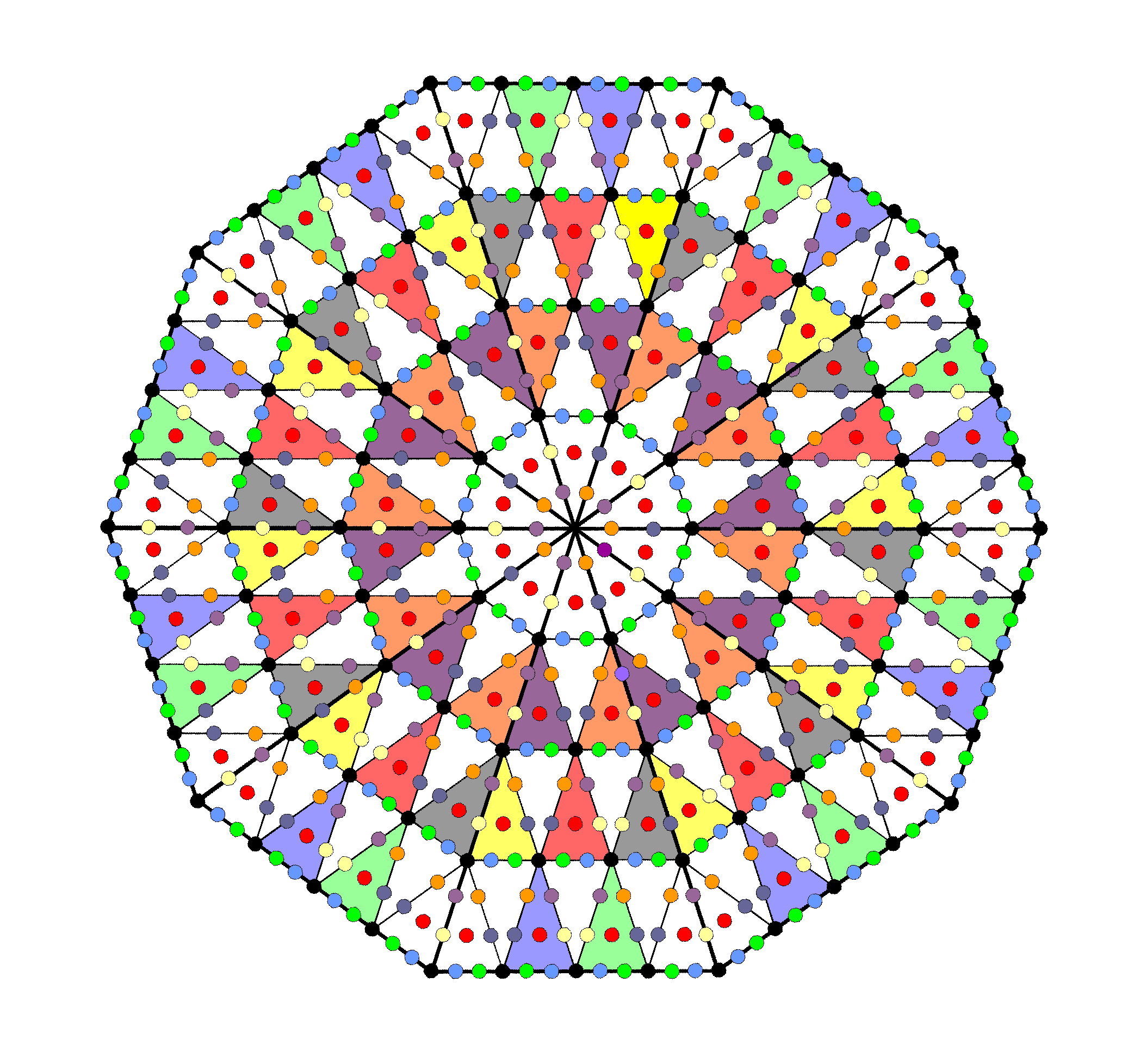 |
The Polyhedral Tree of Life has (4×132=528) sides of (5×132=660) triangles. Alternatively, it has 528 vertices & edges surrounding the axes of the two polyhedra. There are 330 triangles with 264 sides in each half of the pair of polyhedra. This corresponds to the 264 yods in each half of the inner Tree of Life made up of seven enfolded, Type A polygons (see diagram).
When all faces and internal triangles are Type A, the number weight for the total number of geometrical elements in a polyhedron with (2+V) vertices, 3V edges & 2V faces is 40, i.e., it increases by a factor of four. This means that the total number of geometrical elements surrounding the axes of the two polyhedra = 40×132 = 5280 = 528×10. This number is what is generated when the number 10 expressing the ten Sephiroth of the Tree of Life and the ten yods of the tetractys is assigned to every one of the 528 yods in the two separate halves of the inner Tree of Life. The appropriateness of naming the dots of a tetractys as yods is very apparent, for Hebrew gematria assigns the number 10 to this letter of the Hebrew alphabet. The number 5280 is the number of feet in a mile, whilst 660 (the number of corners other than vertices) is the number of feet in one furlong. The distance of 528 ft represents 1/10th of a mile. It is 176 yards. It is remarkable that the number of geometrical elements in the seven enfolded Type A polygons with 264 yods is 176. The ratio:
number of yods in 7 enfolded polygons/number of their geometrical elements = 264/176 = 3/2
holds true for the yod and geometrical populations of the faces of the two polyhedra, as now shown. The number of edges = 3, so that the number of hexagonal yods lining them = 3×2 = 6, whilst the number of hexagonal yods at centres of tetractyses = 2. Therefore, the total number of yods in faces = 1 + 6 + 2 = 9. The number of geometrical elements in faces = 6. Their ratio is 3/2. In the case of Type A triangles, there are 9 sides of 6 triangles with 3 corners in the faces, so that (9×2=18) hexagonal yods line them. The total number of yods in the faces = 3 + 18 + 6 = 27, whilst their total number of geometrical elements = 18. Once again, their ratio is 3/2. This is the tone ratio of the perfect fifth in music, which is the halfway point between the beginning of an octave and its end, being the arithmetic mean of the tone ratios of the tonic (1) and octave (2). Page 7 of Article 65 proves that the ratio of the yod and geometrical populations of the seven enfolded polygons is always 3/2, whether they are Type A, Type B, Type C, etc. Indeed, this is also true for individual m-gons, whatever m is or whatever their type/order. The formulae for the number of yods or geometrical elements that surround the centre of the nth-order m-gon are:
| Number of yods: | 3m(1+3n)/2 |
| Number of geometrical elements: | m(1+3n) |
(see Table 9 on page 5 of Article 65). Their ratio is 3/2, whatever m and n are.
The sum of the seven numbers forming Plato's Lambda is 54 and the sum of the three numbers interpolated to make the Lambda Tetractys is 36 (see here); their ratio is 3/2.
Having established the existence of a parallelism between the global properties of the polygonal and polyhedral versions of the Tree of Life, let us next explore these correspondences in more detail. The 120 yods on the boundaries of each set of seven enfolded polygons consist of their 36 corners and 42 pairs of hexagonal yods. The former comprise the 12 corners of the dodecagon (the last of the seven polygons) and the 24 corners of the first six enfolded polygons. Inside the boundaries of the seven polygons are 144 yods. Weighted with the number 10, they naturally generate the numbers 120, 240, 840 & 1440. Given that the weight for vertices & edges = 1 + 3 = 4 and that the weight for corners & sides of triangles in faces = 2 + 2×3 = 8, the weight for all corners & sides in faces = 4 + 8 = 12, so that the weight for all triangles and internal geometrical elements = 40 − 12 = 28. Surrounding the axis of the disdyakis triacontahedron are 60 vertices (30 in each half). There are (4×30=120) vertices & edge in each half of the polyhedron; they correspond to the number 120 generated by the 12 corners of the dodecagon in each set of seven polygons. There are (8×30=240) corners & sides in the 60 faces in each half of the polyhedron; they correspond to the number 240 generated by the 24 corners of the first six polygons. There are (28×30=840) triangles in faces and geometrical elements in the interior of each half; they correspond to the number 840 generated by the hexagonal yods on the boundaries of each set of seven enfolded polygons. Finally, each half of the 144 Polyhedron has 36 vertices surrounding its axis, so that each half has (40×36=1440) geometrical elements; this compared with the number 1440 generated by the 144 yods inside each set of seven enfolded polygons. Each half of the Polyhedral Tree of Life contains 2640 geometrical elements, which is the number generated when the number 10 is assigned to each of the 264 yods making up each half of the inner Tree of Life. Only two polyhedra with the same scaling ratio of 1:3:2 and with 132 vertices surrounding their axes would embody both the number 1330 discussed earlier and the number 5280. Only one with 60 such vertices would have (12×60=720) corners & sides of sectors in faces and (28×60=1680) triangles & internal geometrical elements — the two numbers that match the 72:168 division of yods on the boundaries of the two sets of seven enfolded polygons. The two polyhedra that comprise the Polyhedral Tree of Life — the 144 Polyhedron and the disdyakis triacontahedron — are unique in having geometrical compositions that are isomorphic to its polygonal counterpart.
As 232 = 529, the number 528 is the sum of the 22 odd integers after 1:
528 = 232 − 1 = 3 + 5 + 7 + ... + 45.
Their arithmetic mean is 24 = 1×2×3×4. Including the 10 geometrical elements that make up the axes of the two polyhedra, the Polyhedral Tree of Life is composed of 5290 geometrical elements, where 5290 = 10×232 = 10 + 30 + 50 + ... + 450. As
172 − 1 = 288 = 3 + 5 + 7 +... + 33,
528 = 288 + 240,
where
240 = (35 + 37) + 39 + 41 + 43 + 45
= 72 + 168,
where 72 is the number of corners in the two separate sets of seven enfolded polygons and 168 is the number of hexagonal yods lining their sides. The first 22 odd integers after 1 add up to generate:
Sacred geometry always exhibits perfect harmony between number and geometry. That is why it is sacred. It expresses the properties of numbers in a way that transcends in scope the power of any human mind to invent. It comes from "outside." The materialist cannot account for its design and beauty — for its awesome intelligence and logical coherence. So he can only ignore it, pretending to everyone that it has no substance. But his disbelief that sacred geometry has in reality (or even can have in principle) any worth is based upon either ideology, ignorance or dishonest denial. It has no rational basis and should fool no one.
The number 528 is sacred because it is the number of yods in the two separate halves of the inner Tree of Life. Because of the isomorphism between the polygonal and polyhedral versions of the inner Tree of Life, this holistic parameter re-appears as either the 528 sides of the triangles making up the 144 Polyhedron and the disdyakis triacontahedron that surround their axes or, equivalently, the number of surrounding vertices & edges. Each of the two pairs of halves of the two polyhedra corresponds to each set of seven enfolded, Type A polygons. The inversion of one pair relative to the other corresponds to one set being the mirror image of the other set.
| << Previous 1... 11 12 13 14 [15] Next >> |