The dodecagon
TYPE A DODECAGON
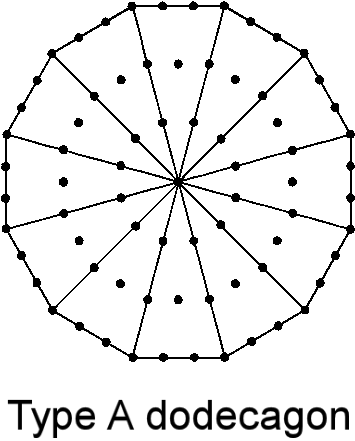
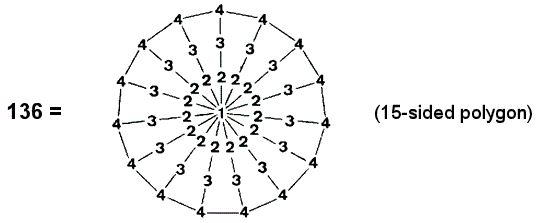
(1) The Type A dodecagon has 73 yods (the 36th odd integer after 1) and so the
tenth regular polygon embodies the number 73 of Chokmah. It has 36 boundary yods
and 36 internal yods surrounding its centre, where 36 is the number value of ELOHA, the
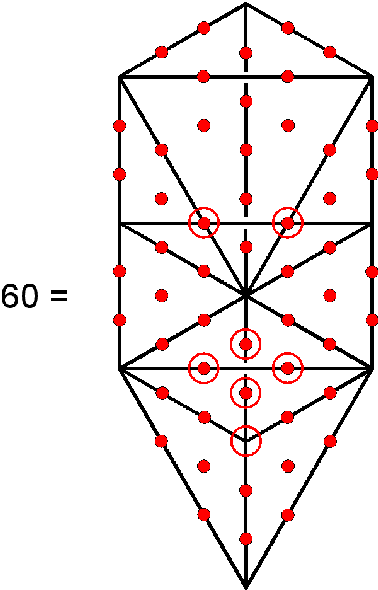
Godname assigned to Geburah. It contains 60 hexagonal yods. This is the number of hexagonal yods in the Tree of
Life when its 16 triangles are tetractyses:
 |
 |
 |
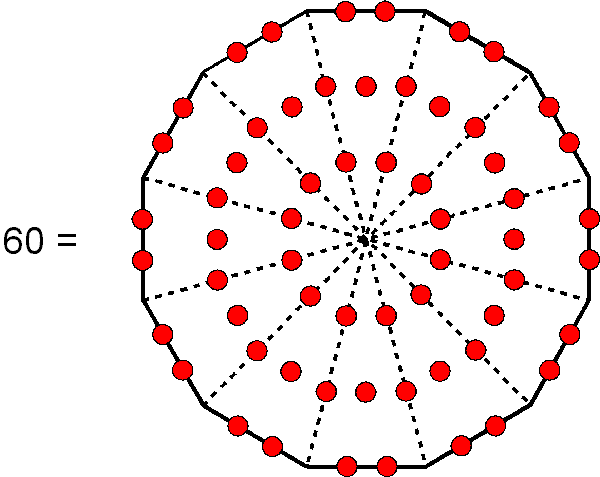
Two separate dodecagons have 146 yods, of which
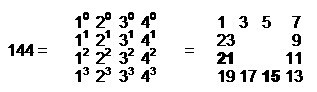
yods surround their centres. This is both the number of boundary yods and the number of internal yods of the seven separate Type A polygons other than their centres:
144 is the 12th Fibonacci number and the only square Fibonacci number apart from 1. Two enfolded dodecagons have 140 yods surrounding their centres, where 140 is the number of both Masloth, the Mundane Chakra of Chokmah, and Malachim, the Order of Angels assigned to Tiphareth. 70 such yods are associated with each dodecagon:
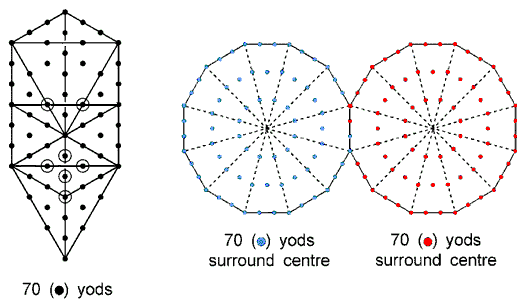
As this is the number of yods in the Tree of Life when all its triangles are tetractyses,
we see that its measure is realized in the dodecagon. No single n-gon can have 70 yods because there is no
integer value of n for which 6n + 1 = 70. Nor can it have 70 yods surrounding its centre because there is no
integer value of n for which 6n = 70. However, two joined Type A hexagons have 70 yods.
(2) The 73rd Tree from the top of CTOL is the 19th Tree from its base.
These numbers are the populations of the largest and the smallest of the set of seven polygons making up the inner
Tree of Life.
(3) 73 is the 21st prime number. The
73rd prime number is 367, which is the number of stages of descent of the Lightning Flash from the top of
CTOL to its base [1]. The dodecagon therefore encodes this important parameter of
CTOL.
(4) The 73rd SL in CTOL is Chesed of the 12th tree,
which is the 24 (= 1×2×3×4)th SL on the Pillar of Mercy. The 26th SL on the central Pillar of
Equilibrium emanates 73 SLs. This relates the Godname number of Chokmah to its number
value.
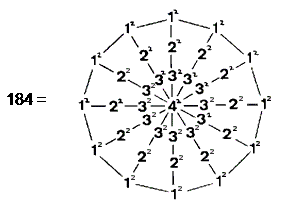
(5) A 12-fold array of integers 20, 30 & 40 surrounding the integer 1 generates the number
1081 of Tiphareth:
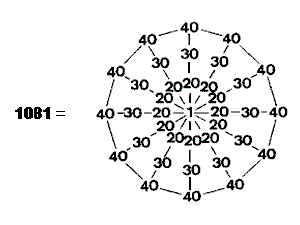
(6) A 12-fold array of the integers 1, 2, 3 & 4 generates the Godname number 76 of Tiphareth:
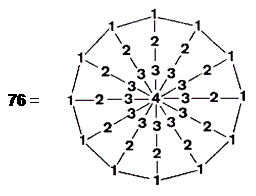
(7) A 12-fold array of the squares of 1, 2, 3 & 4 generates the number
This is the number of SLs on the central pillar of CTOL. The sum of the 36 squares surrounding the centre is 168, which is the gematria number of Cholem Yesodoth, the Mundane Chakra of Malkuth. It is the number of SLs on the central pillar of CTOL down to (and including) the highest point of the 7‑tree representing in Theosophical terms the "physical plane" — the physical universe, which is the Malkuth level of the cosmic physical plane (see here), itself the Malkuth level of CTOL. This dodecagonal array of the squares of 1, 2, 3 & 4 is a representation of the number of SLs on the central pillar of CTOL, its centre (42) denoting the 16 SLs on the central pillar below the apex of the 7-tree mapping the space-time continuum.
(8) A 12-fold array of the cubes of 1, 2, 3 & 4 generates the gematria number 496 of Malkuth:
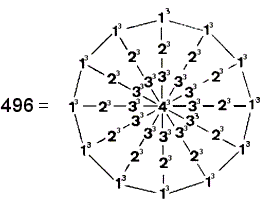
The dodecagon embodies both arithmetically and geometrically the structure of superstrings and their unified forces, that is, the Malkuth level of the Tree of Life in the subatomic world.
(9) The sum of the 72 integers 2, 3 & 4 surrounding the central integer 1 in the tetractys-divided dodecagon is:
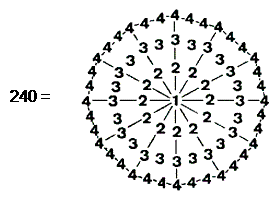
The dodecagon provides a representation of not only the number of roots of the superstring group E8×E8 but also the number of non-zero roots of E8. Of the 240 yods other than centres of polygons on the boundaries of the 48 tetractyses of the seven separate Type A polygons, 144 yods are on the boundaries of the latter. This is the sum of the 36 '4's on the boundary of the dodecagon. There are 96 yods other than centres on boundaries of tetractyses inside the seven polygons. This is the sum of the 36 internal integers surrounding the centre of the dodecagon. This remarkable representation of the number 240 reproduces arithmetically the boundary and internal yod populations of the seven separate polygons. As explained in The holistic pattern, the number 240 is found embodied in all sacred geometries/holistic systems. For example, 240 points, lines & triangles surround the bindu at the centre of the 2-dimensional Sri Yantra (see here).
(10) The sum of the first 73 integers is 2701 = 73×37. Assigning the first 37 odd integers to the internal yods and the 36 even integers to the boundary yods, the sum of the internal integers = 1369 = 372. The sum of the boundary integers = 1332 = 36×37.
(11) Sum of squares of first 73 integers = 132349 = 49×73×37.
Sum of squares of 37 internal integers = 67525 = 25×73×37.
Sum of squares of 36 boundary integers = 64824 = 24×73×37.
These numbers are generated by assigning the sum 73×37 of the first 73 integers to, respectively, each of the 49 yods of an octagon, its 25 internal yods and its 24 boundary yods. The octagonal representation of the number of EL ChAI reproduces the arithmetic properties of the dodecagon.
(12) 73 is the
ratio
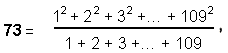
where 109
is the 55th odd integer. Hence:
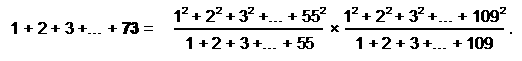
This shows the connection between the number of Chokmah and the tenth triangular number 55, which defines via the tetractys the population of SLs in CTOL. The tenth Fibonacci number is also 55, which is the number of points, lines & triangles in the 1-tree (see Article 50 (Part 1 & Part 2) for an examination of how Fibonacci numbers manifest in sacred geometries).
TYPE B DODECAGON
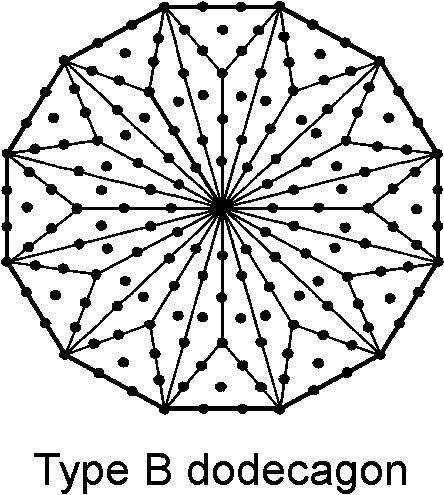 (1) The dodecagon has 181 yods, where 181 is the 91st odd integer. Therefore, the Type A
dodecagon embodies the number of Chokmah, whilst its Type B version is arithmetically connected to the number
of Trees in CTOL. Of the 181 yods, 156 yods are hexagonal. This, remarkably, is the sum of the values of all
11 combinations of the letters of YHVH, the Godname of Chokmah (see here). It is also the number of SLs in every 26 Trees. The Type B dodecagon has
144 internal yods surrounding its centre — the same number as seven, separate Type A
polygons.
(1) The dodecagon has 181 yods, where 181 is the 91st odd integer. Therefore, the Type A
dodecagon embodies the number of Chokmah, whilst its Type B version is arithmetically connected to the number
of Trees in CTOL. Of the 181 yods, 156 yods are hexagonal. This, remarkably, is the sum of the values of all
11 combinations of the letters of YHVH, the Godname of Chokmah (see here). It is also the number of SLs in every 26 Trees. The Type B dodecagon has
144 internal yods surrounding its centre — the same number as seven, separate Type A
polygons.
(2) Two separate dodecagons have 312 hexagonal yods.
Enfolded, they have
|
31 |
||||
| 31 | 31 | |||
| 310 = |
31 |
31 |
31 |
|
| 31 | 31 | 31 | 31 |
hexagonal yods, that is, 155 hexagonal yods are associated with each
one:
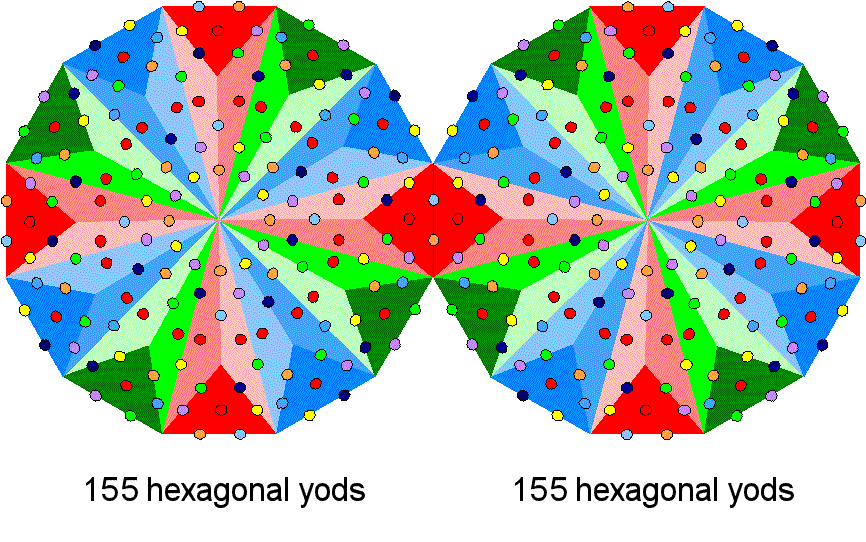
The enfolded Type B dodecagon embodies the number 155 of ADONAI MELEKH, the Godname of Malkuth. This is no coincidence, for the dodecagon encodes through its various transformations basic dynamical and structural parameters of superstrings, which are the Malkuth aspect of the subatomic Tree of Life, as will be shown shortly.
(3) 181 is the ratio
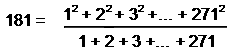
where 271 is the 136th odd integer and
| 1 | 2 | 3 | 4 | |
5 |
6 |
7 |
8 |
|
| = | 9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 , |
showing how the 91st odd integer is related to the Pythagorean integers 1, 2, 3 & 4 by the Godname number 15 of Chokmah and to the Pythagorean Tetrad by the 4×4 square array of the first 16 integers.
(4) Sum of first 181 integers = 16471 = 181×91, i.e., this number is generated by assigning the number 91 to each yod in the dodecagon. Hence, the Type B dodecagon encodes the number of Trees in CTOL as the arithmetic mean of the integers 1–181 that can be assigned to its yods. The tenth regular polygon embodies not only the number 73 of Chokmah (“wisdom”) but also the number of Trees in CTOL. The number of yods inside the dodecagon = 181 − 36 = 145 = 1! + 4! + 5!. This is one of only four numbers that are the sums of the factorials of their digits [2]. 145 is also the fourth number to be the sum of two squares in two different ways: 145 = 122 +12 = 82 + 92, illustrating how the Tetrad Principle, according to which the fourth member of a class of mathematical object, is a parameter of holistic systems, determines how many yods are inside the boundary of the dodecagon.
(5) Assigning integers 1–181 to its yods with 1 at its centre:
(6) Sum of squares of the first 181 integers = 1992991 = 181×91×121, where 181, 91 & 121 are the populations of, respectively, the Type B dodecagon, hexagon and octagon. Sum of squares of 145 internal integers = 1026745 = 145×97×73, where 73 is the number of yods in a Type A dodecagon and the 49th odd integer:
97 = 21 + 26 + 50
is the sum of the Godname
numbers of the Supernal Triad. 97 is the ratio:
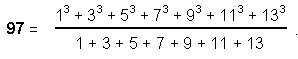
(7) Of the 181 yods, 13 yods
are corners of the 12 sectors, so that 168 yods need to be added to turn a dodecagon into a Type B
dodecagon:
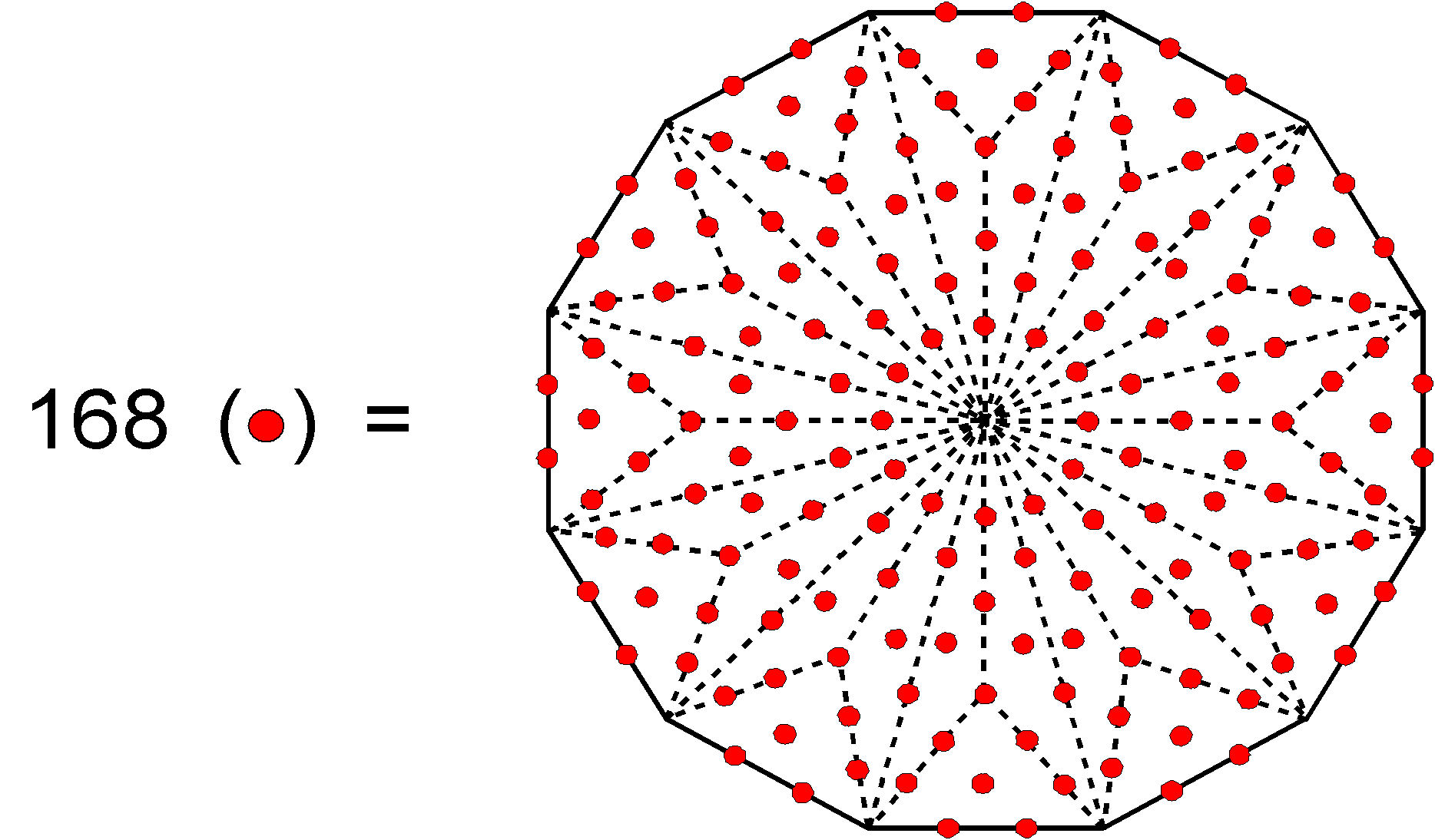
This polygon embodies the superstring structural parameter 168 as the number of yods required to
transform its 12 sectors. Two joined dodecagons contain 358 yods. They comprise 22 corners of the dodecagons and
336 yods (168 yods associated with each dodecagon) that are made up of 310
(=31×10) hexagonal yods and 26 corners of tetractyses:
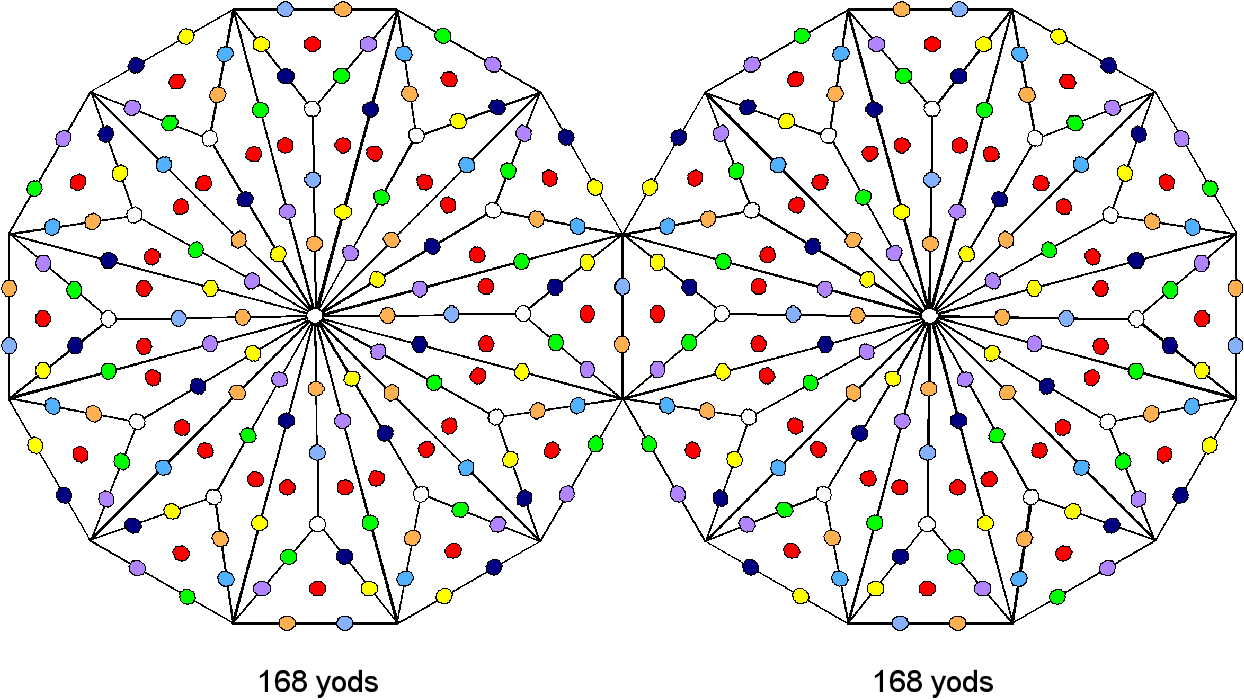
This shows how EL, the Godname of Chesed with number value 31 and YAHWEH, the Godname of Chokmah
with number value 26, prescribe the holistic parameter 336. The
72 tetractyses in the pair of Type B dodecagons have 48 corners (24
associated with each dodecagon). This 24:24 division is characteristic of holistic systems, so that it may be
inferred that the two joined Type B dodecagons constitute such a system. We encountered evidence for this in the
discussion of the two joined Type A dodecagons, each of which has the same number of yods associated with it as
there are in the Tree of Life. Other evidence is provided by the table of geometrical properties of the polygons, which indicates that 24 sides
and 24 corners & triangles surround the centre of a Type A dodecagon. The
168:168 division of yods other than dodecagonal corners is further
evidence of their holistic nature, being found in sacred geometries such as the Sri Yantra (see here) and the disdyakis triacontahedron (see here). The fact that 120 corners, sides & triangles
surround the centre of a Type B dodecagon is yet more evidence because this number is another major parameter of
holistic systems (for example, 120 yods line the sides of the seven enfolded polygons of the inner Tree of Life
(see here), and the disdyakis triacontahedron has 120 faces).
The Type B dodecagon is the polygonal realization of the seven enfolded
polygons. It comprises 24 corners and 60 sides of 36 triangles that surround its
centre. These 120 geometrical elements are symbolized by the 120 yods on the boundaries of the seven enfolded
polygons:
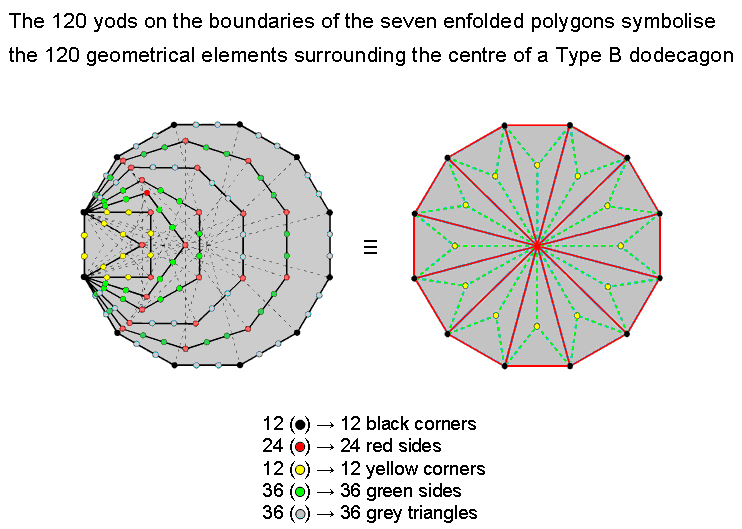
The 36 corners of the enfolded polygons symbolize the 36 corners, sides & internal sides of the sectors of the Type A dodecagon and the 84 hexagonal yods on the 42 sides of the enfolded polygons symbolize the extra 84 corners, sides & triangles needed to turn the Type A dodecagon into the Type B dodecagon. The 12 yellow hexagonal yods on the sides of the triangle & square symbolize the 12 corners of triangles inside the dodecagon, the 36 green hexagonal yods on the sides of the pentagon, hexagon & decagon symbolize the 36 internal sides of triangles and the 36 blue hexagonal yods on the sides of the octagon & dodecagon symbolize the 36 triangles. Such detailed correspondence cannot, plausibly, be dismissed as coincidence.
24 corners, 60 sides & 36 triangles surround the centre of a Type B dodecagon. Hence, two separate Type B dodecagons have 48 corners, 120 sides & 72 triangles surrounding their centres, i.e., their 240 geometrical elements comprise 168 corners & sides and 72 triangles. This 72:168 division is characteristic of holistic systems and many examples can be found on this website (for other examples, see The holistic pattern). Its counterpart in the rank-8, exceptional Lie group E8 appearing in superstring theory are the 72 roots of E6, the rank-6, exceptional subgroup of E8 and the 168 roots of the latter that are not roots of E6.
Enfolded, two Type B dodecagons have 48 corners and 119 sides of 72 triangles, i.e., 239 geometrical elements, so that 236 elements are outside their shared root edge. This is the number of yods lining the 83 sides of the (7+7) enfolded polygons. It is also the number of corners, sides & triangles in the 42 triangles of the 2-dimensional Sri Yantra that surround its central triangle (see Table 4 on p. 8 & Fig. 9 on p. 9 of Article 35). 236 is a parameter of holistic systems, as is the number 48, being the number value of Kokab, the Mundane Chakra of Hod. As pointed out in The holistic pattern, such systems display a 24:24 division in this number. It manifests in the two joined Type B dodecagons as the 24 corners associated with the 36 triangles in each one.
TYPE A + TYPE B DODECAGON
A separate Type A dodecagon and a Type B dodecagon have 254 yods, of which
216 are hexagonal yods. The pair of dodecagons embodies the number of Geburah, whilst its Godname number
36 is the number of yods on the boundary of each dodecagon. Enfolded in the Tree of Life, they have 250 yods
(214 hexagonal yods & 36 corners of tetractyses). 248 yods surround their
centres:
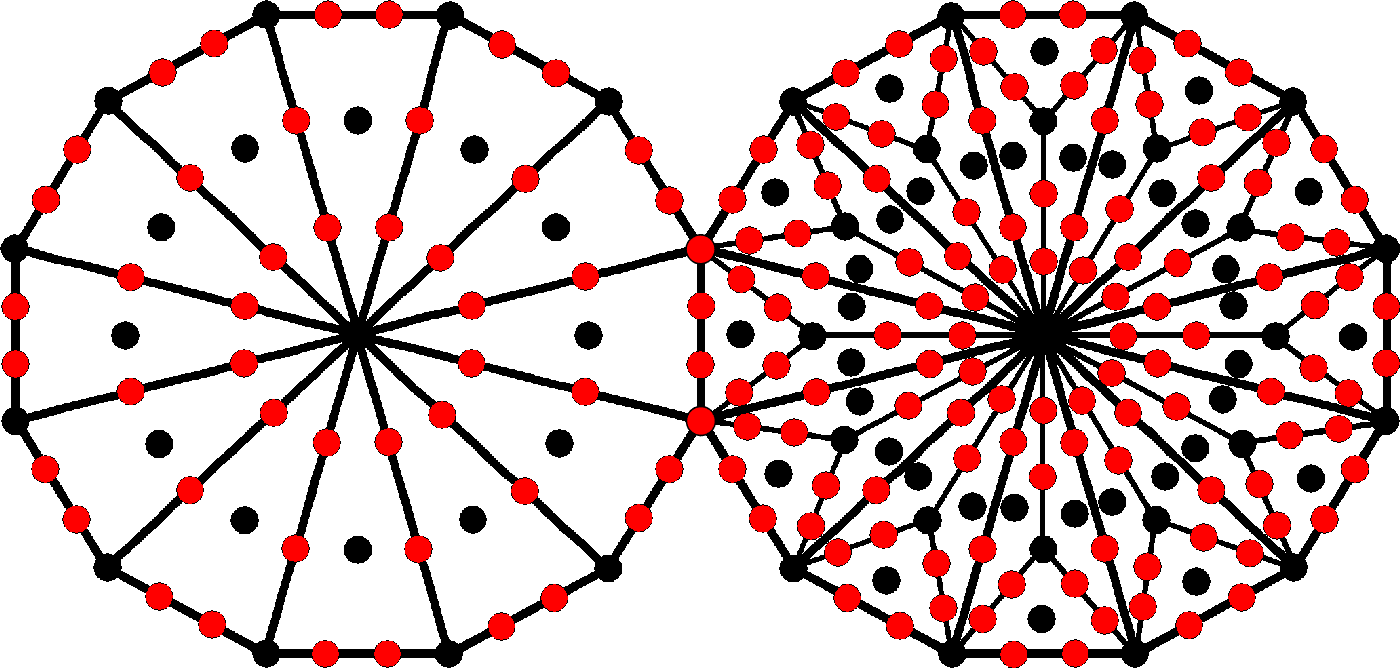
80 black yods are either corners or centres of tetractyses and 168 red yods are, apart from the two endpoints of the root edge, hexagonal yods on sides of tetractyses. We see that the dodecagon encodes the dimension 248 of the superstring symmetry group E8, an encoding that is prescribed by ELOHA, the Godname of Geburah with number value 36, because there are 36 yods delineating the boundary of each dodecagon. This amazing property is further reason why the dodecagon should be associated with Malkuth, the superstring-filled universe. The 80:168 division of 248 corresponds to the division of the 248 yods making up the lowest five overlapping Trees of Life as far as the 31st SL into the 80 yods of the 1-tree and the remaining 168 yods up to Chesed of the fifth Tree (see here).
A Type A dodecagon comprises 13 corners and 24 sides of 12 triangles; a Type B dodecagon comprises 25 corners and 60 sides of 36 triangles. The separate pair of dodecagons has 168 geometrical elements surrounding their centres (84 corners & triangles, 84 sides). This 84:84 division of 168 is characteristic of holistic systems (other examples are pointed out in The holistic pattern). Their centres are surrounded by 168 geometrical elements when separate and 248 yods when joined. Amazingly, both the dimension 248 of the gauge symmetry group E8 and the structural parameter 168 of the subquark state of the E8×E8 heterotic superstring are embodied in these two types of dodecagons when considered together! The reason for this is simple: superstrings are part of the Tree of Life blueprint for the subatomic world and the dodecagon is its polygonal realization. Here is remarkable evidence for how the tenth regular polygon (i.e., how the Pythagorean Decad) embodies the dynamics and structure of the subquark superstring paranormally described over a century ago by Annie Besant and C.W. Leadbeater.
The 12 corners of a dodecagon consist of four sets of three corners, spaced 120° apart. Their cosmic counterpart are the 12 signs of the zodiac listed in the table below:
| Symbol | Sign name | English name | Element | Polarity | Period of birth |
|
|
Aquarius |
The Water Carrier | Air | Positive |
January 21 - February 19 |
 |
Pisces |
The Two Fish | Water | Negative | February 20 - March 20 |
 |
Aries | The Ram | Fire | Positive | March 21 - April 20 |
 |
Taurus | The Bull | Earth | Negative | April 21 - May 20 |
 |
Gemini | The Twins | Air | Positive | May 21 - June 20 |
 |
Cancer | The Crab | Water | Negative | June 21 - July 22 |
 |
Leo | The Lion | Fire | Positive | July 23 - August 22 |
 |
Virgo | The Maiden | Earth | Negative | August 23 - September 22 |
 |
Libra | The Scales | Air | Positive | September 23 - October 22 |
 |
Scorpio | The Scorpion | Water | Negative | October 23 - November 21 |
 |
Sagittarius | The Archer/Centaur | Fire | Positive | November 22 - December 21 |
 |
Capricorn | The Sea-goat | Earth | Negative | December 22 - January 20 |
Each sign is associated with one of the four Elements (Fire, Air, Water & Earth), so that the 12 signs are grouped into four sets of three. This is shown in the diagram below by the red and blue triangles linking each set of three signs. Fire and Air signs are considered positive, yang, active, dominant or extrovert, masculine signs; while Water and Earth signs are considered negative, yin, introvert, feminine signs. The same pattern is found in the 12 acupuncture meridians (see here), which group into four triplets:
The six Yang Meridians and the six Yin Meridians correspond, respectively, to the positive astrological signs and to the six negative signs.
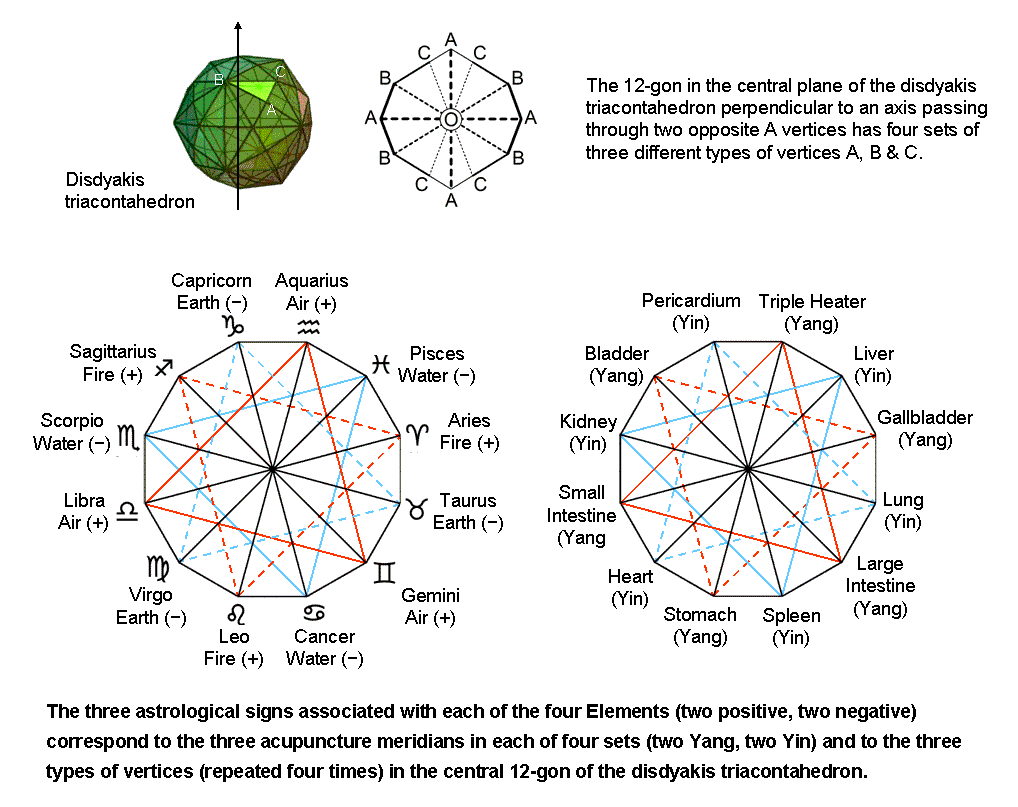
The disdyakis triacontahedron is the outer form of the Polyhedral Tree of Life. The counterparts in this polyhedron of the 4×3 pattern in the 12 astrological signs and the 12 meridians are the four instances of the three types of vertices A, B & C in the 12-gon formed in the central plane of the polyhedron by 12 vertices (see here). The counterparts of the six positive signs and six negative signs and the six Yang meridians and the six Yin meridians are the six corners in one half of the 12-gon and their six mirror images in its other half.
An analogous pattern is exhibited in the 12 roots of G2, the rank-2, simply-connected Lie group that some physicists are suspecting may play a central role in the sought-after M-theory that generalizes supergravity and the five superstring theories. This is because it is the group of automorphisms of the octonions, which seem to be the natural basis of the gauge symmetry group E8 that is present in E8×E8, the symmetry group that is known (together with SO(32)) to describe interactions of superstrings that are free of quantum anomalies. Its 14 roots consist of a pair of simple roots with rectangular coordinates α0 = (0, 1, −1) and α0' = (1, −2, 1) and six pairs of other roots, one member of each pair being the inversion of the other:
| α1 = (1, −1, 0) | α1' = (−1, 1, 0) | |
| α2 = (−1, 0, 1) | α2' = (1, 0, −1) | |
| α3 = (0, 1, −1) | α3' = (0, −1, 1) | |
| α4 = (2, −1, −1) | α4' = (−2, 1, 1) | |
| α5 = (−1, 2, −1) | α5' = (1, −2, 1) | |
| α6 = (−1, −1, 2) | α6' = (1, 1, −2) |
The four triplets of roots are located at the corners of four triangles that form two nested Stars of David:
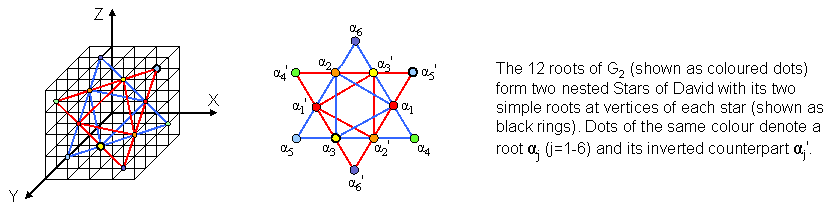
For further details, see Article 32.
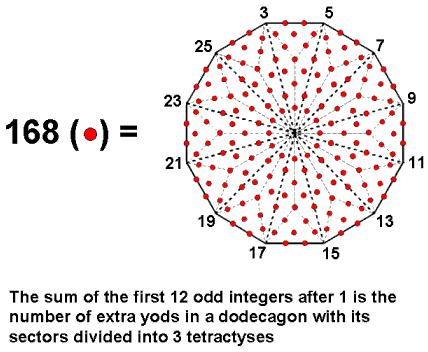
These examples serve to illustrate the universal manifestation of the dodecagon. Both arithmetically and through its yod composition, it embodies the number 168 of Cholem Yesodoth as the primary structural parameter of the superstring because this is the sum of the 12 odd integers after 1 that can be assigned to the corners of the dodecagon, the Type B version of which contains 168 yods other than these corners:
TYPE C
DODECAGON
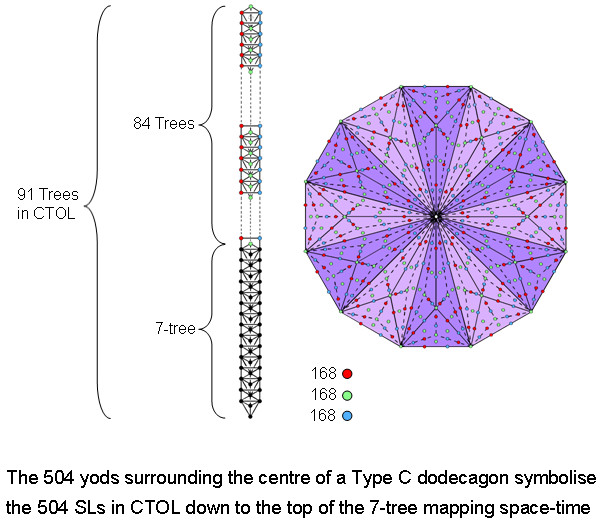
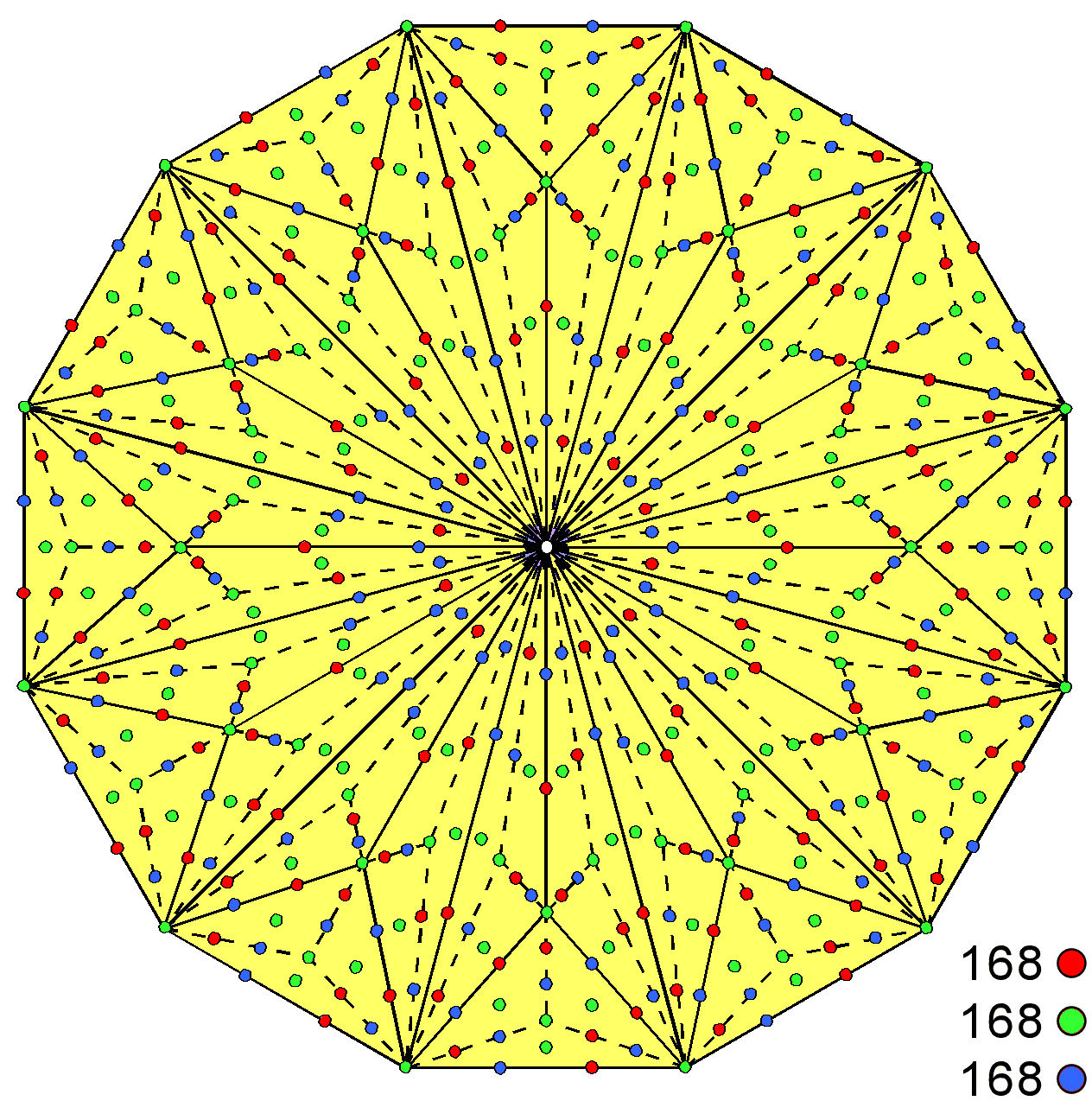
The dodecagon has 504 yods surrounding its centre. 500
(=50×10) yods outside its root edge are needed to generate it, starting with its centre. This
shows how ELOHIM, the Godname of Binah with number value 50, prescribes the polygonal version of
the Tree of Life. The 504 yods comprise the 168 green yods surrounding its centre that are
either corners of tetractyses or hexagonal yods at their centres and 336 (=2×168) hexagonal yods lining their sides
(168 red yods & 168 blue yods). The superstring significance of this
168:2×168 division is discussed in #15 at Wonders of superstrings
(see also #31 at Wonders of
correspondences). The number 504 is a
parameter of holistic systems, e.g., 5040 (=504×10) geometrical elements surround the axis of the
disdyakis
triacontahedron
|
|
|
504 yods surround the centre of a Type C dodecagon. |
when its faces and interior triangles formed by edges and sides of sectors are Type A triangles (see here), and 504 geometrical elements on average surround the axes of the five Platonic solids when their faces are Type A regular polygons and when their interior triangles formed by their edges and by the sides of sectors of their faces are Type A triangles (see here). In the context of CTOL, the meaning of this number is that it is the number of SLs down to the top of the 7-tree, below which are 46 SLs:
550 = 504 + 46.
As the 7-tree maps the seven subplanes of the physical plane, that is, the space-time continuum, there are 504 SLs in CTOL above the point where space and time exist as attributes of physical awareness:
 |
 |
|
There are 168 red SLs above the 7-tree on the left-hand Pillar of Judgement of the 91 Trees of Life representing CTOL. There are 168 blue SLs above the 7-tree on the right-hand Pillar of Mercy. 168 green SLs span the central Pillar of Equilibrium down to the top of the 7-tree. There are 14 green yods per sector of the Type C dodecagon that are either corners of tetractyses or hexagonal yods at their centres. The 9 tetractyses per sector have 14 sides, a red and a blue hexagonal yod lying on each one. Hence, the 504 yods surrounding the centre of the dodecagon comprise (12×14=168) yods that are either red, green or blue. They symbolise the three sets of 168 SLs lining the three pillars of CTOL down to the top of the 7-tree. |
An alternative scheme: there are 5 green corners and 9 green hexagonal yods at the centres of tetractyses per sector of the dodecagon, which has altogether (12×14=168) green yods. The 108 tetractyses have 168 sides lined by 336 hexagonal yods (168 red yods and 168 blue yods). The centre of the dodecagon is surrounded by 504 yods consisting of three sets of 168 yods (red, green & blue). |
Other examples of this parameter are discussed here.
Notes
1. Proof: the number of vertical
stages of descent of the Kabbalistic "Lightning Flash" in n overlapping Trees of Life = 4n + 3. It descends in
(4×91 + 3 = 367) vertical stages from the top of the 91st Tree.
2. The Penguin Dictionary of Curious and Interesting Numbers, David Wells (Penguin Books, 1988), p. 140.
3. Proof: the number of yods in n overlapping Trees of Life ≡ Y(n) = 50n + 20. There are (Y(27)=1370) yods in 27 overlapping Trees.