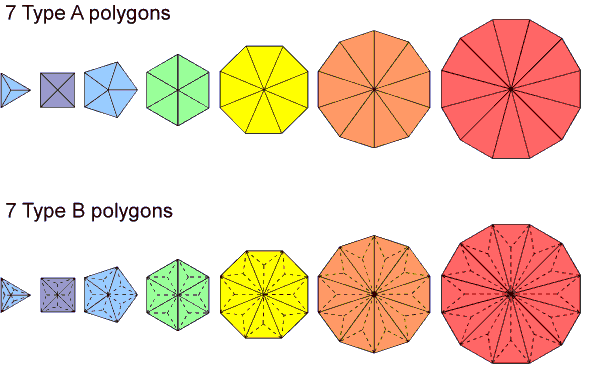
Polygons as the geometrical expression of numbers
A so-called "n-gon" (a polygon with n corners or sides) can be divided, firstly, into its n sectors. It is what we call a "Type A polygon" (the term also applies to a polygon with its sectors turned into tetractyses). Then each triangular sector can be divided into three sectors, i.e., each sector can be turned into a Type A triangle. This is a "Type B polygon" (it is also this when its 3n triangles are turned into tetractyses). Such division can proceed indefinitely, generating Type C polygons, each of whose sectors is a Type B triangle, then Type D polygons, each of whose sectors is a Type C triangle, etc. The nomenclature used here is not entirely adequate because the English alphabet has only 26 letters, whereas the number of ways (for any given n) an n-gon can be divided up is infinite. However, discussion here will be mostly confined to Type A and Type B polygons — the first four types at the most — and so the nomenclature will serve its purpose, even though it cannot apply for any level of division of polygons (Article 65 provides nomenclature for the general case). The way in which the Type C triangle embodies the dimension 248 of the rank-8, exceptional Lie group E8 used in superstring theory is discussed here.
The regular polygons are the simplest way of symbolizing
integers by the number of their corners or sides, starting with the integer 3 as the number of corners or sides of
the equilateral triangle. However, there are three more subtle ways in which polygons embody numbers, whether
regular or not:
1. Number of points, lines & triangles needed for their
construction.
There are seven possible combinations of these three geometrical elements or building blocks:
1. point, 2. line, 3. triangle, 4. point+line, 5. point+triangle, 6. line+triangle, 7. point+line+triangle.
A polygon embodies in its geometry the seven corresponding numbers of such combinations. If the numbers of various combinations of geometrical elements surrounding the centre of the polygon are considered as well (of which four new ones exist), a polygon embodies 11 numbers. A Type A n-gon is composed of (n+1) corners and 2n sides of n triangles, i.e., (4n+1) geometrical elements, where "1" refers to its centre. A Type B n-gon has (2n+1) corners and 5n sides of 3n triangles, i.e., (10n+1) geometrical elements. General formulae for the mth type of n-gon (the so-called "mth-order n-gon") will be derived shortly ( see also Article 65).

Table 1 displays the geometrical composition of the seven types of Type A and Type B regular polygons making up the inner Tree of Life:
Table 1. Geometrical composition of the seven Type A or Type B polygons in the inner Tree of Life.
|
Triangle |
Square |
Pentagon | Hexagon | Octagon |
Decagon |
Dodecagon |
Total | |||||||||
| A |
B |
A | B | A | B | A | B | A | B | A | B | A | B | A | B | |
| Number of corners | 3+1=4 | 6+1=7 | 4+1=5 | 8+1=9 | 5+1=6 | 10+1=11 | 6+1=7 | 12+1=13 | 8+1=9 | 16+1=17 | 10+1=11 | 20+1=21 | 12+1=13 | 24+1=25 | 48+7=55 | 96+7=103 |
| Number of sides | 6 | 15 | 8 | 20 | 10 | 25 | 12 | 30 | 16 | 40 | 20 | 50 | 24 | 60 | 96 | 240 |
| Number of triangles | 3 | 9 | 4 | 12 | 5 | 15 | 6 | 18 | 8 | 24 | 10 | 30 | 12 | 36 | 48 | 144 |
| Number of geometrical elements | 12+1=13 | 30+1=31 | 16+1=17 | 40+1=41 | 20+1=21 | 50+1=51 | 24+1=25 | 60+1=61 | 32+1=33 | 80+1=81 | 40+1=41 | 100+1=101 | 48+1=49 | 120+1=121 | 192+7=199 | 480+7=487 |
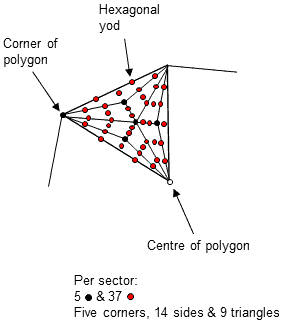
(The number "1" in some cells denotes the centre of a polygon; as usual, the gematria number values of the ten Sephiroth in the four Kabbalistic Worlds (see here) are in bold). The seven Type A polygons have 192 geometrical elements surrounding their centres. 384 geometrical elements surround the 14 centres of both sets of seven polygons. This 192:192 division is characteristic of holistic systems. For example, as discussed here, the table of 64 hexagrams used in the ancient Chinese divination system of I Ching contains 384 lines & broken lines (192 in each diagonal half). Surrounding the centres of the seven Type B polygons are 240 sides and 240 corners & triangles, i.e., 480 geometrical elements. This 240:240 division is another feature of holistic systems. Its counterpart in E8×E8 heterotic superstring theory is the set of 240 roots of each group E8 in the symmetry group E8×E8. It manifests in each set of seven separate Type A polygons as their 240 hexagonal yods (see table below) when their 48 sectors are tetractyses (see also here & here).
2. Numbers of yods needed to construct their sectors from tetractyses.
A Type A n-gon has (6n+1) yods made up of (n+1) corners & 5n hexagonal yods. A Type B n-gon has (15n+1) yods made up of (2n+1) corners & 13n hexagonal yods. Notice the appearance in the algebraic expression for its yod population of the number value 15 of YAH (יה), the older version of the Godname assigned to Chokmah.
.png)
Table 2 displays the yod populations of the seven regular polygons comprising the inner Tree of Life:
Table 2. Yod composition of the seven Type A or Type B polygons.
|
Triangle |
Square |
Pentagon | Hexagon | Octagon | Decagon | Dodecagon | Total | |||||||||
| A | B | A | B | A | B | A | B | A | B | A | B | A | B | A | B | |
| Number of corners | 3+1=4 | 6+1=7 | 4+1=5 | 8+1=9 | 5+1=6 | 10+1=11 | 6+1=7 | 12+1=13 | 8+1=9 | 16+1=17 | 10+1=11 | 20+1=21 | 12+1=13 | 24+1=25 | 48+7=55 | 96+7=103 |
| Number of hexagonal yods | 15 | 39 | 20 | 52 | 25 | 65 | 30 | 78 | 40 | 104 | 50 | 130 | 60 | 156 | 240 | 624 |
| Number of yods | 18+1=19 | 45+1=46 | 24+1=25 | 60+1=61 | 30+1=31 | 75+1=76 | 36+1=37 | 90+1=91 | 48+1=49 | 120+1=121 | 60+1=61 | 150+1=151 | 72+1=73 | 180+1=181 | 288+7=295 | 720+7=727 |
As pointed out earlier, each set of seven polygons has not only 240 sides and 240 corners & triangles when they are Type B polygons but also 240 hexagonal yods when they are Type A. The 240:240 division has now extended from one set to both sets. The number 240 is a parameter of all holistic systems (see here; scroll down to "240 = 72 + 168").
3. Sums of consecutive integers (always starting with 1) assigned to yods in the polygon (always starting at its centre).
A Type A n-gon has (3n+1) yods inside its boundary and 3n yods (i.e., one less) on its boundary. So it contains (6n+1) yods. As this is an odd integer, the sum of the first (6n+1) integers that can be assigned to its yods:
1 + 2 + 3 + ... + (6n+1) = (3n+1)(6n+1),
contains (3n+1) odd integers and 3n even integers (i.e., one less). It is, therefore, mathematically possible, as well as natural, to assign the odd integers up to (6n+1) to internal yods, starting with the integer 1 at its centre, and to assign, starting with 2, the even integers up to 6n to yods on the sides of the polygon. The sum of the former is:
1 + 3 + 5 + ... + (6n+1) = (3n+1)2
and the sum of the latter is:
2 + 4 + 6 + ... + 6n = 3n(3n+1).
The sum of all (6n+1) integers that can be assigned to the yods in a Type A n-gon is (3n+1)(6n+1). Hence, a Type A polygon embodies three numbers that are these three sums. Notice that the arithmetic means of the odd integers, the even integers and all the integers are the same, namely, 3n + 1, which is the number of internal yods in the Type A n-gon. The only one of the seven regular polygons making up the inner form of the Tree of Life for which this is a Godname number is the decagon (n = 10). In this polygon, each mean is 31, which is the number of EL, the Godname of Chesed. This acquires significance in view of the fact that the Type A decagon with its ten sectors turned into tetractyses and containing 61 yods is the polygonal counterpart of the 61 SLs up to the highest Chesed of ten overlapping Trees, which is a representation of the Tree of Life in which each Sephirah is replaced by a Tree of Life. A Type B polygon also embodies three numbers, although, having a yod population of (15n+1) that can be either even or odd and not having the same number of yods on its boundary as in its interior, assignment of odd integers to internal yods and even integers to boundary yods is no longer possible, so that the interior integers must be 1, 2, 3, ... (12n+1) and the boundary integers must be (12n+2), (12n+3), ... (15n+1).
The table above shows that the seven separate Type B polygons contain 727 yods. This number is the 129th prime number, where 129 is the gematria number value of ELOHIM SABAOTH, the Godname of Hod (see here). This is a spectacular example of how the Godnames of the ten Sephiroth prescribe the properties of the inner Tree of Life (in the case of the seven Type A polygons, see pages 25-34 in Sacred geometry/Tree of Life).
The number of yods surrounding the centres of the seven Type B polygons = 720 = 10×72. This is the number of yods that surround the centre of a decagon with 2nd-order tetractyses as sectors, each sector having 72 such yods:
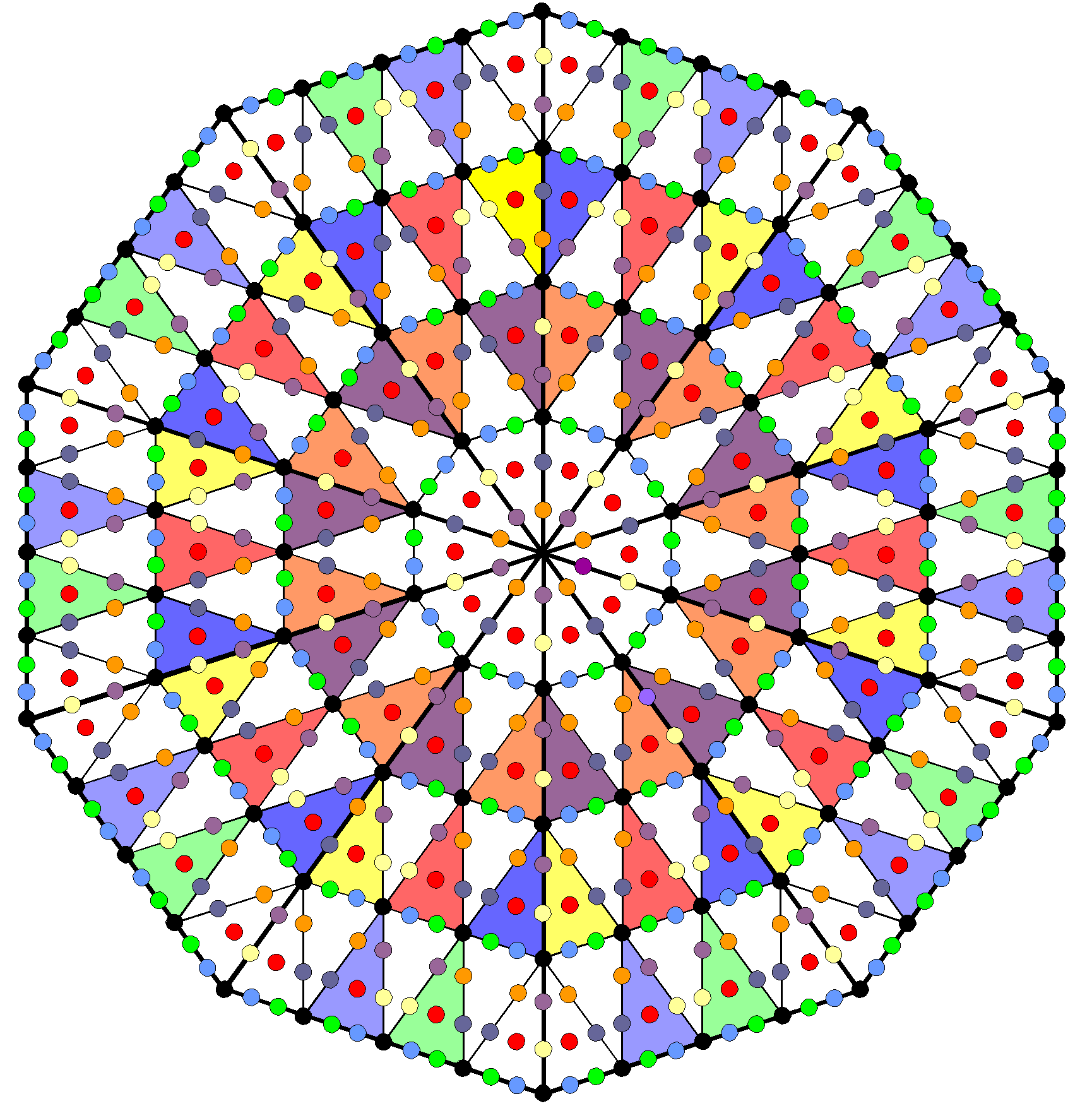 |
| 720 yods surround the centre of a decagon with 2nd-order tetractyses as its sectors. |
This demonstrates the archetypal power of the Decad symbolised by the 10-corner decagon to determine the properties of holistic systems.
It needs to be emphasized that we are dealing here not with ordinary geometry but with sacred geometry. Because the seven polygons of the inner Tree of Life are constructed from tetractyses — the template of all straight-line sacred geometries — the numbers thereby generated by this transformation are not arbitrary or insignificant. Instead, they turn out to be numbers that characterize all sacred geometries in a global sense, as demonstrated many times in this website. In other words, they are universal parameters of sacred geometry. As such, their presence helps to distinguish what is true sacred geometry, namely, the representation of the divine archetypes, from what is merely the kind of axiomatic geometry that has been studied by mathematicians ever since the days of Euclid and taught to school children for hundreds of years.
The geometrical & yod compositions of polygons
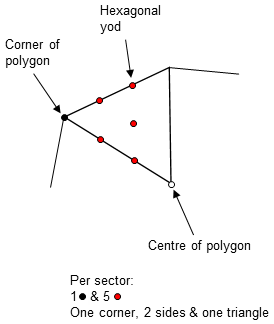
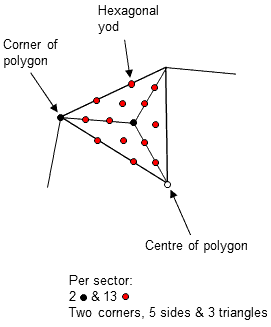
Let us define a 1st-order polygon P1 as a polygon divided into its sectors, a 2nd-order polygon P2 as a P1 whose sectors are each divided into three sectors, etc. P1 is the Type A polygon, P2 is the Type B polygons, P3 is the Type C polygon, etc. A sector of the first three orders of polygons is shown below:
 |
 |
 |
|
|
|
|
The number of corners per sector of the nth-order polygon Pn (n = 1, 2, 3, 4, etc) increases with n as 1, 2, 2 + 31, 2 + 32, etc. The number of sides increases as 2, 2 + 31, 2 + 31 + 32, 2 + 31 + 32 + 33, etc. The number of triangles increases as 1, 31, 32, 33, etc. Including its centre, Pn has cn corners, sn sides & tn triangles, where:
cn = 1 + 30 + 31 +... + 3n−2 = (1+3n−1)/2,
sn = 1 + 30 + 31 + +... + 3n−1 = (1+3n)/2,
and
tn = 3n−1.
Therefore,
cn + tn = (1+3n−1)/2 + 3n−1 = (1+3n)/2 = sn,
i.e., the number of corners & sides per sector of Pn is equal to the number of sides per sector of the triangles in each sector. This means that the number of corners & triangles surrounding the centre of Pn is equal to the number of sides of its triangles. This division of the geometrical elements surrounding the centre of a polygon into two equal sets is highly significant, having important implications that will be revealed in the discussion elsewhere in this website of how sacred geometries encode the group mathematics and structure of E8×E8 heterotic superstrings.
The number of corners, sides & triangles per sector ≡ gn = cn + sn + tn = 2sn = 1 + 3n. Including its centre, the number of corners in an nth-order m-gon ≡ Cn(m) = 1 + mcn = 1 + m(1+3n−1)/2. The number of sides ≡ Sn(m) = msn = m(1+3n)/2. The number of triangles ≡ Tn(m) = mtn = 3n−1m. The number of geometrical elements in an nth-order m-gon ≡ Gn(m) = Cn(m) + Sn(m) + Tn(m) = 1 + mgn = 1 + m(1+3n).
The number of hexagonal yods in an nth-order m-gon ≡ hn(m) = 2Sn(m) + Tn(m) = m(1+3n−1+3n). Including the centre of the m-gon, the number of yods ≡ Yn(m) = Cn(m) + hn(m) = 1 + m(3+3n+1)/2.
Seven separate
polygons
The seven types of regular polygons present in the
inner form of the Tree of Life have 48 corners. The number of geometrical elements in the seven separate
nth-order polygons = ∑Gn(m) = 7 + ∑mgn = 7 + gn∑m = 7 + 48gn = 7
+ 48(1+3n) = 55 + 48×3n. "55" is the number of corners of their
48 sectors.
The number of hexagonal yods in the seven separate nth-order polygons ≡ Hn = ∑hn(m) = (1+3n−1+3n)∑m = 48(1+3n−1+3n) = 48 + 64×3n. The number of yods in the seven polygons ≡ Yn = ∑Yn(m) = ∑[1 + m(3+3n+1)/2 = 7 + 24(3+3n+1) = 7 + 72(1+3n) = 79 + 8×3n+2.
For future reference, Table 3 lists the numbers of corners, sides & triangles per sector for the first four orders of any polygon:
Table 3. Geometrical composition per sector for the first four orders of a polygon.
|
|
n |
Corners (cn) |
Sides (sn) |
Triangles (tn) |
Total (gn) |
| Type A |
1 |
1 |
2 |
1 | 4 |
| Type B |
2 |
2 |
5 |
3 | 10 |
| Type C |
3 |
5 |
14 | 9 | 28 |
| Type D |
4 |
14 |
41 | 27 | 82 |
Table 4 lists the yod populations of the first four orders of the seven types of polygons making up the inner Tree of Life:
Table 4. Yod populations of the first four orders of the seven types of polygons in the inner Tree of Life and their sums.
|
|
n |
Yn(3) |
Yn(4) |
Yn(5) |
Yn(6) |
Yn(8) |
Yn(10) |
Yn(12) |
Yn |
| Type A |
1 |
1 + 18 = 19 |
1 + 24 = 25 |
1 + 30 = 31 | 1 + 36 = 37 | 1 + 48 = 49 | 1 + 60 = 61 | 1 + 72 = 73 | 7 + 288 = 295 |
| Type B |
2 |
1 + 45 = 46 |
1 + 60 = 61 |
1 + 75 = 76 | 1 + 90 = 91 | 1 + 120 = 121 | 1 + 150 = 151 | 1 + 180 = 181 | 7 + 720 = 727 |
| Type C |
3 |
1 + 125 = 126 |
1 + 168 = 169 | 1 + 210 = 211 | 1 + 252 = 253 | 1 + 336 = 337 | 1 + 420 = 421 | 1 + 504 = 505 | 7 + 2016 = 2023 |
| Type D |
4 |
1 + 369 = 370 |
1 + 492 = 493 | 1 + 615 = 616 | 1 + 738 = 739 | 1 + 984 = 985 | 1 + 1230 = 1231 | 1 + 1476 = 1477 | 7 + 5904 = 5911 |
Seven enfolded polygons
The number of corners per sector of an (n−1)th-order polygon = cn−1 = (1+3n−2)/2. Hence, the
number of corners in a (n−1)th-order triangle = 1 + 3cn−1 = 1 + 3(1+3n−2)/2 =
(5+3n−1)/2. The number of corners in the seven separate nth-order polygons
= ∑Cn(m) = 7 + ½(1+3n−1)∑m = 7 +
24(1+3n−1) = 31 + 8×3n. When the polygons are enfolded, a corner of the pentagon
coincides with the centre of the decagon, a corner of the triangle coincides with the centre of the hexagon and the
nth-order triangle replaces a sector (an (n−1)th-order triangle) of the nth-order hexagon. Also, single sides of
five other polygons coincide with the root edge, so that the (5×2=10) corners that these sides join disappear. The
number of corners of triangles in the seven enfolded nth-order polygons ≡ Cn = 31 + 8×3n − 1 − 10 − (5+3n−1)/2
= (35+47×3n−1)/2. The number of corners in the (7+7) enfolded polygons = 2Cn − 2 = 33 + 47×3n−1.
The number of sides of triangles in an (n−1)th-order polygon = msn−1 = m(1+3n−1)/2. Hence, the number of sides in an (n−1)th-order triangle = 3(1+3n−1)/2. The number of sides in the seven separate nth-order polygons = ∑Sn(m) = ∑msn = ½(1+3n)∑m = 24(1+3n). The number of sides in the seven enfolded polygons ≡ Sn = 24(1+3n) − 5 − 3(1+3n−1)/2 = (35+47×3n)/2. The number of sides in the (7+7) enfolded polygons = 2Sn − 1 = 34 + 47×3n.
The number of triangles in an (n−1)th-order polygon = Tn−1(m) = 3n−2m. Hence, the number of triangles in an (n−1)th-order triangle = 3n−1. The number of triangles in the seven separate polygons = ∑Tn(m) = ∑3n−1m = 48×3n−1 = 16×3n. The number of triangles in the seven enfolded polygons ≡ Tn = 16×3n − 3n−1 = 47×3n−1. The number of triangles in the (7+7) enfolded polygons = 2Tn = 94×3n−1.
The number of geometrical elements in the seven enfolded polygons ≡ Gn = Cn + Sn + Tn = 35 + 47×3n. The number of geometrical elements in the (7+7) enfolded polygons = 2Gn − 3 = 67 + 94×3n, where 67 is the number value of Binah. As the topmost corner of each hexagon coincides with the bottom of a hexagon enfolded in the next higher Tree of Life, the number of geometrical elements that are intrinsic to the inner form of each Tree = 65 + 94×3n, where 65 is the number value of ADONAI, the Godname of Malkuth.
The number of hexagonal yods in the seven enfolded polygons ≡ Hn = 2Sn + Tn = 35 + 47×3n + 47×3n−1 = 35 + 188×3n−1. The number of hexagonal yods in the (7+7) enfolded polygons = 2Hn − 2 = 68 + 376×3n−1.
The number of yods in the seven enfolded polygons ≡ Yn = Cn + Hn = (35 + 47×3n−1)/2 + 35 + 188×3n−1 = ½(105 + 47×3n+1). The number of yods in the (7+7) enfolded polygons = 2Yn − 4 = 101 + 47×3n+1. Amazingly, 101 is the 26th prime number and 47 is the 15th prime number, where 26 is the number value of YAHWEH, the Godname of Chokmah, and 15 is the number of YAH, the shorter version of the Godname. It demonstrates how this well-known Name of God prescribes through its gematria number the yod population of the inner form of the Tree of Life. The number of yods surrounding the 14 centres of the (7+7) enfolded polygons = 87 + 47×3n+1, where 87 is the number value of Levanah, the Mundane Chakra of Yesod.
For reference, Table 5 lists the formulae for the geometrical and yod populations of the nth-order m-gon:
Table 5. Geometrical & yod compositions of the nth-order m-gon.
| Number of corners (including centre of m-gon) |
Cn(m) = 1 + m(1+3n−1)/2 |
| Number of sides |
Sn(m) = m(1+3n)/2 |
| Number of triangles |
Tn(m) = 3n−1m |
| Total number of geometrical elements |
Gn(m) = 1 + m(1+3n) |
| Number of hexagonal yods |
hn(m) = m(1+3n−1+3n) |
| Total number of yods |
Yn(m) = 1 + 3m(1+3n)/2 |
Also for reference, Table 6 lists the formulae for the geometrical and yod populations of the inner Tree of Life composed of nth-order polygons:
Table 6. Geometrical & yod compositions of the 7 enfolded nth-order polygons and the (7+7) enfolded nth-order polygons.
|
7 enfolded polygons |
(7+7) enfolded polygons |
|
| Number of corners (including centres of polygons) |
Cn = ½(35 + 47×3n−1) |
33 + 47×3n−1 |
| Number of sides |
Sn = ½(35 + 47×3n) |
34 + 47×3n |
| Number of triangles |
Tn = 47×3n−1 |
94×3n−1 |
| Total number of geometrical elements |
Gn = 35 + 47×3n |
67 + 94×3n |
| Number of hexagonal yods |
Hn = 35 + 188×3n−1 |
68 + 376×3n−1 |
| Total number of yods |
Yn = ½(105 + 47×3n+1) |
101 + 47×3n+1 |
The number of yods in the (7+7) enfolded polygons outside the root edge = 97 + 47×3n+1, where 47 = 21 + 26 (sum of Godname numbers of first two Sephiroth) and 97 = 21 + 26 + 50 (sum of Godname numbers of first three Sephiroth). The number value of Haniel, the Archangel of Netzach, is 97. The number of yods in the seven enfolded polygons that line the Sn sides of their Tn tetractyses = Yn − Tn = ½(105 + 329×3n−1). The number of yods that line sides of the 2Tn tetractyses in the (7+7) enfolded polygons = 101 + 329×3n−1. 101 is the number value of Michael, the Archangel of Tiphareth, which immediately precedes Netzach. The total number of yods in the (7+7) enfolded polygons = 101 + 47×3n+1.
From the formulae in Table 5, the following relationship between Gn(m) and Yn(m) emerges:
Yn(m) = ½(3Gn(m) −1).
Writing Yn(m) = Ŷn(m) + 1 and Gn(m) = Ĝn(m) + 1, where "1" denotes the centre of the m-gon, the number of yods Ŷn(m) surrounding this centre is related to the number of geometrical elements Ĝn(m) that surround it by:
2Ŷn(m) = 3Ĝn(m) = 3m(1+3n),
i.e., Ŷn(m)/Ĝn(m) = 3/2. This simple result helps to reduce the amount of calculation needed to determine the yod and geometrical populations of polygons of any order, as well as any combination of separate polygons. In particular, the number of yods that surround the centres of the seven types of separate nth-order polygons making up the inner Tree of Life = ∑Ŷn(m) = (3/2)(1+3n)∑m = 72(1+3n) = 72 + 8×3n+2. It means that the number of geometrical elements surrounding the centres = ∑Ĝn(m) = (2/3)×∑Ŷn(m) = (2/3)×(72 + 8×3n+2) = 48 + 16×3n+1. As a check, the number of yods surrounding the centres of the seven separate 1st-order polygons = 72 + 216 = 288, and the number of geometrical elements surrounding them = 48 + 144 = 192, both of which calculations are correct (see the last A columns in Tables 1 & 2).