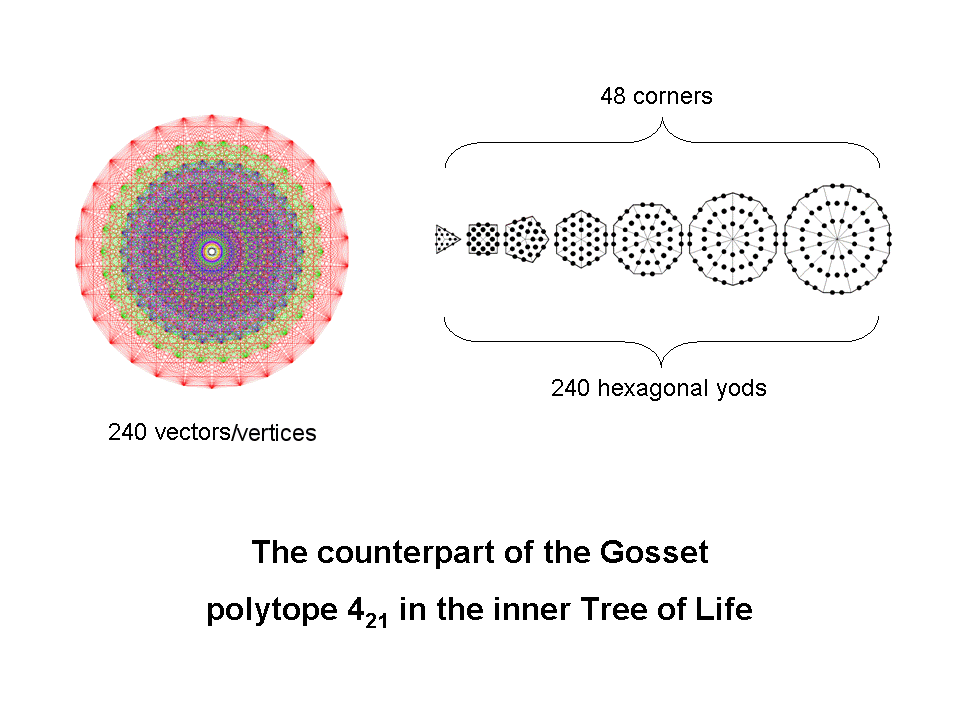

The counterpart in the inner Tree of Life of the 240 vertices of the 8-dimensional Gosset polytope (here is a magnifiable version in PDF format that shows its 6720 edges) are the 240 hexagonal yods in the seven separate, regular, Type A polygons whose 48 sectors are tetractyses. Each hexagonal yod symbolises a vertex of the semi-regular 421 polytope whose position vector in 8-dimensional space is that of one of the 240 roots of E8, the rank-8 exceptional Lie group that appears in E8×E8 heterotic superstring theory.
The Gosset polytope is an 8-dimensional polytope with 240 vertices, 6720 edges, etc (see here). A Type C n-gon has n Type B triangular sectors, the 9 triangles per sector having 14 sides. The number of sides of the (9×48=432) triangles in the 48 Type B sectors of the 7 separate Type C polygons making up the inner Tree of Life = 48×14 = 672. The inner form of 10 Trees of Life consists of 10 sets of 7 polygons. They are composed of (10×432=4320) triangles with (10×672=6720) sides. They are the counterpart of the 6720 edges of the faces of the 421 polytope. As 10 Trees of Life represent a single Tree in a more differentiated form, its inner form manifests as the Gosset polytope, which is, therefore, a holistic system.