|
ARTICLE 50 (Part 2)

by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth.
Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
The polyhedral form of the
Tree of Life is the 144 Polyhedron with 144 faces and the disdyakis
triacontahedron with 120 faces. They are symbolized by the 144 yods
inside the boundaries of the seven, tetractys-constructed, enfolded
polygons of the inner Tree of Life, which are lined by 120 yods. The 74
vertices of the 144 Polyhedron correspond to the 74 yods up to the top
of the lowest Tree of Life that are not Sephiroth. The 62 vertices of
the disdyakis triacontahedron correspond to the 62 corners of the inner
Tree of Life that are unshared with its outer form. The faces of the
rhombic dodecahedron that generate the 144 polyhedron are rhombi with
the proportions of √2:1. The faces of the rhombic triacontahedron that
underlies the disdyakis triacontahedron are Golden Rhombi with the
proportions of the Golden Ratio. Both types of rhombi are implicit in
the geometry of the outer Tree of Life. The Golden Rhombus is implicit
in the Fano plane, which represents the algebra of the octonions. The 60
vertices surrounding an axis passing through two opposite C vertices lie
in 15 sheets. They form 15 polygons which, together with the two C
vertices, have 550 geometrical elements, that is,
10F10
, where
F10 is the
tenth Fibonacci number. The 299 elements in one half of the
polyhedron and the remaining 251 elements are the counterpart of the
299 Sephiroth in the 49-tree that maps the cosmic physical plane and
the 251 Sephiroth in the 42 Trees above it that map the six cosmic
superphysical planes of consciousness. The 550 geometrical elements
(370 vertices & sides, 180 triangles) are the counterpart of the
550 geometrical elements (370 vertices & sides, 180 triangles) in
the 50 faces of the five Platonic solids. The 34
(F9) corners of the 27 sectors
in each set of seven polygons either above or below the central one
correspond to the 34 corners associated with each set of seven
enfolded polygons that are unshared with polygons enfolded in the
next higher Tree. The 34 corners of the 21 triangles in each half of
the two-dimensional Sri Yantra are their counterpart. The ninth Lucas
number 76 is the number of vertices & centres of polygons that
surround the centre of the disdyakis triacontahedron. The tenth Lucas
number 123 is the number of points & lines shaping the 15
polygons. Equivalent to the I Ching table of 64 hexagrams and the
7-tree, the Sri Yantra embodies the superstring structural parameter
1680. This is also embodied in the 21 copies of the first four
Platonic solids that fit the disdyakis triacontahedron. The 28
polyhedra that fit it embody the superstring structural parameter
3360. This is the number of yods in the seven enfolded polygons when
their 47 sectors are 2nd-order tetractyses. F9 is the number of tree levels in the
10-tree, whose 361 sectors of 127 triangles have 550 sides.
Prescribed by ADONAI, the Godname of Malkuth, the 1680 yods below its
top when the sectors of their triangles are tetractyses symbolize the
1680 turns in each of the ten helical, closed curves of the
E8×E8 heterotic
superstring.
|
Page Index
|
Part 1
|
|
|
Part 2
|
|
|
|
Page
|
|
|
Page
|
|
Table of number values of the Sephiroth in the four Worlds
|
|
|
Table of number values of the Sephiroth in the
four Worlds |
|
|
The Tree of Life
|
|
|
Geometrical properties of the 13 Archimedean & 13 Catalan
solids |
|
|
The Upper & Lower Faces of the Tree of Life
|
|
|
The polygonal Tree of Life encodes its polyhedral
counterpart |
|
|
Fibonacci & Lucas numbers
|
|
|
Construction of the polyhedral Tree of Life |
|
|
Fibonacci & Lucas numbers in the 1-, 2- & 3-tree
|
|
|
Isomorphism between the polygonal & polyhedral Trees of
Life |
|
|
The generation of the inner Tree of Life
|
|
|
√2 & Φ determine the polyhedral Tree of
Life |
|
|
The outer & inner Tree of Life
|
|
|
Connection between the Tree of Life and the faces of the
rhombic dodecahedron & rhombic triacontahedron |
|
|
Fibonacci numbers in the geometry of the inner Tree of Life
|
|
|
The Golden Rhombus in the Fano plane |
|
|
Geometrical composition of the outer & inner Tree of Life
|
|
|
The 15 sheets of vertices in the disdyakis
triacontahedron |
|
|
The ninth Fibonacci number in the outer & inner Tree of Life
|
|
|
The disdyakis triacontahedron as the polyhedral representation
of CTOL |
|
|
Fibonacci numbers & the Golden Ratio in the DNA molecule
|
|
|
The 34 corners of the 27 sectors of the seven
polygons |
|
|
Comparison of the 64 codons & 64 anticodons with the 64 hexagrams
|
|
|
The two sets of 7 polygons are analogous to the two halves of
the inner Tree of Life and the trunk and branches of the outer Tree of
Life |
|
|
Comparison of the 384 geometrical elements of the 14 polygons with the 384
lines & broken lines in the 64 hexagrams
|
|
|
The ninth & tenth Lucas numbers determine the 15 sheets of
vertices |
|
|
Comparison of the 64 hexagrams with the Sri Yantra
|
|
|
The disdyakis triacontahedron embodies the fine-structure
number 137 |
|
|
The five Platonic solids as a sequence governed by Fibonacci numbers
|
|
|
The equivalence of the outer Tree of Life and the Sri
Yantra |
|
|
F8, F9 & F10 in the five Platonic
solids
|
|
|
The equivalence of the inner Tree of Life and the Sri
Yantra |
|
|
The first four Platonic solids and the square embody the dimension 248 of
E8
|
|
|
The equivalence of the Sri Yantra and 7 overlapping Trees of
Life |
|
|
How the 1-tree embodies the dimension 248 of E8
|
|
|
The equivalence of the Sri Yantra and the 7-tree |
|
|
How the (7+7) separate polygons of the inner Tree of Life embody
E8×E8
|
|
|
The Sri Yantra embodies the superstring structural parameter
1680 |
|
|
1370 yods on edges of tetractyses in the five Platonic solids
|
|
|
Numbers of hexagonal yods in the faces of the Platonic
solids |
|
|
The inner Tree of Life contains 1370 yods
|
|
|
Correspondence between the outer and inner Trees of
Life |
|
|
Fibonacci, Lucas numbers and the Golden Ratio determine the geometrical
composition of the five Platonic solids
|
|
|
28 polyhedra fit into the disdyakis
triacontahedron |
|
|
The number 247 is a Tree of Life parameter
|
|
|
The faces of the 28 polyhedra have 3360 hexagonal
yods |
|
|
Properties of the five Platonic solids
|
|
|
The seven enfolded polygons of the inner Tree of Life have
3360 yods |
|
|
Counterpart of the internal geometrical composition of the Platonic solids
in the inner Tree of Life
|
|
|
EHYEH prescribes the superstring structural parameter
1680 |
|
|
Counterpart of the internal composition of the Platonic solids in the inner
form of ten Trees of Life
|
|
|
49 overlapping Trees of Life contain 1680 geometrical
elements |
|
|
The 3-tree determined by the tenth Lucas number encodes the human skeleton
|
|
|
1680 geometrical elements surround an axis of the disdyakis
triacontahedron |
|
|
The 3-tree encodes the 361 acupuncture points
|
|
|
The number value of Cholem Yesodoth is 168 |
|
|
The eight Church musical modes
|
|
|
Geometrical composition of the Archimedean & Catalan
solids |
|
|
Tone ratios of the notes in the seven octave species
|
|
|
The Godname ADONAI prescribes the 10-tree |
|
|
The tenth Lucas number is the number of Pythagorean intervals between notes
of the seven musical scales
|
|
|
1680 yods lie below the top of the 10-tree |
|
|
References
|
|
|
The 10-tree has 34 tree levels |
|
|
|
|
|
References |
|
1
|
|
|
SEPHIRAH
|
GODNAME
|
ARCHANGEL
|
ORDER
OF
ANGELS
|
MUNDANE
CHAKRA
|
| 1 |
Kether
(Crown)
620 |
EHYEH
(I am)
21 |
Metatron
(Angel of the
Presence)
314 |
Chaioth ha
Qadesh
(Holy Living
Creatures)
833
|
Rashith ha
Gilgalim
First Swirlings.
(Primum Mobile)
636 |
| 2 |
Chokmah
(Wisdom)
73 |
YAHWEH, YAH
(The Lord)
26,
15
|
Raziel
(Herald of the
Deity)
248 |
Auphanim
(Wheels)
187 |
Masloth
(The Sphere of
the Zodiac)
140 |
| 3 |
Binah
(Understanding)
67 |
ELOHIM
(God in multiplicity)
50
|
Tzaphkiel
(Contemplation
of God)
311
|
Aralim
(Thrones)
282
|
Shabathai
Rest.
(Saturn)
317 |
| |
Daath
(Knowledge)
474 |
|
|
|
|
| 4 |
Chesed
(Mercy)
72 |
EL
(God)
31 |
Tzadkiel
(Benevolence
of God)
62 |
Chasmalim
(Shining Ones)
428
|
Tzadekh
Righteousness.
(Jupiter)
194 |
| 5 |
Geburah
(Severity)
216
|
ELOHA
(The Almighty)
36
|
Samael
(Severity of God)
131
|
Seraphim
(Fiery Serpents)
630
|
Madim
Vehement
Strength.
(Mars)
95 |
| 6 |
Tiphareth
(Beauty)
1081
|
YAHWEH ELOHIM
(God the Creator)
76 |
Michael
(Like unto God)
101
|
Malachim
(Kings)
140
|
Shemesh
The Solar Light.
(Sun)
640 |
| 7 |
Netzach
(Victory)
148
|
YAHWEH SABAOTH
(Lord of Hosts)
129
|
Haniel
(Grace of God)
97 |
Tarshishim or
Elohim
1260
|
Nogah
Glittering
Splendour.
(Venus)
64 |
| 8 |
Hod
(Glory)
15
|
ELOHIM SABAOTH
(God of Hosts)
153
|
Raphael
(Divine
Physician)
311
|
Beni Elohim
(Sons of God)
112
|
Kokab
The Stellar Light.
(Mercury)
48 |
| 9 |
Yesod
(Foundation)
80
|
SHADDAI EL CHAI
(Almighty Living
God)
49,
363
|
Gabriel
(Strong Man of
God)
246
|
Cherubim
(The Strong)
272
|
Levanah
The Lunar Flame.
(Moon)
87 |
| 10 |
Malkuth
(Kingdom)
496
|
ADONAI MELEKH
(The Lord and
King)
65,
155
|
Sandalphon
(Manifest
Messiah)
280 |
Ashim
(Souls of Fire)
351
|
Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168 |
|
|
The
Sephiroth exist in the four
Worlds of Atziluth, Beriah,
Yetzirah and Assiyah.
Corresponding to them are the
Godnames, Archangels, Order of
Angels and Mundane Chakras
(their physical manifestation).
This table gives their number
values obtained by the ancient
practice of gematria, wherein a
number is assigned to each
letter of the alphabet, thereby
giving a number value to a word
that is the sum of the numbers
associated with its letters.
When some of these numbers are
referred to in the article,
they will be written in
boldface.
|
|
|
Figure
2
There are 13
types of semi-regular polyhedra whose faces are two or
more types of regular polygons. They are called the
“Archimedean solids.” Two are chiral, having partners
that are mirror images of them. The dual of a
polyhedron with C vertices and F faces is one with F
vertices and C faces. The duals of the Archimedean
solids are the Catalan solids. Figure 2 displays the numbers of
vertices (C), edges (E) & faces (F) in the 30
Archimedean and Catalan solids, including their
chiral versions. They are listed in order of
increasing numbers of vertices for the Archimedean
solids and increasing numbers of faces for the
Catalan solids. The last of the latter in the list
is the disdyakis triacontahedron, which has
62 vertices, 180 edges & 120
faces. 62 is the number value of
Tzadkiel, the Archangel of
Chesed.
|
|
2
| F |
E |
C |
Archimedean solid |
| 8 |
18 |
12 |
truncated
tetrahedron |
| 14 |
24 |
12 |
cuboctahedron |
| 14 |
36 |
24 |
truncated
cube |
| 14 |
36 |
24 |
truncated
octahedron |
| 26 |
48 |
24 |
rhombicuboctahedron |
| 38 |
60 |
24 |
snub cube |
| 38 |
60 |
24 |
snub cube (chiral
partner) |
| 32 |
60 |
30 |
icosidodecahedron |
| 26 |
72 |
48 |
truncated
cuboctahedron |
| 32 |
90 |
60 |
truncated
icosahedron |
| 32 |
90 |
60 |
truncated
dodecahedron |
| 62 |
120 |
60 |
rhombicosidodecahedron |
| 92 |
150 |
60 |
snub
dodecahedron |
| 92 |
150 |
60 |
snub dodecahedron
(chiral partner) |
| 62 |
180 |
120 |
truncated
icosidodecahedron |
|

|
| Catalan
solid |
F |
E |
C |
| triakis
tetrahedron |
12 |
18 |
8 |
| rhombic
dodecahedron |
12 |
24 |
14 |
| triakis
octahedron |
24 |
36 |
14 |
| tetrakis
hexahedron |
24 |
36 |
14 |
| deltoidal
icositetrahedron |
24 |
48 |
26 |
| pentagonal
icositetrahedron |
24 |
60 |
38 |
pentagonal
icositetrahedron
(chiral partner) |
24 |
60 |
38 |
| rhombic
triacontahedron |
30 |
60 |
32 |
| disdyakis
dodecahedron |
48 |
72 |
26 |
| triakis
icosahedron |
60 |
90 |
32 |
| pentakis
dodecahedron |
60 |
90 |
32 |
| deltoidal
hexacontahedron |
60 |
120 |
62 |
| pentagonal
hexacontahedron |
60 |
150 |
92 |
pentagonal
hexacontahedron
(chiral partner) |
60 |
150 |
92 |
| disdyakis
triacontahedron |
120 |
180 |
62 |
|
|
Figure 3
With their 47 sectors
turned into tetractyses, the seven enfolded polygons making
up half of the inner Tree of Life have 264 yods. 120 yods
line their boundaries, where
120 = 22 +
42 + 62 + 82,
and 144 yods are inside their sides,
where
|
144 = |
10
20
30 40
11
21 31
41
12
22 32
42
13
23 33
43. |
Suppose that two
polyhedral counterparts of the inner Tree of Life exist
and that these two sets of yods symbolise their
vertices or faces. According to Fig. 2, there are no two solids with
144 and 120 vertices. The truncated
icosidodecahedron has 120 vertices, but none of
these polyhedra has 144 vertices. Nor can such a
polyhedron be created by sticking tetrahedra or
pyramids onto faces of any Archimedean or Catalan
solid. For that to be possible, C + F = 144, but
none of them has this property. However, the
disdyakis triacontahedron has 120 faces and sticking
tetrahedra onto the 48 faces of the
disdyakis dodecahedron generates a polyhedron with
144 faces. This allows the 120 yods on edges of the
seven enfolded polygons to be interpreted as
denoting the 120 faces of the last Catalan solid and
the 144 internal yods as symbolizing the 144 faces
of a polyhedron (hereafter called the “144
Polyhedron”).
|
|
3
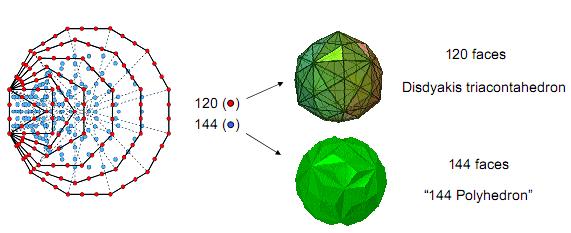
The 120 red yods on the boundaries
of the seven enfolded polygons symbolize the 120 faces of the disdyakis
triacontahedron with 62 vertices. Their 144 internal, blue yods
symbolize the 144 faces of a polyhedron with 74 vertices.
|
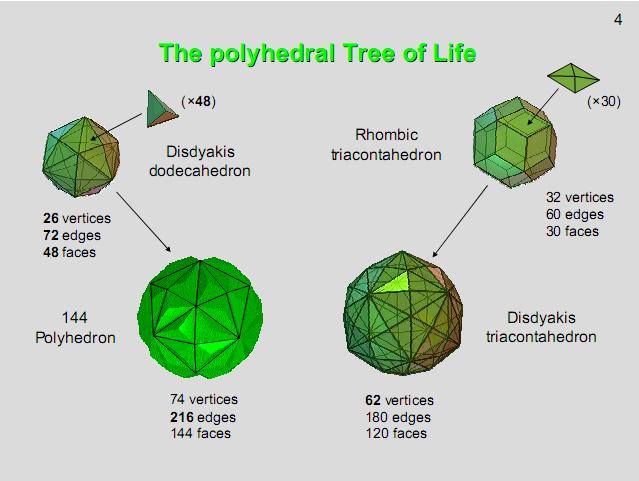
Figure 4
The Catalan solid
called the disdyakis dodecahedron has 26
vertices, 72 edges & 48 faces.
Attaching tetrahedra to each face generates the 144
Polyhedron with (26+48=74) vertices,
(72+3×48=216) edges and
(3×48=144)
triangular faces. 144 is
F12, the twelfth Fibonacci number. 72
is the number value of Chesed, the first Sephirah of
Construction and 216 is the number value of
Geburah, the second Sephirah of Construction opposite
it in the Tree of Life.
The Catalan solid
called the rhombic triacontahedron has 32 vertices, 60
edges & 30 so-called “Golden Rhombic” faces (to be
described in Fig. 6). Attaching four-faced
pyramids with Golden Rhombic bases to their faces
generates the disdyakis triacontahedron with (32+30)
vertices, (60+4×30=180) edges and (4×30=120)
triangular faces.
The 144
Polyhedron and the disdyakis triacontahedron constitute
the polyhedral form of the Tree of Life. They represent
the union of, respectively, the Yang (male) and Yin
(female) aspects of Divine Unity.
|
|
|
Figure 5
Imagine a set of
overlapping Trees of Life with their triangles turned
into tetractyses. Of the 84 yods up to the level of the
top of the lowest Tree, ten are Sephiroth of that Tree,
so that 74 more yods are needed to complete it. There
are 26 yods down to the level of
Daath, leaving 48 yods. 26 is the number
value of YAHWEH, the Godname of Chokmah and
48 is the number value of
Kokab, the Mundane Chakra of Hod. The 74 yods
other than Sephiroth symbolise the 74 vertices of the
144 Polyhedron, the 26 yods denoting the
26 vertices of the underlying disdyakis
dodecahedron and the 48 yods denoting
the 48 vertices added by attaching
tetrahedra to its 48 faces.
When this Tree is
projected onto the plane of the 14 polygons of the
inner Tree of Life, seven Sephiroth and Daath coincide
with some of the 70 corners of the polygons, leaving
62 corners that are intrinsic to them,
being unshared with the projected outer Tree of Life.
They denote the 62 vertices of the
disdyakis triacontahedron. The 144 Polyhedron is the
polyhedral version of the outer Tree of Life and the
disdyakis triacontahedron is the polyhedral form of the
inner Tree of Life. The 30 peaks of the Golden Rhombic
pyramids in the disdyakis triacontahedron (called “A”
vertices) correspond to the 30 yellow corners of the
pentagons, hexagons & dodecagons. The 12 B vertices
(vertices of an icosahedron) correspond to the 12 blue
corners of the two octagons. The 20 C vertices
(vertices of a dodecahedron) correspond to the 20 red
corners of the squares & decagons.
|
|
5
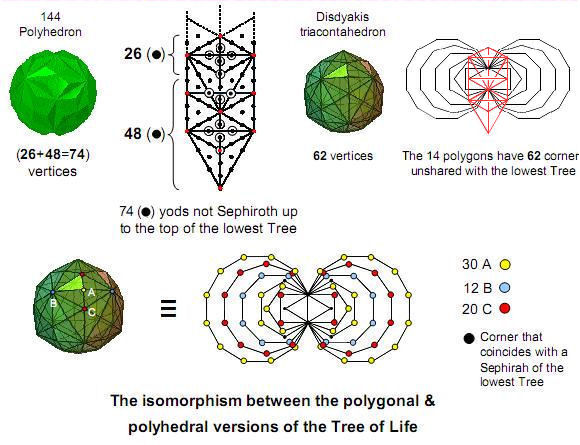
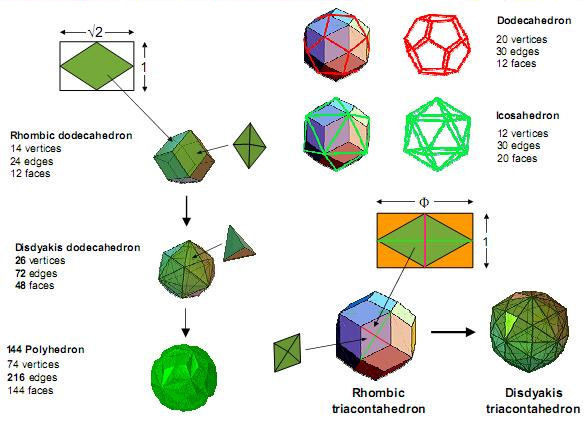
Figure 6
The 12 faces
of a rhombic dodecahedron are rhombi whose
diagonals have lengths in the proportion of
√2:1. Attaching rhombic pyramids to their faces
creates the disdyakis dodecahedron with
48
faces.
Attaching tetrahedra to the latter generates the
144 Polyhedron with 144
faces.
144
is the
twelfth Fibonacci number. It is
also 122. The
geometrical meaning of this is that each of the
12 faces of the rhombic dodecahedron generates
12 faces of the 144 Polyhedron.
The rhombic
triacontahedron has the 32 vertices of the
underlying dodecahedron and icosahedron. The
diagonals of its faces are their edges, the
shorter (red) one being the edge of the former
and the longer (green) one being the edge of the
latter. The ratio of their lengths is the Golden
Ratio Φ. Sticking
Golden Rhombic pyramids onto the 30 faces of the
rhombic triacontahedron creates the disdyakis
triacontahedron. Whereas the Golden Ratio is
only implicit in the geometry of the pentagonal
faces of the dodecahedron, it becomes explicit
in the proportions of the diamond-shaped bases
of the 30 pyramids. The ideal of proportion is
realised in the polyhedral Tree of
Life.
|
|
6
The longer diagonal of the rhombic face of the
rhombic dodecahedron is the edge of a cube. Its
shorter diagonal is the edge of an octahedron. The
ratio of their lengths is √2
= 1.414… . These Platonic solids are dual to each
other. The two other Platonic solids that are dual
to each other — the icosahedron and the
dodecahedron — share an analogous property in that
their edges are, respectively, the longer and
shorter diagonals of the rhombic faces of the
rhombic triacontahedron. Their ratio is the Golden
Ratio
Φ
= 1.618… . These rhombi are generated in a simple
way by the geometry of the outer Tree of Life.
Fig.
7 shows that the ten Sephiroth are
the centres or points of intersection of a
column of white circles. Let us take their radii
as one unit. The central Pillar of Equilibrium
intersects the path joining Chesed and Geburah
at a point A that is one unit away from the
vertical right-hand tangent BC to these circles.
ABCD is a square with sides of length 1.
Therefore, its diagonal AC = √(12 +
12)
=
√2
. With A as centre, draw a circle passing
through C of radius √2 (shown as a dashed
line). It intersects the line drawn along AB at
E. E′ i
s the corresponding point on the other side of the
central pillar. EE' = 2√2. The central pillar
intersects the path joining Netzach and Geburah at
D'. DD' = 2. Therefore, EE'/DD' =
2√2/2 = √2. We find that the
rhombus DED'E' has the same shape as the
rhombic face of the rhombic
dodecahedron.
Extend the tangent at B to the point F, where BC =
CF = 1. Then, BF = 2 and AF
= √(
22
+ 12)
= √5.
The line AF intersects CD at G, where AG = GF =
√5/2.
With G as centre, draw a circle of radius ½. It
intersects AF at H, where AH = √5/2
+ ½ = (√5
+1)/2. This is Φ,
the Golden Ratio. With A as centre, draw a circle
of radius AH. It intersects the extension of AB at
I, where AI = Φ.
I' is its counterpart on the other side of
the central pillar. II' = 2Φ.
Therefore, II'/DD' = 2Φ/2
= Φ.
The rhombus DI D'I' has the same shape as the
rhombic face of the rhombic triacontahedron. What
manifests finally as the fruit of the Tree of Life,
namely, the disdyakis triacontahedron with golden
rhombic faces, was within it as their seed shape
from the very beginning!
|
|
7
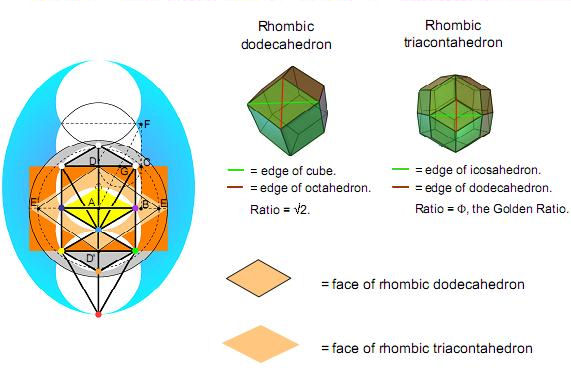
The geometry of the Tree of Life
generates the rhombic faces of the rhombic dodecahedron & rhombic
triacontahedron.
Figure 8
The Fano plane is
known to mathematicians as the simplest projective
plane. It has seven points and seven lines (three
sides and three internal diagonals of a triangle and
the circle inscribed in it). The Golden Rhombus is
implicit in its geometry. The Fano plane, which
represents the algebra of the octonions, has
the 168
symmetries of the
symmetry group SL(3,2), which is the symmetry group
of G2, the rank-2 exceptional group. This
is the symmetry group of the octonions. SL(3,2) is
isomorphic to PSL(2,7), the symmetry group of the
Klein quartic:
X3Y +
Y3Z + Z3X = 0.
Given that its
dimension is 168
, can
it be just coincidental that the disdyakis
triacontahedron, whose groups of four faces have the
outline of a Golden Rhombus, have 1680 vertices,
lines & triangles surrounding an axis joining
two opposite vertices when its interior triangles
are divided into their sectors (1)? This number is
the number of circularly polarised oscillations in
each of the ten closed curves making up the
E8×E8 heterotic superstring,
as described by the Theosophists Annie Besant &
C.W. Leadbeater over a century ago (2). It prove
that the helical structure of the basic unit of
matter is embodied in the geometrical composition of
the polyhedral Tree of Life blueprint.
|
|
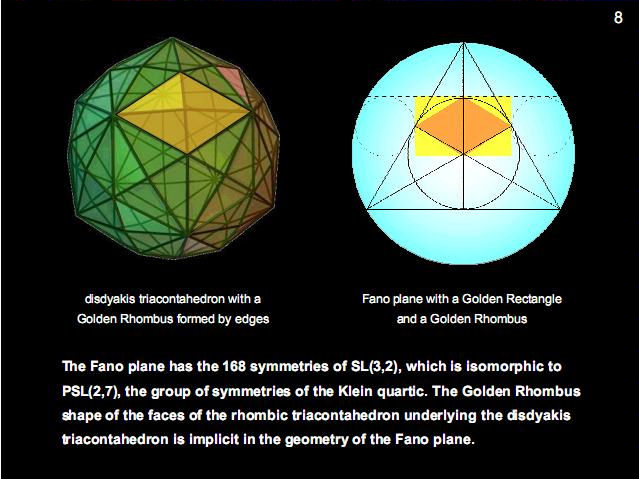
Figure 9
Consider a
straight line passing through two opposite C
vertices of the disdyakis triacontahedron. The 60
vertices surrounding this axis are grouped
into 15
sheets. Seven
sheets (coloured with the seven colours of the
rainbow) are above the central one (coloured khaki)
and seven sheets are below it. Projected onto the
plane containing the central sheet, the vertices
form triangles and six-sided polygons that are
irregular except for the central one, which is
hexagonal. The rectangular coordinates of the
62
vertices are
arranged according their height (Z' coordinate)
measured along the axis. The vertices in a sheet of
a given colour have the same height. The numbers
between the arrows indicate the numbers of vertices
in each sheet. Vertices 4 and 59 in the white rows
are the diametrically opposite C vertices through
which the axis passes. The pattern of
31
vertices below
the thick black line is the mirror image of the
pattern of
31 vertices above
it. 31
is the
number value of EL, the Godname of Chesed.
62
is the
number value of Tzadkiel
, its
Archangel. For more details see Article 36
(3).
|
|
9
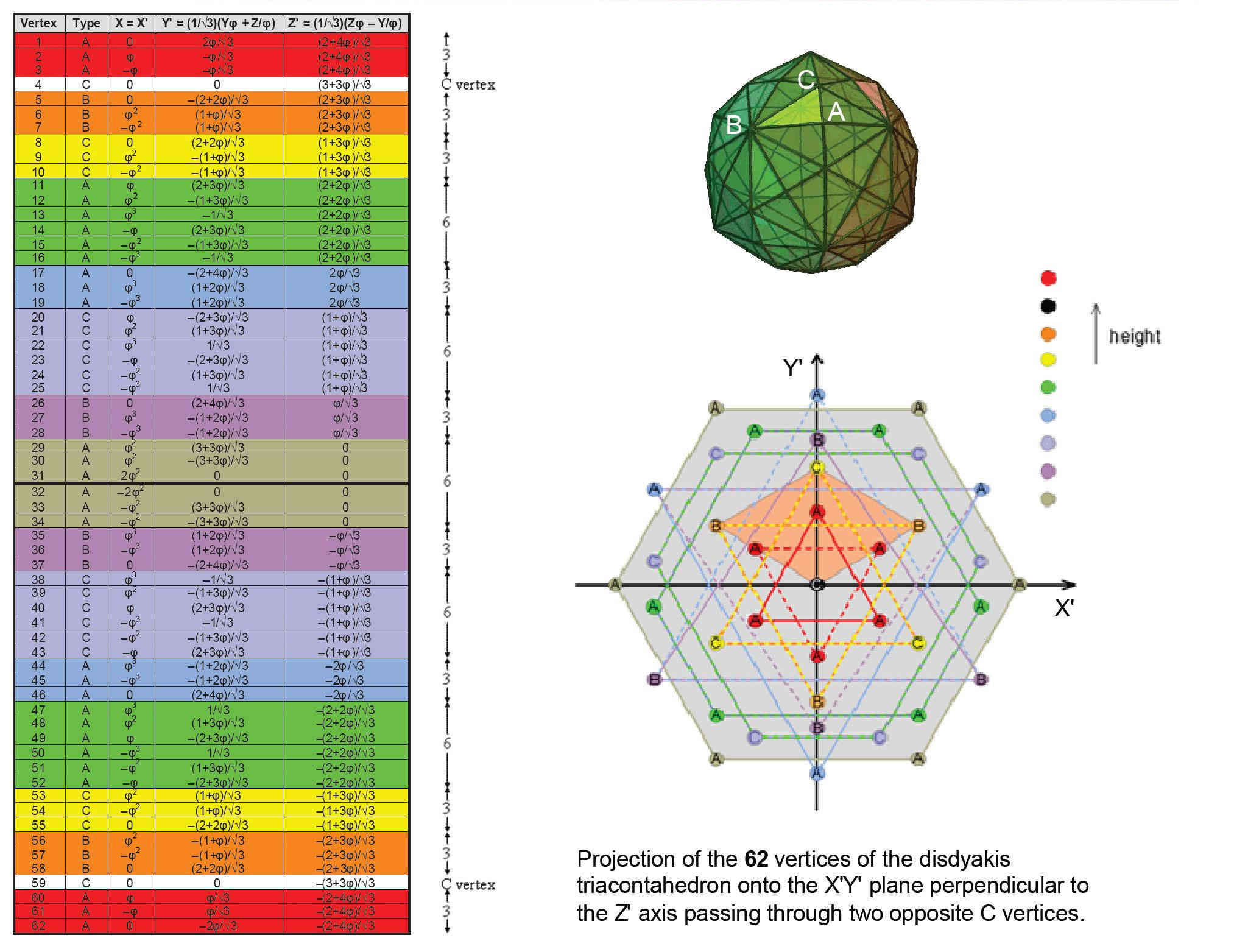
Figure 10
Sacred geometries
are maps of all levels of physical and superphysical
realities (4). In particular, their Tree of Life
representation is called the "Cosmic Tree of Life"
(CTOL). It consists of 91 overlapping Trees of Life
with 550 Sephirothic levels (SLs), where 550 =
10×55
and
55
is
the tenth Fibonacci number. We saw in Part 1 that
this is the number of corners, sides and triangles
in the 50
faces
of the five Platonic solids (see Fig. 16 and its commentary). There
are 299 SLs up to the top of the lowest
49
Trees
of Life ("49-tree”) and 251
SLs above it. The
49-tree maps
the 49
subplanes of the
seven planes of consciousness taught in Theosophy.
Above it are the 42 Trees of Life mapping the 42
subplanes of the six cosmic superphysical
planes.
Suppose that
the 15
polygons formed
by the 60 vertices surrounding an axis passing
through two opposite C vertices are divided into
their sectors. Then suppose that each of the 60
sectors is again divided into its three sectors.
Inspection of the projection of vertices onto the
central sheet shows that none of the sides of the
polygons is an edge of the disdyakis
triacontahedron. If one imagines all the vertices
joined to the centre so as to form triangles with
polyhedral edges as one side, the central hexagon is
the only polygon whose internal sides of sectors
coincide with these triangles. They are coloured red
in Fig. 10. The two C vertices on the
axis are unshared with the 15
polygons. Listed
in the table are the numbers of points, lines &
triangles making up the polygons (including these
two vertices) that are unshared (the centre of the
central hexagon is shared with internal triangles of
the polyhedron and so is not included in the
numbers). The lower half of the disdyakis
triacontahedron has eight polygons with 299 unshared
geometrical elements (including the lower C vertex).
They correspond to the 299 SLs in
the 49-tree. The seven
polygons and the upper C vertex comprise 251
geometrical elements. They correspond to the 251 SLs
above the 49-tree.
CTOL
is encoded in the geometry of the polygons formed by
the vertices of the disdyakis triacontahedron. To
every one of the 550 geometrical elements there
corresponds an SL.
There are
76
points (60 points
surrounding the axis, 14 centres & two C
vertices). This is the ninth Lucas
number L9. 76
is
the number value of YAHWEH ELOHIM, the Godname of
Tiphareth. There are 370 unshared vertices &
sides of 180 triangles. Compare this with the 370
vertices & sides of the 180 triangles in the
faces of the five Platonic solids (see Fig. 16). The holistic parameter 550
divides in exactly the same way! There are
474
sides
& triangles. 474
is
the number value of Daath (“knowledge”). Truly, the
number 550 measures the knowledge of YAHWEH ELOHIM
(“God the Creator”), being the number of SLs in
CTOL.
|
|
Figure 11
The seven
polygons above or below the central sheet of
vertices in the disdyakis triacontahedron have 27
sectors with 34
corners.
34
is
the ninth Fibonacci
number F9. Dividing each
sector into three triangles and adding the C vertex
associated with them generates
55
vertices other
than centres of polygons, where
55
is the tenth Fibonacci number
F10.
The two sets of
seven polygons above and below the central sheet
have 54 sectors with (2×34
=68)
corners. This is the counterpart of the 68 corners
per set of (7+7) polygons enfolded in each
overlapping Tree of Life, 34
corners per set
of seven polygons (see Fig. 10, Part 1). This
property serves to illustrate that the disdyakis
triacontahedron is the polyhedral counterpart of the
inner Tree of Life, as has been shown in many
previous articles.
|
|
11
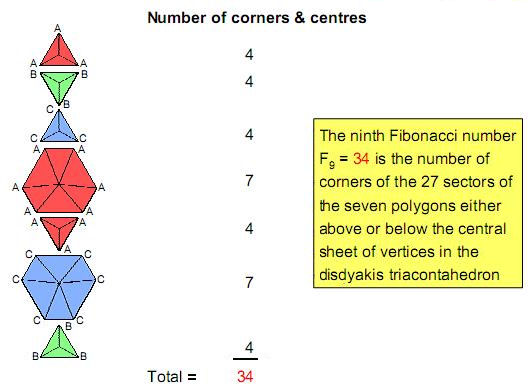
|
Figure 12
Another
counterpart of the disdyakis triacontahedron to the
inner Tree of Life is as follows: associated with
each set of seven enfolded polygons are their 35
corners (34
outside their
shared root edge and one corner that is an endpoint
of the latter). The 27 sectors of each set of seven
polygons in the disdyakis triacontahedron
have 34
corners.
Including the single C vertex on the axis that is
associated with each set, there are 70 vertices and
centres surrounding the central polygon, 35 per set
of seven polygons & C vertex).
The trunk of the
outer Tree of Life is:
Point (Kether)
Line (Path joining Chokmah &
Binah)
Triangle (triangle
with corners at Chesed, Geburah &
Tiphareth)
Tetrahedron
(tetrahedron with vertices at Netzach, Hod, Yesod &
Malkuth).
Constructed from
tetractyses, they have 35 yods. The branches of the
Tree of Life are its geometrical components outside its
trunk. They, too contain 35 yods. This 35:35 division
is characteristic of holistic systems. It is displayed
by the 14 polygons and the two C vertices. The latter
correspond to the two endpoints of the root edge — the
start and end of the unfolding of the polygonal
geometry of the inner Tree of Life.
|
|
12
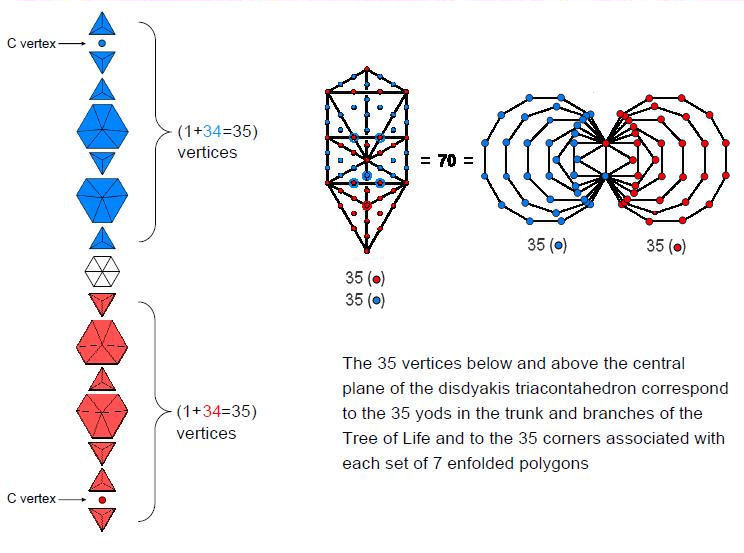
|
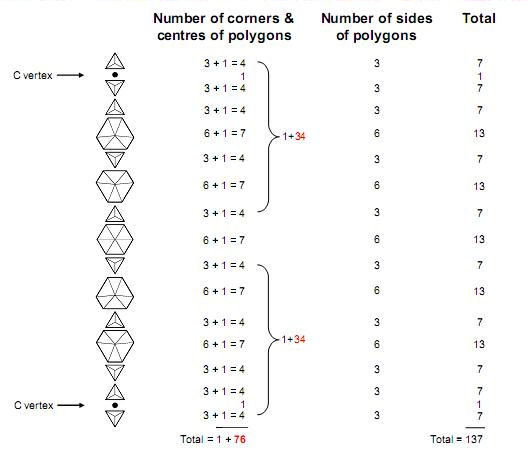
Figure 13
Each set of
seven polygons has 27 corners that are vertices
of the disdyakis triacontahedron. Its centre and
the 54 vertices of both sets creates a set
of 55
points. This
number is F10. Each set has 27 sides.
Including either the six corners of the central
hexagon and a C vertex on the axis or the six
sides of the hexagon and the other C vertex
creates two sets of 34
points &
sides, where 34
is the ninth
Fibonacci number F9. The number of
points & lines forming the shapes of
the 15
polygons
= 55
+
2×34
= 123. This is
the tenth Lucas number L10. The
polygons constitute a geometrical realisation
for n = 10 of the general relation between
Lucas numbers and Fibonacci
numbers:
Ln
= Fn + 2Fn-1
as
L10 = F10 +
2F9. The factor of 2 refers to the
upper and lower halves of the polyhedron, each
containing seven polygons.
This property
is the polyhedral counterpart of the
123
geometrical
elements in the 3-tree (Fig. 5, Part 1), which
has 55
geometrical
elements in the lowest Tree of Life and
34
elements in
each of the second and third Trees.
76
polyhedral
vertices & centres of the 14 polygons
surround the centre of the disdyakis
triacontahedron. 76
is the ninth
Lucas number L9.
|
|
13
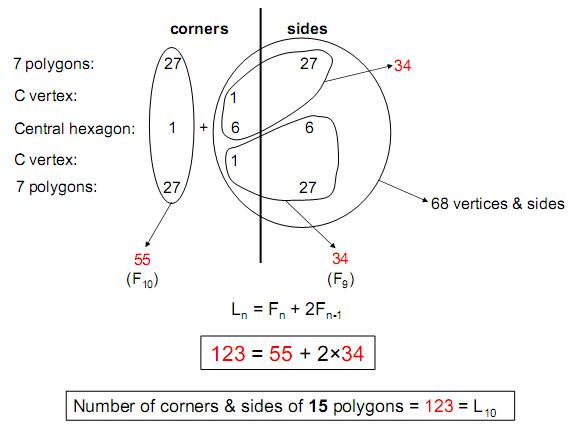
|
Figure 14
There are 137
corners & sides in the set of
15
polygons and
the two diametrically opposite C vertices that
form the axis of the disdyakis triacontahedron.
This is the single polyhedral counterpart to the
1370 yods in the inner Tree of Life (Fig. 21,
Part 1) when its 94 sectors are each divided
into three triangles which are then turned into
tetractyses. The number 137 determining the
fine-structure constant α = e2/ħc is
embodied in the arrangement of the vertices of
the disdyakis triacontahedron. It is determined
by the tenth Lucas number L10
= 123,
which is the
number of corners & sides other than the
centres of the 14 polygons above and below the
centre of the polyhedron:
137 =
123
+
14.
It is also
determined by the ninth Lucas number
L9 = 76
because
76
corners/vertices
surround the centre of the
polyhedron:
137 =
76
+
60,
where 60 is
the number of sides of the 15
polygons.
76
is the number
value of YAHWEH ELOHIM, the Godname of
Tiphareth.
The number
137 is embodied in the polyhedral Tree of Life
as the 137 corners of the 396 internal triangles
of the concentric 144 Polyhedron with 74
vertices and the disdyakis triacontahedron
with
62 vertices:
137 = 1 + 74
+ 62
.
|
|
14
|
Figure 15
The 42
triangles surrounding the central triangle in
the 2-dimensional Sri Yantra have 68 corners
(34
corners in
each half). This leaves one other corner of the
central, downward-pointing triangle and the
bindu point in its middle. The 70 points
creating the form of the 2-dimensional Sri
Yantra are the counterpart of the 70 yods in the
outer Tree of Life when its 16 triangles are
tetractyses and the 70 corners of its polygonal,
inner form. It demonstrates the equivalence of
these sacred geometries. The two sets of
34
corners
correspond to the 34
corners of
the 27 sectors of each set of seven polygons
(Fig. 11), whilst the bindu and
lower corner of the central triangle correspond
to the two C vertices on the central axis of the
disdyakis triacontahedron and to the two
endpoints of the root edge shared by the 14
polygons of the inner Tree of Life. Their
counterpart in the outer Tree are its top
(Kether) and bottom (Malkuth). More details
about the analogous features of the Sri Yantra
and other holistic systems are discussed in
Article 35.
|
|
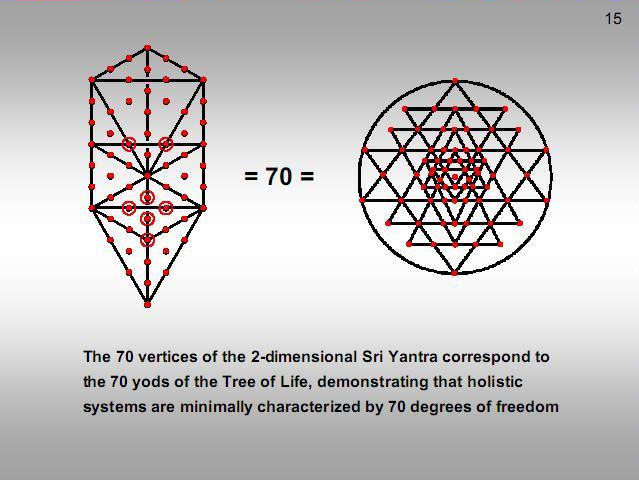
|
Figure 16
The
3-dimensional Sri Yantra is also equivalent to
the inner Tree of Life. As the bindu point is no
longer in the plane of the central triangle, as
in the 2-dimensional case, the latter
constitutes a distinct geometrical element. The
eight geometrical elements making up the central
triangle and bindu correspond to the eight
points that are either corners of the polygons
that coincide with Sephiroth of the outer Tree
when it is projected onto the plane containing
the polygons or centres of polygons. The four
sets of triangles have 252 geometrical elements.
They correspond to the 252 other yods outside
the root edge that make up the
47
tetractyses.
YAHWEH, the Godname of Chokmah with number
value
26, prescribes
both the geometrical composition of the Sri Yantra
and the yod population of the inner Tree of
Life.
|
|
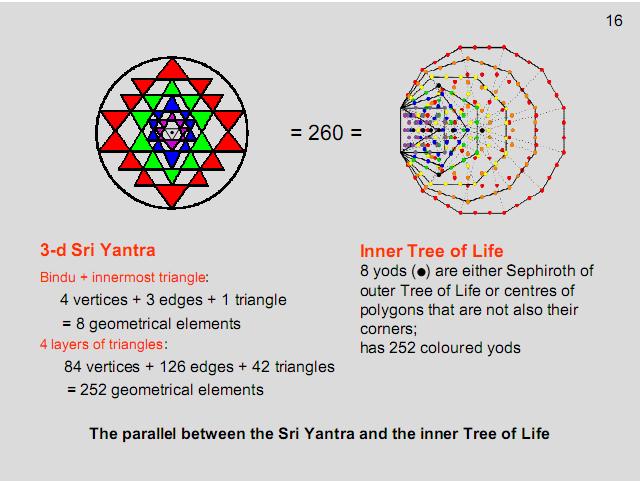
|
Figure 17
The 252
geometrical elements making up the 42 triangles
of the Sri Yantra that surround its central one
correspond to the 252 geometrical elements
composing seven overlapping Trees of Life. The
seven elements in the central triangle that
surround the bindu correspond to the seven
elements (one point, three lines & three
triangles) that are added when the seven Trees
become the 7-tree.
The seven Trees
of Life represent the seven planes of consciousness
corresponding to the seven Sephiroth of
Construction.
|
|
17
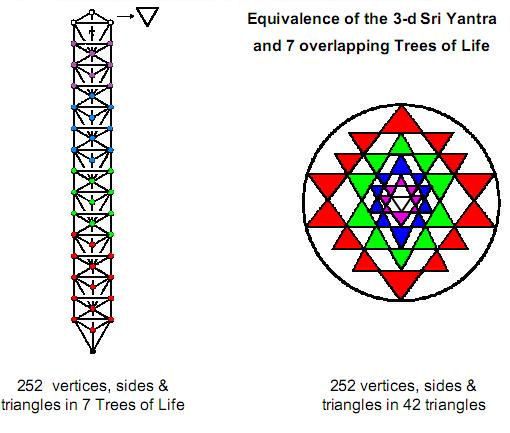
|
Figure 18
Remarkable
confirmation of the equivalence of seven
Trees of Life and the Sri Yantra is provided
by their yod populations when their
triangles are tetractyses. There are 384
yods up to the top of the seventh Tree of
Life in a set of n overlapping Trees
(n>7) and 384 yods that belong either to
the central triangle as hexagonal yods or to
the 42 triangles surrounding it.
|
|
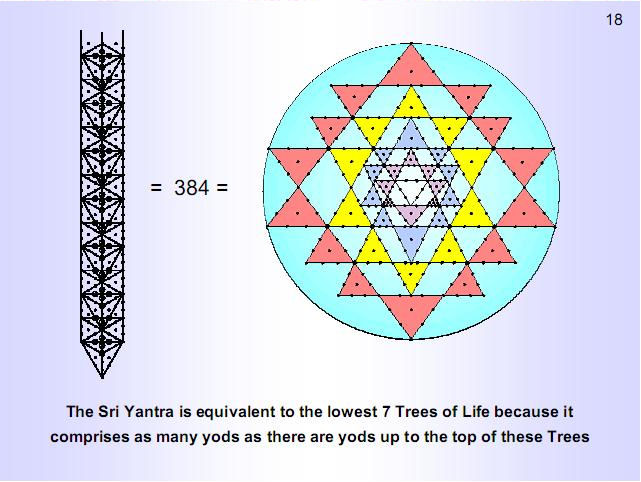
|
Figure 19
The nine
parent triangles that create the Sri Yantra have
27 corners. 26
of them
(denoted by small circles) are corners of the 42
triangles that surround its centre. A Type B
triangle is a triangle whose sectors are each
divided into three sectors. It has 46 yods when
the nine sectors are tetractyses. The 42
triangles has (4×42=168
)
internal corners of their (9×42=378)
tetractyses. 168
is the number
value of the Mundane Chakra of Malkuth. Many
previous articles demonstrated that it is a
structural parameter of the superstring. The 42
Type B triangles surrounding the centre of the
Sri Yantra have 1680 yods other than the
26
corners that
belong to the nine primary triangles and
the 168
internal
corners of tetractyses. This is how the Sri
Yantra embodies the number 1680, recorded over a
century ago by the Theosophist C.W. Leadbeater
as the number of turns in each helical whorl of
the particle that he claimed through his
remote-viewing ability was the basic unit of
matter. The sceptic may argue that the choice of
yods is ad hoc and made to deliver the
number 1680. This ignores the fact that the
corners of tetractyses that are left out of the
calculation number 168 —
the very
superstring structural parameter that numerous
articles have proved is embodied in holistic
systems. The sceptic’s assumption that this,
too, occurs by chance is implausible, especially
given the fact that there are
168
yods
lining the sides of the 21
triangles
in each half of the Sri Yantra, another
occurrence of this number which he must also
regard as coincidental.
|
|
19
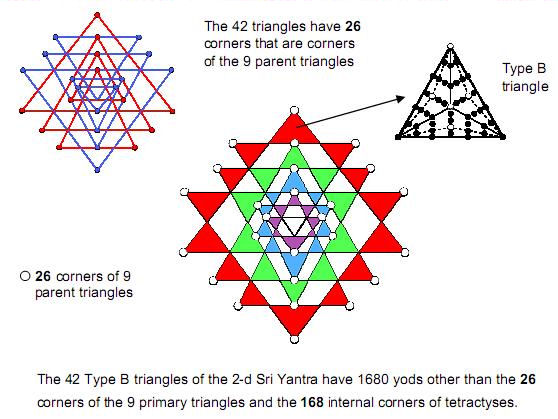
|
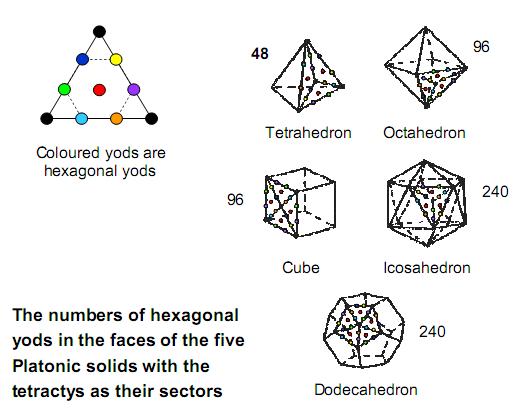
Figure 20
Imagine
the 50
faces of the
five Platonic solids divided into their 180
sectors. Then suppose that each sector is a
tetractys. There are 48
hexagonal
yods in the 12 tetractyses forming the four
faces of the tetrahedron, 96 hexagonal yods in
the eight faces of the octahedron, 96 hexagonal
yods in the six faces of the cube, 240 hexagonal
yods in the 12 faces of the icosahedron &
240 hexagonal yods in the 12 faces of the
dodecahedron. 48
is the number
value of Kokab
,
the Mundane Chakra of Malkuth. The four Platonic
solids associated by the ancient Greeks with the
four Elements of Earth, Water, Air & Fire
have 480 hexagonal yods (240 hexagonal yods in
the tetrahedron, octahedron & cube and 240
hexagonal yods in the icosahedron).
|
|
20
|
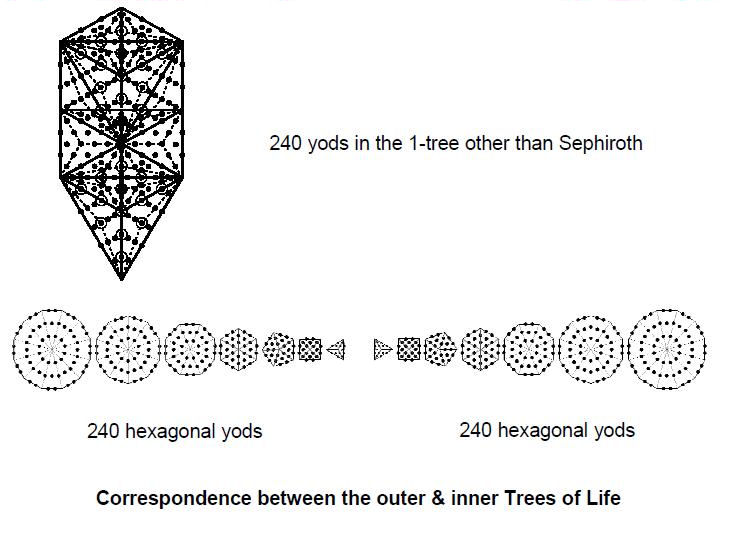
Figure 21
The
counterpart of this property in the outer Tree
of Life are the 240 yods added
to the lowest
Tree when the sectors of its 19 triangles are
turned into tetractyses. Its counterpart in the
inner form of the Tree of Life are the 240
hexagonal yods that are added to each set of
seven separate polygons when their sectors are
turned into tetractyses. Each hexagonal yod
symbolizes one of the 240 roots of the rank-8,
exceptional Lie group E8,
the
(240+240=480) hexagonal yods in the two sets
denoting the 480 roots
of E8×E8,
which is the
symmetry group of the unified interaction of one
of the two types of heterotic
superstring.
|
|
21
|
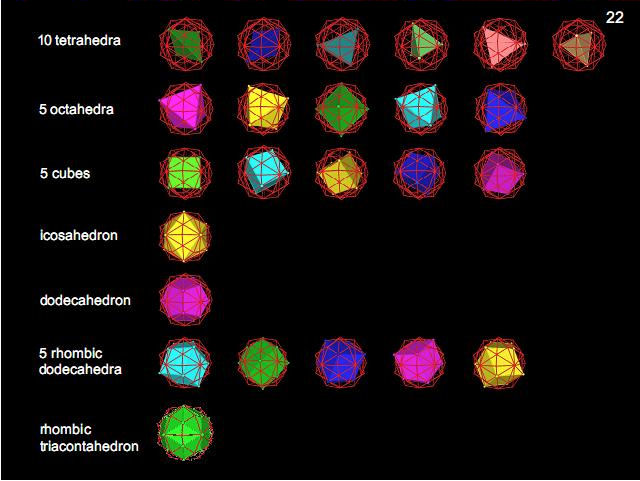
Figure 22
The
62
vertices of
the disdyakis triacontahedron are the vertices
of 28 Platonic & Catalan solids.
21
polyhedra are
copies of the first four Platonic solids. The
seven other polyhedra that can be fitted into
the disdyakis triacontahedron comprise the
dodecahedron, five rhombic dodecahedra and one
rhombic triacontahedron.
|
|
|
Figure 23
Suppose that
the faces of the 28 Platonic & Catalan
solids formed by vertices of the disdyakis
triacontahedron are constructed from
tetractyses. There are 1680 hexagonal yods in
the faces of the 21
copies of the
first four Platonic solids and 1680 hexagonal
yods in the faces of the other seven polyhedra.
The 28 polyhedra therefore have 3360 hexagonal
yods
|
|
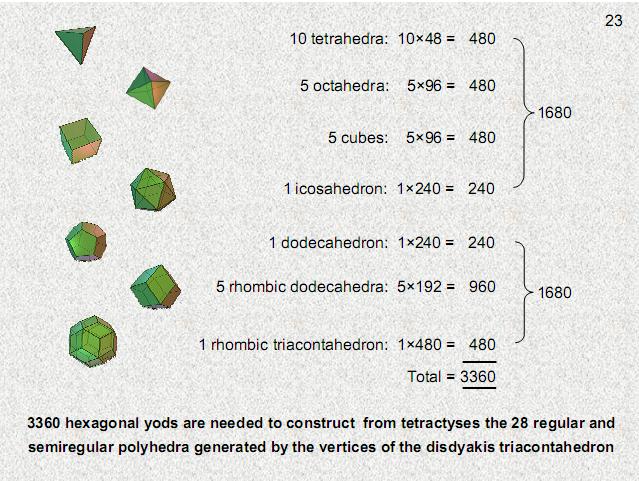
|
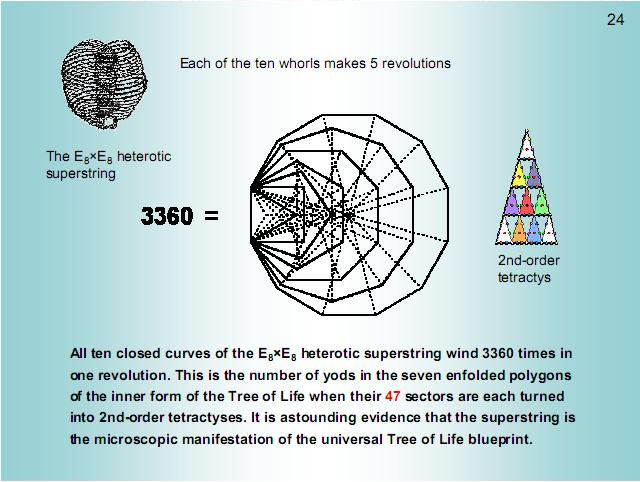
Figure 24
The number
3360 is embodied in the inner Tree of Life as
the 3360 yods in its seven enfolded polygons
when their 47
sectors are
each turned into the so-called ‘2nd-order
tetractys.’ 47
is the eight
Lucas number L8. This is generated
from the Pythagorean tetractys (the 1st-order
tetractys) by regarding each of its ten points
as a tetractys. This higher-order tetractys has
85 yods, where
85 =
40 + 41 + 42 +
43.
84 yods surround
its centre, where
84 =
12 + 32 + 52 +
72.
As a
parameter of all holistic systems, the number
3360 has the following significance for the
structure of the superstring: each of the ten
whorls of the unit of matter described by the
Theosophists Annie Besant & C.W. Leadbeater
is a helix with 1680 turns. It twists five times
around the spin axis of the particle, so that it
winds (1680/5=336) times in one revolution. The
ten whorls wind 3360 times in one revolution and
1680 times in a half-revolution. The
21
copies of the
first four Platonic solids and the seven other
polyhedra embody the number of circularly
polarised oscillations in the ten whorls as they
make these two half-revolutions.
|
|
|
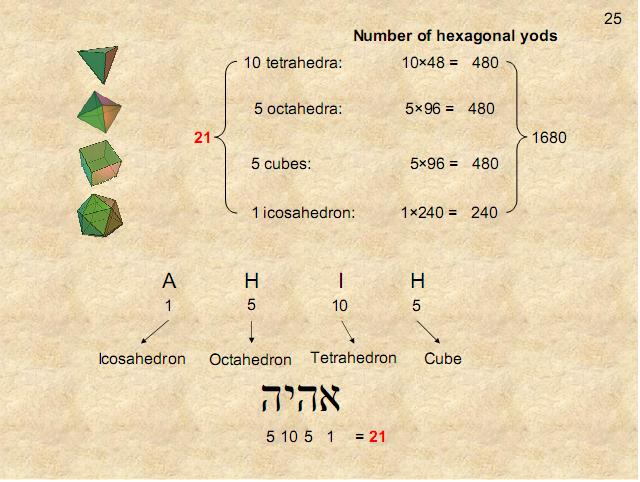
Figure 25
The numbers
of Platonic solids of the first four types that
can be fitted into the disdyakis triacontahedron
and which have 1680 hexagonal yods in their
faces are the letter values of EYHEH (“I am”),
the Godname of Kether, whose number value is
21.
It is also
the eighth Fibonacci
number F8.
This
one of the ways in which this Godname
prescribes the superstring structural
parameter 1680.
|
|
|
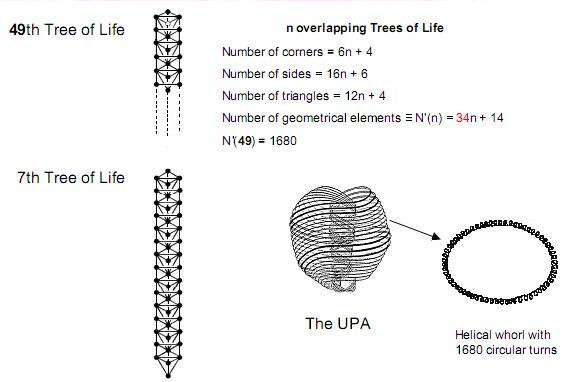
Figure 26
The
number 168
is the
number value of Cholem
Yesodoth, the
Mundane Chakra of Malkuth. Confirmation that
it refers to the Malkuth aspect of the Tree
of Life is the remarkable fact that
49
overlapping
Trees of Life have 1680 corners, sides &
triangles. The lowest 49
Trees in
CTOL map the 49
subplanes
of the cosmic physical plane. Each cosmic
plane corresponds to a Sephirah of
Construction, and the cosmic physical plane
corresponds to Malkuth, the physical level
of CTOL in a cosmic
sense.
49
is the
number value of EL CHAI, the Godname of
Yesod.
|
|
26
|
Figure 27
Joining
the
62 vertices of
the disdyakis triacontahedron to its centre
creates 180 triangles in its interior with
(180×3=540) sectors. There are 60 vertices
surrounding an axis drawn through any two
opposite vertices. The sectors of the internal
triangles have 180 internal corners and (60 +
3×180 = 600) internal sides surrounding the
centre of the polyhedron. Its 120 faces are 120
triangles with 180 sides and 60 corners
surrounding the axis. 1680 corners/vertices,
sides/edges & triangles surround this axis.
The disdyakis triacontahedron embodies the
superstring structural parameter 1680. Its 900
triangles have 780 corners &
sides.
|
|
27
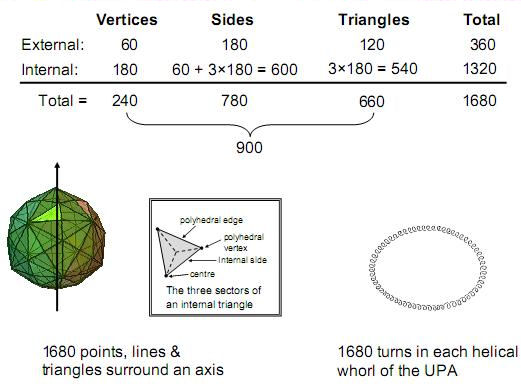
Figure 28
The 1680
geometrical elements that surround any axis
of the disdyakis triacontahedron is the
polyhedral realisation of the number
value 168
of
Cholem
Yesodoth, the
Mundane Chakra of Malkuth. That this is no
coincidence is indicated by the fact that
the 780:900 division of geometrical elements
reflects, apart from the Tree of
Life/tetractys factor of 10, the gematria
number values of both Cholem
(78)
and
Yesodoth (90). In
accordance with the rules of gematria, the
letter value 400 of tav, the final Hebrew
letter in Yesodoth
, can be
contracted to 4.
|
|
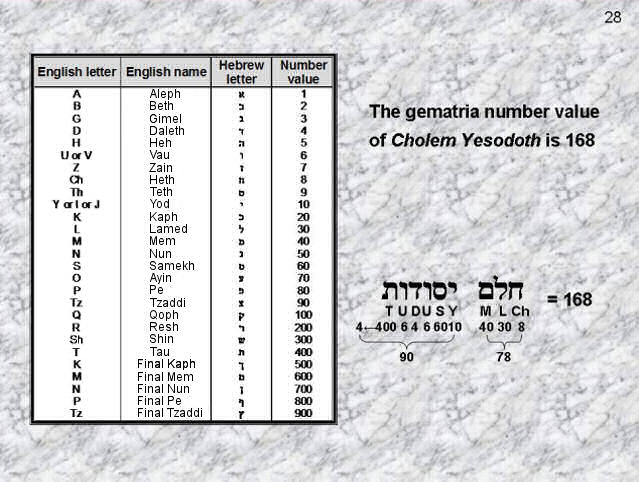
Figure 29
The
disdyakis triacontahedron is unique in that
no other Archimedean or Catalan solid has
1680 geometrical elements surrounding an
axis that passes through two opposite
vertices. This is true for polyhedra with
triangular faces whether their faces are
regarded as single triangles (case A) or
whether they are divided into their sectors
(case B). It is also true for polyhedra
having faces that are not
triangular.
|
|
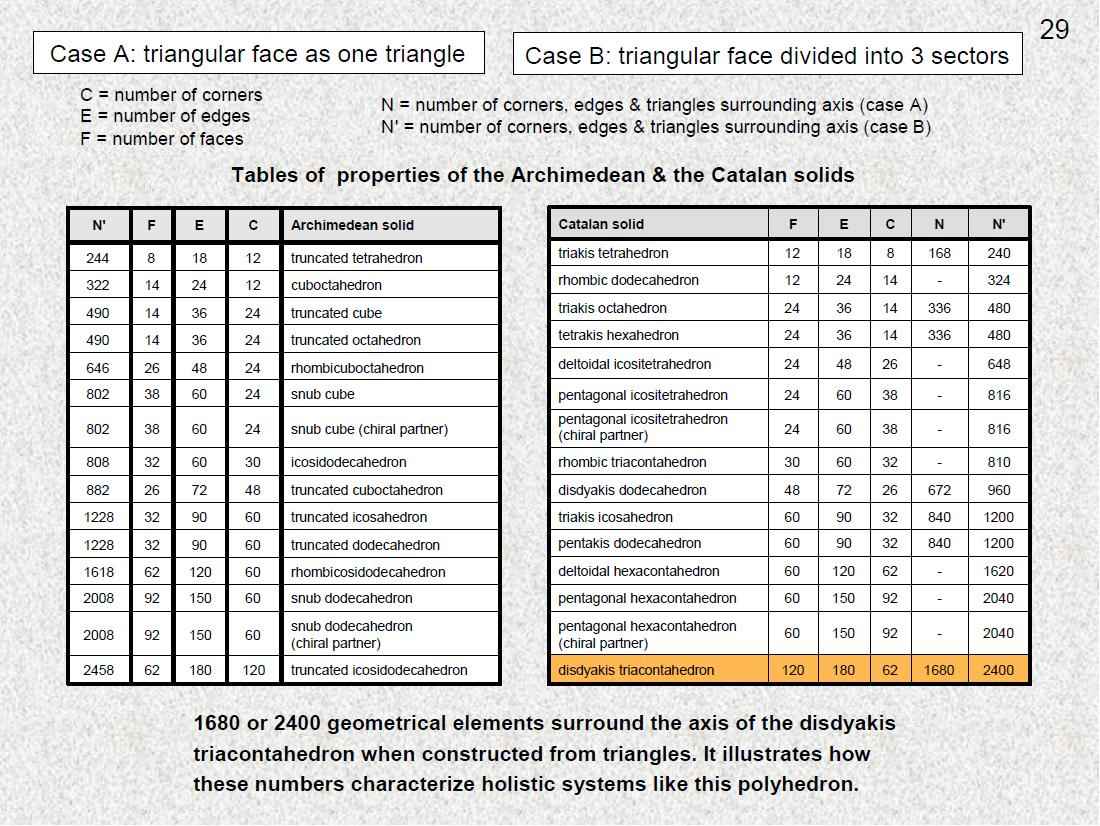
Figure 30
ADONAI,
the Godname of Malkuth (the physical
universe), has number value
65
. It
prescribes the ten lowest Trees of Life in
CTOL because they have 65
SLs.
These Trees map the ten spatial dimensions
predicted by M-theory, the general theory
being currently being sought by physicists
to explain the basic properties of physical
matter and the forces of nature. A decagon
within a square is a representation of the
ten Trees because the object has
65
yods when
the ten sectors of the decagon are
tetractyses. The four corners of the square
correspond to Kether, Chokmah, Binah &
Daath of the tenth Tree and the 61 yods in
the decagon correspond to the 61 SLs up to
Chesed of this Tree. The letter values of
ADONAI are the numbers of different
yods.
|
|
30
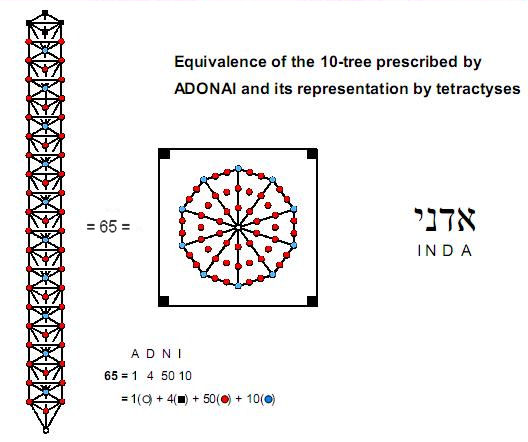
Figure 31
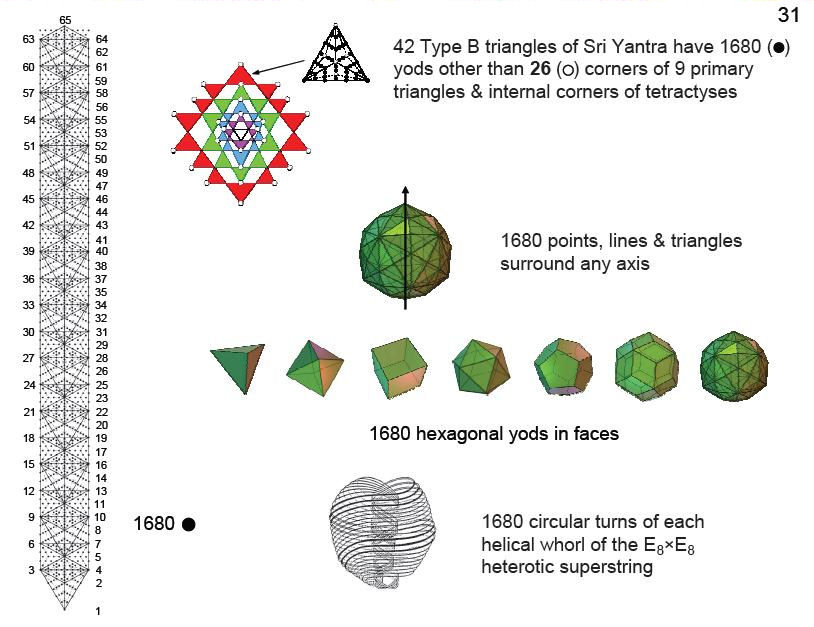
When the triangles in the 10-tree prescribed by
ADONAI are divided into their sectors and each
sector turned into a tetractys, there are 1680
yods below the apex of the tenth Tree of Life
(65th SL),
including those outside it that belong to the
eleventh Tree. Each yod denotes one of the
circular turns in a whorl of the heterotic
superstring described by the Theosophists
Besant & Leadbeater with the aid of a form
of remote-viewing known in yoga as one of the
siddhis, or paranormal abilities. The same
number has been encountered in this article
as:
-
the
1680 yods in the 42 so-called ‘Type B’
triangles of the Sri Yantra other than
internal corners of tetractyses and the
corners of its nine parent
triangles;
-
the
1680 points, lines & triangles
making up the disdyakis triacontahedron
that surround an axis passing through
any two diametrically opposite
vertices;
-
the
1680 hexagonal yods in the faces of the
five Platonic solids, the rhombic
triacontahedron & the disdyakis
triacontahedron;
-
the
1680 hexagonal yods in the faces of
the 21
copies
of the first four Platonic solids whose
vertices belong to the disdyakis
triacontahedron.
The n-tree has (12n+7) triangles with (16n+9)
sides. The number of sides in
their (36n
+
21)
sectors is
16n + 9 + 3(12n+7) = 52n + 30.
The 10-tree has 361 sectors with 550 sides.
This is the counterpart of the 550 geometrical
elements in the
50
faces of the five Platonic solids, the 550
Sephiroth in CTOL and the 550 unshared
geometrical elements in the
15
polygons of the disdyakis triacontahedron. The
tenth Fibonacci number
55
determines the form of all such holistic
systems. In particular, it determines the form
of each of the ten helices that comprise the
E8×E8
heterotic superstring.
|
|
|
Figure 32
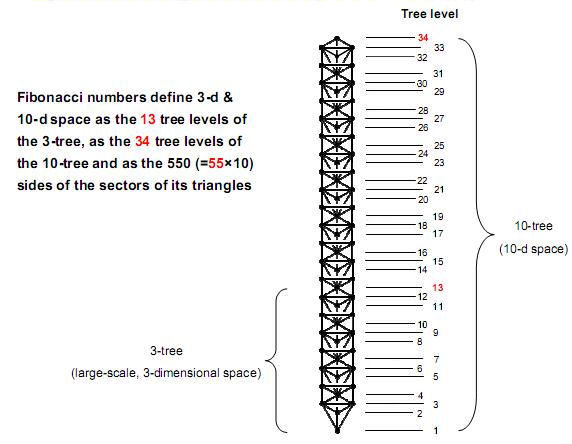
Tree levels are
defined as the formative stages in the Fibonacci
number-governed growth of successive Trees of Life
in CTOL. The number of tree levels in the n-tree
is:
t(n) = 3n +
4.
t(1) =
7, which is the
fourth Lucas number, t(3) = 13, which is the
seventh Fibonacci number and t(10) =
34, which is the
ninth Fibonacci number. This number has appeared in
this article:
1. in the outer
Tree of Life as the number of geometrical elements
in the Upper Face of the 1-tree and as the number of
elements added by successive Trees;
2. in the inner Tree of Life as the
34
corners
associated with each set of seven enfolded
polygons that are intrinsic to them because they
do not coincide with those of polygons enfolded
in the next higher Tree;
3. as the 34
single
bones of the axial skeleton of the human
body;
4. as the 34
vertices
& centres of the first four Platonic
solids;
5. in the disdyakis triacontahedron as the
34
corners
of the 27 sectors of the seven polygons either above or
below the central hexagon that are formed by vertices
of this polyhedron.
Remarkably, it
determines the very number of overlapping Trees of
Life that have a yod population of 1680. In this
way, it
determines the very helical structure of each whorl
of the heterotic
superstring. The sum
34
=
21
+
13
differentiates
between large-scale, 3-dimensional space, which is
mapped by the 3-tree with 13
tree
levels, and the next 21
tree
levels that span seven Trees up to the
34th, which marks the
top of the 10-tree mapping the ten spatial
dimensions. In other words, the eighth Fibonacci
number 21
measures the
seven compactified dimensions predicted by M-theory.
The tenth Fibonacci number 55
determines the
10-tree (and therefore the superstring structural
parameter 1680) because their 127 triangles have 361
sectors with 550 (=55
×10)
sides.
|
|
32
|
References
-
Phillips, Stephen M. Article
27: “How the disdyakis triacontahedron
embodies the structural parameter 1680 of
the E8×E8 heterotic
superstring,” (WEB, PDF).
- Besant, A. & Leadbeater, C.W. “Occult
Chemistry,” 3rd ed., Theosophical Publishing House,
Adyar, Madras, India, 1951.
-
Phillips, Stephen M. Article
36: “The Sri Yantra-like pattern of the 15
layers of vertices in the disdyakis
triacontahedron and its scientific meaning,”
(WEB, PDF).
-
Phillips, Stephen M. Article
49: “How some sacred geometries are
equivalent maps of all levels of reality,”
(WEB, PDF).
-
Phillips, Stephen M. Article
35: “The Tree of Life nature of the Sri
Yantra and some of its scientific meanings,”
(WEB, PDF).
|
|
|