ARTICLE 35
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
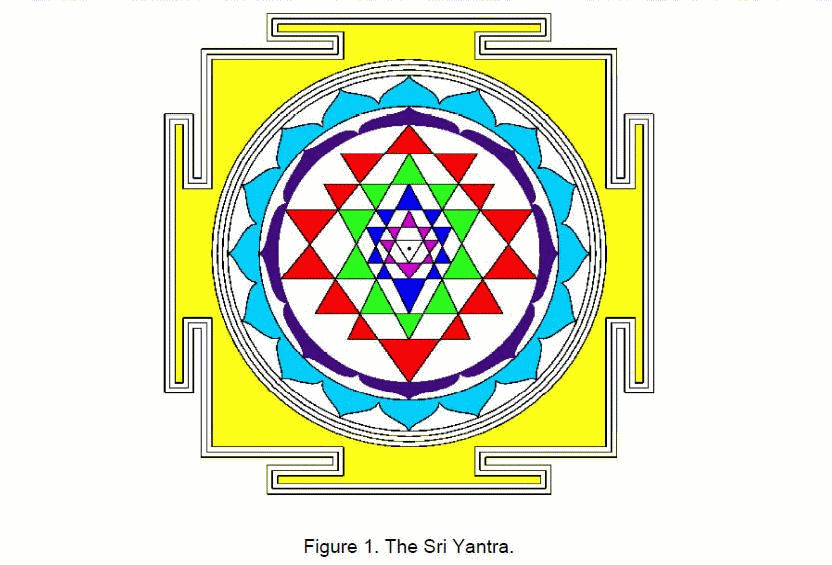
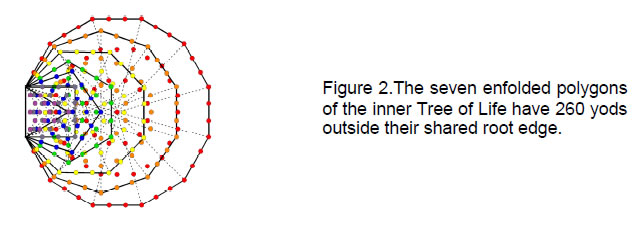
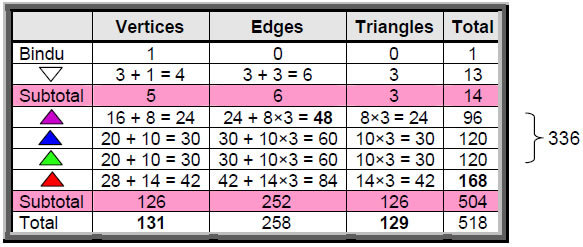
Revered by Hindus as the most sacred of the yantras, the Sri Yantra is said to represent the process of unfolding of Divine Creation. This article confirms their belief by correlating the Sri Yantra with the Tree of Life. The first three layers of triangles have 168 geometrical elements comprising 84 edges and 84 vertices & triangles. As discussed in many previous articles, this number is the structural parameter of the E8×E8 heterotic superstring. The numbers of different types of edges and vertices in these layers are exactly the same as the numbers of various types of non-zero roots making up the 168 non-zero roots of the superstring gauge symmetry group E8 that do not belong to its subgroup E6.The 48 geometrical elements in the first layer of triangles consist of eight groups of six geometrical elements. This 8×6 pattern has parallels in many other holistic systems discussed in previous articles. The Sri Yantra has 260 geometrical elements, showing how it is prescribed by the Godname YAHWEH, whose gematria number value is 26. There are 260 geometrical elements in the seven overlapping Trees of Life that map the seven planes of consciousness. The Sri Yantra is also equivalent to the inner form of the Tree of Life, which has 260 yods outside its root edge when the sectors of its seven polygons are tetractyses. When each is divided into three triangles, the 14 triangles of the fourth layer have 168 geometrical elements and the 28 triangles of the first three layers have 336 elements. These numbers are the numbers of circularly polarised oscillations in, respectively, a half-revolution and a whole revolution of each curve making up the E8×E8 heterotic superstring. They correspond to the 168 automorphisms of the Klein Quartic and to its 336 automorphisms and anti-automorphisms. There are also 336 yods on the edges of the 42 triangles in the four layers. The 70 vertices of the 2-d Sri Yantra correspond to the 70 yods of the outer Tree of Life constructed from tetractyses. The 236 geometrical elements making up the four layers correspond to the 236 yods on the boundaries of the 14 polygons in the inner Tree of Life. The 2-d Sri Yantra is equivalent to the disdyakis triacontahedron with 362 geometrical elements in its faces because its four layers of triangles have 362 yods. The 8:6 division of tips of triangles in the fourth layer reflects the eight Pythagorean and six non-Pythagorean notes in the seven musical scales. The numbers in Plato’s Lambda appear within in the Sri Yantra in its nine basic triangles regarded as tetractyses. The seven positive and seven negative points of these Shiva and Shakti triangles symbolize the seven Yang and the seven Yin acupuncture meridians. They also signify the seven notes and their complements that make up the seven musical scales. |
1
1. Sri Yantra
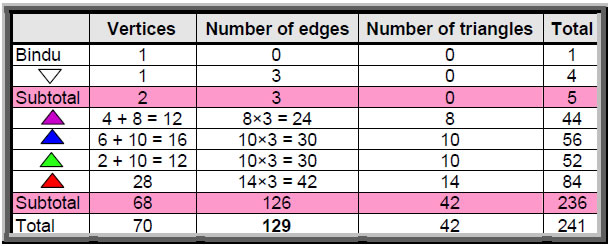
The Sri Yantra (Fig. 1) is revered by Hindus as the most powerful and sacred of the yantras, or images used for meditation. Five downward pointing triangles that symbolize the feminine creative energy, or Shakti, intersect four upward-pointing triangles symbolizing the masculine creative energy, or Shiva. This generates 42 triangles arranged in
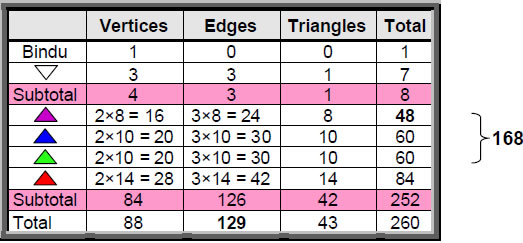
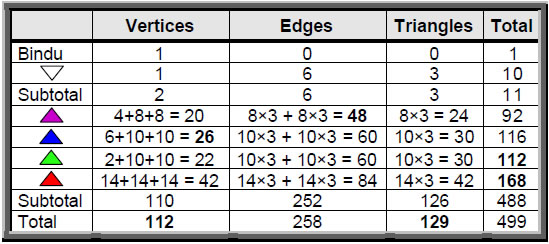
four layers of eight, 10, 10 and 14 triangles. They surround a downward pointing triangle whose corners denote the triple Godhead of Shiva, Brahma and Vishnu. At its centre is a point, or bindu, representing the Absolute. Table 1 shows the numbers of vertices, edges and triangles in the Sri Yantra.
Table 1. Geometrical composition of the Sri Yantra.
2
Table 2. Gematria number values of the ten Sephiroth in the four Worlds.
ANGELS
CHAKRA1 Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the Presence)
314Chaioth ha Qadesh
(Holy Living Creatures)
833
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
6362 Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of
the Zodiac)
1403 Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation of God)
311
Aralim
(Thrones)
282
Shabathai
Rest.
(Saturn)
317Daath
(Knowledge)
4744 Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence of God)
62Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness.
(Jupiter)
1945 Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement Strength.
(Mars)
956 Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light.
(Sun)
6407 Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97Tarshishim or
Elohim
1260
Nogah
Glittering Splendour.
(Venus)
648 Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light.
(Mercury)
489 Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living God)
49, 363Gabriel
(Strong Man of God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame.
(Moon)
8710 Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and King)
65, 155Sandalphon
(Manifest Messiah)
280Ashim
(Souls of Fire)
351
Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168
3
The 42 triangles in the four levels have 84 vertices and 126 edges. The Godname EHYEH (see Table 2) prescribes the number of triangles because 42 is the 21st even integer. It prescribes the number of edges because 126 is the sum of the values of all the possible combinations of the three letters A, H & I in AHIH:
1 A + H + I = 16 2 AH + HI + AI + HH = 42 3 AHI + HIH + AHH = 47 4 AHIH = 21 = 126 The number of vertices is 84, where
84 = 12 + 32 + 52 + 72.
The number of geometrical elements is 252, which is the 126th even integer.
The first three levels have 84 edges, 56 vertices and 28 triangles, that is, 84 vertices and triangles, totalling 168 geometrical elements. This equal 84:84 division of the number value 168 of Cholem Yesodoth, Mundane Chakra of Malkuth, has been encountered in many previous articles. Examples are:
1. Article 15,1 which discussed the 84 permutations of pairs and triplets of octonions belonging to the seven 3-tuples of octonions (ei, ei+1, ei+3) and the 84 permutations of their inverses;
2. Article 18,2 which discussed the I Ching table of 64 hexagrams and the 28 hexagrams on either side of its diagonal. Each hexagram is a pair of trigrams, so that each set of 28 off-diagonal hexagrams has (28×2×3=168) lines and broken lines. Each set comprises 84 lines and 84 broken lines;
3. Article 21,3 which discussed the 84 hyperbolic triangles in each of the two types of seven similar slices of the Klein Configuration, the diagram whose 168 hyperbolic triangles represent the 168 automorphisms of the equation known to mathematicians as the Klein Quartic;
4. Article 16,4 which discussed, firstly, the 84 repetitions of the Pythagorean-valued, rising intervals between the notes of the seven types of musical scales and their 84 falling intervals (pp. 17–18), and, secondly, the 84 yods belonging to the first four enfolded polygons enfolded in each half of the inner Tree of Life that either are not centres of polygons or do not coincide with Sephiroth (pp. 23–24).
5. Article 33,5 which found that the lowest five of the seven polygons formed by vertices of the disdyakis triacontahedron have 84 vertices & triangles and 84 edges.
The 84:84 division is an indication that the Sri Yantra constitutes sacred geometry that is isomorphic to other systems of sacred geometry. This conclusion is spectacularly
4
confirmed by the fact that, together with the eight geometrical elements in the central triangle and bindu, the Sri Yantra has 260 geometrical elements. This is the number of yods outside the root edge of the seven enfolded polygons making up the inner form of the Tree of Life when their 47 sectors are turned into tetractyses (Fig. 2). The Godname YAHWEH with number value 26, which expresses the creative power of God, prescribes how many geometrical elements the Sri Yantra comprises.
The 168 elements of the first three layers comprise 56 vertices, 84 edges and 28 triangles. The 56 vertices consist of 28 that form the bases of the triangles and 28 that are their apices. The 84 edges consist of 28 that are bases of outward pointing triangles and 28 pairs of edges forming their points. Hence, the composition of the 168 elements is:
56 vertices = 28 base vertices + 28 apices
28 base edges
28 edges
28 edges
28 trianglesCompare this with the forms of the 8-tuples and their numbers representing the 168 nonzero roots of the superstring gauge symmetry group E8 that are not also non-zero roots of its exceptional subgroup E6:
We find that the numbers of types of geometrical elements making up the first three layers of the Sri Yantra are the same as the numbers of different 8-tuples of non-zero roots belonging to E8 but not to E6. The geometry of the 28 triangles in these three layers is analogous to the permutations of 8-tuples representing these non-zero roots!
The 43 triangles have 129 edges, where 129 is the number value of YAHWEH SABAOTH, Godname of Netzach. The innermost triangle consists of two edges that meet at the middle of an edge of the lowest triangle of the fourth layer and one edge that joins
5
vertices of triangles in that layer, which is composed of 24 edges. The 27 edges of the central triangle and first layer therefore divide into (26+1) edges. This means that the 129 edges consist of 26 edges of the central triangle and first layer and 103 edges of the central triangle and other three layers. 26 is the number value of YAHWEH and 103 is the number value of SABAOTH.
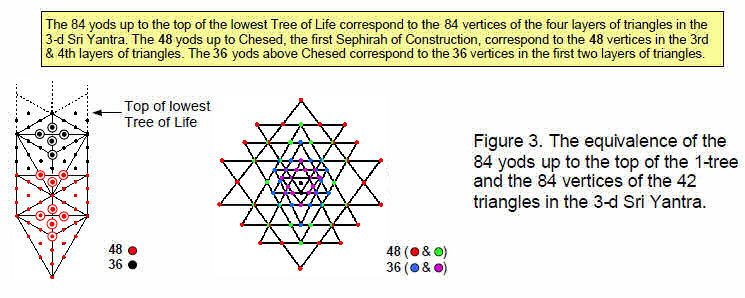
The first layer has 48 geometrical elements consisting of eight pairs of vertices, eight triplets of edges and eight triangles, that is, eight groups of six elements. 48 is the number value of Kokab, the Mundane Chakra of Hod. The third
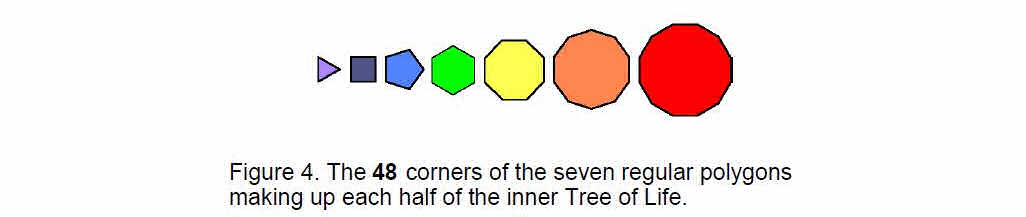
& fourth layers of triangles have 48 vertices and the first & second layers have 36 vertices (Fig. 3). They correspond to the 48 yods up to Chesed of the 1-tree and the 36 yods above it. The seven separate polygons in the inner Tree of Life have 48 corners and seven centres (Fig. 4). These correspond to the 48 elements of the first layer of triangles and to the seven elements of the central triangles.
The bindu point at the centre of the Sri Yantra is surrounded by 87 vertices of 43 triangles with 129 edges, that is, by (87+129=216) vertices and edges. 216 is the number value of Geburah and 87 is the edges and 126 vertices and
triangles in the four layers of triangles surround number value of Levanah, the Mundane Chakra of Yesod. 126 the bindu. Including the innermost triangle, the 260 geometrical elements are made up of 126 edges of the four layers of triangles and 134 geometrical elements made up of 88 vertices, three edges and 43 triangles. This 126:134 division is reflected in the 260 yods outside the root edge of the seven enfolded polygons as the 126 yods in the decagon and dodecagon and as the 134 yods in the first five polygons (Fig. 5). It is further confirmation of the Tree of Life nature of the Sri Yantra. Corresponding to its 88 vertices and 129 edges are the 88 edges of the 47 sectors of the seven enfolded polygons in the inner Tree of Life and their 129 vertices and edges.
2. Sri Yantra with triangles divided into sectors
Suppose that each triangle in the Sri Yantra is divided into its sectors. Table 3 below displays the numbers of resulting vertices, edges & triangles.6
Table 3. Geometrical composition of the 3-d Sri Yantra.
There are 131 vertices, where 131 is the number value of Samael, the Archangel of Geburah. This property is prescribed by the Godname ADONAI with number 65 because 131 is the 65th odd integer after 1. Below the bindu are 130 vertices. Whereas there are 126 edges in the four layers of triangles when the latter are single tetractyses, there are 126 vertices when the triangles are constructed from three tetractyses. There are also 126 triangles. The Godname YAHWEH SABAOTH with number value 129 prescribes the 129 triangles and the 130 vertices because 130 is the 129th integer after 1.
According to Table 3, the fourth layer of triangles has 168 geometrical elements made up of 84 edges and 84 vertices and triangles. Compare this with its 84 elements when the triangles are single tetractyses and with the 168 elements of
the first three layers. What was in the latter now appears in the fourth when the triangles are divided into three. The first three layers have 336 elements made up of 168 edges and 168 vertices and triangles. This 168:168 division appears in
7
the Klein Configuration as the 168 hyperbolic triangles representing the 168 automorphisms of the Klein Quartic and the 168 triangles representing its 168 anti-automorphisms.6 As discussed in many previous articles, it appears in the E8×E8
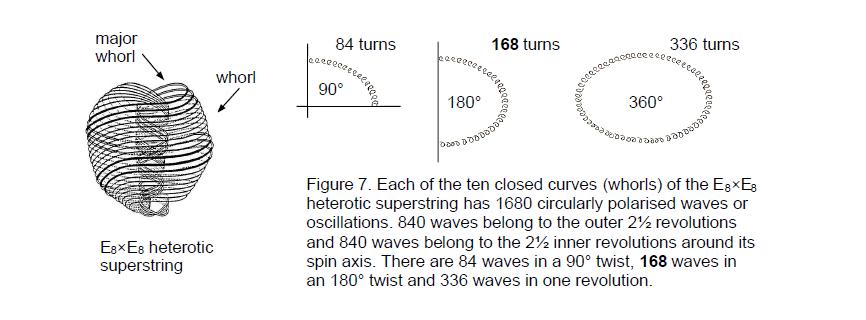
heterotic superstring as the 168 circularly polarised oscillations made in half a revolution of each of its ten curves, the 168:168 division reflecting the distinction between the outer and the inner halves of each curve (Fig. 7). It appears in the disdyakis triacontahedron as the 168 geometrical elements in its faces above the central layer of vertices and their 168 mirror-image elements in its faces below it.7
The four layers of triangles have 504 geometrical elements made up of 168 elements in the fourth layer and 336 elements in the first three layers (168 edges and 168 vertices and triangles). This 168:168:168 composition manifests (apart from the Tree of Life factor of 10) in the heterotic superstring as the 1680 oscillations in each of the three major whorls (the thicker whorls shown in Fig. 7). The geometry of the Sri Yantra encodes that
Table 4. Geometrical composition of the 2-d Sri Yantra.
8
part of the superstring that is the counterpart of the Supernal Triad of Kether, Chokmah and Binah, or Shiva, Brahma and Vishnu. The counterpart of the 504 geometrical elements in its four layers of triangles is the 504 oscillations in half a revolution of its three major whorls.
If the triangles are divided into three triangles and then each of the latter is three triangles, it is found that the four layers of triangles have 252 vertices, 630 edges and 378 triangles, totalling 1260 geometrical elements. This is the number value of Tarshishim, the Order of Angels assigned to Netzach.
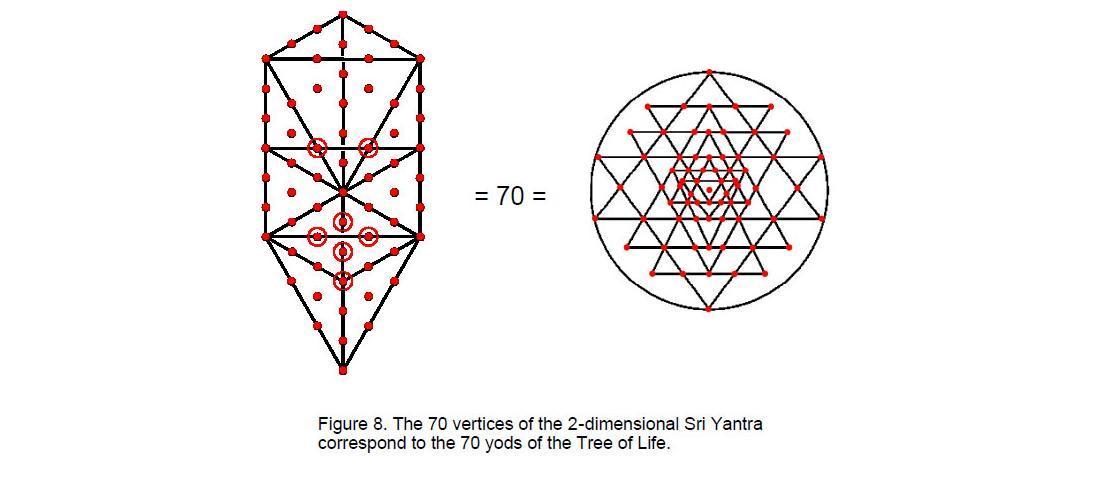
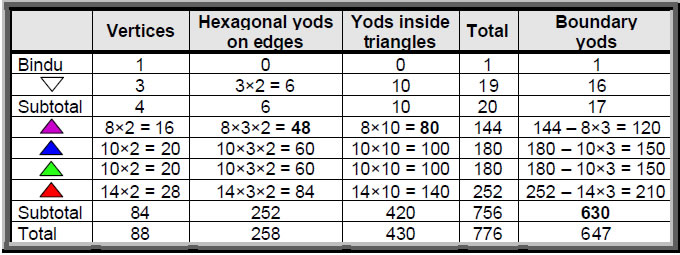
If the 3-dimensional Sri Yantra is projected onto a sheet, the numbers of edges and triangles are unchanged but the number of vertices is reduced (Table 4). As before, the fourth layer has 28 vertices. The third layer has 12 vertices instead of 20 vertices, the second layer has 16 vertices instead of 20 vertices and the first layer has 12 vertices instead of 16. The projection of the four layers now comprises 68 vertices instead of 84, that is, 16 fewer vertices. The innermost triangle adds one vertex. Including the bindu, the projected Sri Yantra therefore has
(1+1+68=70) vertices. This is the number of yods in the Tree of Life when its 16 triangles are turned into tetractyses (Fig. 8). It is also the number of corners of the two sets of seven enfolded polygons. The two ends of the root edge correspond to the bindu and the lowest vertex of the central triangle. In each case, the two points do not shape the holistic structure because they represent its seed source, in the latter case the bindu being an isolated point and the lowest vertex being not at a corner of a triangle but at the midpoint of the edge of one. The 68 vertices of the four layers of triangles correspond to the 68 corners of the 14 polygons outside their shared root edge.
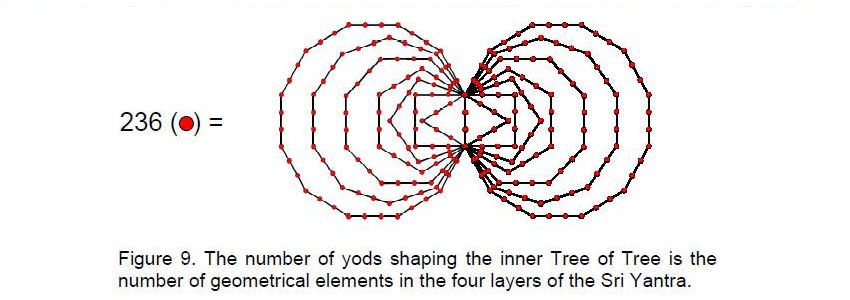
Instead of having 252 geometrical elements (see Table 1), the four layers of triangles now have 16 fewer, i.e., 236 elements. This is the number of yods on the boundaries of both sets of seven enfolded polygons (Fig. 9). As in the 3-dimensional case, the four layers of triangles in the 2-dimensional Sri Yantra have 126 edges of 42 triangles. Now, however, it has (68+126+42=236) geometrical elements. The central triangle adds one vertex and three edges but not a triangular area because it has a point at its centre. Including this bindu, the 2-dimensional Sri Yantra has (236+1+3+1=241) geometrical elements. In other words, 240 geometrical elements surround the bindu. 168 of these are either edges or triangles (see Table 1) and the remaining 72 elements consist of the 68 vertices of the 42 triangles, the single vertex of the central triangle unshared with other triangles, its three edges and the bindu. This property is remarkable because the division: 240 = 72 + 168 corresponds in the superstring gauge symmetry group E8 to the 72
9
non-zero roots of E6 and the remaining 168 non-zero roots of E8. The geometrical composition of the 2-dimensional Sri Yantra therefore reflects the root composition of E8 and its subgroup E6.
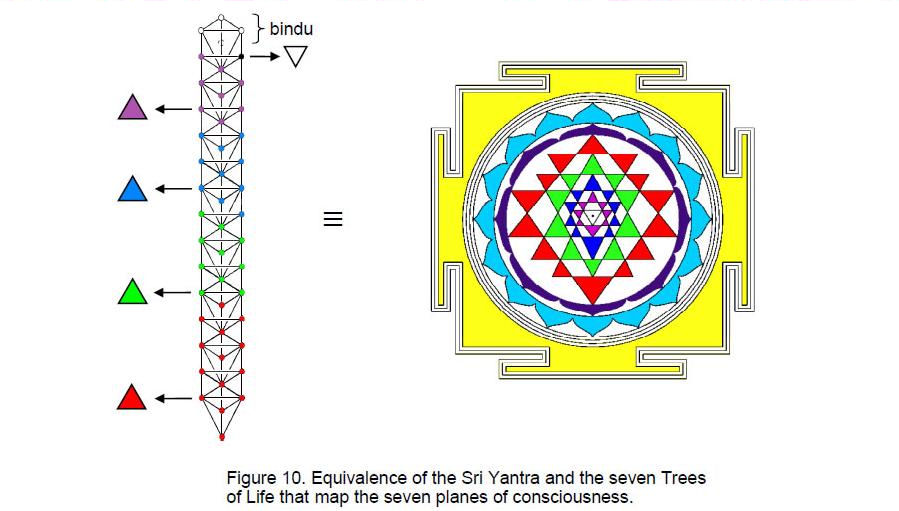
Seven overlapping Trees of Life have 47 Sephirothic emanations (called “Sephirothic levels,” or SLs). There are 43 SLs up to Chesed of the seventh tree, the formative, starting point of the emanation of the seven Sephiroth of Construction, each mapped by a tree. This is the number of triangles in the Sri Yantra (Fig. 10). Each triangle symbolizes one of the seven-fold differentiations of the seven Sephiroth of Construction. Each tree maps one of the seven planes of
consciousness: in Theosophical terms, the physical, astral, mental, buddhic, atmic, anupadaka and adi plane. As all the spiritual realms as varieties of consciousness symbolized by triangles emerge from the Absolute symbolized by the bindu, so successive SLs emanate from the Supernal Triad of the highest tree. The central triangle symbolizes the commencement of ‘objective’ existence — not in a physical sense but in the metaphysical sense of separation from the subjective unity of God symbolized by the bindu point of the Sri Yantra and by the Supernal Triad at the top of the first Tree of Life.
Spectacular confirmation that the Sri Yantra is equivalent to seven overlapping Trees of Life comes from considering the geometrical composition of a set of n overlapping Trees:
Number of vertices of triangles ≡ S(n) = 6n + 4.
Number of edges of triangles ≡ E(n) = 16n + 6.
Number of triangles ≡ T(n) = 12n + 4.
Number of tetrahedra ≡ t(n) = n + 1.Number of geometrical elements in n Trees of Life = S(n) + E(n) + T(n) + t(n) = 35n + 15. Hence, seven Trees of Life have 260 geometrical elements made up of 46 vertices (S(7)), 118 edges (E(7)), 88 triangles (T(7)) and eight tetrahedra (t(7)). Compare this with the
10
composition of the Sri Yantra indicated in Table 1: 260 geometrical elements comprising 88 vertices, 129 edges and 43 triangles. Amazingly, both the Sri Yantra and seven Trees of Life have the same number of geometrical elements! The latter has 252 vertices, edges and triangles — the same number that the four layers of triangles have. The eight elements possessed by the bindu and innermost triangle correspond to the eight tetrahedra in the seven Trees of Life. The number 88 applies to vertices in the Sri Yantra and to triangles in the seven Trees of Life. What is so significant here is not only that both structures have the same number of geometrical elements but also that this number is 260 — the number of yods in 26 tetractyses and the number of yods needed to construct the inner form of the Tree of Life, starting from the root edge (see Fig. 5). This is additional evidence that the Sri Yantra represents the seven Trees of Life mapping the seven planes of consciousness.
In my book “The Mathematical Connection between Religion and Science,”8 I showed how, when considered separately, the seven polygons making up the inner Tree of Life have, when constructed from tetractyses, as many yods as there are SLs up to the first Sephirah of Construction of the 49th Tree. In other words, the seven enfolded polygons encode seven overlapping Trees and the seven separate polygons encode 49 overlapping Trees. Each plane of consciousness mapped by a Tree of Life has seven subplanes that, too, can be mapped by a Tree of Life, making (7×7=49) Trees. The Sri Yantra is a map of the seven planes of consciousness that can be mapped both by seven Trees and by 49 Trees. The latter is simply the seven-fold differentiation of the former.
3. Yod composition of the Sri Yantra
Suppose that each of the 43 triangles in the Sri Yantra is turned into a tetractys. Table 5 shows the numbers of yods in each layer.Table 5. Yod population of the 3-d Sri Yantra (triangles as tetractyses).
The four layers of triangles have 378 yods, of which (378–42=336) yods lie along their 126 edges. The latter yods are made up of 84 vertices, 84 hexagonal yods on the 42 edges of the fourth layer and 168 hexagonal yods on the 84 edges of the first three layers. Once again, we encounter the superstring structural parameters 84, 168 and 336. The number 336 is the number of yods needed to form the boundaries of all 42 triangles in the four layers. It has the same 168:168 division as found earlier for the geometrical elements composing the first three layers of triangles. The number 336 defines the shapes of the triangles in the four layers, confirming its shape-defining character vis-à-vis the heterotic superstring as the number of times each of its ten curves oscillates during one complete revolution as it spirals around its spin axis. This result is very satisfying, for it not only confirms the validity of Besant’s and Leadbeater’s account of superstrings over a century ago but confirms the nature of the Sri Yantra as the blueprint for matter.
11
The number of yods on the edges of the 14 triangles is 112. This is the number value of Beni Elohim (“Sons of God”), the Order of Angels assigned to Hod. The first layer of triangles has 64 such yods, 48 being hexagonal ones. 48 is the number value of Kokab, the Mundane Chakra of Hod. 64 is the number value of Nogah, the Mundane Chakra of Netzach, the Sephirah preceding Hod in the Tree of Life. There are 87 corners of the 43 triangles. 87 is the number value of Levanah, Mundane Chakra of Yesod. 168 — the number of edges and triangles in the four layers — is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. This demonstrates how the number values of the Mundane Chakras of the last four Sephiroth define properties of the Sri Yantra.
Now consider each triangle constructed from three tetractyses. Table 6 displays the number of yods in each layer.
Table 6. Yod population of the 3-d Sri Yantra (triangles as three tetractyses).
There are 776 yods, of which 88 yods are vertices of the Sri Yantra before it is constructed from tetractyses. (776–88=688) extra yods are needed to build it. The fourth layer of 14 triangles has 210 yods on their boundaries, showing how the Godname EHYEH with number value 21 prescribes the last layer. Suppose, however, that we regard the central triangle as not transformable into a tetractys or three tetractyses because it signifies the triple Godhead. As before, there are 88 vertices, but now there are 252 hexagonal yods on the edges and 420 yods inside triangles, totalling 760 yods. The Godname YAHWEH ELOHIM (“God the Creator”) with number value 76 prescribes the number of yods needed to construct the Sri Yantra because it can be built from the yods in 76 tetractyses — further evidence that it represents the creative design of God.
12
The number of vertices of the 126 tetractyses in the four layers of 42 triangles = 84 + 42 = 126. The bindu and central triangle (undivided into tetractyses) have four vertices, so that the Sri Yantra has 130 vertices. This is the 65th even integer, showing how ADONAI with number value 65 prescribes the form of the Sri Yantra. It illustrates the shape-defining nature of this Godname of Malkuth, the Sephirah signifying the ‘body’ of Adam Kadmon, or the outer form of the Tree of Life.
The 42 triangles in the four layers have 756 yods, that is, (756–84=672) yods other than their 84 vertices. Their 126 tetractyses have 126 vertices and (756–126=630) hexagonal yods. As each triangle has nine hexagonal inside it, there are (9×42=378) hexagonal yods inside the triangles and 252 hexagonal yods on their edges. Table 5 indicates that the first three layers of 28 triangles have 168 hexagonal yods on their 84 edges and 280 yods inside them. 280 is the
number value of Sandalphon, the Archangel of Malkuth, whose Mundane Chakra has the number value 168. This conjunction of two numbers belonging to the same Sephirah illustrates how Godnames, Archangelic Names, etc collectively define an object like the Sri Yantra that embodies the divine archetypes.
Let us next consider the projection of the Sri Yantra onto a sheet. Firstly, we will analyse the case where the triangles are single tetractyses. Table 7 lists the numbers of yods.
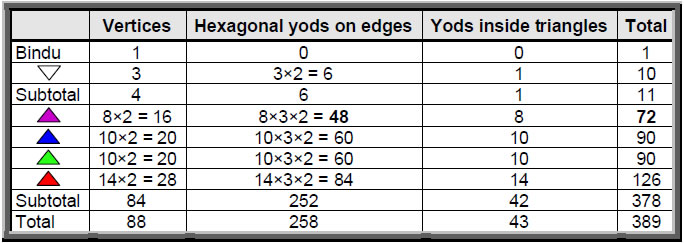
Table 7. Yod population of the 2-d Sri Yantra (triangles as tetractyses).
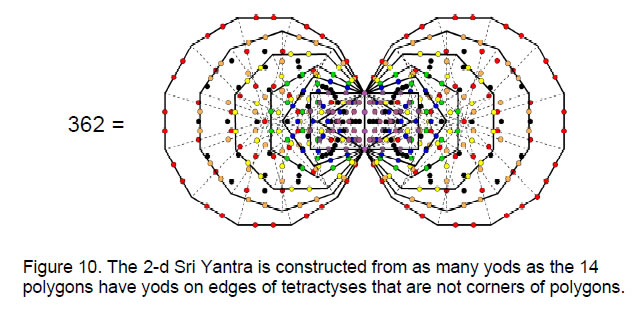
The 84 vertices of the 42 triangles now become 68 vertices, i.e., 16 fewer. The four layers of triangles now have 362 yods instead of 378 yods. This is the number of yods other
13
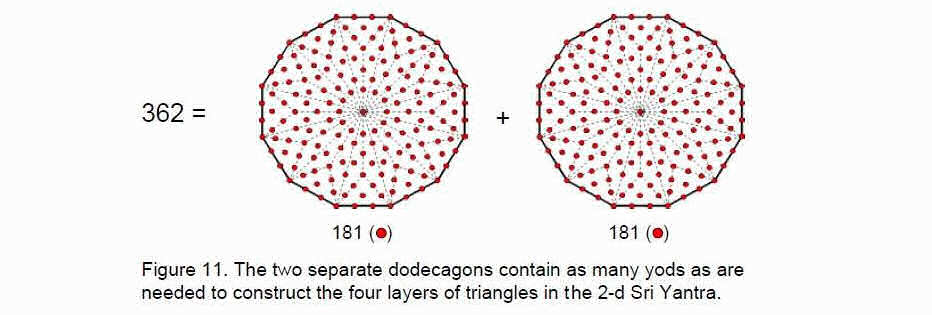
than corners of polygons needed to create the edges of the 94 tetractyses in both sets of seven polygons in the inner Tree of Life (Fig. 10). 362 is also the number of yods in the two dodecagons when their 24 sectors are divided into three
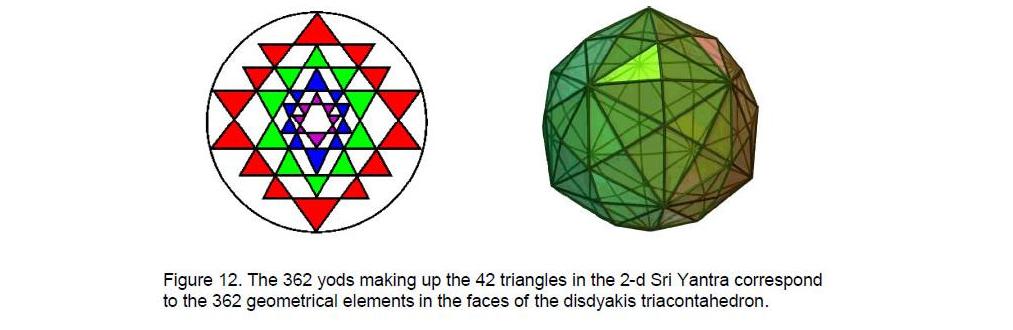
tetractyses (Fig. 11). Most significant of all, it is the number of geometrical elements making up the faces of the disdyakis triacontahedron, which has 62 vertices, 180 edges and 120 triangular faces. This connects the Sri Yantra with this polyhedron, for both are parameterized by the
14
same number of bits of information — yods or geometrical elements.
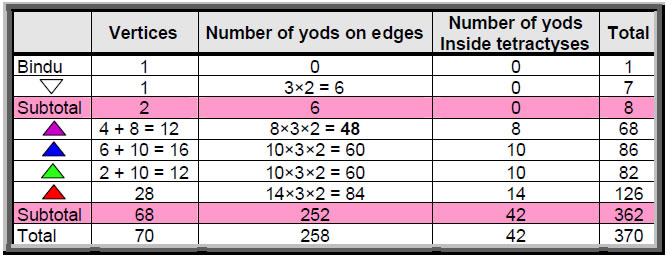
Consider next the 2-d Sri Yantra with their triangles constructed from three tetractyses. Table 7 indicates that, Instead of 756 yods (see Table 6), the 42 triangles now regarded as in one layer have 740 yods. Instead of 630 boundary yods, they have 614 yods. The number of yods other than the 68 vertices of triangles is 672. If the central triangle is
Table 8. Yod composition of the 2-d Sri Yantra (triangles as three tetractyses).
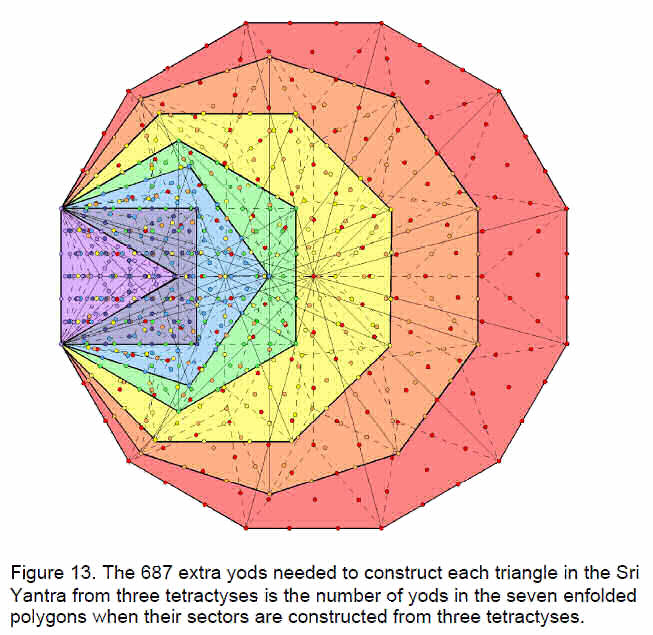
divided into three tetractyses, it has 15 yods other than vertices. The 2-dimensional Sri Yantra therefore has (672+15=687) yods other than vertices. 687 extra yods are needed to construct each of its 43 triangles from three tetractyses. Amazingly, the seven enfolded polygons of the inner Tree of Life have 687 yods! (Fig. 13).
Constructed from three tetractyses, the 42 triangles surrounding the central one have 740 yods that comprise 110 vertices (68 vertices of triangles) and 630 hexagonal yods. The total number of vertices is 112. This is the number value of Beni Elohim, the Order of Angels assigned to Hod. The fourth set of triangles has 252 yods (42 vertices & 210 hexagonal yods). 42 hexagonal yods are centres of the 42 tetractyses, leaving (210–42=168) hexagonal yods lining the edges of these tetractyses. The superstring structural parameter 168 defines the shape of the 42 tetractyses in the 14 triangles, showing how superstring structure is embodied in the Sri Yantra.
4. The Sri Yantra defines the seven musical scales
As shown in Article 14,9 the seven types of musical scales have 14 different notes with tone ratios:1 256/243 9/8 32/27 81/64 4/3 1024/729 729/512 3/2 128/81 27/16 16/9 243/128 2
(Numbers in red denote notes not belonging to the Pythagorean scale (C-scale). Including the tonic, they consist of seven pairs that, as intervals, span an octave. In order of increasing pitch, they are:
1 2 3 4 5 6 7 15
The seven notes in the first column consist of four Pythagorean notes and three non-Pythagorean notes; similarly for their complements in the second column. The 14 notes therefore consist of eight Pythagorean notes and six non-Pythagorean notes.
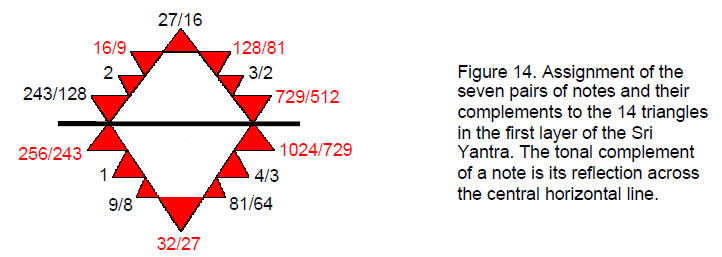
Compare this division of types of notes in the seven musical scales with pattern of triangles in the first layer of the Sri Yantra. Each of the seven triangles in the upper half has its counterpart in the lower half (not every pair, however, is, literally, a pair of mirror images, for only the four triangles joined across the central, horizontal line are identical).
Six of the 14 triangles touch the circumscribing circle. They can be thought of as corresponding to the six non-Pythagorean notes, whilst the eight triangles whose apices do not touch the circle correspond to the eight Pythagorean notes (Fig. 14). Each note assigned to the point of a triangle has a complement assigned to the point that is its mirror image. The pattern of the fourth layer of triangles differentiates between not only the notes and their complementary partners but also the Pythagorean and non-Pythagorean notes!
5. Connection between the Sri Yantra and Plato’s Lambda
According to Plato, the demiurge measured the World Soul with the harmonic proportions of the Pythagorean musical scale by taking a strip of it and dividing its length into portions measured by the first four numbers of the two geometric series: 1, 2, 4, 8, …and 1, 3, 9, 27, … . However, these seven numbers are but members of a tetractys array of ten numbers (Fig. 16) whose ratios define the tone ratios of the notes of the Pythagorean scale.10 Their sum is 90, the sum of the integers at the corners of the tetractys is 36, the sum of the seven integers arranged at thecentre and corners of a hexagon (shown in Fig. 15 by dashed lines) is 54 and the sum of the integers forming the hexagon is 48. These numbers define the tone ratio 3/2 of the perfect fifth because 54/36 = 3/2 and the tone ratio 4/3 of the perfect fourth because 48/36 = 4/3.
The Sri Yantra is formed by the intersection of nine triangles. Let us regard each triangle as a tetractys. The nine tetractyses have 90 yods, of which 36 are corners or centres and 54 are hexagonal yods surrounding their centres. The 36:54 division of yods corresponds to the two sums of numbers at the corners of the Lambda tetractys and at the centre and
16
corners of the hexagon. The sum of the nine integers surrounding the central one in the Lambda tetractys is 84. According to Table 1, this is the number of vertices of the 42 triangles formed by the intersection of the nine triangles. Moreover, the first and second layers have 36 vertices and the third and fourth layers have 48 vertices. The former is the sum of the numbers at the corners of the Lambda tetractys and the latter is the sum of the numbers arranged in a hexagon. The first two layers therefore are the counterpart of the corners of the Lambda tetractys and the last two layers are the counterpart of the hexagonal array of six integers.
42 of the 84 vertices are the tips of the 42 triangles and the other 42 vertices are points where triangles join. The 42:42 division of vertices has its counterpart in the Lambda tetractys as the sums of the two pairs of diagonal rows of numbers:
1+2+4+8+27 = 42,
3+12+9+18 = 42.
These correspondences demonstrate that the Lambda tetractys is arithmetically equivalent to the Sri Yantra. The reason for this is that the former is an archetypal array of numbers that generate by combination the properties of the Tree of Life.
The 36:54 division was found11 in the disdyakis triacontahedron as the 360 tetractyses needed to construct each of its 120 triangular faces from three tetractyses and the 540 internal tetractyses needed to construct the 180 interior triangles formed by its 180 edges when each is built from three tetractyses.
A tetractys defines the Sri Yantra in another way. The number 84 is the sum of the squares of the first four odd integers:
84 = 12 + 32 + 52 + 72.
As
12 = 1
32 = 1 + 3 + 5
52 = 1 + 3 + 5 + 7 + 9
72 = 1 + 3 + 5 + 7 + 9 + 11 + 13,84 = 4(1) + 3(3+5) + 2(7+9) + 1(11+13) = 4×1 + 3×8 + 2×16 + 1×24
16 16
8 8 8
1 1 1 1 .84 is naturally expressed as a tetractys array of 10 integers. Moreover, the central integer 8 denotes the innermost eight vertices of the first layer of triangles and the nine surrounding integers add up to 76, which is the number of vertices surrounding them. 76 is the number value of YAHWEH ELOHIM, Godname of Tiphareth, the centre of the Tree of Life. The number value 26 of YAHWEH is the sum of the integers at the corners of the tetractys and the number value 50 of ELOHIM is the sum of the six integers arranged in a hexagon. This is a remarkable conjunction of sacred geometry and number. The sum of either diagonal row of integers is 49, which is the number value of EL CHAI, the Godname of Yesod.
17
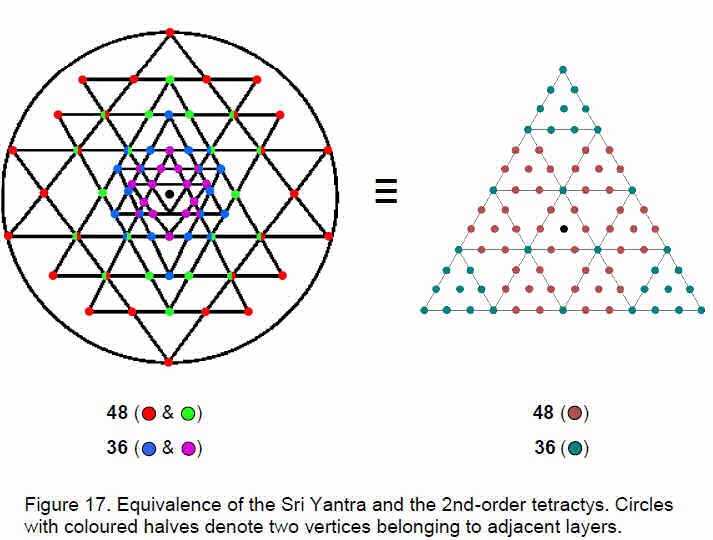
The successive differentiations of divine unity are symbolised by the point, or Pythagorean Monad (0th-order tetractys), the 1st-order tetractys, the 2nd-order tetractys, etc. The next higher order tetractys after Pythagoras’s well-known one is the 2nd-order tetractys (Fig. 16) with 85 yods, where
85 = 40 + 41 + 42 + 43.
84 yods surround its centre. 36 yods lie on its boundary and 49 yods lie inside it, 48 of them surrounding its centre (Fig.17). Compare
this with the fact that the first two layers of
18
triangles in the Sri Yantra have 36 vertices and the last two layers have 48 vertices. The Sri Yantra is equivalent to the 2nd-order tetractys.
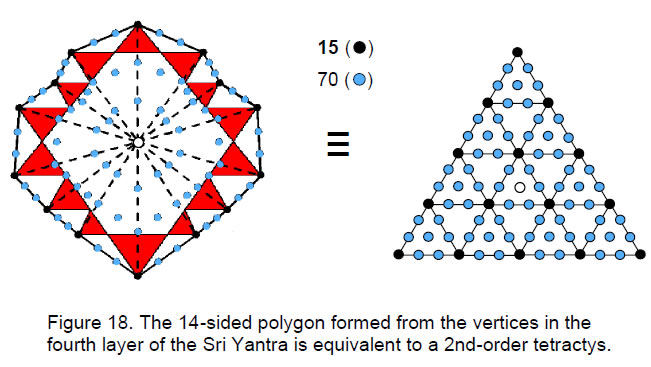
The number of yods in an n-sided polygon whose n sectors are tetractyses is 6n + 1. The tips of the 14 triangles in the fourth layer of the Sri Yantra may be regarded as defining the vertices of a 14-sided polygon (not regular). It contains (6×14 + 1 = 85) yods (Fig. 18). 84 yods surround its centre. The 85 yods comprise 70 hexagonal yods and 15 vertices. This is identical to the pattern of 70 hexagonal yods and 15 vertices in the 2nd-order tetractys. Not only is the whole Sri Yantra equivalent therefore to a 2nd-order tetractys but also the 14-sided polygon marked out by the tips of the 14 triangles in the last layer! Wholeness within wholeness.
The yod populations of the four polygons whose vertices are the tips of triangles are shown below:
Number of hexagonal yods Number of yods 1st layer: 8-sided polygon 2nd layer: 10-sided polygon 3rd layer: 10-sided polygon 4th layer: 14-sided polygon The total number of yods needed to construct the 42 tetractyses in the four polygons is 256 = 44. This is a remarkable illustration of the Tetrad Principle governing holistic patterns.12 The Godname EHYEH with number value 21 prescribes the number of hexagonal yods. The number of yods surrounding the centres of the polygons in the first three layers is 168 and the number surrounding the centre of the 14-sided polygon is 84. It is remarkable that both these superstring structural parameters are embodied in the four polygons. What more convincing evidence that the Sri Yantra encodes the physics of superstrings could one ask for?
When their sectors are divided into three tetractyses, the yod populations of the four polygons are:
Number of hexagonal yods Number of yods 1st layer: 8-sided polygon 2nd layer: 10-sided polygon 3rd layer: 10-sided polygon 4th layer: 14-sided polygon There are 630 yods surrounding the centres of the polygons. 630 is the number value of Seraphim, the Order of Angels assigned to Geburah. In the 2-dimensional Sri Yantra, all the centres coincide, so that 630 yods surround their common centre. The number of yods needed to create the four layers of triangles other than their outermost 14 tips is (634–14=620). This is the number value of Kether (“Crown”).
The four polygons have 546 hexagonal yods. Of these, 126 are centres of 126 tetractyses, leaving 420 hexagonal yods on 210 edges. Including their 88 vertices, there are 508 yods on the edges of the tetractyses. In the 2-dimensional Sri Yantra, 16 vertices of the four polygons merge with other vertices and three centres merge with the fourth, leaving (508–19=489) yods. There are (489–15=474) yods other than the centre and the 14 vertices of the outermost polygon. This is the number value of Daath (“knowledge). It is the number of yods, starting with the bindu, needed to delineate the shapes of the
19
tetractyses composing the 2-dimensional Sri Yantra until the vertices of the last polygon are left.
As Table 9 shows, 474 geometrical elements are needed to construct the four sets of triangles in the 2-d Sri Yantra until its outermost tips are left.
Table 9. Geometrical composition of the 2-d Sri Yantra (triangles as three tetractyses).
The four sets of triangles have 488 geometrical elements, that is, (488–14=474) elements other than the 14 outermost tips of the triangles in the fourth layer. Including the central triangle and the bindu point, the 2-dimensional Sri Yantra has 499 elements. Suppose, however, that the central triangle and bindu are regarded as floating above the planar group of 42 triangles. Instead of adding one vertex according to Table 9, the former would add three vertices because its two other corners no longer coincide with corners of the innermost group of eight triangles, so that 500 (=50×10) elements surround the bindu. This shows in a remarkable way the primary way in which ELOHIM, the Godname of
Binah with number value 50, determines the geometrical composition of the Sri Yantra. The justification for treating the central triangle and bindu as outside the plane of the triangles would be that they symbolize the Absolute and the triple Godhead, which stand outside of Creation represented by the rest of the yantra.
Returning to the discussion of the polygons formed by vertices of triangles, there are 489 yods on edges of tetractyses in the 2-dimensional Sri Yantra, i.e., 488 boundary yods surround the bindu. If the central triangle is constructed from three tetractyses, there
20
are (488+12=500=50×10) boundary yods other than the bindu and the corners of the triangle symbolizing the triple Godhead. This shows how ELOHIM with number value 50 prescribes the population of yods that shape the 2-dimensional Sri Yantra.
6. The Sri Yantra defines the octonions
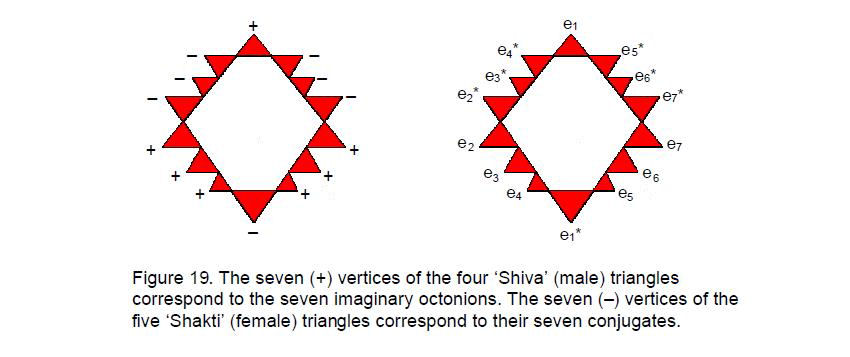
Seven triangles in the fourth layer of the Sri Yantra are tips of three downward pointing triangles said by Hindus to represent the ‘Shakti (female) energy of creation. Seven triangles are tips of upward pointing triangles that represent the ‘Shiva’ (male) procreative energy. Seven tips therefore have a positive polarity and seven have a negative polarity. The seven pairs of positive and negative tips have its counterpart in the fourth (and last) class of numbers known as the octonions, or Cayley numbers. The former correspond to the seven imaginary octonions ei (i = 1–7)and the latter correspond to their conjugates ei* = –ei, where eiei* = 1 (Fig. 19). The seven imaginary octonions form seven 3-tuples (ei, ei+1, ei+3), each having six permutations of pairs and six permutations of all three. This means that the seven 3-tuples have (7×6=42) permutations of pairs and 42 permutations of three octonions.13 This is symbolized in the Sri Yantra as the 42 vertices formed by the convergence or intersection of two edges of the nine triangles and the 42 vertices created by the intersection of three edges, as the following table of numbers of vertices proves:
A vertex formed by the convergence or intersection of two edges symbolizes a permutation of two imaginary octonions and a vertex formed by the intersection of three
21
edges symbolizes a permutation of three octonions. This has significant implications that will not be pursued here.
7. The Sri Yantra defines the 12 acupuncture meridians
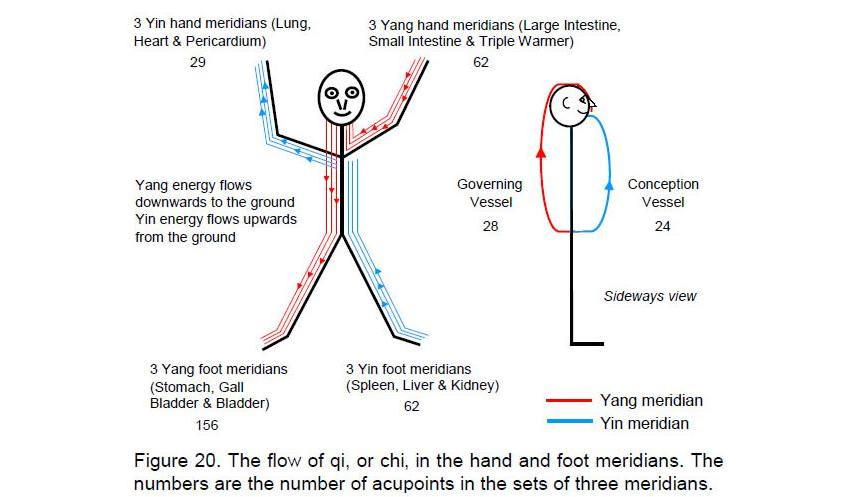
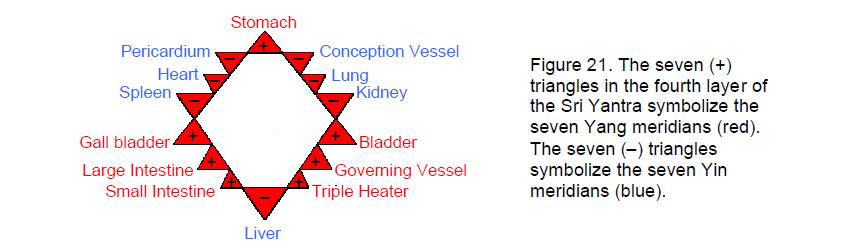
The five downward triangles symbolize the feminine (Shakti) energies of creation and the four upward triangles symbolize the male (Shiva) energies. In Taoist philosophy, they are the Yin and Yang polarities. Another interpretation of the seven positive, or Yang, polarities and seven negative, or Yin, polarities associated with the tips of the triangles in the fourth layer is that the former symbolize the seven Yang meridians and the latter symbolize the seven Yin meridians known in Chinese acupuncture.14 The upper part of the human body has three Yang hand meridians, three Yin hand meridians, the Governing Vessel, which is Yang, and the Conception Vessel, which is Yin (Fig. 20). The lower half of the body has three Yang foot meridians and three Yin foot meridians. The upper and lower halves of the bodytherefore divide the 14 meridians into eight that belong to the former and six that belong to the latter. As with the seven musical scales, the 8:6 division appears in the meridians. The eight triangles of the fourth layer whose tips do not touch the circumscribing circle symbolize the eight meridians in the upper part of the body and the six triangles whose tips touch the circle represent the six foot meridians (Fig. 21). Notice that these triangles are the tips of two intersecting Shiva and Shakti triangles forming a Star of David or Sign of Vishnu. This corresponds to the three Yang foot meridians (Stomach, Gall Bladder and Bladder) and to the three Yin foot meridians (Spleen, Kidney and Liver).
References
1 Phillips, Stephen M. Article 15: “The Mathematical Connection between Superstrings and Their Micro-psi Description: a Pointer Towards M-theory,” (WEB, PDF), p. 13.
2 Phillips, Stephen M. Article 18: “Encoding of Planetary Distances and Superstring Structural Parameters in the I Ching Table,” (WEB, PDF), p. 19.
3 Phillips, Stephen M. Article 21: “Isomorphism Between the I Ching Table, the 3×3×3 Array of Cubes and the Klein Configuration,” (WEB, PDF), pp. 3–4.
4 Phillips, Stephen M. Article 16: “The Tone Intervals of the Seven Octave Species and Their Correspondence with Octonion Algebra and Superstrings,” (WEB, PDF).
5 Phillips, Stephen M. Article 34: “The Seven Layers of ‘A’ Vertices in the Disdyakis Triacontahedron Encode the 206 Bones of the Human Skeleton, the Superstring Symmetry Groups E8 and E8×E8 and the Superstring Structural Parameters 168, 336, 840 & 1680,” (WEB, PDF), p. 12.
22
8 Phillips, Stephen M. “The Mathematical Connection Between Religion and Science.” (Antony Rowe Publishing, England, 2009).
9 Phillips, Stephen M. Article 14: “Why the Greek Musical Modes are Sacred,” (WEB, PDF), p. 8; also ref. 4, p. 12.
10 Phillips, Stephen M. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF).
11 Phillips, Stephen M. Article 26: “How the Seven Musical Scales Relate to the Disdyakis Triacontahedron,” (WEB, PDF), p. 29.
12 Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring and Bosonic String Theories,”(WEB, PDF), p. 5.
14 Phillips, Stephen M. Article 32: “Derivation of the Bone & Classical Acupoint Compositions of the Human Body and Their Relationship to the Seven Musical Scales,” (WEB, PDF).
23