1. Tai Chi

In Chinese Taoism, founded by the great spiritual teacher Lao Tzu, reality or nature — both earthly and cosmic — is called the ‘Tao.’ Originally meaning “the Way,” Tao signifies the noumenal order underlying all phenomena. It is not a static state but a dynamic process — a ceaseless cycle of ebb and flow like the tides, of expansion and contraction like the heart, of outgoing and return like the systolic and diastolic phases of the circulation of blood in the body, of building up and breaking down like the anabolic and catabolic stages of metabolism, where complex molecules are built up or broken down with the release of energy, and of perpetual appearance and disappearance, such as the creation and annihilation of virtual subatomic particles in the vacuum.

All manifestations of Tao are generated by the dynamic interplay of two polar opposite forces or tendencies — yang and yin. Yang is the male, fecundating, creative power, the generative principle associated with Heaven, the ultimate source and cause of all things. Yin is the dark, receptive, female and maternal element represented by the Earth. It is the formative, reproductive principle that transmutes the amorphous, undifferentiated energy of creation into a multiplicity of forms. In the ancient geocentric view of the universe, Heaven was the realm of movement and change, whilst earth below was resting. Therefore, yang came to symbolize movement and yin rest. The Taoist symbol of these opposite (but not opposing) tendencies is the Tai Chi Tu, called the “Diagram of the Supreme Ultimate” (Fig. 1). The bright half represents yang and is regarded as the outgoing, positive aspect of a cycle. The dark half denotes yin and is the returning negative phase of the cycle. The two dots in the diagram express the idea that yin is latent in yang and vice versa; each time each force reaches its extreme, it contains in itself already the seed of its opposite. Yang turns into yin and yin into yang in a perpetual cycle of metamorphosis. For example, the energy of a mechanical system consists of its kinetic energy and its potential energy. If the system is one that is isolated from its environment, the law of conservation of energy requires only that the sum of these two types of energies remains constant over time as each varies. Consider the simple harmonic motion of a swinging pendulum. As it rises, it slows because of the opposing force of gravity acting on the bob and it loses kinetic energy (its yang quality). At the same time, it gains potential energy (its yin quality) as it works against gravity until it comes momentarily to rest at the highest point of its swing when its kinetic energy is zero and its potential energy is a maximum. Then it swings back, increasing its kinetic energy but losing potential energy until it reaches the lowest point again, when it regains all its initial kinetic energy and loses all its potential energy. During its upward and downward motion, potential energy — its yin quality — changes into kinetic energy — its yang quality and vice versa. Neither kind of energy is constant. Only their sum is, and there is continual interchange between them.

Subatomic particles, atoms and even molecules behave as either particles or waves. Their observation forces them to act as either one or the other. This dualistic nature of matter was epitomised by the great Danish physicist Niels Bohr in his Principle of Complementarity. The particle picture and the wave picture are ideas of classical physics. Bohr pointed out that each is only partially correct in the real, quantum world and that which aspect is observed depends upon how the observation is carried

2

out. It is not that only one of the two opposite possibilities always exists for a given subatomic object. Instead, waves transform into particles and particles change into waves depending on the mode of observation. Before being observed, the object is neither wave nor particle (the term ‘wavicle’ has been coined to express this unobservable, noumenal aspect of quantum objects). Called into phenomenal being, so to speak, by being observed, the object is forced by the mode of observation to behave either as a wave or as a particle — it cannot act as both at any given instance. The great mystery still for many physicists is how this choice actually comes about, although Bohr would have dismissed the issue as meaningless for the positivistic reason that it is not an observable transformation.  

The complementarity of opposite modes of existence is the manifestation in the microscopic world of the interchangeable duality of yang and yin. When Bohr visited China in 1937, he was deeply struck by the ancient Chinese notion of the polar opposites of yang and yin. Knighted ten years later, he chose the symbol of tai chi tu as the motif for his coat-of-arms (Fig. 2). Its inscription Contraria sunt complementa (Opposites are complementary) expresses his principle of complementarity between the particle and wave aspects of matter. This became an essential component of the ‘Copenhagen school’ of interpretation of quantum mechanics founded by Bohr. This was the orthodox understanding for many years. However, it has come under attack in recent years.¹  

The Chinese calendar divides the year into 24 equal periods marked by the Sun’s position against the tropical zodiac. Each of the twelve Chinese months comprises two periods marked by the Sun moving

through 30°, so that the length of each period is not a fortnight. The ancient Chinese recorded the beginnings of the four seasons by noting the positions of the shadow cast by a vertical pole in the ground, the shortest shadow occurring on the summer solstice and the longest marking the winter solstice.² They drew six concentric circles around the pole, divided them into 24 segments and marked on the circles the increase in length of shadow, measuring from the outermost circle to  

3

the centre from summer solstice to winter solstice and from the centre of the circle to the boundary from winter solstice to summer solstice (Fig. 3). Subtracting from all measured lengths the minimum length of the shadow at summer solstice, they found that the increase in length of the shadow followed a curve like that dividing the Tai Chi in half. As summer was yang and winter was yin, the origin of their symbolic representation is believed to be this ancient observation of the periodic change of the length of shadows cast by the sun throughout the year.  

2. The I Ching

Pronounced “Ee Jing”, I Ching (易經), the Book of Changes, is about 5,000 years old and, as such, is one of the oldest available sources of spiritual wisdom. The scholar Kung Mgan-Kwoh in the second century B.C.E. described the legend that the first Chinese Emperor, Fu Hsi, was responsible for the original creation of I Ching, although there are different stories concerning where he found his inspiration. The most poetic and inspiring concerns a dragon-like creature that climbed from the water near him as he was meditating one day by the River Ho (the Yellow River). He noticed the lines on the creature’s scales, and decided these were to help him in his quest for knowledge. He set about drawing diagrams representing the patterns on the scales of this creature, believing that the diagrams would be sufficient to encompass all wisdom. This article confirms his belief by showing that it encodes the three-dimensional form of superstrings and the distances of the planets from the Sun.    

I Ching symbols are composed of lines representing yin (female) or yang (male) properties. The original I Ching, as produced by Emperor Fu Hsi, consisted of eight symbols called ‘Kwa’ or ‘trigrams,’ each made up of three lines. A line could be either ‘yin,’ the female power, or gentleness: – –, or ‘yang,’ the male power, or strength: ^__. The eight combinations (2×2×2=8) of yin and yang in the three lines of a trigram are:  

Chien   Heaven	Chên        Thunder	K’an Water	Kên Mountain	Tui Lake	Li    Flame	Sun      Wind	K’un           Earth

In 1143 B.C.E., King Wen, whilst under sentence of death, placed the eight trigrams in pairs to produce the 64 ‘hexagrams’ (six-lined symbols) with which we are now familiar. His son, the Duke of Chou, added a commentary on each line in each hexagram and on the symbolism (known as the ‘Hsiang Chuan,’ or the ‘Image’) of a hexagram). This produced (64×6=384) commentaries that still form an essential part of I Ching.  

Centuries later, Confucius added more commentary, known as the ‘Ten Wings.’ The commentary states that “Change has an absolute limit: This produces two modes: The two modes produce four forms, the four forms produce eight trigrams; the eight trigrams determine fortune and misfortune.”  

Over the centuries, I Ching continued to be recognised, and even given religious significance, before it came to France in the early 19th century. In the early 20th

4

century, a German translation of I Ching was completed and published by Richard Wilhelm, who had lived in China for many years. This translation still forms the basis of many of the published I Ching texts.  

Creation of hexagram

I Ching is used as a method of divination in the following way: keeping firmly in his mind the question whose answer he seeks (one is advised to phrase the question unambiguously and to write it down beforehand on a piece of paper), a person tosses three coins.* The results — head or tail — are noted and the procedure repeated to generate six sets of three outcomes. Each result is interpreted according to the rules listed below:  

1.	three tails		changing yang line called “moving yang”
2.	three heads		changing yin line called “moving yin”
3.	two heads + tail		stable yang line ___
4.	two tails + head		stable yin line – –

Only changing lines are reversed, i.e., the moving yang becomes the stable yang line and the moving yin becomes the stable yin line. The hexagram is built up line by line by successive throws of three coins, starting from the bottom line and working upwards towards the top line. If any toss yields three tails or three heads, a separate hexagram is built up from the changing lines. In both cases, the six lines are then divided into two sets of three — the upper and lower trigrams — and the commentary listed in the I Ching for this so- called ‘resolved’ hexagram is consulted, as well as that for the so-called ‘moving’ hexagram containing one or more changing lines, should these appear.³ There are 2⁶ = 64 possible hexagrams (Fig. 5). As each line may be stable or moving, there are 64² = 2¹² = 4⁶ = 4096 pairings of a resolved and moving hexagram, that is, possible outcomes when the hexagram is generated.  

It is not a purpose of this article to judge the validity (or lack thereof) of the I Ching as a system of divination. Rather, it will show how real information about the natural world is embodied in its pattern of lines, just as the Chinese have always claimed.  

3. The form of the subquark superstring

In his Yoga Sutras, the first systematic exposition of the philosophy and practice of

__________________________
*The original divinations, upon which the Book of Changes was written, were performed exclusively with yarrow stalks. Some scholars believe using coins produces inaccurate results because it changes the probabilities and statistics for individual types of lines. This begs the question whether the type of random process generating hexagrams influences the accuracy of I Ching as a divinatory tool. Many methods are used by I Ching practitioners (e.g., see: http://way.to/iching), showing the lack of agreement between them on this issue.  

5

yoga, Patanjali discussed the various paranormal powers that the yogi can acquire. In Aphorism 3.26 of the Sutras, it is stated that the yogi can develop “knowledge of the small, the hidden or the distant by directing the light of superphysical faculty”:

The Sanskrit name for this siddhi is ‘anima,’ meaning ‘mindfulness.’ The author has given it the modern name of ‘micro-psi.’ The ability to experience mental images of objects too small to be seen by the naked eye that are the same as what would be seen in a microscope was claimed by Annie Besant and Charles W. Leadbeater.⁴ These two early leaders of the Theosophical Society published in 1908 their observations of the atoms of many elements using the yogic micro-psi ability that they claimed to have been trained to develop. According to Besant & Leadbeater, chemical atoms were composed of sometimes thousands of basic particles, which they called ‘ultimate physical atoms,’ or UPAs. They noticed two types of UPAs: a positive variety from which the force binding them together flows outwards and a negative type into which this force is directed (Fig. 6). Each type is composed of ten closed curves that spiral side by side 2½ times  down towards the pointed nadir of the object. They then separate into strands of three and seven, each twisting upwards 2½ times in a narrower spiral around the central axis of the UPA towards its top. These curves (called ‘whorls’) never touch and spiral clockwise as seen from the top in the positive UPA and anticlockwise in the negative UPA. The UPA spins about its axis, pulsates and precesses like a spinning top.  

The author showed⁵ that the UPA is a subquark — an as yet undetected constituent of the up and down quarks making up the protons and neutrons in atomic nuclei. Furthermore, their string-like appearance and their winding in a series of progressively smaller circles are consistent with their being superstrings, which are currently believed by many physicists to be the fundamental units of matter. As mirror images of each other, the positive UPA is a subquark carrying positive magnetic charge and the negative variety carries negative magnetic  charge. Each whorl is a closed helix with 1680 turns (Fig. 7). Leadbeater checked this number carefully 135 times. As a whorl makes five complete revolutions whilst winding around the outer and inner halves of the UPA, there are on average 1680/5 = 336 turns in each revolution. A half-revolution comprises 168 turns and a quarter-revolution consists of 84 turns. These numbers are structural parameters of the subquark superstring.  

The positive and negative UPAs (subquarks carrying positive and negative magnetic charges) are the fundamental manifestation in the subatomic world of the opposite but

 

 

 

6

complementary yang-yin polarities symbolized by the Tai Chi. The (+) UPA is a right-handed form whose whorls spiral clockwise. It manifests the yang property of matter (Fig. 8) because it is the source of outwardly directed, hypercolour SU(3) gauge fields that bind the UPAs in groups of three as quarks. The (–) UPA has a left-handed form whose whorls spiral anticlockwise. It manifests the yin quality because it is the sink into which these fields converge.

A plane wave represents a field whose oscillations take place in some fixed direction (Fig. 9). Two plane waves whose oscillations take place in perpendicular planes with the same amplitude and whose phases differ by 90° add up to form a circularly polarised wave whose amplitude is constant and rotates at a constant rate in a plane perpendicular to the direction of both waves (Fig. 10). The circular turns of the whorl shown in Figure 7 are the circularly polarised vibrations of a standing wave. It makes 1680 oscillations, 336 per revolution. 168 oscillations take place in a half-revolution of each whorl of the UPA and 84 occur in a quarter-revolution. In the (–) UPA the amplitude of the circularly polarised wave rotates in the opposite sense.  

4. Trigrams symbolize binary numbers

In the binary number system, Arabic numerals are represented by their binary counterparts. A binary number can be represented by any sequence of bits (binary digits), which in turn may be represented by any mechanism capable of being in two mutually exclusive states. Binary numbers are commonly written using the symbols 0 and 1. The binary forms of the integers 0, 1, 2, … 7 are:  

0 1 2 3 4

0 1 10 11 100

7

5 6 7

101 110 111

Any positive integer N is a linear combination of successive integer powers of 2:

where c_n = 0 or 1. The binary digits making up the binary form of an integer are the coefficients c_n with the rule that the digit at the extreme right of the binary number is c₀, the one to the left next to it is c₁, etc. The binary digit at each position has two possible values: 0 or 1. Compare this property with the trigrams as combinations of yang or yin lines. Making the identification:

yang line		=	0
yin line		=	1

(for clarity, binary numbers are written henceforth in red) and defining the convention that the line at the base of a trigram corresponds to the binary digit to the far right of its binary number representation, the binary numbers symbolized by the eight trigrams and their equivalent

Arabic numerals are shown in Fig. 11. Notice that the same set of numerals would have resulted by identifying a yang line with 0 and a yin line with 1. As the numbers to be discussed later turn out to correspond to equal numbers of yin and yang lines, as the balance of yang and yin in Nature and Bohr’s Complementarity Principle would lead one to expect, the conclusions that will be drawn do not depend upon which identification scheme is correct. However, Figure 1 indicates that the traditional ordering of the trigrams starts with the Heaven trigram comprising three yang lines and ends with the earth trigram consisting of three yin lines. As the spiritual realms are the origin of the physical world, it is, intuitively speaking, more correct to assign the first number 0 to the Heaven trigram and the last number 7 to the Earth trigram rather than the reverse. This means that the binary number 0 must correspond to the yang line and the binary number 1 must correspond to the yin line, as shown above.  

Associated with each pair of trigrams in a hexagram is a corresponding pair of the integers that they represent. Figure 12 shows their sums. They range from 0 (the sum of the two Heaven trigrams in the top left-hand corner) to 14 (the sum of the two Earth trigrams in the bottom right-hand corner). The integers along the diagonal of the 8×8 square array of integers are even because each is a sum of identical integers, the diagonal hexagrams being composed of like trigrams. Integers in the same column in successive rows increase by 1. The sum of the 64 integers is 448 = 2⁶ + 2⁷ + 2⁸, which has the binary representation 111000000. The sum of the eight diagonal integers = 56 and the sum of the two sets of 28 integers that are off the diagonal = 448 – 56 = 392, i.e., each set adds up to 196. This is also the sum of the 28 integers on the boundary of the array. The sum of the (64-28=36) integers inside the boundary = 448 – 196 = 252. This is the same as the sum of the 36 integers forming one diagonal half of the I Ching  

8

array. The sum of the six internal, diagonal integers = 42, so that the sum of the (36–6=30) internal, off-diagonal integers = 252 – 42 = 210. The superstring and astronomical significance of some of these numbers will be discussed later.

5. Encoding of superstring structural parameters 168 & 336

The seven integers 1–7 can be paired in 21 different ways. The sum of these combinations is 168. The pairs of integers correspond to the 21 pairs of trigrams on either side of the diagonal of the I Ching table that are enclosed in the black or white triangles shown in Fig. 13. So 21 hexagrams on each side of the diagonal encode the number 168, which, according to Section 4, is the number of circularly polarised oscillations made by each whorl as it twists through 180°. This is summarised in Table 1. The outer and inner halves of the UPA are the counterpart of the yang/yin duality, just as the right-handed, positively charged UPA and the left-handed, negatively charged UPA are another manifestation of the yang and yin aspects of matter. The sum of the 22  

9

Table 1

The number values of the 64 hexagrams. The sum of the 21 integers on either side of the diagonal in a black or white triangle is 168. This corresponds to the 168 circularly polarised oscillations made during half a revolution of an outer or an inner segment of each whorl of the UPA. The sum of the 22 integers outside the triangles is 84, which is the number of such oscillations made during a quarter-revolution of a whorl.  

 

 

 

10

integers outside both triangles is 84, which is the number of oscillations made by a whorl during one quarter of a revolution around the spin axis of the UPA. We find that the numbers of oscillations made in one revolution (336), in one half-revolution (168) and in one-quarter revolution (84) of each whorl of the UPA are encoded in the I Ching table of hexagrams symbolising binary number representations of the integers 0–7. This confirms the archetypal nature of the venerable Chinese diagram.  

The numbers 84 and 336 are good examples of the author’s Tetrad Principle⁶ because

84 = 1² + 3² + 5² + 7²,

that is, 84 is the sum of the squares of the first four odd integers, whilst

336 = 4×84 = 2² ×(1² + 3² + 5² + 7² )

                = 2² + 6² + 10² + 14²,

i.e., 336 is the sum of the squares of four even integers spaced 4 units apart, starting with 2² = 4. Notice also that the number of yang and yin lines in the eight trigrams = 24 = 1×2×3×4 and that the number of hexagrams in the I Ching table = 64 = 4³.  

The number of yang and yin lines in the I Ching matrix = 64×6 = 384. The number of lines of each type = 192. The number of lines in the eight diagonal hexagrams = 6×8 = 48. The number of lines in the 56 off-diagonal hexagrams = 384 – 48 = 336.

There are 168 lines in the 28 hexagrams on either side of the diagonal. They comprise 84 yang lines and 84 yin lines. As each whorl makes 84 circularly polarised vibrations during one-quarter of its revolution, each resulting from two plane waves oscillating 90° out of phase, the latter represent the yang and yin phases of a cycle that is half of a larger cycle of 168 oscillations made as the whorl winds through half a revolution (Fig. 13).

The number of lines and broken lines making up the 28 hexagrams on the boundary of

11

the I Ching matrix is 6×28 = 168. The square is the ancient symbol of the four elements of Earth, Water, Air and Fire. The twelve odd integers 3, 5, … 25 arranged on the sides of a square, four per side, add up to 168 (Fig. 14). This parallelism between the properties of

numbers in the context of the geometrical symbol of the number 4 demonstrates its profound role in determining numbers of universal significance — in this case the superstring structural parameter 168.  

The number of circularly polarised waves in a whorl as it makes 2½ outer revolutions and 2½ inner revolutions is 1680. The number of waves 

in each half is 840 (Fig. 15). As a remarkable arithmetic counterpart to the 28 hexagrams on the boundary of the I Ching matrix with 168 lines and broken lines, the sum of the 28 odd integers that can be arranged along the boundary of a square, eight per side, is 840 (Fig. 16).  

12

6. The I Ching table as the Chinese Tree of Life

At the heart of the Jewish mystical tradition called ‘Kabbalah’ is the Tree of Life, or Otz Chiim. It is a representation of Adam Kadmon, or Heavenly Man, the divine prototype or archetypal blueprint governing the nature of God. His ten divine qualities, or Sephiroth, are symbolized by spheres or circles and connected by 22 Paths. They are arranged in space on the three vertical pillars of the tree 

(Fig. 17). The pillars do not lie in the same plane because the tree is a three-dimensional network of lines, some of which cross over one another, as indicated in Fig. 17 by the broken lines. The Sephiroth Chokmah, Chesed and Netzach lie on the right-hand Pillar of Mercy, Binah, Geburah and Hod are on the left-hand Pillar of Severity and Kether, Tiphareth, Yesod and Malkuth lie on the central Pillar of Equilibrium. The so-called ‘invisible Sephirah’ Daath (the circle with a broken line shown in Fig. 17) appears to lie on the central pillar halfway between Kether and Tiphareth. Actually, Daath hovers in front of it because it is not connected by Paths and only does so when it becomes Yesod of the next higher overlapping tree and this Sephirah lies in front of the plane containing the side pillars, whereas the path joining Kether and Tiphareth projects behind this plane. Each Sephirah is negative, or  

13

receptive, to the preceding one and positive to, or having an influence on, the following one. Metaphysically and psychologically speaking, the Sephiroth on the Pillar of Mercy embody dynamic, active, creative aspects of the divine life, those on the Pillar of Severity manifest introspective, passive and nourishing qualities, whilst the Sephiroth on the middle pillar represent the harmony or balance of these complementary qualities. The kinetic energy of a dynamical system subject to conservative forces for which the Law of Conservation of Energy applies is not necessarily constant but changes into potential energy. Kinetic energy — the yang aspect of the system, as discussed in Section 1 — is an attribute of the Pillar of Mercy and potential energy — its yin aspect — is a quality of the Pillar of Severity. One of the titles of Chokmah, which heads the Pillar of Mercy, is ‘Abba’ (the Supernal Father) and Binah heading the Pillar of Severity has the title “Aima” (the Supernal Mother). These titles demonstrate that the male and female aspects of God manifest equally in the side pillars of the Tree of Life. The yang or active, outgoing aspect is expressed in the Pillar of Mercy and the yin or reflective, ingoing aspect is realised in the Pillar of Severity. The Tao is the balance of these complementary opposites. It corresponds to the central Pillar of Equilibrium.  

Figure 18 depicts how the Tree of Life is formed from the centres and points of intersection of four identical circles. The circle of the Tai Chi symbol has a diameter that is four times their radii. The black and white circles in the yang and yin halves coincide with Daath and Yesod of the Tree of Life.  

Earlier work⁷ by the author has shown that the geometry of the Tree of Life — its outer form — implies a geometrical structure within it that has been unrecognised hitherto by Kabbalists. This inner form of the Tree of Life consists of two similar sets of seven regular polygons. They are the triangle, the square, the pentagon, the hexagon, the octagon, the decagon and the dodecagon. The 14 polygons share one side. Figure 19 shows both forms of the Tree of Life superimposed on each other. As the outer form is three-dimensional, what is depicted is its projection onto the plane containing the two sets of polygons. The left-right symmetry of the outer form of the Tree of Life generates a similar symmetry in its inner form: one set of polygons is the mirror image of the other set, with their shared edge extending from Daath to Tiphareth (actually, their projection onto the polygonal plane). This is how Nature’s yin/yang polarity manifests in the inner form of the Tree of Life.

 The symbol of the tetractys at the heart of the number philosophy of Pythagoras:

 

14

15

embodies sacred geometry like the Tree of Life with numbers characterizing how this blueprint becomes actualized in the universe. This is achieved by converting the triangular sectors of each polygon into tetractyses. This turns them into various numbers — the population of dots making up each one. Information about actual manifestations of this cosmic blueprint is encoded numerically in the geometry of both its outer and inner forms. The same information has analogous encodings in subsets of the seven regular polygons. The most obvious example of this is the two sets of the first six polygons (Fig. 20). The twelve polygons have 50 corners. 48 of them are outside their shared edge, 24 per set. The number of dots in the (6+6) polygons is 384, that is, there are (384–48=336) dots other than their external corners. This means that 48 dots (24 on each side of their shared side) are needed to shape through their corners the two sets of polygons made up of 336 dots, each set containing 168 dots. Compare these properties of the inner Tree of Life with the fact that the I Ching table comprises 48 lines and broken lines in its diagonal hexagrams (24 yang lines and 24 yin lines) and 28 hexagrams on either side of the diagonal with 168 yang lines and 168 yin lines. The number (192) of dots in one set of polygons is equal to the number of yang lines in the I Ching table and the number of dots in the similar set on the other side of the shared edge is equal to the number of yin lines, whilst the number of corners on each side is the same as the number of yin or yang lines in the diagonal hexagrams. This remarkable equivalence exists because the I Ching table is, as Chinese tradition states, a representation of the Tao — reality — and so it encodes the superstring structural parameters 168 and 336 in a fashion analogous to how the inner Tree of Life does this.  

The Kabbalistic names of the Sephiroth, their Godnames, Archangels, Orders of Angels and Mundane Chakras can be converted into numbers through the ancient practice of gematria, whereby the number value of a word is the sum of its letter values. This system of 50 numbers represents a complete prescription of the properties of the outer and inner forms of the Tree of Life as the universal blueprint. This prescription applies

16

also to certain subsets of the seven polygons. For example, Yahweh, the Godname of Binah with number value 26, prescribes the set of the first six polygons, which have 26 corners, and Elohim, the Godname of Binah with number value 50, prescribes both sets of polygons, which have 50 corners. They have 48 corners outside their shared edge and 48 is the number value of Kokab, the Mundane Chakra of Hod. 168, the number of dots associated with each set of six polygons other than their corners, is the number value of Cholem Yesodoth, the Hebrew name of the Mundane Chakra of Malkuth. That it is not just coincidence that the Sephirah signifying physical reality should aptly have a Mundane Chaka whose number value characterizes the structure of a superstring can be confirmed by looking at the populations of dots in the six polygons (Fig. 21).

The number value 78 of the word ‘Cholem’ is the number of dots in the triangle, pentagon and octagon, and the number value 90 of the word ‘Yesodoth’ is the number of dots in the square, hexagon and decagon. It is highly improbable that the number values of both words should coincide with dot populations of whole groups of polygons. This view is strengthened by the fact that, of the 168 yin/yang lines on the boundary of the I Ching square, 90 lines (coloured blue in Fig. 21) are on two of its adjacent sides and 78 lines

17

(coloured red) make up the remainder of the hexagrams on the boundary. This remarkable correlation between the properties of geometrical figures belonging to the mystical traditions of two different cultures indicates their transcendental origin.  

The number 168 is embodied in not only the first six polygons but also the seventh polygon — the dodecagon. Dividing its 12 sectors into three triangles and then converting them into tetractyses generates 169 dots other than the 12 corners of the dodecagon. Associated with each dodecagon are 168 dots (Fig. 22). The next type of transformation of the seventh polygon yields just as many new dots as the first kind does for the first six polygons.

The two sets of the first six polygons have 168 dots on their boundaries outside the shared edge (Fig. 23), that is, 168 dots are needed to delineate the shapes of the 12 polygons. This demonstrates in a clear way the shape-defining character of this number, which is realised in the subquark superstring as the number of turns in the closed helix of a whorl as it revolves through 180°. The I Ching counterpart of this property is shown in Fig. 14 as the 168 yin and yang lines of the 28 hexagrams on the boundary of the I Ching pattern.  

When the outer form of the Tree of Life is projected onto the plane containing its inner form so that the central edge shared by the polygons coincides with the line joining Daath to Tiphareth, one finds that Chokmah and Binah coincide with the uppermost corners of the two hexagons,

Chesed and Geburah coincide with the exterior corners of the two triangles and Netzach and Hod are located at the lowest corners of the two hexagons (Fig. 24). Six of the 70 corners of the two sets of seven polygons therefore coincide with positions of Sephiroth on the side pillars. This leaves 64 corners, of which two are the endpoints of the shared edge and 62 are truly new geometrical degrees of freedom. The upper endpoint coincides with the non-Sephirah Daath, meaning ‘knowledge.’ Just as the seven Sephiroth of Construction emerge from the Abyss of Daath separating the objective aspect of God from the subjective Godhead, so each hexagram emerges with each corner of the polygons, starting from the pair of Heaven trigrams and finishing the combinatorial cycle with the pair of Earth trigrams. The   

18

first and last hexagrams play the role of the endpoints of the root edge. The two sets of 31 corners correspond to the two ways of stacking a pair of trigrams. The number value of the Godname El (meaning ‘God’), which is assigned to Chesed, the first Sephirah of Construction, is 31. This is the number of hexagrams other than the first and last ones in each half of the I Ching table. The number 64 is the number value of Nogah (‘glittering splendour’), the Mundane Chakra of Netzach, and 62 is the number value of Tzadkiel (‘Benevolence of God’), the Archangel assigned to Chesed.  

There are 168 yin/yang lines in the 28 hexagrams on either side of the diagonal set of eight hexagrams comprising 48 such lines. The number of lines in the (28+8=36) hexagrams forming a complete half of the I Ching table = 168 + 48 = 216. The number 36 (=6²) is the number value of the Godname Eloha assigned to Geburah, the sixth Sephirah, whose number value is 216 = 6³ . In conformity to the restrictive nature of this Sephirah, its Godname delineates the set of 36 distinct hexagrams, the 28 others being just those on the other side of the diagonal with their trigrams stacked in reverse order.  

Given that the eight trigrams can be regarded as symbolic binary representations of the integers 0–7 and that the Kabbalistic system of Godnames, etc define aspects of the I Ching table, it should not be very surprising that Yahweh (יהוה) — the most well-known Godname — has a simple representation in terms of binary numbers. Its number value is 26, which is the sum of the powers of 2 in the following tetractys array:  

26 =	20	=	1	=	1
	21  20		1 1		3
	22  21  20		1 1 1		7
	21  22  21  20		1 1 1 1		15

Each row comprises successive powers of 2, starting with 2⁰ = 1. Remarkably, the number value 26 of the Godname of Chokmah, expressing the creative aspect of God, is the sum of the four odd integers 1 = 1, 3 = 11, 7 = 111 & 15 = 1111. These integers are known in mathematics as the first four Mersenne* numbers, the nth Mersenne number being defined as M_n = 2ⁿ – 1. Notice also that the fourth Mersenne number M₄ = 15 is the sum of the first four powers of 2 representing the lowest row of the tetractys and expressed by the binary number 1111. This is the number value of Yah (יה), the older version of the Divine Name Yahweh. It is the number of hexagrams forming two adjacent sides of the I Ching square. Yah therefore prescribes the eight-fold size of the square array of hexagrams. It also defines the number of its hexagrams because  

64 = 8² = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15.

The number of hexagrams inside the table in one triangular half of it is 21. This is the number value of Ehieh (AHIH), the Godname assigned to Kether, the first Sephirah. They are made up of (21×6=126) yin/yang lines. Remarkably, 126 is the sum of the four types of combinations of the letters A, H and I in AHIH:  

A = 1, H = 5, I = 10

1. 2. 3. 4.	A + H + I AH + HI + AI + HH AHI + HIH + AHH AHIH	= = = =	16 42 47   21
	TOTAL	=	126

________________________
* Named after Father Marin Mersenne, who was a natural philosopher, theologian, mathematician, musical theorist and friend of Descartes, Fermat and Pascal.

19

The remaining number of yin/yang lines in the I Ching table = 384 – 126 = 258. This is the 129th even integer. This shows how Yahweh Sabaoth, the Godname of Netzach with number value 129, prescribes the table. Yah defines 15 hexagrams lying on two adjacent sides of the square, leaving 13 hexagrams with 78 yin/yang lines on the other two sides. The number of yin/yang lines in the I Ching square other than these = 384 – 78 = 306. This is the 153rd even integer. It shows how Elohim Sabaoth, the Godname of Hod with number value 153, prescribes the table (see also Fig. 43).  

In his Timaeus Plato described how the demiurge measured the World Soul with the harmonic proportions of the musical scale by dividing a strip of its substance into portions measured by the numbers forming two geometric series of four terms each: 1, 2, 4, 8 and 1, 3, 9 and 27 (Fig. 25). Article 11 discussed the way in which these numbers when seen as part of a tetractys of ten numbers generates the tone ratios of the Pythagorean musical scale. Their sum is 90, which is the number of yin/yang lines in the 15 hexagrams on two adjacent sides of the I Ching square prescribed by the Godname Yah. In terms of the equivalence of the tetractys and Tree of Life as representations of the ten-fold nature of God, the dot at the centre of the tetractys corresponds to Malkuth, the Sephirah denoting the physical world, symbolized by the planet Earth. In the Lambda tetractys, this number is 6. This is the number of yin lines in the

pair of Earth trigrams, which is the last of the hexagrams on adjacent sides of the I Ching square (shown in Fig. 26 in red). The sum of the remaining nine integers is 84, where  

84 = 1² + 3² + 5² + 7² .

This is the number of yin/yang lines in the remaining 14 hexagrams. The sum of the integers at the corners of the hexagon in the Lambda tetractys is 48. This is the number of yin/yang lines in the eight hexagrams at the top of the square expressing the integers 0, 1, 2, 3, 4, 5, 6 and 7. The sum (36) of the integers at the corners of the tetractys is the number of remaining yin/yang lines. Symbolically, the integer 6 at the centre of the tetractys defines the number of lines and broken lines in a hexagram, whilst the sum of the integers 1, 8 and 27 at the corners of the Lambda is the number of hexagrams in a diagonal half of the square.

20

7. Encoding of planetary distances in the I Ching table

It was shown in Article 17 that the assumption that the primordial planetary nebula giving birth to the Solar System had the geometry of a logarithmic spiral explains why the first eight planets conform to the Titius-Bode Law. In accordance with the eightfold pattern often found in nature, namely, the eight notes of the musical scale, the octets of quarks and the eight-fold periodicity of elements in the chemical periodic table, it was hypothesized that the spiral geometry of the planetary nebula had the fractal-like quality of being re-scaled for every set of eight

Table 2. Wavelengths of the Pythagorean musical undertones.

C	D	E	F	G	A	B	Number of sub-harmonics
1	8/9	64/81	3/4	2/3	16/27	128/243	0
2	16/9	128/81	3/2	4/3	32/27	256/243	1
4	32/9	256/81	3	8/3	64/27	512/243	3
8	64/9	512/81	6	16/3	128/27	1024/243	5
16	128/9	1024/81	12	32/3	256/27	2048/243	7
32	256/9	2048/81	24	64/3	512/27	4096/243	9
64	512/9	4096/81	48	128/3	1024/27	8192/243	11
128	1024/9	8192/81	96	256/3	2048/27	16384/243	13
256	2048/9	16384/81	192	512/3	4096/27	32768/243	15
512	4096/9	32768/81	384	1024/3	8192/27	65536/243	17
1024	8192/9	65536/81	768	2048/3	16384/27	131072/243	19

planets that condensed out of it. This means that, as well as being the last member of the first octet of planets, Uranus is also the first member of the second octet, the asymptotic centre of the rescaled spiral being centred on its orbit. In terms of a (1/10 A.U.), the mean distance of the nth planet after Mercury in the first octet from the first asymptotic centre is:  

dn = (3/2)×2na

(n = 1–8)

and the mean distance of the n'th planet after Uranus in the second octet from the second asymptotic centre (that is, from Uranus) is:

Dn' = (3/2)×2n'a

(n' = 1–8)

The mean distance of Uranus (n = 7) from the first asymptotic centre is

d₇ = (3/2)×2⁷ = 192a

and the mean distance of Pluto (n' = 2) from Uranus is

D₂ = (3/2)×2²a = 192a.

The predicted mean distance of Pluto from the Sun is 38.8 A.U., which compares well with the measured value of 39.48 A.U.

21

Table 2 above shows that 384 is the 16th sub-harmonic, so that it is the last of the sub- harmonics in the 4×4 square array:

2 8 32 128

3 12 48 192

4 16 64 256

6 24 96 384

Also,

384 =

4! 4! 4! 4!

4! 4! 4! 4!

4! 4! 4! 4!

4! 4! 4! 4!

(4! =1×2×3×4)

These properties are illustrations of the author’s Tetrad Principle, proposed in Article 1,⁸ according to which integers that have cosmic significance because they parameterize holistic systems like the Solar System and the superstring are always defined mathematically by the first four integers: 1, 2, 3 & 4, or by the number 4, or tetrad, as either the fourth or sixteenth of a class of numbers or as the sum of a 4×4 square array of numbers that mathematically relate to the tetrad, such as 4!. The 64 hexagrams are an example of the lattermost because 64 is the sum of the 16 integers 4 arranged in a 4×4 square array.

A decagon divided into tetractyses contains 61 dots, 30 lying on its boundary and 31 in

22

its interior. This property correlates with the fact that the tone ratio 384 of the perfect fifth of the ninth octave is the thirtieth overtone and the 61st note (Fig. 27). In other words, if the tone ratio 1 of the tonic of the first octave is assigned to the centre of the decagon, the 30 notes up to 384 with fractional tone ratios can be assigned to the dots inside the decagon and the 30 overtones up to 384 can be assigned to dots lying on its boundary. This illustrates the Pythagorean title “All Perfect” assigned to the number 10 represented by the decagon, for it indeed generates through the musical tones of the Pythagorean scale the number 384 as the number of yin and yang lines in the I Ching table and as the mean distance of Pluto from the first asymptotic centre of the logarithmic spiral-shaped planetary nebula that spawned the ten members of the Solar System. The Godname El (לא) of Chesed with number value 31 prescribes the number 384 because this is the tone ratio of the 61st note, where 61 is the 31st odd integer.

It was pointed out in Section 5 that 168 dots other than corners are associated with the first six polygons of the inner form of the Tree of Life. The two sets of polygons have 50 corners and 2×168 = 336 dots, a total of 386 dots. Of these, two are the endpoints of the shared edge,

leaving 384 dots, 192 dots being associated with each set of six polygons. The predicted mean distance of the last planet Pluto from Uranus is 192a — the same as the mean distance of Uranus from the first asymptotic centre (Fig. 28). Therefore, Uranus is midway between Pluto and this centre. In terms of the unit of distance a, exactly the same division:  

384 = 192 + 192

exists between the mean distances between Pluto and Uranus and between Uranus and the first asymptotic centre as that between the dots in the two sets of polygons. This demonstrates explicitly the Tree of Life nature of the Solar System. Table 2 indicates that 192 is the wavelength of the perfect fourth of the eighth octave of undertones and 384 is the wavelength of the perfect fourth of the ninth octave — the next higher octave. It shows the analogy between the musical sounds of the scale and the picture of the Solar System made up of planets belonging to two octets. In fact, the wavelengths of successive perfect fourths of the undertones:  

3, 6, 12, 24, 48, 96, 192

(shown highlighted in purple in Table 2) are just the distances (in terms of a) of the first seven planets after Mercury from the asymptotic centre predicted by the logarithmic spiral theory of the Titius-Bode Law.

The same 192:192 division is displayed in the I Ching diagram (Fig. 29). The 64 hexagrams have 6×64 = 384 lines and broken lines, that is, 192 of each type. The uppermost row of eight trigrams consists of 24 yin/yang lines. The first row of

23

24

hexagrams has 48 yin/yang lines (24 of each type), that is, 24 more lines. According to Table 13 in Article 17, the average distance (in units of a) of the Asteroid Belt from the first asymptotic centre is 24, whilst the mean distance of Jupiter from this centre is 48, that is,

24 units further out. The first two rows of hexagrams have 96 lines. 96 is the distance of Saturn from the centre. The first four rows have 192 lines. 192 is the distance of Uranus from the centre. All eight rows of hexagrams have 384 lines, and 384 is the distance of Pluto from the centre. Its mean distance from Jupiter = 384 – 48 = 336, which is the number of yin/yang lines in the off-diagonal hexagrams of the I Ching diagram, the diagonal hexagrams having 48 lines. This famous divinatory diagram can  

25

therefore be said to represent the Solar System in that, as they double in number, the populations of yin and yang lines in the rows of hexagrams measure the distances of successive planets from the asymptotic centre of the logarithmic spiral from which they were born (Fig. 30). This distance is given by the Titius-Bode Law:

d_n= 3×2^n-1,

where n = 1 for Venus, n = 2 for Earth, etc. To understand the way in which the I Ching table encodes planetary distances, one has, firstly, to read across the first row of trigrams, starting with the Heaven trigram, and taking subsets that double in size. The number 3 in the Titius-Bode Law denotes its number of yang lines. Therefore, the Heaven trigram defines the mean distance of Venus from the asymptotic centre. Then the first two trigrams have six lines. They correspond to Earth (n=2), whose mean distance from the centre is six units. Next, the first four trigrams have 12 lines. They define the mean distance of Mars (n=3) from the centre. All eight trigrams have 24 lines, which define the mean distance 24 of the Asteroid Belt (n=4) from the centre.  

Having counted the first row of trigrams, one proceeds to count downwards, now doubling the number of rows each time. The first row of hexagrams has 48 lines, which defines the mean distance of Jupiter (n=5) from the centre. The first two rows have 96 lines, which defines the mean distance of Saturn (n=6) from the centre. The first four rows comprise 192 lines, which defines the average distance of Uranus (n=7) from the centre. This completes the first octet of planets. Uranus is at the asymptotic centre of the second, re-scaled octet of planets whose distances from this centre are given by⁹

D_n’= 96×2^n'-1,

where n = 1 for Neptune and n = 2 for Pluto. Instead of counting two, four and eight trigrams again, the re-scaling means that the first four rows of hexagrams replaces the Heaven trigram and we commence counting two rows of hexagrams with 96 lines. These define the average distance 96 of Neptune from the second asymptotic centre, that is, its distance from the first

asymptotic centre (its true Bode number) = 196 + 92 = 288. Then we count four rows of hexagrams with 192 lines, which define the distance 192 of Pluto from the second centre. This means that its average distance from the first asymptotic centre (its actual Bode number) = 192 + 192 = 384.

The four successive powers of 2 in the Platonic Lambda:

2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8,

express this doubling of successive planetary distances from the asymptotic centre Similarly for the analogous progressive doubling of lines in the I Ching table. The

26

doubling stops at the fourth term in the geometric series, which defines both the eight trigrams, the first eight rows of trigrams making up 

the first half of the I Ching table and all eight rows of hexagrams — an illustration of the Tetrad Principle at work. 192 — the distance from the asymptotic centre of the last member of the first octet of planets and the number of yang or yin lines in the I Ching table — is the wavelength of the perfect fourth of the eighth octave of undertones, where 8 is the fourth even integer. In musical terms, the Heaven trigram can be regarded as the octave of the Pythagorean musical scale and the 128 trigrams of the I Ching table span a musical octave ending in the pair of Earth trigrams of the sixty-fourth hexagram — the lowest note of the eight-fold scale.  

27

128 is the tone ratio of the eighth octave and the fiftieth tone or undertone in the Pythagorean scale, showing how Elohim, the Godname of Binah with the number value 50, prescribes this number. The sum of the binary values of the 28 hexagrams on the boundary of the table (Table 1) is 196. This is the distance of Uranus from the Sun predicted by the logarithmic spiral theory.¹⁰ The boundary of the table encodes not only the superstring structural parameter 168 but also the scale of the first planetary octet.  

It is fitting that the number value of Nogah, the Mundane Chakra of Netzach, the seventh Sephirah, is 64, for it is the number of hexagrams resulting from the seventh doubling up (see Fig. 30). It is also fitting that the number value of Kokab, the Mundane Chakra of Hod (the eighth Sephirah) is 48, for this is the number of yin/yang lines in the eight hexagrams of any row of the I Ching table. That the pattern of 64 hexagrams unfolding in the table is Kabbalistically complete is confirmed by the fact that 64 Sephirothic emanations are needed to create ten overlapping Trees of Life, that is, a Tree of Life differentiated by having each Sephirah represented by a Tree of Life (Fig. 32).

As Fig. 24 indicates, there are 64 corners of the polygons making up the inner form of the Tree of Life that do not coincide with the positions of Sephiroth on the side pillars, that is, 64 new, geometrical degrees of freedom intrinsic to this inner form shape its growth out of what the author calls the ‘root edge’ shared by the polygons.  

In Article 11,¹¹ the Lambda tetractys was generalised to a tetrahedron of which it is the first face. The fourth face is a tetractys array of integers the ratios of which define the tone ratios of the perfect fourths, perfect fifths and octaves of the Pythagorean musical scale. The sum (350) of its twenty integers is the number of corners of the ten sets of seven polygons enfolded in ten overlapping Trees of Life. Fig. 33 indicates that its largest integer is 64. It further illustrates how this number characterizes archetypal objects such as the inner Tree of Life, ten Trees of Life and the I Ching table. In fact, the geometric series of integers 8, 16, 32 and 64 lining an edge of the fourth face denotes the number of hexagrams in, respectively, one, two, four and eight rows of the table.

8. Octonions and the I Ching table

We found earlier that the geometric terms 1, 2, 4 and 8 in the Platonic Lambda define the number of trigrams in the four stages of the building of the row of eight trigrams and the factors by which the rows of hexagrams build up into the I Ching table. Mathematicians have known for many years that there are four — and only four — classes of normed, real division algebras. They are the 1-dimensional real numbers, the 2-dimensional complex numbers, the 4-dimensional quaternions and the 8-dimensional octonions, or Cayley numbers.  

An octonion has the form:

28

N = a₀ + a₁e₁ + a₂e₂ + a₃e₃ + a₄e₄ + a₅e₅ + a₆e₆ + a₇e₇,

where the a_i (i = 0, 1, 2, 3, 4, 5 6, 7) are real numbers, the unit octonions e_i (i = 1–7) are imaginary numbers:

ei2 = -1

(i = 1–7)

and are anticommutative in their multiplication:

eiej = -ejei

(i ≠ j)

Shown below is the multiplication table for the 8-tuple of unit octonions: (1, e₁, e₂, e₃, e₄, e₅, e₆, e₇):

Table 3. The octonion multiplication table.

Unlike the I Ching table, which has 64 different pairs of trigrams symbolising in binary form the 15 different integers 0–14 created by adding together the values of pairs of trigrams, Table 3 has 16 different entries: 1, -1, and ±e_i.  

As the realisation of the most general type of numbers showing neither associativity nor commutativity, the eight unit octonions are the mathematical counterpart to Daath and the seven Sephiroth of Construction. Their correspondence with the eight trigrams is set out below:

We saw in Section 15 that the sum of the values of the 42 off-diagonal hexagrams whose trigrams express the numbers 1–7 is 336, the 21 values on either side being 168. These values are the sums of the pairs of hexagrams. If the rule is imposed that addition should be modulo 8, the sum of the 49 integers in the new table is 168, the number value of Cholem Yesodoth, Mundane Chakra of Malkuth. This shows how El Chai, the Godname of Yesod with number 49, prescribes this structural parameter of superstrings. That this is not coincidence is indicated by the fact that the number values 90 and 78 of, respectively, Yesodoth and Cholem are the sum of the first three rows and the sum of the last four rows of the table of new numbers (Fig. 34). This reflects the fact that the sum of the original 49 integers, of which 28 are greater than or equal to 8, is  

29

392, so that addition modulo 8 yields the number 392 – 28×8 = 168.

The Godname Ehieh assigned to Kether with number value 21 prescribes the superstring structural parameter 168 because it is the sum of the 21 different pairs of integers that can be selected from the set of integers 1–7.

There are seven 3-tuples e_i, e_i+1 and e_i+3, where the index is defined modulo 7. They are represented by the Fano projective plane (Fig. 35). It generates the multiplication table for the seven imaginary, unit octonions when they are assigned to its points in the way shown in Fig. 35. The multiplication of two octonions is the third on the same straight or curved line provided that their multiplicative ordering follows the arrows

          

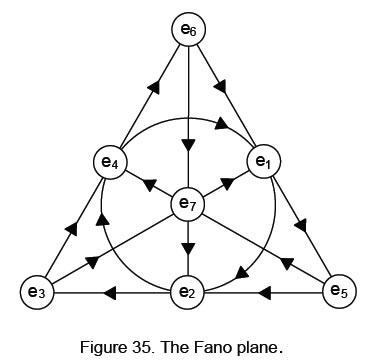
on the line. Their product is minus the third if multiplication is opposite to the sense of the arrow. Although the Fano plane is no more than a mnemonic, the diagram is simply connected to the generation of the Tree of Life from similar circles that overlap centre to circumference (Fig. 36). The three lines inside the triangle are paths of the Tree of Life. The circles generate the internal contour of the Tai Chi. When the path joining Chesed

30

and Geburah is extended to cut the circle of the Tai Chi, a square constructed on this extension and its upper edge extended back to intersect the vertical line along the Pillar of Mercy, the rectangle formed by the vertical and horizontal lines is a Golden Rectangle. The Golden Ratio is therefore present in the Fano plane when it is centred on Tiphareth (meaning “beauty”) as the focal point of the Tree of Life and the centre of the Tai Chi.  

The Fano plane has the symmetry group SL(2,3) — the special linear group of 3×3 invertible matrices with determinant 1 over the field (1, -1). It is isomorphic to PSL(2,7), the projective special linear group. This is the automorphism group of the Klein Quartic equation well known to mathematicians:  

X³Y + Y³Z + Z³X = 0

A Riemann surface with the maximum number of automorphisms is a Hurwitz curve. The Klein curve is the Hurwitz curve with the smallest genus 3.

It has 168 automorphisms. They can be represented by the Klein Configuration (Fig. 37). It has 168 coloured, hyperbolic triangles and 168 grey triangles, each one representing an automorphism. Each of its seven identical sectors comprises two slices containing 24 coloured triangles and 24 grey triangles. One slice comprises four red triangles, four yellow triangles and four green triangles. The other slice three yellow red triangles, three yellow triangles, three green triangles and three blue triangles. The seven former types have 28 red, 28 yellow and 28 green triangles, that is, 28 sets of a red, blue and green triangle. The Klein Configuration is therefore made up of 28 triplets of a red, blue and green triangle, seven triplets of red triangles, seven triplets of yellow triangles, seven triplets of green triangles and seven triplets of blue triangles. In other words, it comprises 28 triplets of one kind (one red, one yellow, one green triangle) — a total of 84 triangles — and 28 triplets of four other kinds. The colours codify different types of automorphisms. They comprise 49 red triangles, 49 yellow triangles, 49 green triangles and 21 blue triangles. This shows how the Godnames Ehieh with number value 21 and El Chai with number value 49 prescribe the Klein Configuration.

What is remarkable about this grouping of the 168 coloured triangles into triplets, 28 of one kind with 84 triangles and 84 of four other kinds with 84 triangles, is that it correlates with the fact that the I Ching table is composed of triplets of yin/yang lines — trigrams — and that there are 56 trigrams on each side of the diagonal. It is immaterial that not all the coloured triangles cluster in each slice in groups of 3. Instead, what is non-trivial is that the numbers of triangles of each of the four colours are such that they permit natural division into 28 triplets of one kind and 28 triplets of four other types. The coloured triangles correspond to the yin and yang lines in the 28 off-diagonal hexagrams in a half of the table and the grey triangles correspond to the yin and yang  

31

32

lines in the 28 off-diagonal hexagrams in the other half. Figure 38 displays the isomorphism between the features of the I Ching table and the Klein Configuration.

Further evidence that the I Ching table encodes the physics of superstrings is provided by the root structure of the superstring gauge symmetry group E₈. The roots of the E₈ algebra can be described in terms of eight orthonormal unit vectors {u_i}. Eight zero roots correspond to points at the centre of the root diagram and 240 non-zero roots all have length √ 2. They are given by  

The 240 non-zero roots of E₈ comprise 168 made up of four sets of 28 and one set of 56, one set of 70 and two single ones. The 56 permutations of the 8-tuple (1, -1, 0, 0, 0, 0, 0, 0) comprise 28 with the coordinate -1 on the right-hand of the coordinate 1 and 28 with -1 on its left-hand. The 168 permutations therefore comprise six sets of 28. Compare this with the 28 hexagrams on either side of the diagonal in the I Ching table. Figure 23 indicates that they have 84 yin lines and 84 yang lines. Each yin or yang line denotes a simple root of E₈ and a hexagram symbolizes the six types of 8-tuples, the 28 hexagrams reflecting the fact that there are 28 permutations of each type. Here is unambiguous evidence of the connection between the group mathematics of superstrings and the pattern of the ancient I Ching table.  

The division of each of the seven slices of the Klein Configuration into two sets of 12 coloured triangles generates the division 168 = 84 + 84. Its counterpart in the I Ching table is the fact that there are 84 yin lines and 84 yang lines making up the 56 trigrams on side of the diagonal. Similarly, the two sets of 12 grey triangles in each slice have their counterpart in the 84 yin lines and 84 yang lines of the 56 trigrams on the other side of the diagonal. In terms of octonions, it was shown in Article 15¹² that the 12 coloured triangles in one half of a slice correspond to permutations of pairs and triplets of octonions in a 3-tuple (e_i, e_i+1, e_i+3), whilst the 12 coloured triangles in the other slice correspond to the permutations of pairs and triplets of the inverses of octonions in a 3-tuple, namely, (-e_i+3, -e_i+1, -e_i ) (multiplication of inverse octonions operates in the

33

34

opposite sense of the arrows of the Fano plane in Fig. 35). One can formally identify a yang line as an octonion e_i and a yin line as the inverse of an octonion, i.e., -e_i . This is consistent with the intuitive meaning of yang and yin as positive and negative polarity.  

Figure 39 shows the correspondence between the Tree of Life and the Klein Configuration. Associated with the right-hand set of the first six regular polygons are 168 black dots other than their 25 corners. They correspond to the 168 black hyperbolic triangles in the Klein Configuration. Associated with the left-hand set of similar polygons are 168 white dots other than their 25 corners. They correspond to the 168 white triangles. The Divine Name Elohim with number value 50 prescribes the 336 dots because the two sets of polygons have 50 corners.  

As was pointed out in Article 15,¹³ the two sets of 12 coloured triangles in each slice of the Klein Configuration correspond to the 12 permutations of pairs and triplets of each 3-tuple of octonions (e_i , e_i+1, e_i+3) and to the 12 permutations of pairs and triplets of each 3-tuple of their inverses (-e_i+3, -e_i+1, -e_i). The (84+84) permutations of the seven 3-tuples are symbolized by the (84+84) dots on the boundaries of the first (6+6) polygons. As each whorl of the UPA makes 168 circularly polarised oscillations in every half- revolution, 84 of them in every quarter-revolution, each dot also denotes an oscillation. The following equivalence is established:  

Tetractys dot yin/yang line coloured triangle circularly polarised oscillation and 2 sets of six polygons 2 trigrams of hexagram 2 halves of slice ei & (ei) -1 .

The inner form of the Tree of Life, the I Ching and the Klein Configuration representing the group of automorphisms of the Klein Quartic are isomorphic versions of the same pattern, namely, the universal blueprint that determines the nature of all things made in the biblical ‘Image of God’ — whether a superstring or the Solar System.  

In the Pythagorean counterpart of the mystical traditions of Kabbalah and Taoism, the representation of whole (or holistic) systems is the 

tetractys. Its 10 dots symbolize the ten-fold nature of Divine Unity. If one calls it the ‘1st-order tetractys,’ its next higher differentiation is the ‘2nd-order tetractys’ shown in Fig. 40. Its ten tetractyses are composed of 85 dots, where 84 is the sum of the first four powers of 4. This fact is another example of the Tetrad Principle¹⁴ proposed by the author, wherein archetypal patterns or numbers of universal (and therefore scientific) significance are expressed by the number 4. We saw in Section 6 that, when the 70 sectors of the two sets of six polygons are turned into tetractyses, 336 dots are generated that correspond to the 336 yin/yang lines of the two sets of 28 hexagrams on either side of the diagonal of the I Ching. Miraculously, when the 47 sectors of all seven enfolded, regular polygons are  

35

36

37

converted into 2nd-order tetractyses, the number of dots in them is 3360 (Fig. 41), that is, the number of dots in 336 tetractyses. If, therefore, a yin or yang line is considered to symbolize not 0 or 1 but 10, the numerical value of the 56 off-diagonal hexagrams is 3360 — precisely, the same as the number of dots composing the seven polygons! This illustrates the remarkable mathematical unity underlying symbols from the mystical traditions of diverse cultures. The scientific significance of this equivalence is the fact that, because each of the ten whorls of the UPA/superstring makes five revolutions as it oscillates 1680 times, all ten whorls make 16800 oscillations, that is, 3360 oscillations for each revolution. Assigning the number 10 to a yin and yang line in the I Ching table is therefore equivalent to taking into account the ten-fold nature of the superstring as the realization of the ten-fold Tree of Life in the subatomic world. Amazingly, the geometry of the inner form of the latter encodes through the tetractys the very number of helical turns of the ten whorls that define the vibrational state of the superstring constituent of up and down quarks.  

If the number 10 is assigned to a hexagram, the 64 hexagrams of the table add up to 640. This is the number value of Shemesh (“the solar light”), the Hebrew name of the Mundane Chakra assigned to Tiphareth. Indeed, 64 is the number value of Nogah (“glittering splendour”), the Mundane Chakra of Netzach, the Sephirah following Tiphareth. Hod, the next Sephirah, has a Mundane Chakra called Kokab with the number value 48, which is the number of yin/yang lines in a generic row of eight hexagrams. Starting with the Heaven trigram composed of three yang lines, a further 87 trigrams border two sides of the I Ching table with 15 hexagrams prescribed by the Godname Yah. This is the number value of Levanah (“the lunar flame”), the Mundane Chakra of Yesod, which follows Hod in the Tree of Life. Including Cholem Yesodoth (“breaker of the foundations”), which is the Mundane Chakra of the last Sephirah, Malkuth, whose number value 168 is the number of yin/yang lines of the 28 off-diagonal hexagrams, we see that five consecutive Sephiroth of the Tree of Life have Mundane Chakras whose number values aptly and naturally characterize properties of the I Ching table. Assigning 10 to hexagrams gives a sum of 280 to these 28 hexagrams. This is the number value of Sandalphon (“Manifest Messiah”), the Archangel associated with Malkuth. The sum of the eight diagonal hexagrams becomes 80, which is the number value of Yesod, the penultimate Sephirah. As shown in Fig. 20, their 24 yin lines and 24 yang lines correspond to the 24 corners defining the shapes of each set of six polygons embodying the superstring structural parameter 168. In the Klein Configuration, they are the 24 coloured triangles and the 24 grey triangles in each of its seven slices shown in Fig. 37. Between the first hexagram composed of two Heaven trigrams and the last hexagram made up of two Earth trigrams there are 62 hexagrams. This is the number value of Tzadkiel (“Benevolence of God”), the Archangel of Chesed. It is the number of corners of the two sets of seven enfolded polygons constituting the inner form of the Tree of Life that do not coincide with the positions of the Sephiroth when its outer form is projected onto the plane containing the polygons (see Fig. 24).  

The presence of Kabbalistic numbers in the I Ching raises the question of whether it is just chance that the Hebrew Godnames have number values (Fig. 42) that naturally quantify types of hexagrams in the table. Any supposedly more rational explanation that replaces one set of miraculous, numerical correlations by an equally extraordinary series of coincidences is hardly more plausible. The only reason why there are too many Kabbalistic numbers characterizing a 5,000-years old Chinese diagram to be due to chance is that the I Ching is the Chinese counterpart of the Tree of Life blueprint determining the nature of Tao. The only sensible rationale for the remarkable isomorphism between the I Ching table, the Tree of Life and the Klein Configuration  

38

revealed in this article is simple: they are different ways of describing fundamental reality. Despite outward differences in its expression, Divine Truth remains the same whatever the period or culture in which it was mystically revealed.  

References

¹Recently, a physicist called Shahriar Afshar has conducted experiments that seem to contradict the Principle of Complementarity by demonstrating that particles can behave as waves at the same time. His findings await replication and scrutiny by other researchers (see “Quantum Rebel,” by Marcus Chown, New Scientist, 24 July, 2004).

² http://www.chinesefortunecalendar.com/FAQ.htm.

³ A useful commentary on the 64 hexagrams can be found at: http://11members.aol.com/tig550908/i-hexagrams.htm.

⁴ Besant, Annie and Leadbeater, Charles W. Occult Chemistry, 1st ed., Theosophical Publishing House, Adyar, Chennai, India, 1908.

⁵ Phillips, Stephen M. Extra-sensory Perception of Quarks, Theosophical Publishing House, Wheaton, Illinois, USA, 1980; Anima: Remote Viewing of Subatomic Particles, Theosophical Publishing House, Adyar, Chennai, India, 1996; ESP of Quarks and Superstrings, New Age International, New Delhi, India, 1999.

⁶ Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring & Bosonic String Theories,” (WEB, PDF), p. 5.

⁷ Phillips, S.M.The Mathematical Connection between Religion and Science (Antony Rowe, England, 2009).

⁸ Ibid.

⁹ Phillips, Stephen M. Article 17: “The Logarithmic Spiral Basis of the Titius-Bode Law,” (WEB, PDF), pp. 25–26.

¹⁰ Ibid, p. 26.

¹¹ Phillips, Stephen M. Article 11: “Plato’s Lambda — Its Meaning, Generalisation and Connection to the Tree of Life,” (WEB, PDF).

¹² Phillips, Stephen M. Article 15: “The Mathematical Connection between Superstrings and Their Micro-psi Description: a Pointer Towards M-theory,” (WEB, PDF), pp. 10–12.

¹³ Ibid.

¹⁴ Ref. 5.

39