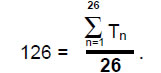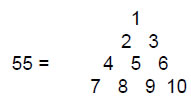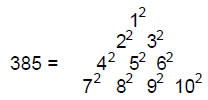ARTICLE 32

by

Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

Abstract

 

 

1. Interval composition of the eight Church musical modes
Article 16¹ analysed the notes and intervals of the eight musical modes used in plainsong by the Roman Catholic Church for hundreds of years. They consist of four ‘authentic modes’: Dorian (D scale), Phrygian (E scale), Lydian (F scale) and

1

Mixolydian (G scale), and four ‘plagal modes’: Hypodorian (A scale), Hypophrygian (B scale), Hypolydian (C scale) and Hypomixolydian (D’ scale). The lattermost is the D scale, but with a different dominant, or reciting note, and a different finalis, or ending note. The C scale is the Pythagorean musical scale, the tone ratios of whose notes are:

1    9/8    81/64    4/3    3/2    27/16    243/128    2

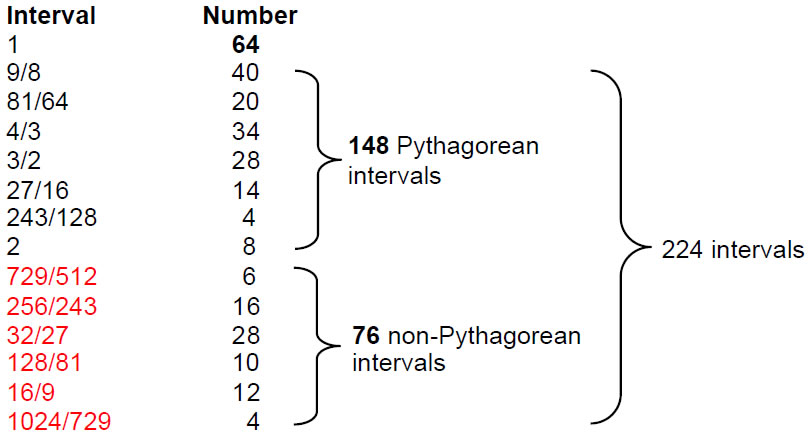
Table 1 lists the numbers of each kind of note/interval found in the Church modes (Pythagorean intervals are those whose size is one of the above tone ratios):

Table 1. Numbers of intervals in the eight Church musical modes.

Fractions written in red denote non-Pythagorean notes. A scale has eight notes with 36 intervals (eight ‘1’s and 28 intervals between the notes). The eight D-D’ scales have (8×36=288) intervals, where 288 = 1¹ + 2² + 3³ + 4⁴. This demonstrates how the Tetrad Principle² determines the total number of intervals between the (8×8=64=4³) notes in the eight scales. They comprise (8×8=64) ‘1’s and (8×28=224) intervals between notes. Eight of these are octaves. The (224–8=216) intervals that are not octaves comprise 140 Pythagorean intervals and 76 non-Pythagorean intervals, showing how YAHWEH ELOHIM, the Godname of Tiphareth with number value 76,³ prescribes the tone intervals of the eight Church musical modes that do not belong to the Pythagorean musical scale. Notice that there are 50 non-Pythagorean intervals of value 729/512 (×6), 256/243 (×16) and 32/27 (×28) and 26 non-Pythagorean intervals of size 128/81 (×10), 16/9 (×12) and 1024/729 (×4). This 50:26 division reproduces the number values of ELOHIM and YAHWEH. 216 is the number value of Geburah, the sixth Sephirah. Therefore, the number value 36 of its Godname ELOHA is the number of intervals in a Church mode and its own number value is the number of intervals other than octaves in all eight modes. 140 is the number value of Masloth, the Mundane Chakra of Chokmah, traditionally called ‘the Sphere of the Zodiac.’ Including the eight octaves, the eight modes have 148 Pythagorean intervals, where 148 is the number value of Netzach, the eighth Sephirah. Of the 288 intervals, eight are octaves, leaving 280 intervals that are not octaves, where 280 is the number value of Sandalphon, the Archangel of Malkuth. There are 64 ‘1’s, where 64 is the number value of Nogah, the Mundane Chakra of Netzach. There are 72 ‘1’s and ‘2’s, where 72 is the number value of Chesed. Hence, the number value 72 of the first Sephirah of Construction measures the number of intervals in the eight Church modes that are ‘1’s or ‘2’s and the number value 216 of the second Sephirah of Construction measures the number of intervals that are not ‘1’s or

2

‘2’! This remarkable prescription by two consecutive Sephiroth of Construction applies to any set of eight scales, whatever the starting one, e.g., the eight C–C’ scales.

The 14 different notes belonging to the eight D–D’ scales are, in order of increasing tone ratios:

1   256/243    9/8   32/27    81/64   4/3    1024/729    729/512    3/2   128/81    27/16   16/9    243/128 2.

These notes make up the seven different musical scales and belong not just to the D–D' scales but to any set of eight scales in which one scale is repeated. Between the tonic and octave are six Pythagorean notes and six non-Pythagorean notes. As the 216 intervals of the eight D–D’ scales that are not ‘1’s or ‘2’s comprise 140 Pythagorean intervals and 76 non-Pythagorean intervals (see above), it means that there are (216–12=204) repetitions of these intervals comprising (140–6=134) Pythagorean intervals and (76–6=70) non-Pythagorean intervals. The 48 notes

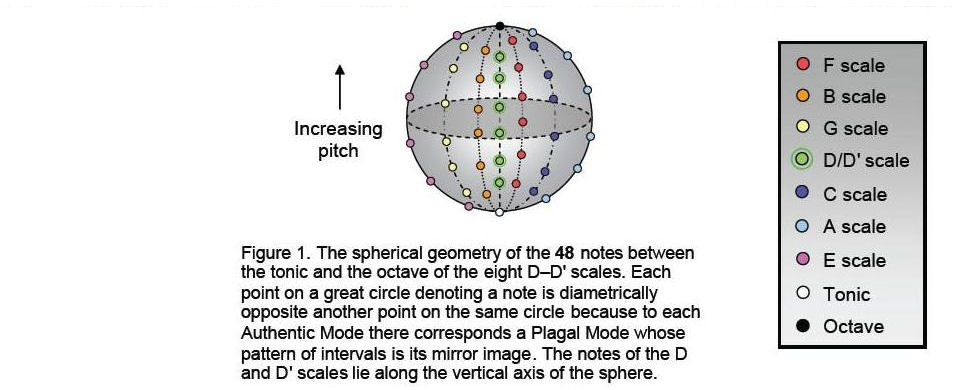
between the tonic and octave of the eight scales can be represented by points on a sphere (Fig. 1). Its North Pole denotes the octave, the South Pole denotes the tonic and the 36 notes of the six scales other than the D scale are spread along six great circles, the 12 notes of the D and D’ scales being distributed along their common vertical diameter. The numbers of notes of each tone ratio are shown below:

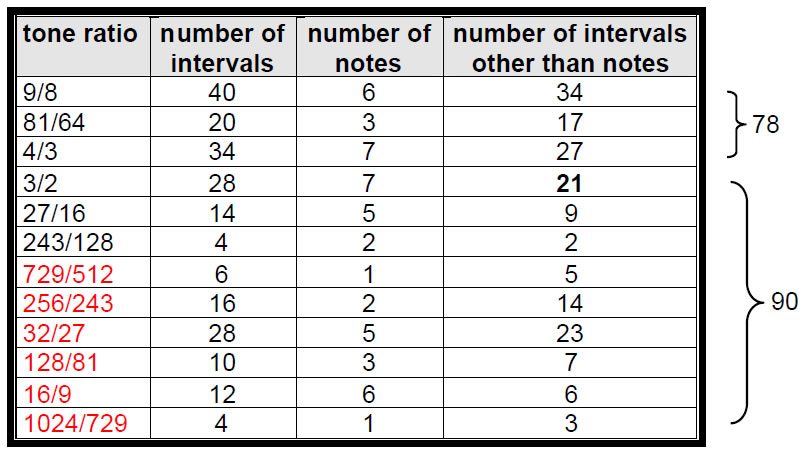
The tone ratio 729/512 appears only once as a note but (according to Table 1) six times as an interval, i.e., five times as an interval between notes above the tonic. Similarly, the tone ratio 1024/729 appears only once as a note but four times as an interval, i.e., three times as an interval between notes above the tonic. Tabulated below for the eight Church musical modes are the numbers of intervals, notes and intervals other than notes, i.e., intervals between notes above the tonic:

3

Table 2. Numbers of intervals other than notes in the eight Church modes.

We see that every different tone ratio appears more than once, i.e., is repeated in the eight D–D′ scales. There are 168 repetitions of these intervals. This is remarkable because 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, which has been shown in previous articles to appear in many different contexts because it is the structural parameter of the heterotic superstring and must therefore characterise all other holistic systems. This is excellent evidence of the holistic nature of the eight Church musical modes. More remarkable still, Table 2 shows that the number value 78 of Cholem is the number of intervals that are seconds, thirds or perfect fourths and the number value 90 of Yesodoth is the number of the nine remaining types of intervals (Fig. 2). Can any other combinations of numbers of intervals have these two

numbers as their sums? The number of repeated, non-Pythagorean intervals is 58, so this does not provide an alternative combination. Arranged in order of the sizes of their intervals, the numbers are:

14   34   23   17   27   3   5   21    7   9   6   2

It is readily confirmed that no sequence of monotonically increasing integers starting from the extreme left or right adds up to 78 or 90. Combinations of integers adding to these numbers do exist, but they are non-sequential (e.g., 14 + 34 + 27 + 3 = 78), which reduces their plausibility as alternatives. The second, third and fourth notes of the Pythagorean musical scale are sequential, not randomly placed, and it is the natural manner in which the number 78 appears that makes mathematical design, rather than random chance, the reason why it does so. Why should the superstring structural

4

parameter 168 appear here at all if all the connections with the Kabbalistic number values previously referred to are merely coincidental, instead of indicating the fact that the Tree of Life is the universal design of all holistic systems?

We found earlier that the 204 repetitions of the 12 basic types of intervals between notes of the eight D–D’ scales comprise 134 Pythagorean intervals and 70 non-Pythagorean intervals. The two D scales have eight Pythagorean notes and four non- Pythagorean notes arranged on the central axis of the sphere shown in Fig. 1. (134–8=126) Pythagorean intervals are therefore not notes of the D scales. Including the tonic and octave, there are 10 Pythagorean notes arranged along the central axis, 70 non-Pythagorean intervals and 126 Pythagorean intervals, that is, 206 intervals, where

206 = 126 + 10 + 70,

126 = 37(9/8) + 19(81/64) + 31(4/3) + 25(3/2) + 11(27/16) + 3(243/128),

10 = 1 + 2(9/8) + 2(4/3) + 2(3/2) + 2(27/16) + 2,

and

70 = 5(729/512) + 15(256/243) + 27(32/27) + 9(128/81) + 11(16/9) + 3(1024/729).

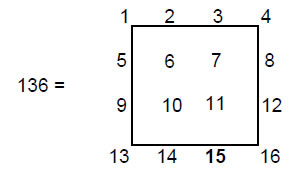
The 206 intervals comprise the tonic, octave, and 204 repetitions of the 12 basic types of notes making up the seven scales. They consist of 136 Pythagorean intervals and 70 non-Pythagorean intervals.

The Tetrad Principle⁴ determines the 136 Pythagorean intervals because 136 is the sum of a 4×4 square array of the first 16 integers:

The principle determines the 70 non-Pythagorean intervals because the number 70 is the fourth of the 4-dimensional, tetrahedral numbers beyond 1.*

It was shown in Article 29⁵ that the simplest Catalan solid — the triakis tetrahedron — is built from 137 vertices, edges and triangles, thus embodying the number that defines the fine structure constant e²/ħc ≈ 1/137 well-known to physicists as determining the strength of the coupling of an electromagnetic field to electrically charged particles. 136 geometrical elements therefore surround the centre of the triakis tetrahedron. Article 30⁶ proved that this polyhedron is a holistic object in the sense that it is geometrically equivalent to the outer form of the Tree of Life and to the Lambda tetractys — the tetractys form of the pattern of integers shaped like the Greek letter lambda that was the mathematical basis of Plato’s account in his book Timaeus of the dividing out of the celestial spheres by the Demiurge. The fact that there are as many Pythagorean intervals in the eight Church musical modes other than their basic notes as there are geometrical elements in this polyhedron indicates that the complete set

_______________________________________

* A tetrahedral number is that generated by counting dots arranged as triangular arrays in sheets, starting with one at its apex and with each successive sheet adding one more dot along each side of its array. A 4-dimensional, tetrahedral number is that generated by piling tetrahedra representing successive tetrahedral numbers into a 4-dimensional tetrahedron.

5

of musical scales is, too, a holistic system.

126 is the sum of the number values of the four types of combinations of the letters A, H and I in EHYEH (AHIH), the Godname of Kether:

A = 1, H = 5, I = 10

1	A + H + I	=   16
2	AH + HI + AI + HH	=   42
3	AHI + HIH + AHH	=   47
4	AHIH	=   21
	Total	= 126

 

 

 

 

 

The number 126 has the remarkable property that it is the arithmetic mean of the first 26 triangular numbers, where 26 is the number value of the Godname YAHWEH:

These properties show how EHYEH and YAHWEH prescribe the number of repeated Pythagorean intervals between the notes of the eight Church musical modes.

As the axis of the triakis tetrahedron is made up of two edges and three vertices of triangles, that is, five geometrical elements, (137–5=132) geometrical elements surround this axis. Of these, six are its vertices, leaving (132–6=126) geometrical elements that are not vertices of the

polyhedron. This is how EHYEH (“I am”) prescribes the number of extra geometrical elements needed to build the triakis tetrahedron, starting from its eight vertices and its central axis. The 126 elements correspond to the

6

126 repetitions of the Pythagorean intervals of the eight Church modes, whilst the eight vertices of the triakis tetrahedron correspond to the eight Pythagorean notes in the Dorian and Hypomixolydian modes that lie on the axis of the spherical distribution of their 50 notes (see Fig. 1). The triakis tetrahedron is the polyhedral counterpart of this representation of the Pythagorean interval composition of the Church modes.

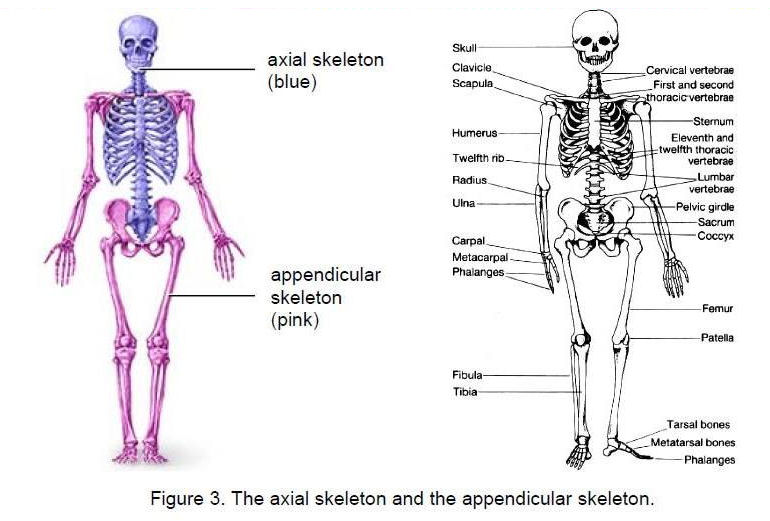
2. The human skeleton
The adult human skeleton usually consists of 206 named bones. Babies are born with 270 soft bones — 64 more than an adult. These will fuse together by the age of 20 or 25 into the 206 hard, permanent bones. They can be grouped in two divisions: the axial skeleton and the appendicular skeleton (Fig. 3). The 80 bones of the axial skeleton form the vertical axis of the body. They include the bones of the head, vertebral column, ribs and breastbone or sternum. The appendicular skeleton consists of 126 bones and includes the free appendages and their attachments to the axial skeleton. The free appendages are the upper and lower extremities, or limbs, and their attachments, which are called girdles. The named bones of the body are listed below by category (numbers in brackets are the numbers of each type):

Axial Skeleton (80 bones)

Skull (28)

Cranial Bones (8)

• Parietal (2)
• Temporal (2)
• Frontal (1)
• Occipital (1)
• Ethmoid (1)
• Sphenoid (1)

Facial Bones (14)

• Maxilla (2)
• Zygomatic (2)
• Mandible (1)
• Nasal (2)
• Platine (2)
• Inferior nasal concha (2)
• Lacrimal (2)
• Vomer (1)

Auditory Ossicles (6)

• Malleus (2)
• Incus (2)
• Stapes (2)

Hyoid (1)
Vertebral Column (26)

• Cervical vertebrae (7)
• Thoracic vertebrae (12)
• Lumbar vertebrae (5)
• Sacrum (1)
• Coccyx (1)

Thoracic Cage (25)

• Sternum (1)
• Ribs (24)

Appendicular Skeleton (126 bones)

Pectoral girdles (4)

• Clavicle (2)

7

• Scapula (2)

Upper Extremity (60)

• Humerus (2)
• Radius (2)
• Ulna (2)
• Carpals (16)
• Metacarpals (10)
• Phalanges (28)

Pelvic Girdle (2)

• Coxal, innominate, or hip bones (2)

Lower Extremity (60)

• Femur (2)
• Tibia (2)
• Fibula (2)
• Patella (2)
• Tarsals (14)
• Metatarsals (10)
• Phalanges (28)

Comparison with the Church musical modes
Just as there are 206 bones in the adult human body, so there are 206 repeated intervals between the notes of the eight Church modes when they are represented by points on a sphere whose axis contains the two D scales (Dorian and Hypodorian modes). The 126 bones of the appendicular skeleton correspond to the 126 repeated Pythagorean intervals. The 80 bones of the axial skeleton correspond to the 10 Pythagorean notes on the axis of the sphere and to the 70 non-Pythagorean intervals. The number value of Yesod, the penultimate Sephirah of the Tree of Life, is 80. Its meaning of “foundation” aptly applies to the role played by the axial skeleton vis-à-vis the body, for it can be regarded as its essential core.

Comparison with polyhedra
Kabbalistically speaking, the skeleton is the most ‘Malkuth’ aspect of the body. The Godname ADONAI assigned to Malkuth has the number value 65. Table 1 in Article

8

30⁷ indicates that this is the number of vertices, edges and triangles making up the triakis tetrahedron when its faces and internal triangles are each considered as single triangles (this was called ‘case D’ in previous articles). ADONAI (“Lord”) prescribes the Catalan solid whose 126 geometrical elements other than vertices surrounding its axis correspond to the 126 bones of the human appendicular skeleton.

Comparison with the Tree of Life
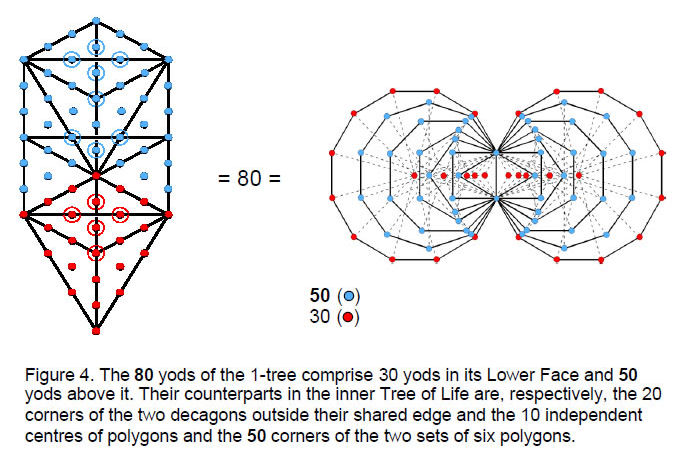
Conversion of the 19 triangles of the lowest (the so-called ‘1-tree’) of any set of overlapping Trees of Life generates 80 yods (Fig. 4). 30 yods belong to what Kabbalists call the ‘Lower Face’ (the kite-shaped section spanned by Tiphareth, Netzach, Hod, Yesod & Malkuth) and 50 yods belong to the remainder of the Tree of Life. In general, the number of yods in the lowest n Trees of Life is

Y(n) = 50n + 30.

(Note that Y(1) = 80). The Tree of Life has 70 yods, so that 10 yods are added by its conversion into the 1-tree. The inner form of the Tree of Life consists of two similar sets of seven enfolded, regular polygons that share an edge joining Tiphareth to Daath. They are the triangle, square, pentagon, hexagon, octagon, decagon and dodecagon. They have 70 corners, their 94 sectors having 80 corners. The 70 corners of the 14 polygons and their 10 centres that are not also corners of polygons are the counterpart of the 70 yods of the Tree of Life and the extra 10 yods of

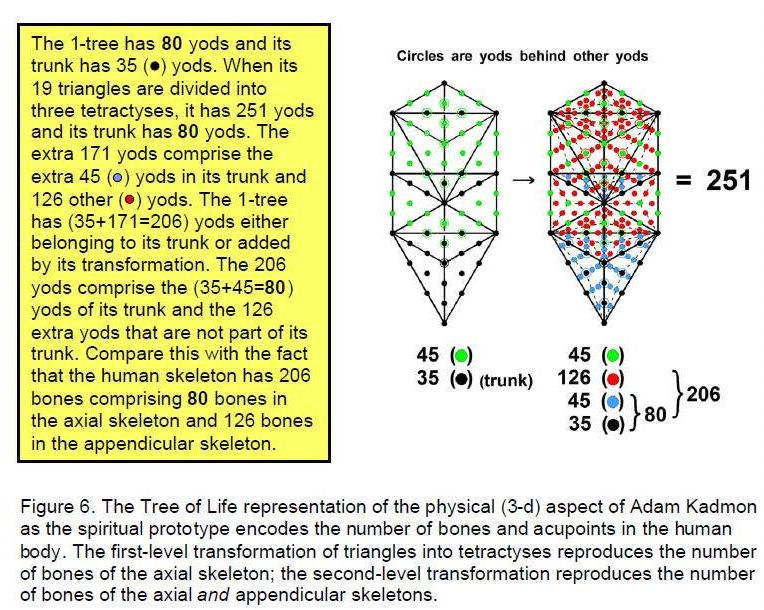
                                                                                      Figure 5. The 80 yods of the trunk of the 1-tree denote the 80 bones of the axial skeleton.
                                                                                      The 126 yods outside the trunk denote the 126 bones of the appendicular skeleton.

the 1-tree.

The ‘trunk’ of the Tree of Life consists of the vertical sequence of a point, line, triangle and tetrahedron whose vertices symbolize the integers 1, 2, 3 & 4 (Fig. 5). The point is located at Kether, the line is the path joining Chokmah and Binah, the triangle is that with Chesed, Geburah and Tiphareth at its corners and the tetrahedron has Netzach, Hod, Yesod and Malkuth at its vertices. The trunk contains 35 yods, the remainder of the Tree of Life (its ‘branches’) comprising 35 yods as well. Their counterpart in its

9

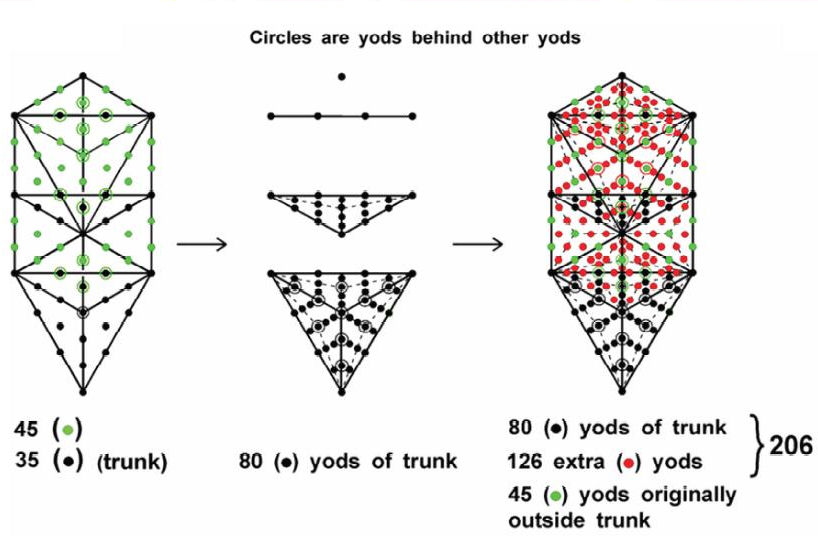
inner form is the 35 corners associated with each set of polygons. Suppose, now, that the 19 triangles making up the 1-tree are each divided into three triangles, which are then turned into tetractyses. Nine yods are added to each of the five triangles of the trunk, i.e., 45 yods in total. Instead of having 35 yods, the trunk now has (35+45=80) yods. The 14 triangles with 45 yods forming the branches of the 1-tree have (14×9=126) yods added to them, so that they now contain (45+126=171) yods. The 1-tree has 80 yods in its trunk and 171 yods in its branches — 251 yods in all. The meaning of this number in the context of the heterotic superstring interpretation of the basic unit of matter described by Annie Besant and C.W. Leadbeater⁸ has been discussed in previous articles⁹ by the author. Its significance for the human body will be made clear later. What needs to be pointed out here is the remarkable fact that, just as the axial skeleton has 80 bones and the appendicular skeleton has 126 bones, so the trunk of the Tree of Life has 80 yods and its branches have 126 yods added by the conversion of its triangles into three tetractyses.

It seems natural to identify the axial skeleton with the trunk of the Tree of Life because they play the same role. The former is the essential, coordinating core of the skeleton and the latter represents the four-stage sequence in the generation from a mathematical point of the simplest regular polyhedron — the building block of solid geometry. Fig. 6 shows how the 206 bones of the human body are denoted by the 206 yods that either belong to the trunk of the 1-tree or are added by the second-level transformation of its triangles. Truly, the human body is designed “in the image of God” as written in Genesis 2:27. That image is Adam Kadmon.

The following consideration provides evidence that this correlation between the bone

10

composition of the human body and the yod make-up of the Tree of Life is not a coincidence. The Godname ADONAI assigned to Malkuth has a number value of 65. This is the number of Sephirothic emanations in the 10-tree. ADONAI MELEKH, its complete Godname, has the number value of 155, which is the number of emanations in the 25-tree. The complete and partial Divine Names thus define, respectively, 25 and 10 Trees of Life. Compare this with the prediction by string theory that space has 25 dimensions and with the prediction by M-theory that it has 10 dimensions. They can be made consistent with each other by supposing that M-theory is not fundamental, as currently supposed, but is derived from a theory in 26-dimensional space-time. The implication of this is that dimensions of space can be modelled as Trees of Life. The three lowest trees of the 25 overlapping Trees of Life would then represent the 3-dimensional space of the macroscopic universe and the 22 higher trees would represent the remaining 22 compactified dimensions.

The inner form of the Tree of Life has 70 polygonal corners, two of which (the topmost corners of the two hexagons) coincide with the lowest corners of the pair of hexagons enfolded in the next higher, overlapping Tree of Life. There are 68 corners intrinsic to the two sets of polygons enfolded in each Tree of Life. The number of corners of the 14n polygons enfolded in n overlapping Trees of Life is given by

C(n) = 68n + 2,

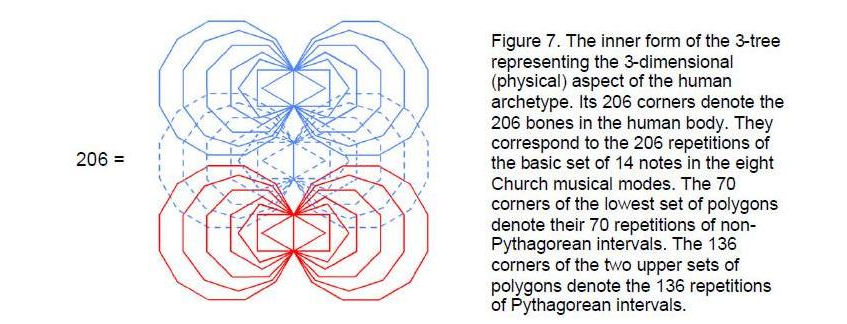
where the number ‘2’ denotes the uppermost corners of the two hexagons enfolded in the nth tree. As the manifestation of the Tree of Life blueprint in macroscopic space, the human body would be made up of basic structural units whose number was equal to the number of geometrical

degrees of freedom of the inner form of the 3-tree represented by the corners of the 42 polygons enfolded in it, i.e., C(3) = 206 (Fig. 7). This is the number of bones in the adult human body!

11

As confirmation that this result cannot be coincidental as well, remember that it was found earlier that the 206 repetitions of the basic set of 14 notes in the eight Church musical modes represented by a sphere consist of 70 non-Pythagorean intervals and 136 Pythagorean intervals. The former correspond to the 70 corners of the lowest set of polygons and the latter correspond to the 136 corners of the two upper sets of polygons. Indeed, the two corners of the uppermost pair of hexagons denote the tonic and the octave.

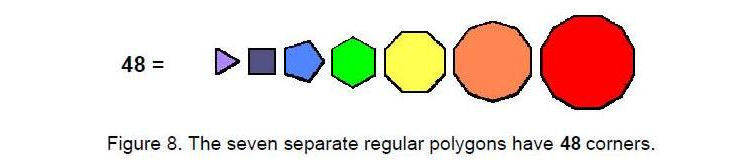
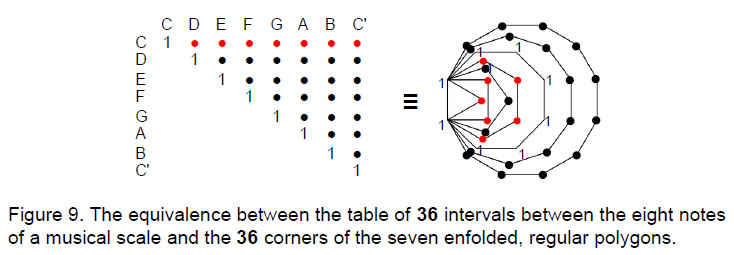
The 48 corners of the seven separate regular polygons making up the inner form of the Tree of Life denote the 48 notes between the tonic and octave of the eight Church modes (Fig. 8) whilst the 36 corners of the seven enfolded polygons (Fig. 9) denotes the 36 intervals of each mode, namely, the eight intervals between a note and itself (the ‘1’s in Fig. 9) and the 28 intervals between different notes. As the ancient Pythagoreans taught, music is geometry. Similarly, the bone structure of the human body reflects the sacred geometry of the blueprint for Adam Kadmon.

Let us write the sets of bones in the axial and appendicular skeletons as:

206 = 80 + 126,

where

80 = 28 + 1 + 26 + 25

and

126 = 4 + 60 + 2 + 60,

the underlining indicating that sets of bones, rather than simple numbers, are being considered here. Having found that: 1. the number of bones in the adult human body is the number of repetitions of the basic set of 12 notes between the tonic and octave of the eight Church modes, and 2. the modes contain 168 intervals other than notes, it is interesting to raise the question of whether 168 bones can be identified in a natural way as corresponding to these intervals. According to Table 2, the 168 intervals comprise 110 Pythagorean intervals and 58 non-Pythagorean intervals. The 206 intervals comprise 136 Pythagorean intervals and 70 non-Pythagorean intervals. Therefore, the 168 intervals have 26 fewer Pythagorean intervals and 12 fewer non-Pythagorean intervals. There appears to be no skeletal counterpart to the distinction between Pythagorean and non-Pythagorean tone intervals. However, we found earlier that the 80 intervals corresponding to the 80 bones of the axial skeleton comprise 10 Pythagorean intervals and 70 non-Pythagorean intervals, whilst the 126 intervals corresponding to the 126 bones of the appendicular skeleton are all Pythagorean. Hence, the 12 fewer non-Pythagorean intervals have to come from the 70 non-

12

Pythagorean intervals within the set of 80. As 80 contains the 26, it is natural to identify the 26 bones of the vertebral column with the 26 Pythagorean intervals that have to be subtracted from the set 206. This leaves 12 bones to be identified in the sets 28, 1, and 25. The 28 bones in the skull consist of eight cranial bones, 14 facial bones and six ossicles. The 25 bones of the thoracic cage consist of 24 ribs and one sternum. These classes do not permit a natural selection of 12 from complete classes and so the identification of the 26 with the 26 Pythagorean intervals is wrong. Instead, the latter must be identified with the 1 and 25, so that the 12 bones come from the sets 28 and 26. The latter comprises seven cervical vertebrae, 12 thoracic vertebrae, five lumbar vertebrae, one sacrum and one coccyx. There are four possibilities for the 12 bones:

A. 12 thoracic vertebrae;
B. six ossicles, five lumbar vertebrae and one sacrum;
C. six ossicles, five lumbar vertebrae and one coccyx;
D. seven cervical vertebrae and five lumbar vertebrae.

Because of the holistic character of the number 168 established in many earlier articles, it seems counter-intuitive to consider the 168 bones as made up of only some, not all, of the facial bones. This leaves only possibilities A and D. The former is the stronger one because it is more natural, not mixing different classes of bones, although one would like a stronger reason than this in order to give more certainty to its choice. Given this qualification, the 168 bones are:

168 = 28 bones of skull + 7 cervical vertebrae + 5 lumbar vertebrae + 1 sacrum + 1 coccyx + appendicular skeleton.

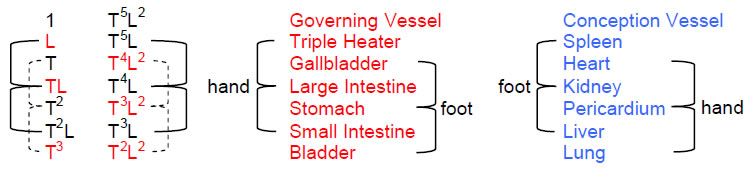
They comprise 42 bones of the axial skeleton and 126 bones of the appendicular skeleton. Both numbers are prescribed by the Godname EHYEH assigned to Kether with number value 21 because 42 is the 21st even integer and, as we saw earlier, 126 is the sum of the number values of the four types of combinations of the letters A, H and I in EHYEH (AHIH). This Godname prescribes the number 168 also because, if the number 21 is assigned to each of the 80 yods of the 1-tree, their sum is 1680, which has been discussed in many previous articles as the structural parameter of the E₈×E₈ heterotic superstring.

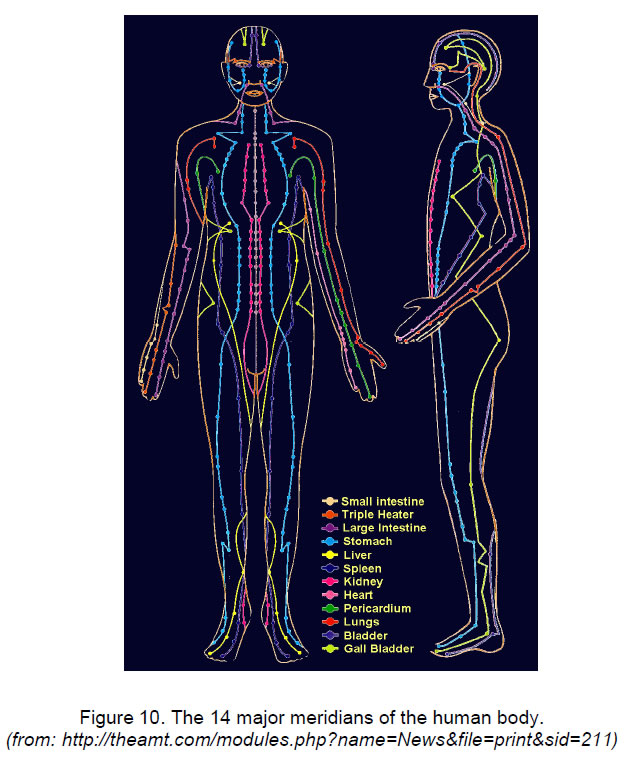
3. Acupuncture
Acupuncture is a complex branch of ancient Chinese medicine that is based on principles developed in China over the past 2000 years. The foundation in which these principles are set is that there is a subtle life energy, called qi (pronounced chee), circulating though all parts of the body via energy channels, called ‘meridians.’ These meridians connect our head, torso, arms, hands, legs, feet, and all internal organs. According to Chinese medical theory, pain and illness results when the smooth, cyclical flow of qi in the meridians becomes blocked or unbalanced. An acupuncturist uses acupuncture needles to stimulate specific points along the meridians. This stimulation helps restore balance and the smooth flow of qi so all parts of the body can work together in harmony as intended. This harmony allows the body to repair itself and maintain health.

The qi energy flows through the meridians in the body in a manner similar to, but not identical to the nervous system or circulatory system. It has been this difference, plus the inability of physics to identify the nature of chi, that has stopped medical acceptance of acupuncture in the West. The presence of qi is important in the organs and bodily systems that require large amounts of energy. However, to the Chinese, qi not only powers a function, but it is inseparable from function, so there can be no

13

 

function without qi and no qi without function. qi is also known as the life force, or the vital force, because the total absence of qi is death. Therefore, the importance of the presence of qi is obvious, but just as important is the proper flow and distribution of qi throughout the meridians in the body. When qi flows smoothly and harmoniously throughout the meridians, every organ and bodily system are in harmony and there is health, but when qi is blocked or unbalanced there is pain and illness. Over 2000 years ago, Chinese physicians discovered that qi circulates  throughout  the  body along fourteen  major channels. Today, these channels are commonly referred to as "meridians." They make up an intricate and invisible network transporting and directing qi to every part of the body. Over centuries
 

As yet, there is no explanation of acupuncture that is compatible with ideas of Western science and medicine. Recently, however, a British scientist, Dr Mae Won Ho, Reader in Biology at the Open University, has proposed that the needles used by acupuncturists may create tiny bioelectrical disturbances. Normally, the water molecules surrounding collagen proteins in the skin and muscle perpetually bond and unbond with other water molecules through the electrical attraction between the two positively charged protons of their hydrogen atoms and the pair of electrons in the oxygen atom of another molecule that is unshared with their hydrogen atoms. When, however, they come into contact with a substance like collagen, the water molecules stop their perpetual sticking and unsticking to one another and arrange themselves in an orderly fashion on the surface of the fibre like scaffolding next to the side of a building. This coating, three or four molecules thick, of ‘ordered water’ improves the electrical conductivity of collagen. Dr Ho proposed in The American Journal of Alternative Medicine that acupuncturists may be transmitting electrical signals from one part of the body to another through the coats of water molecules surrounding collagen fibres. She thinks that these water channels correspond to the meridians. As electric current flows along paths offering the least electrical resistance, this would explain why organs in the path of a meridian could be electrically stimulated at a site in the body on that meridian that had no nerves directly connecting one to the other, thus solving one of the problems that acupuncture has always posed for Western medicine. As acupuncture points are sites where the meridians pass close to the surface of the skin, it would also explain why electrical resistance is relatively lower in these areas. Evidence that signals, indeed, do travel along the meridians was provided by Dr. Helene Langevin, a neurologist at the University of Vermont College of Medicine. In a series of studies using ultrasound, Langevin has found evidence that the meridians lie along the sheets of connective tissue that surround organs. By analyzing meridians in the arm of a cadaver, Langevin said she discovered "that 80 percent of the acupuncture points coincided to where the major connective tissue plane was. We also did a statistical analysis -- this was not due to chance."

of trial and error and meticulous observation, the Chinese accurately mapped the locations of the meridians and identified 361 regular acupuncture points on the major meridians where qi can be accessed and stimulated when there is an abnormality of flow. Over time, many more points have been discovered, as well as so-called extra meridians. The smooth and balanced flow of qi can be affected by any noxious substance, both external and internal, including poor nutrition, impure food, toxic air or water, infectious or contagious diseases, malfunction of an organ, and traumatic or overuse injuries Excessive dampness, wind, cold, heat, and emotional responses to life such as worry, anxiety, stress may affect the flow of qi through the meridians.

In order to properly reach and serve all parts of the body, qi needs to flow smoothly and freely throughout the meridian network. This free flow also allows for all the body organs and systems to communicate and function harmoniously. That leads to sound health. However, any sustained blockage or other disruption of a smooth, balanced flow of qi may lead to pain, ill health, or a weakened immune system. It is necessary to realize that a blockage not only causes diminished qi in one organ or part, but it may also cause excessive build-up of qi in another area. This phenomenon can be understood by visualizing a meridian carrying qi as like water flowing down a river. If a dam is constructed on a river, there is not only less water down the river, but there is a pooling of water up the river. A blockage may cause a deficiency of qi beyond the

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

14

blockage and a build-up of qi before the blockage, which may mean diminished activity of some organs and accelerated activity of others. Either way, if there is a blockage then qi is unbalanced, so its flow must be normalized for health to return. Treatment therefore involves using needles to stimulate the right acupuncture points in order to unblock qi and achiever balance within the meridians.

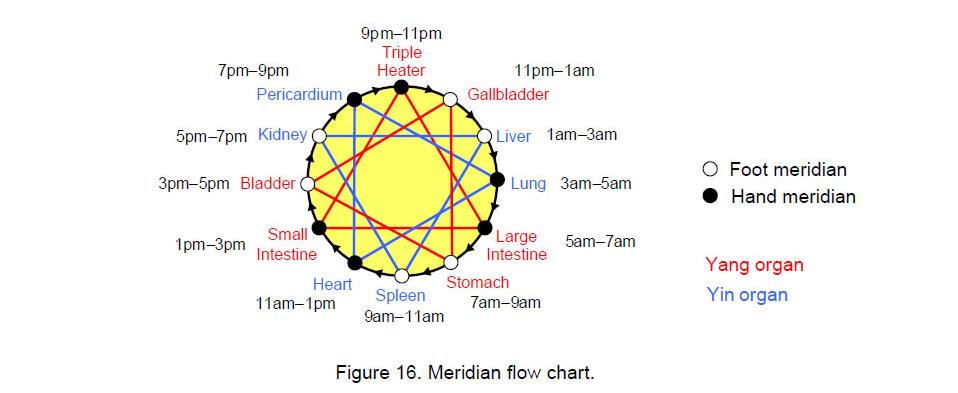
There are 14 major meridians. One, the Governing Vessel, passes along the spine and another, the Conception Vessel, passes along the midline of the abdomen. The twelve regular meridians consist of six Yang channels and six Yin channels (Fig 10) that start at points on the fingers and toes of the extremities. There are three Yang channels and three Yin channels on each side of the body. There are numerous minor ones, which form a network of energy channels throughout the body. Each meridian is related to, and named after, an organ or function. The main ones are: the lung, kidney, liver, stomach, spleen, heart, small intestine, large intestine, gall bladder, urinary bladder, triple heater and pericardium (heart protector/or circulation sex meridian). There are also eight ‘extraordinary vessels’ or channels in acupuncture that are considered to be

15

reservoirs supplying qi and blood to the twelve regular channels, as well as receptacles for excess qi and blood. These are believed to have a strong connection to the kidney. As well as these, there are ‘collaterals,’ smaller, thinner branches of the meridians that run horizontally and obliquely across the body.

The acupoints are of three types:

1. meridian points. These are located along each meridian and arranged symmetrically on both sides of the body except the ones along its midline;
2. extra points. Discovered much later than those found by the ancient Chinese practitioners of acupuncture, they supplement the meridian points;
3. ah-shi points. These are not on the meridians and are not extra points. They are sensitive areas.

The ancient Chinese people discovered 361 acupoints in human beings, 173 acupoints in horses and 70 acupoints in dogs. The points that were discovered in ancient times are called "Classical Points.” Their numbers in each meridian for humans are listed below:

Lung Meridian	11
Large Intestine Meridian	20
Stomach Meridian	45
Spleen Meridian	21
Heart Meridian	9
Small Intestine Meridian	19
Bladder Meridian	67	Total number of acupoints = 361.
Kidney Meridian	27
Pericardium Meridian	9
Triple Heater Meridian	23
Gall Bladder Meridian	44
Liver Meridian	14
Governing Vessel	28
Conception Vessel	24

Hundred of more points have been discovered over the years. However, the classical points remain the primary ones commonly used by acupuncturists.

4. The Tree of Life basis of acupuncture points
We found earlier that the number of bones in the human body is the number of corners of the 42 polygons enfolded in the 3-tree, that is, its inner form. We will now show that the number of acupoints in the human body is embodied in the outer form of the 3-tree.

The n-tree consists of (6n+5) vertices (Sephirothic emanations), (16n+9) edges (Paths) and (12n+7) triangles. The total number of geometrical elements is (34n+21). There are 55 geometrical elements in the 1-tree, where

This demonstrates the beautiful, Pythagorean properties of the 1-tree, the 80 yods of whose 19 tetractys-transformed triangles correspond to the 80 corners of the 94 sectors of the 14 enfolded regular polygons that constitute the inner form of the 1-tree. The number 19 is the tenth odd integer, showing again how the Pythagorean Decad

16

determines the number of triangles making up the 1-tree. The Godname Elohim assigned to Binah with number value 50 prescribes its form because there are 50 hexagonal yods on the 25 edges of the triangles. The number of yods on the edges of these triangles is 61, which is the 31st odd integer. This shows how the Godname EL assigned to Chesed with number value 31 prescribes the shape of the 1-tree.

Suppose that each triangle in the n-tree is divided into three triangles. This adds (12n+7) vertices and 3(12n+7) edges and creates 3(12n+7) triangles. The geometrical composition of the n-tree is:

number of vertices: 6n + 5 + 12n + 7 = 18n + 12;
number of edges: 16n + 9 + 3(12n+7) = 52n + 30;
number of triangles: 3(12n+7) = 36n + 21;

Total number of geometrical elements = 107n + 64.

The 1-tree now has 57 triangles with 30 vertices and 82 edges, that is, 169 geometrical elements. Starting from its top, 168 geometrical elements are needed to construct the 1-tree, demonstrating par excellence the structural character of the number 168 as the number value of the Mundane Chakra of Malkuth. No wonder, therefore, that it should be the superstring structural parameter, as discussed in many previous articles! It is made up of 87 vertices and triangles. The number value of Levanah, the Mundane Chakra of Yesod, prescribes the geometry of the 1-tree, too!

Suppose next that the triangles of the n-tree are transformed into tetractyses. The yod composition of the n-tree is:

Number of yods at corners = 18n.
Number of hexagonal yods on edges = 2(52n+30) = 104n + 60.
Number of hexagonal yods at centres of tetractyses = 36n + 21.
Total number of hexagonal yods = 140n + 81.
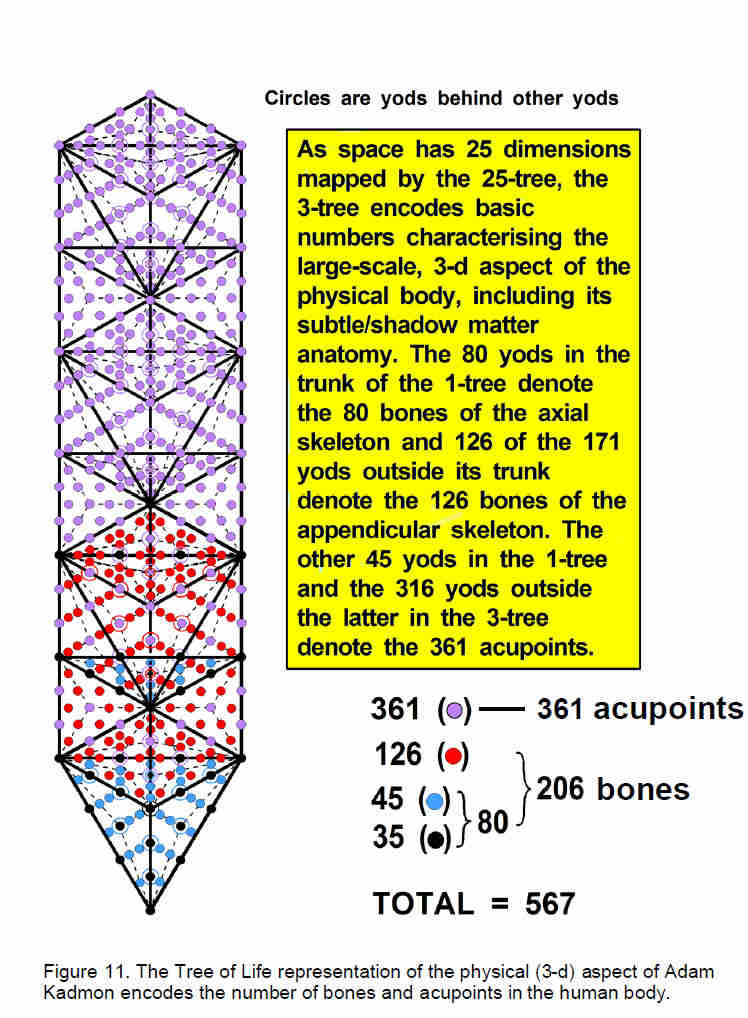
Total number of yods = 18n + 12 + 140n + 81 = 158n + 93.

The 1-tree has 251 yods — 171 more yods than the original 1-tree. The trunk of the 1-tree, which originally comprised 35 yods, is now made up of 80 yods (the same as the original 1-tree) because each of its five triangles adds 9 yods when it is divided into three tetractyses. This means that the branches of the 1-tree, which originally contained 45 yods, now contain 171 yods. The 126 yods added to the branches denote the 126 bones of the appendicular skeleton, whilst the 80 yods of the trunk of the 1-tree denote the 80 bones of the axial skeleton. The 1-tree contains 206 yods denoting the 206 bones of the human skeleton and 45 yods that were the branches of the original 1-tree.

What do these remaining 45 yods signify? Indeed, what is the physical meaning of the branches of the 1-tree vis-à-vis the human body? We found earlier that the inner form of the 3-tree has 206 corners symbolizing the 206 bones of the human body. So let us consider the outer form of the 3-tree. According to the formulae listed above, the 3-tree has 66 vertices and 186 edges of 129 triangles. It also has four tetrahedra, totalling 385 geometrical elements, where

This beautifully demonstrates how the Decad expresses the geometrical make-up of the 3-tree that maps the 3-dimensional human body. We saw earlier how it defines the 55

17

vertices, edges and triangles in the 1-tree. The number of vertices, edges and triangles in the trunk of the 1-tree when its triangles are turned into three tetractyses is also 55! The number of yods in the 3-tree is 158×3 + 93 = 567. The 3-tree has 251 yods in the 1-tree and (567–251=316) yods above the latter. Including the 45 yods outside its trunk, there are (316+45=361) yods in the 3-tree outside the trunk of the lowest tree. These denote the 361 classical acupoints of the human anatomy (Fig. 11). Other points found by many generations of acupuncturists might correspond to the additional yods

18

generated by dividing each of the 129 triangles in the 3-tree into three triangles.

The trunk of the 1-tree initially had five triangles that became 15 triangles. The number value 15 of the Godname YAH defines the part of the 1-tree that manifests in the human body as its axial skeleton. As we have seen, the Godname EL of Chesed prescribes the 1-tree. The 3-tree has 129 triangles. 129 is the number value of YAHWEH SABAOTH, Godname of Netzach. As the 1-tree has 57 triangles, there are (57–15=42) triangles forming the branches of the 1-tree and (129–15=114) triangles forming the branches of the 3-tree, that is, 72 more triangles. 72 is the number value of Chesed. The 3-tree has 66 vertices, where 66 is the 65th integer after 1. This shows how ADONAI, the Godname of Malkuth with number value 65, prescribes the Tree of Life representation of the human skeleton with 206 bones and the system of 361 acupoints.

The list given earlier shows that the stomach meridian (the blue channel in Fig. 10) has 45 acupoints. Can they be identified with the 45 yods of the branches of the original 1-tree? No, because these yods are spread over seven major columns, whereas a meridian corresponds to one or two columns. The agreement of these numbers is only a coincidence. How, precisely, the yods in the columns are correlated with the populations of acupoints in meridians must await analysis in a future article. The 14 meridians consist of 12 principal meridians (six Yang meridians and six Yin meridians), the Governing Vessel, which runs from the base of the spine up the midline of the back and over the head to a spot just above the upper lip, and the Conception Vessel, which runs from the perineum up the midline of the front of the body to the chin. They are two of the eight extra meridians that interlace the 12 principal meridians, helping reinforce the communication between and adjustment of the twelve principal meridians. The eight extra meridians are not directly related to any of the internal organs. There are also twelve divergent meridians, which are extensions of the twelve principal meridians. They usually start from the limbs, run deeper into the body and emerge from the body at the back of the neck. Again, these meridians have counterparts in both the left and right sides of the body. They are divided into Yang and Yin divergent meridians. The Yang divergent meridians start from the six principal Yang meridians, and, after travelling through the body, rejoin the principal meridians. The Yin divergent meridians start from the six Yin principal meridians. However, after travelling through the body, they join the Yang principal meridians with which they are externally and internally related.

If a person stands with their arms above their head, all the Yin meridians flow upwards, while the Yang meridians flow downwards. Yin meridians are on the bottom parts of the forearms and on the back of the legs; Yang meridians are on the top of the forearms and the front of the legs. All the meridians begin or end on the fingertips, toe tips, head, or chest. All Yang meridians begin or end on the head or face, while all Yin meridians begin or end on the chest, with the fingertips and toe tips common to both. The 12 principal meridians consist of the three Yang meridians of the hand, the three Yang meridians of the foot, the three Yin meridians of the hand and the three Yin meridians of the foot. There are three Yang and three Yin meridians on either side of the body. Their acupoint composition is as follows:

The Upper Yin Meridians — Travel from the chest to the tips of the fingers.
The heart meridian (9);
the lung meridian (11);
the pericardium meridian (9) Total = 29.

19

The Upper Yang Meridians — Travel from the tips of the fingers to the head.
The small intestine meridian (19);
the triple heater meridian (23);
the large intestine meridian (20) Total = 62.

The Lower Yin Meridians — Travel from the tips of the toes to the chest.
The spleen meridian (21);
the liver meridian (14);
the kidney meridian (27) Total = 62.

The Lower Yang Meridians — Travel from the head to the tips of the toes.
The stomach meridian (45);
the gall bladder meridian (44);
the bladder meridian (67) Total = 156.

The six Yang meridians comprise 218 classical acupoints and the six Yin meridians comprise 91 acupoints, a total of 309 acupoints. This is remarkable because 309 is the 155th odd integer, where 155 is the number value of ADONAI MELEKH, the complete Godname of Malkuth! Here is a spectacular example of how the Kabbalistic divine names prescribe the physical nature of Adam Kadmon. The Governing Vessel and the Conception Vessel have 52 acupoints, where 52 is the 26th even integer, showing how YAHWEH with number value 26 prescribes this number. The three upper Yang meridians have 62 acupoints, as do the lower Yin meridians. 62 is the 31st even integer, where 31 is the number value of EL, Godname of Chesed.

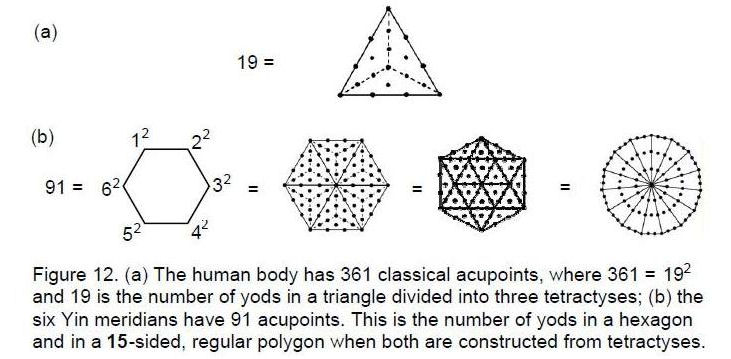
As 361 = 19² and 19 is the 10th odd integer, the Pythagorean Decad symbolized by the tetractys defines the number of acupoints in the human body. Divided into three tetractyses, the triangle contains 19 yods (Fig. 12), showing how the simplest geometrical shape determines the number

of acupoints in the human body. The number of acupoints in the six Yin meridians is 91, where

91 = 1² + 2² + 3² + 4² + 5² + 6².

It is also the number of yods in a six-sided hexagon whose sectors are divided into three tetractyses and in a 15-sided polygon whose sectors are single tetractyses, thus showing how the Divine Name YAH with number value 15 prescribes the number of Yin

20

acupoints. As n² is the sum of the first n odd integers, 91 is the sum of (1+2+3+4+5+6=21) odd integers, showing how the Godname EHYEH with number value 21 prescribes how many acupoints are in the Yin meridians.

The yods of the 3-tree can be viewed as lying on nine vertical lines on each side of the central Pillar of Equilibrium. They are actually arranged in 3-dimensional space and— like acupoints — are connected by crooked, not straight, lines because the Tree of Life is a 3-dimensional object. What is displayed in Fig. 11 is their projection onto the plane passing through the two side pillars of the 3-tree. This may correspond to the intersection of the meridian channels with the surface of the body to create acupoints. On each side of the central Pillar of Equilibrium, there are three major (blue) lines that join yods in the 43 primary triangles of the 3-tree and six minor (red) lines that connect yods in its 129 secondary triangles (Fig. 13). Is it possible that the three major lines on each side of the middle pillar (black line) are the three Yang or Yin meridians and that the six

minor ones pair up to form, respectively, the three Yin or Yang meridians? One must resist the natural temptation presented by Fig. 13 to identify pairs of adjacent red lines sandwiched between blue lines as a meridian. The correct identification may be more complicated. The crucial point is that the Tree of Life mapping of the human body does have columns of yods on each side of its central axis that can be grouped into three of one kind and three of another — in agreement with the existence of three Yang meridians and three Yin meridians on either side of the human body.

Moreover, there are two types of columns of yods on the middle column — those that lie on the Pillar of Equilibrium and those that do not. This suggests a parallel with the acupoints of the

21

Governing and Conception Vessels. The situation may not be quite so simple, however, for there are 10 kinds of yods, each expressing a Sephirah of the Tree of Life. Perhaps only those yods symbolizing a particular Sephirah should be counted as denoting an acupoint of a meridian associated with a particular body organ. Perhaps only yods that follow the sequence of the Lightning Flash down the Tree of Life should be considered. Perhaps even only yods symbolizing the Supernal Triad should be counted on one column as contributing to a particular meridian and only yods symbolizing Sephiroth of Construction should be counted on another column for the same meridian. We also have to take into account the fact that some of the meridians run horizontally, not vertically. This complex issue will be addressed in another article.

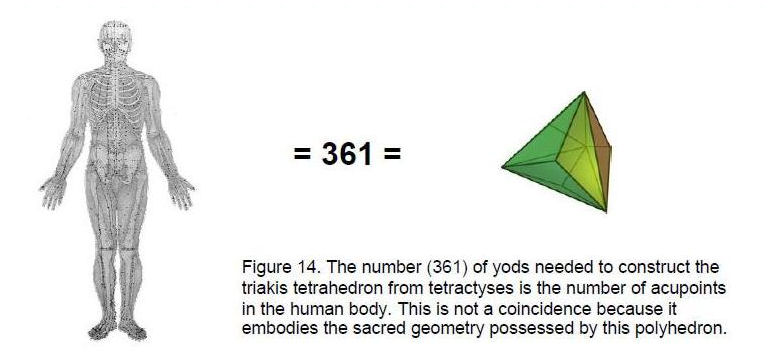
The Catalan solid with the least number of vertices is the triakis tetrahedron with eight vertices, 18 edges and 12 faces. According to Table 3¹⁰ in Article 27, there are 354 yods surrounding the axis of the triakis tetrahedron when its faces and its internal triangles with its centre as a vertex are each divided into three tetractyses. Lying on the axis of the polyhedron formed from the edges of the internal triangles are the central yod and the three yods of the edge on either side of the centre, that is, seven yods. The 90 tetractyses needed to build the triakis tetrahedron therefore have (354+7=361) yods (Fig. 14). This is the number of classical acupoints in the human body. Each yod denotes an acupoint. The simplest Catalan solid embodies not only the number of bones of the appendicular skeleton as the number of geometrical elements other than vertices that surround its axis (see p. 9) but also the number of its acupoints! Although remarkable, this property is not unexpected in view of the fact established in previous articles that the triakis tetrahedron is equivalent to the outer form of the Tree of Life, which is the blueprint for Adam Kadmon, the human prototype. Therefore, these parallels must exist. Moreover, Table 3¹¹ of Article 29 indicates that the triakis tetrahedron is composed of 65 vertices, edges and triangles (internal triangles and their edges included). In other words, the Godname ADONAI directly prescribes its geometrical composition. As ADONAI is the Godname of Malkuth, which is the outer, physical form assumed by the Tree of Life — whatever the scale of space-time this may be on, it indicates the unique relevance of this polyhedral counterpart of the Tree of Life in defining properties of its physical manifestation.

5. The 14 basic, musical notes and the 14 acupuncture meridians
Why does a correlation exist between the interval composition of the Church musical modes and the bones of the human body? Because both the eight D–D’ scales and the physical form of ‘Heavenly Man’ conform to the same universal blueprint called the ‘Tree of Life.’ As further evidence for this profound conclusion, let us compare the 14 basic notes of these scales with the 14 meridians.

Notes

1   256/243     9/8   32/27    81/64   4/3    1024/729     729/512     3/2   128/81    27/16   16/9     243/128 2

There are six pairs of notes, one with tone ratio n and its complement with tone ratio 2/n that is its mirror image in the sequence above:

22

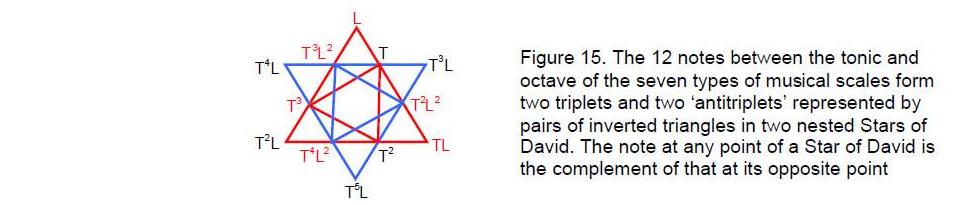
The 12 notes between the tonic and octave form two triplets (T, T², T³) and (T²L², T³L², T⁴L²), whose tone ratios are in the proportions 1:T:T², and two triplets (L, TL, T²L) and (T³L, T⁴L, T⁵L) whose tone ratios are in the same proportions. There are therefore four triplets with the same proportions of their tone ratios (denoted above by solid and dashed brackets). In each pair, one triplet contains notes that are the complement of their corresponding notes in the other triplet. These double and triple relationships can be represented by two Stars of David (Fig. 15), one nested inside the other. The three points of one red or blue triangle denote a triplet of notes and the three points of the inverted blue or red triangle denote the ‘antitriplet’* of its complementary notes. The tonic and octave may be thought of as the centre of the star nest.

Meridians
In order to understand how the holistic systems of scales and meridians are analogous, it is necessary to discuss the cyclical flow of qi around the latter. Just as the sequence of notes in successive octaves is cyclical, so the ebb and flow of qi in each meridian is periodic, as now described. The circulating pathways of the twelve meridians flow from the face to the feet, from the feet to the chest, from the chest into the hands, and from the hands back to the face. The Yang meridians generally flow along the outward (lateral) side of the limbs and along the back of the body. The Yin meridians pass along the inward (medial) side of the limbs and along the front of the body. The pathways leading to or from the arms are called ‘Hand Meridians,’ and those that descend to the legs or ascend from the legs are the ‘Foot Meridians.’

The three Yin Hand Meridians travel from chest to hand; the three Yang Hand Meridians, from hand to head (face). The three Yang Foot Meridians travel from head to foot; and the three Yin Foot Meridians travel from foot to chest. This describes the circulation of energy over the entire body and delineates the pathways in which qi flows.

With the arms raised over the head palms facing forward, the energy in the three Yin Hand Meridians (Lung, Heart and Pericardium) will be flowing from the chest to the fingertips, upward along the forward portion of the arm. The energy in the three Yang Hand Meridians (Large Intestine, Small Intestine and the Triple Heater) will be flowing from the fingertips, downward on the back part of the arm, to end their flow in the face.

From the head, the energy of two of the three meridians of the Foot (the Bladder and Gall Bladder, but not the Stomach) will be travelling down along the side or back of the body and outward side of the leg to end in the toes. To complete the cycle, the energy in the three Yin meridians of the Foot (Spleen, Liver and Kidney) will be travelling up from the toes along the inward side of the leg, continuing along the front of the abdomen and ending in the chest, at which point the cycle begins again from the chest to the hand. There are exceptions to this, but the general pattern is accurate.

_________________________________________

^*A term borrowed from particle physics. The original theory of quarks was based upon a triplet of so-called ‘up’, ‘down’ & ‘strange’ quarks and a triplet of their antiquark counterparts, or an ‘antitriplet.’

23

The Stomach Channel is one exception. Although it is a Yang meridian, it runs on the front of the body with the Yin meridians, instead of up the back like the rest of the Yang meridians. The other exception is the Governing Vessel, which is a Yang meridian in the centre of the back, in which energy flows upward as opposed to the rest of the major Yang meridians in which energy flows downward.

The Governing Vessel follows the spine upward on the back, travels over the head and ends on the inner surface of the upper lip. It has no direct connections to any internal organ. Its energy flow is Yang and ascends from the bottom of the pathway beginning near the anus. It connects with all the Yang meridians of the body, and is important in many conditions requiring manipulation of the Yang energy of the body.

The Conception Vessel travels up the midline in front of the body. It runs from near the anus to the mouth, and its energy is Yin, ascending from the lower body to the upper, as does the Governing Vessel. In effect, these two meridians vertically encircle the body on its midline, front and back.

These two Vessels are not bilateral. They do not form a direct part of the organ meridian's energy circulation network, nor are they associated with any one organ. They belong to the eight Extra Vessels.

The energy travelling from the chest to the fingertip is predominantly Yin energy. Yet on its way back up the other side of the arm, it becomes Yang energy. The energy changes polarity, from Yin to Yang, or from Yang to Yin, the nearer it approaches the extremities of the limbs.

The energy travelling from the chest to the fingertip begins as predominantly Yin energy, but as the energy approaches the extremity the polarity begins to change, and by the time the tip of the finger is reached the Yin becomes progressively mixed with the Yang energy. Energy travelling from the fingertips to the face begins as mixed Yin/Yang, but, by the time that it arrives in the face, it is predominantly Yang energy.

Energy travelling from the face to the toes begins as predominantly Yang energy. As this Yang energy approaches the lower extremities of the leg, the polarity begins to change again. By the time the toes are reached, the Yang energy is mixed with the Yin energy in almost equal proportions. The return from the toes to the chest causes

24

the transformation again. This Yin energy then flows back into the arm, to continue the cycle.

In the central area of the head and chest, even though the energy passes from one channel to another, there is no polarity change. The head is the area where one Yang meridian joins another Yang meridian, and the chest is where each Yin meridian joins another.

It can be seen, therefore, that as qi circulates through the Primary Meridians, it alternates in coupled pairs of Yin and Yang meridians, staying for two hours in the Yin and two hours in the Yang in a smooth alternating rhythm. Figure 16 charts the flow of qi through the 12 meridians. Although the qi flows constantly around the channels, there is an ebb and flow of the energy in successive meridians every two hours. The flow follows the diurnal cycle of sunlight and darkness. Qi builds up in a given meridian, reaching a maximum then decreasing again to its original level, the process taking two hours. The same cycle then starts up in another meridian. In this way, all 12 major organs of the body receive nourishment of qi over a period of 24 hours. Starting, say, at the Lung Meridian in the arm, qi flows into the Large Intestine Meridian, then into the Stomach Meridian in the leg, followed by the Spleen Meridian also in the leg. Two arm meridians become activated in turn, then two leg meridians, followed by two arm meridians again, and so on. The polarity of the qi switches as it passes from one meridian to another in the same limb, the energy flowing upwards in the Yin meridians and downwards in the Yang meridians. Because of this, each meridian is coupled energetically to one other as follows:

Yin	Yang
Lung	Large Intestine
Spleen	Stomach
Heart	Small Intestine
Kidneys	Bladder
Pericardium	Triple Heater
Liver	Gallbladder

This ebb and flow does not happen in the Governing Vessel and the Conception Vessel. The former is Yang and connects all Yang channels; the latter is Yin and connects all Yin channels.

25

In terms of their starting points or endpoints, the 12 meridians group into four triplets:

1. three Yang Hand Meridians: Large Intestine, Small Intestine, Triple Heater;
2. three Yin Hand Meridians: Lung, Heart, Pericardium;
3. three Yang Foot Meridians: Gallbladder, Stomach, Bladder;
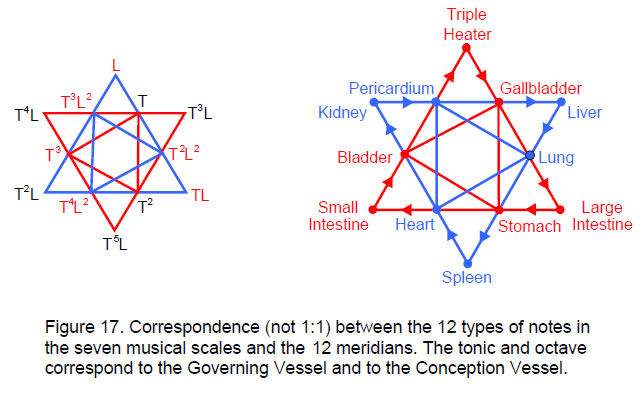
4. three Yin Foot Meridians: Spleen, Kidneys, Liver.

When grouped according to the daily sequence of flow of qi, they form two Stars of David, the ordering of this flow following the edges of the outer Star of David (Fig. 17). This is exactly the same pattern as the six pairs of notes and their complements. The Yin/Yang duality of meridians corresponds to the duality of a musical note and its complement. Just as the alternation of the Yang and Yin phases completes a cycle, so the raising of a note by the interval of its complement and then by its own interval transforms it into the same note of the next higher octave, thus completing a musical cycle, i.e., for a note of tone ratio n: n×(2/n)×n = 2n. The two triplets of notes with tone ratios in the same proportions and the two triplets of their complements correspond to the three hand meridians and the three foot meridians of each polarity:

It should be emphasized that the correspondence shown above should not be read horizontally, i.e., the list of Yang meridians starts with an arbitrary one because, unlike the tones of the scale, no significance can be given to any particular ordering of the meridians. The Triple Heater meridian was placed at the top of the list for convenience of comparison with Fig. 16, in which it was arbitrarily chosen to be at the top of the diagram. The essential features of the analogy are 1. both notes and meridians exist as seven pairs, 2. one of these pairs is distinct from the other six

pairs, 3. the six pairs form four triplets — two pairs of one kind and two pairs that are ‘opposite’ to the first two.

6. Correspondence with the 14 roots of G₂
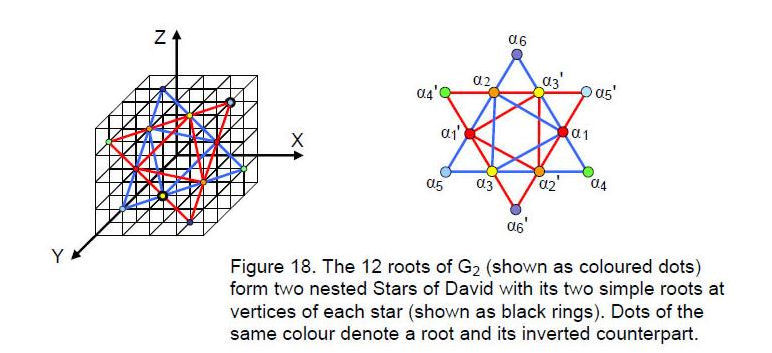
Some physicists are beginning to suspect that G₂, the rank-2, simply connected Lie

26

group, may play a central role in the M-theory that generalizes supergravity and the five superstring theories. This is because it is the group of automorphisms of the octonions, which seem to be the natural basis of the gauge symmetry group E₈ known (together with SO(32)) to describe the unified interactions of superstrings. Its 14 roots consist of a pair of simple roots with rectangular coordinates α₀ = (0, 1, –1) and α₀' = (1, –2, 1) and six pairs of other roots, one member of each pair being the inversion of the other:

α1 = (1, –1, 0) α2 = (–1, 0, 1) α3 = (0, 1, –1) α4 = (2, –1, –1) α5 = (–1, 2, –1) α6 = (–1, –1, 2)

α1' = (–1, 1, 0) α2' = (1, 0, –1) α3' = (0, –1, 1) α4' = (–2, 1, 1) α5' = (1, –2, 1) α6' = (1, 1, –2)

The 14 roots form two Stars of David (Fig. 18). The inner one denotes the first triplet of roots and their inversions. The second triplet and their inversions create the outer one.

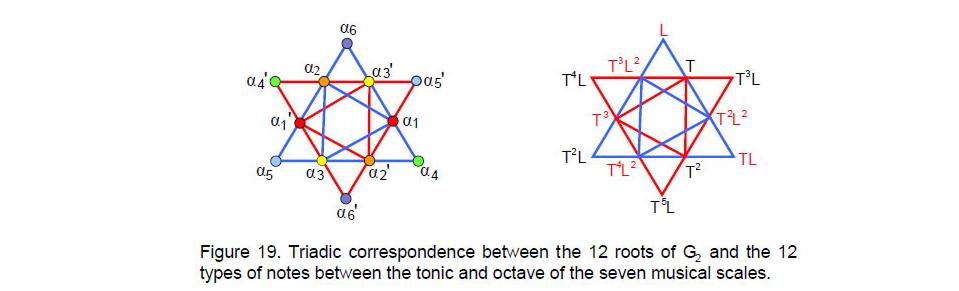
Figure 19 displays the correspondence between the 12 roots of G₂ and the 12 notes belonging to the seven musical scales. The counterpart of a root and its inversion in space (denoted by dots of the same colour) is a musical note of tone ratio n and its complement of tone ratio 2/n. As with the meridians, the correspondence is not to be read horizontally in a 1:1 way between an individual root and a note. What is significant here is that, like the notes and the meridians, there are 12 roots grouped into six pairs and arranged as four triangles in two Stars of David, i.e., their

binary and triadic relationships. The pairing arises from one root being the mirror image of the other. Its counterpart with the pairs of notes is similar because, when all the notes of the scale are arranged in a linear sequence of monotonically increasing tone ratios, a note and its complement are mirror images of each other in this sequence, one note being separated from

27

the tonic by the same interval as its complement is separated from the octave. In the case of the meridians, each pair is of opposite polarity, one meridian being a channel of Yang qi and the other being a channel of Yin qi.

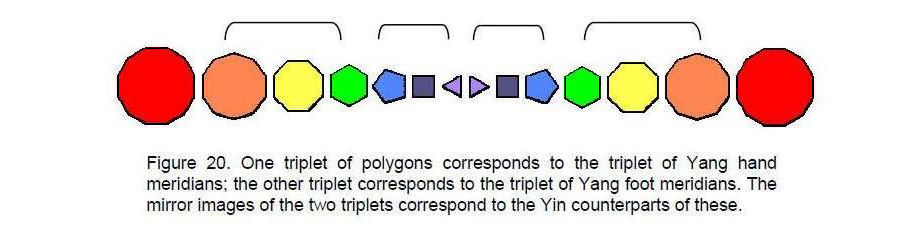
The 14-fold pattern of the notes of the seven different musical scales, the meridians of the human body and the roots of G₂ reflects the similar pattern in the geometry of the inner form of the Tree of Life, which consists of 14 regular polygons. Their arrangement as two sets of seven polygons, one set the mirror image of the other (Fig. 20), corresponds to the seven notes and their seven complements, the seven Yang meridians and the seven Yin meridians and the seven roots of G₂ and their seven mirror images. The first three polygons — the equilateral triangle, square and pentagon — have 3-fold, 4-fold and 5-fold symmetries that are doubled in the second triplet of polygons — the hexagon, octagon and decagon. These two triplets of polygons correspond to the two triplets of notes (L, TL, T²L) & (T, T², T³), to the two triplets of Yang meridians consisting of the three hand meridians and the three foot meridians, and to the two triplets of roots of G₂, (α₁ , α₂ , α₃ ) & (α₄ , α₅ , α₆ ). The mirror images of the two triplets of polygons correspond to the two triplets of complements of the notes (T³L, T⁴L, T⁵L) and (T²L², T³L², T⁴L²), to the two triplets of Yin meridians consisting of the three hand and the three foot meridians, and to the two triplets of roots that are the mirror images of the former set: (α₁', α₂', α₃') & (α₄', α₅', α₆'). The pair of dodecagons correspond to the tonic and octave, to the Governing Vessel and the

Conception Vessel, and to the two simple roots of G₂: α₀ & α₀'.

In the outer form of the Tree of Life, the pattern of two triplets and a singlet is the two triads of Sephiroth of Construction:

Chesed-Geburah-Tiphareth Netzach-Hod-Yesod

and Malkuth (Fig. 21). It is represented in the Pythagorean tetractys as the two triplets of hexagonal yods and the central yod, which symbolize, respectively,

28

 these two triads and Malkuth:

The triplet pattern of the meridians is therefore a reflection of the fact that both the physical body and its subtle matter counterpart of qi and acupoints (the ‘zelim’, as it is called in Kabbalah) are the manifestation of the Tree of Life blueprint in space-time.

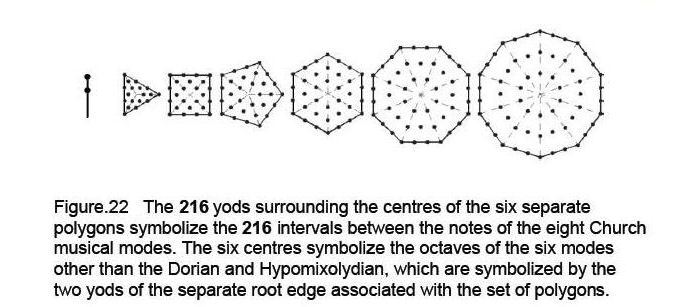
216 yods surround the centres of the first six, separate polygons (Fig. 22). They denote the 216 intervals other than octaves between the notes of the eight Church musical modes. The octaves of the six modes other than the two D scales (the Dorian and Hypomixolydian Modes) are symbolized by the six centres, The two yods of the root edge associated with one set of polygons denote the octaves of the two D scales. One set of polygons embodies 216 rising intervals, the other embodies 216 falling intervals. The Godname ELOHA with number value 36 prescribes

this new holistic subset of polygons because they have 36 corners. Enfolded, they have 26 corners (50 corners for both sets of polygons), showing how the Godnames YAHWEH with number value 26 and ELOHIM with number value 50 prescribe the polygons corresponding to the 12 meridians.

The 48 yods surrounding the centre of the octagon symbolize the 48 notes of the eight Church musical modes between the tonic and octave. The remaining 168 yods symbolize the 168 repetitions of these notes (see p. 4).

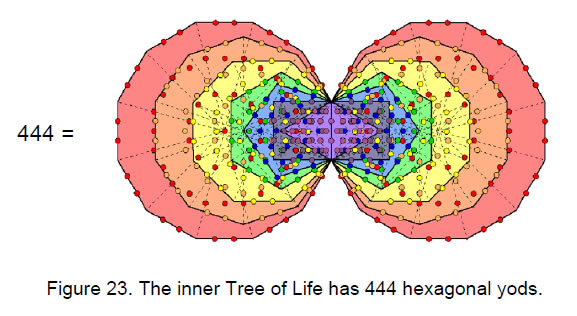
Further proof that the set of six polygons, indeed, do constitute a new Tree of Life pattern is the fact that they are made up of 222 yods, that is, 444 yods for both sets. This is the number of hexagonal yods in the inner Tree of Life (Fig. 23). This is a clear illustration of how the Tetrad (4) expresses mathematical properties of the Tree of Life, whose trunk symbolizes the first four integers. The number of hexagonal yods in the seven enfolded polygons is 224. This is 8×28, that is, the number of intervals between the notes of each musical mode, because each scale has eight notes with 28 intervals.

7. Correspondence with the 14 projective elements of the Fano plane
A projective plane of order n has (1+n+n²) points and (1+n+n²) lines. Each line contains (n+1) points and each point is on (n+1) lines. Because the number of points is the same as the number of lines, the projective plane displays a duality whereby it is unaltered by

29

interchanging lines and points. The simplest projective plane is the Fano plane (n=2). It has seven points and seven lines, i.e., 14 points and lines (Fig. 24). Every point is on three lines and every line joins three points. The seven lines consist of two triplets of lines (the three edges of the triangle and its three medians) and a circle. The seven points consist of two triplets of points at the corners of two triangles and a point at their centre. The Fano plane comprises two triplets of points, two triplets of lines and a point and a circle.

Compare this with the 14 meridians, which are made up of two triplets of Yang meridians, two triplets of Yin meridians and two other meridians — the Governing Vessel, which is Yang, and the Conception Vessel, which is Yin. The following correspondence exists:

Central point		Governing Vessel (Yang)
Circular line		Conception Vessel (Yin)
Triplet of internal points		Three Yang hand meridians
Triplet of external points		Three Yang foot meridians
Triplet of internal lines		Three Yin hand meridians
Triplet of external lines		Three Yin foot meridians

The Fano plane counterpart of Yin/Yang polarities is the duality of lines and points. The choice of associating points with Yang meridians and lines with Yin associations is not arbitrary but predicted on the metaphysical meaning of the masculine generative principle and the feminine, formative or reproductive principle in Nature that, respectively, the Yang and Yin polarities express. A point is shapeless and the precursor of form (the line). Points, therefore, must correspond to Yang meridians and lines must correspond to Yin meridians.

The Fano plane has 168 symmetries described by SL(3,2), the special linear group of 3×3 matrices with unit determinant over the field of complex numbers. Its centre, SZ(3,2) is the set of all scalar matrices with unit determinant and zero trace. SZ(3,2) is isomorphic to the 3rd roots of unity. The three 3rd roots of unity are 1, exp(2πi/3) and exp(4πi/3). Plotted in the Argand diagram (Fig. 25), they are located at the three corners of an equilateral triangle. The cyclic group of order 3 is C₃ = (1, r, r²), where the generator r = exp(2πi/3) is the primitive 3rd root of unity. This reminds us of the four triplets of notes belonging to the seven types of musical scales, whose tone ratios are in the proportion of 1:T:T², where T (=9/8) is the Pythagorean tone interval. In terms of music, the dot at the centre of the Fano plane corresponds to the tonic and the circular line corresponds to the octave, whilst the four triplets of points and lines correspond to the four triplets of intervals and their complements. The musical counterpart of the duality of points and lines in projective space is the way every interval in a scale has its complement. We saw earlier how the same concept arose in the context of the roots of G₂ and their inversions. It also exists in the duality of polyhedra. The 14 notes of the Church modes, the 14 roots of G₂, the 14 meridians, the 14 points and lines of the Fano plane are all manifestations of this universal pattern, embodied geometrically in the inner form of the Tree of Life as its 14 enfolded polygons and in its

 

 

30

outer form as the 14 columns of yods in its tetractys-transformed triangles, namely, two columns (one behind the other) on the central Pillar of Equilibrium, six major columns and six pairs of minor columns (presumably, the counterparts of meridians).

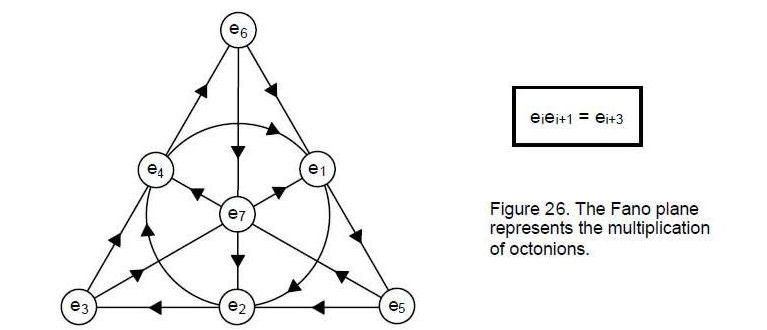
G₂ is the group of automorphisms of the unit imaginary octonions. Their multiplicative algebra is represented by the Fano plane if they are assigned to its points in the way shown in Fig. 26. The multiplication of two octonions is the third on the same straight or curved line provided that their

multiplicative ordering follows the arrow on the line. Their product is minus the third one if multiplication is opposite to the sense of the arrow. The seven lines represent the seven 3-tuples (e_i, e_i+1, e_i+3) (i = 1–7). It was shown in Article 15¹² that there are 84 permutations of pairs and triplets of octonions chosen from the seven 3-tuples and 84 such permutations of pairs and triplets of their inverses: e_i^–1 = –e_i. The seven 3-tuples and the seven 3-tuples of their inverses have 168 permutations. The octonion algebra can be represented by the Fano plane because SL(3,2), the simple group of automorphisms of the octonions, is of order 168. Just as the notes in the eight Church musical modes are repeated 168 times in their intervals, so, too, the 14 unit imaginary octonions and their inverses have 168 permutations of their products of two or three.

 

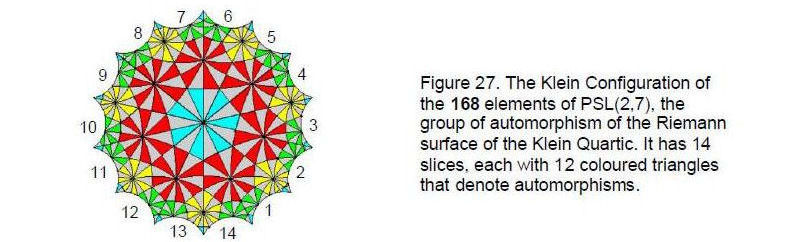
Finally, the association of the number 14 with the number 168 is found in the Klein Configuration, the mapping on the hyperbolic plane of the 168 automorphisms of the Riemann surface of the Klein Quartic:

X³Y + Y³Z + Z³X = 0.

31

It has 168 coloured hyperbolic triangles (Fig. 27) distributed over seven sectors, each divided into two slices. They comprise a {7,3} tiling of 24 heptagons, three meeting at each of its 56 vertices, and each triangle representing a possible automorphism of the Riemann surface. By a theorem due to Hurwitz,¹³ this is the largest number of symmetries possible for a surface of genus 3, such as that of the Klein Quartic. As the 84 permutations of octonions in the seven 3-tuples consist of 12 per 3-tuple and the 84 permutations of their inverses number 12 per 3-tuple, the triangles correspond to permutations and the slices with 12 triangles correspond to 3-tuples, the two slices of each sector corresponding to a 3-tuple of octonions and to a 3-tuple of its inverses. The Klein Configuration with its 14 slices paired into seven sectors displays the same pattern as 1. the grouping of the 14 notes of the Church modes into seven pairs of notes and their complements, 2. the grouping of the 14 meridians into seven Yin/Yang pairs, and 3. the pairing of the 14 roots of G₂ (the group of automorphisms of octonions). This is because the group of 168

Table 3 Sephirah Title  Godname  Archangel  Order of Angels  Mundane Chakra  Kether 620  21  314  833  636  Chokmah 73  15,26  248  187  140  Binah 67  50  311  282  317  Chesed 72  31  62  428  194  Geburah 216  36  131  630  95  Tiphareth 1081  76  101  140  640  Netzach 148  129  97  1260  64  Hod 15  153  311  112  48  Yesod 80  49  246  272  87  Malkuth 496  65,155  280  351  168

symmetries of the Klein Quartic is PSL(2,7), which is isomorphic to SL(3,2), the symmetry group of the Fano plane consisting of seven pairs of points and lines. More reason, therefore, that the Klein Quartic should, as discussed in Article 15,¹⁴ play a fundamental role in M-theory through the connection between octonions and the superstring gauge symmetry group E₈! The true ‘Theory of Everything’ is what underlies the total set of analogous manifestations of the 14-fold, category pattern of holistic systems. It is not just M-theory, which is but one application of this universal conceptual scheme to matter. Physics will not discover what the latter is until it understands the nature of a holistic system. To achieve this, it will need to recognise that the essence of everything is not energy but God.

References
¹ Phillips, Stephen M. Article 16: “The tone intervals of the seven octave species and their correspondence with octonion algebra and superstrings,” (WEB, PDF).

² Phillips, Stephen M. Article 1: “The Pythagorean nature of superstring and bosonic string theories,” (WEB, PDF), p. 5.

³ The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). Table 3 above gives their number values obtained by the practice of gematria, wherein each letter of the alphabet has a number

32

assigned to it, giving a number value to a word that is the sum of the values of its letters. Numbers from this table that are referred to in the article are written in boldface.

⁴ Ref. 2.

⁵ Phillips, Stephen M. Article. 29: “The triakis tetrahedron and the disdyakis triacontahedron embody the fine-structure constant and the structural parameter of the heterotic superstring,” (WEB, PDF), pp. 4–5.

⁶ Phillips, Stephen M. Article 30: “The equivalence of the triakis tetrahedron, disdyakis triacontahedron and Plato’s ‘Lambda tetractys,’” (WEB, PDF), pp. 3, 6, 11.

⁷ Ibid.

⁸ Besant, Annie, and Leadbeater, C.W. Occult Chemistry, 3rd ed., Theosophical Publishing House, Adyar, Madras, India, 1951.

⁹ For example, see: Article 5. “The superstring as microcosm of the spiritual macrocosm,” (WEB, PDF), pp. 7–10.

¹⁰ Phillips, Stephen M. Article 27: “How the disdyakis triacontahedron embodies the structural parameter 1680 of the E₈×E₈ heterotic superstring,” (WEB, PDF), p. 17.

¹¹ Ref. 5, p. 9.

¹² Phillips, Stephen M. Article 15: “The mathematical connection between superstrings and their micro-psi description: a pointer towards M-theory,” (WEB, PDF), p. 10–12.

¹³ Hurwitz, A. “Über algebraische Gebilde mit eindeutigen Transfomationen in sich,“ Math. Ann. 41 (1893), 403–442.

¹⁴ Ref. 11, pp. 24–28.

33