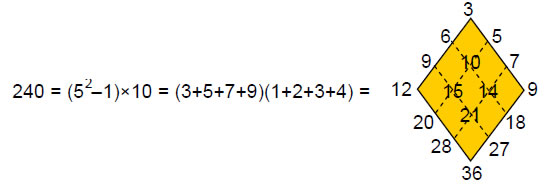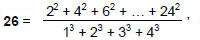ARTICLE 29

by

Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

 

Abstract

1

Article 28 showed that an isomorphism exists between the disdyakis triacontahedron with 62¹ vertices and the two sets of the last six polygons of the inner Tree of Life whose 62 corners are unshared with its outer form. It allowed the root structure of the superstring gauge symmetry group E₈ and its subgroups E₇ and E₆ to be correlated with the icosahedron and dodecahedron within this polyhedron. This article will reveal further ways in which parameters of particle physics are embodied in it. Three ways of constructing polyhedra with triangular faces from tetractyses will be discussed (labelling of cases follows discussion in previous articles):

Case B: Internal triangles divided into three tetractyses; polygonal faces divided into three tetractyses;
Case A: internal triangles divided into three triangles; faces turned into one tetractys;
Case C: internal triangles turned into tetractyses; faces turned into tetractyses;
(The fourth possibility in which internal triangles are turned into tetractyses and faces divided into three tetractyses need not be considered for the current purpose).

Table 2. Formulae for the three types of construction of polyhedra with triangular faces.

	Case C	Case A	Case B
Surface
Number of vertices surrounding axis =	C–2	C–2	C+F–2
Number of edges surrounding axis =	E	E	E+3F
Number of triangles surrounding axis =	F	F	3F
Subtotal =	2E	2E	2E+6F
Interior
Number of vertices surrounding axis =	0	E	E
Number of edges surrounding axis =	C–2=E–F	C–2+3E=4E–F	C–2+3E=4E–F
Number of triangles surrounding axis =	E	3E	3E
Subtotal =	2E–F	8E–F	8E–F
Total =	4E–F	10E–F	10E+5F

Definitions
C = number of vertices of polyhedron.
E = number of polyhedral edges.
F = number of polyhedral faces.
C, E & F are related by Euler’s formula for a convex polyhedron:

C – E + F = 2.

m	=	number of triangular sectors of a face with m edges.
n(m)	=	number of faces with m sides.
L	≡	Σmn(m) = number of triangular sectors of faces.
		m

The internal triangles formed by the centre of the polyhedron and the two ends of an edge are turned into single tetractyses. Triangular sectors of faces are turned into tetractyses.

Surface

Number of vertices in faces = C + F = 2 + E.
Number of edges in faces = E +		Σmn(m) = E + L.
		m
Number of triangles in faces = L.
Number of vertices, edges & triangles = 2 + E + E + L + L = 2E + 2L + 2.
Interior
Number of vertices = 1.

 

 

 

 

 

2

Number of edges = C.
Number of triangles = E.
Number of vertices, edges & triangles = C + E + 1 = 2E – F + 3.
Total number of vertices, edges & triangles = 4E – F + 2L + 5.
The number ‘5’ denotes the five geometrical elements making up the axis (three vertices and two edges). The number of geometrical elements in the surface of the polygon that surround the axis ≡ S = 2E + 2L. The number of internal elements surrounding the axis ≡ I = 2E – F. The total number of elements surrounding the axis ≡ N = S + I = 4E – F + 2L.

E = 18 and F = 12 for the triakis tetrahedron and E = 180 and F = 120 for the disdyakis triacontahedron, that is, these numbers are ten times as large in each case. Table 2 indicates that the numbers of geometrical elements of each kind surrounding the axis either inside or on the faces of a polyhedron with triangular faces depends only on the value of E and F. This means that, for the disdyakis triacontahedron, the number of internal or external geometrical elements of each kind is always ten times the corresponding number for the triakis tetrahedron. The ten-fold property is unique to this pair of Catalan solids because no other pair has E and F differing by a factor of 10.

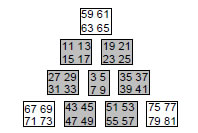
Table 3. List of values of S, I and N for the Archimedean and Catalan solids.

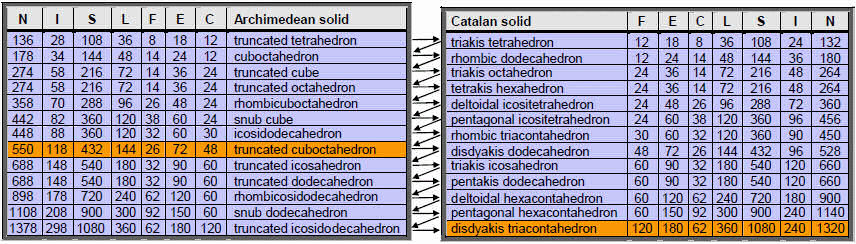
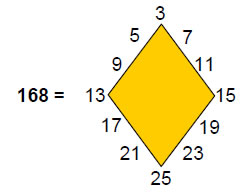
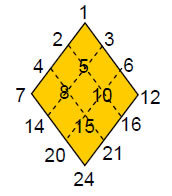
Starting with the truncated tetrahedron (the polyhedron with the least number of faces), and counting down these tables in a zigzag fashion across pairs of dual polyhedra listed in order of increasing C, the 15th polyhedron picked out by the Godname YAH with number value 15 is the truncated cuboctahedron and the 26th (and last) polyhedron picked out by the complete Godname YAHWEH with number value 26 is the disdyakis triacontahedron (both shown in Table 3 with orange cells. We now know the significance of the latter: it is the polyhedral counterpart of 10 overlapping Trees of Life. However, what is the significance of the truncated cuboctahedron? Table 3 shows that 550 vertices, edges & triangles surround its axis, where

550 =

55 55      55 55      55      55 55      55      55      55

 

and

55 =	1 2    3 4    5    6 7    8    9    10 .

 

3

The Decad (10) — the Pythagorean measure of perfection — determines the number of geometrical elements in the truncated cuboctahedron. As discussed in Article 3,² the map of all levels of reality, called the ‘Cosmic Tree of Life’ (CTOL), consists of 91 overlapping Trees of Life, the seven lowest ones representing 26-dimensional spacetime. CTOL has 550 Sephirothic emanations.³ The truncated cuboctahedron is unique among the Archimedean and Catalan solids in being made up of the same number of geometrical elements as there are Sephirothic levels in the map of the spiritual cosmos.

The counterpart of this beautiful property in the Platonic solids is the fact that they have 550 vertices, edges & triangles in their 50 faces.⁴ Its counterpart in the dodecahedron is the fact that, when constructed from tetractyses, it has 550 hexagonal yods.⁵

The number 550 is always embodied in objects that possess sacred geometry. For this reason, it is no coincidence that the polyhedron is the 15th in the sequence of Archimedean and Catalan solids, as prescribed by YAH.

According to Table 3, the disdyakis triacontahedron has 1320 geometrical elements surrounding its axis, that is, 1260 geometrical elements other than the 60 vertices that surround it. This is the number of yods in 126 tetractyses. Remarkably, 126 is the sum of the number values of the four types of combinations of the letters A, H and I in EHYEH (AHIH), the Godname of Kether:

A = 1, H = 5, I = 10
1. 2. 3. 4.	A + H + I AH + HI + AI + HH AHI + HIH + AHH AHIH	=   16  =   42  =   47  =   21
	Total	= 126

Just as remarkable is the fact that there are 1260 yods on the edges of the 360 tetractyses in the 120 faces of the disdyakis triacontahedron.⁶ This illustrates how EHYEH prescribes the disdyakis triacontahedron.

The 1320 geometrical elements surrounding the axis of this polyhedron comprise 660 (=66×10) elements and their mirror ages. As 66 is the 65th integer after 1, the Godname ADONAI of Malkuth with number value 65 prescribes the disdyakis triacontahedron. Similarly, it prescribes the triakis tetrahedron with 66 elements surrounding its axis.

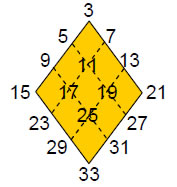
We showed in Article 27 that the number of geometrical elements of a given type surrounding the axis of the disdyakis triacontahedron is ten times the number of like elements in the triakis tetrahedron for case A and case B. Inspection of Table 3 shows that this is true also for case C. The triakis tetrahedron has 132 elements surrounding its axis, which consists of five elements. The polyhedron is therefore built from 137 geometrical elements. Three remarkable properties emerge:

Case A:168 elements surround its axis, where 168 is the number of roots of the superstring gauge symmetry group E₈ that do not belong to its subgroup E₆;
Case B: 240 elements surround its axis, where 240 is the number of roots of E₈;
Case C: it possesses 137 elements.

Physicists regard 137 as, perhaps, the most important number in physics because, as the measure of the strength of the electromagnetic interaction between an electron and an electromagnetic field, the fine structure constant e²/ħc ≈ 1/137 determines the very nature and size of atoms, as well as the chemistry of materials arising from their mutual

4

bonding. The simplest construction of the triakis tetrahedron from tetractyses (case C) requires 137 geometrical elements. The Pythagorean Tetrad determines this number because 137 is the 33rd prime number, where 33 = 1! + 2! + 3! + 4!, and 33 is the 16th odd integer after 1 that can be assigned to a 4×4 array (read across the rhombus):

The next simplest construction of the triakis tetrahedron (case A) require 168 geometrical elements surrounding its axis, where 168 is the sum of the 12 odd integers after 1 that form the edges of a rhombus, four to a side:

The last construction (case B) requires 240 elements surrounding its axis, where

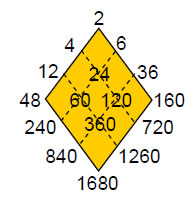
is the sum of the 16 integers that can be assigned to a 4×4 array, starting with the first four odd integers after 1 and adding multiples of them by 2, 3 & 4. It is remarkable that the largest number in the 4×4 array of the first 16 highly composite numbers* is 1680, which is the number of geometrical elements surrounding the axis of the disdyakis triacontahedron in case A:

___________________________________

*An integer is highly composite if it has more factors than all integers smaller than it.

5

If the first 16 factors of 1680 are arranged in a 4×4 array, 24 is the largest one:

This means that 240 is the largest of the first 16 divisors of 1680 multiplied by 10:

This demonstrates that the numbers 168, 240 and 1680 have an arithmetic connection as well as a geometrical one. It exists because these numbers are group-dynamical and structural parameters of the E₈×E₈ heterotic superstring, as explained shortly.

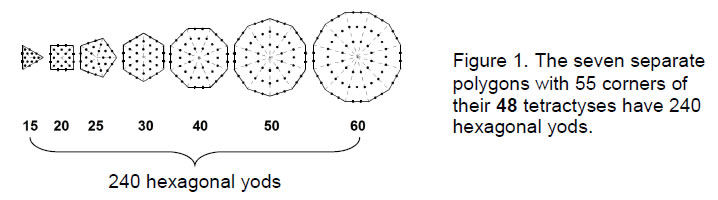
The counterpart in the inner Tree of Life of the 240 geometrical elements surrounding the axis of the triakis tetrahedron in case B are the 240 yods in the seven separate regular polygons other than the 55 corners of their 48 sectors  (Fig. 1). The inner form of ten Trees of Life consists of 70 separate polygons with 2400 hexagonal yods and 550 corners of their 480 tetractyses.

The 550 elements shaping the truncated cuboctahedron in case C correspond to the 550 corners that shape the polygons. The 2400 elements shaping the disdyakis triacontahedron in case B correspond to the 2400 yods other than these corners. As

2400 = 49² – 1 = 3 + 5 + 7 +…+ 97,

2400 is the sum of the 48 odd integers after 1. Their average value is 50, the number value of ELOHIM, Godname of Binah. 49 is the number value of EL CHAI, the Godname of Yesod. The physical meaning of the number 240 is the 240 gauge fields of E₈ associated with its 240 non-zero roots. As each gauge field has 10 space-time components, the 240 fields have 2400 space-time components. Each one is symbolised by a hexagonal yod in the 70 separate polygons of the inner form of ten Trees of Life.

6

7

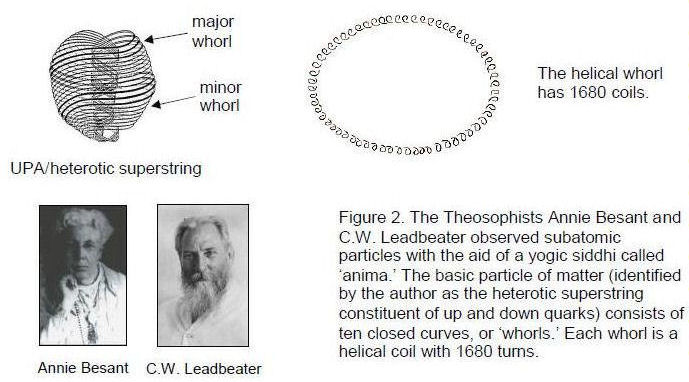
For case A, there are 1680 geometrical elements surrounding the axis of the disdyakis triacontahedron. They are degrees of freedom that appear in the subatomic world as the 1680 circular turns in each “whorl” of the basic unit of matter described paranormally by Annie Besant and C.W. Leadbeater⁷ and interpreted by the author as circularly polarised oscillations of a standing wave (Fig. 2). Ten of these constitute the closed, E₈×E₈ heterotic superstring. Three so-called “major” whorls are thicker than the seven “minor” ones.

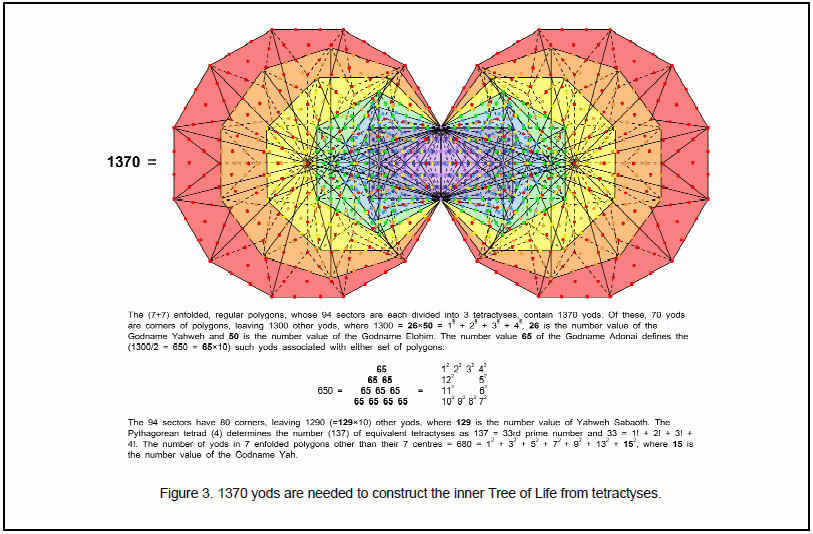
The counterpart in the inner Tree of Life of the 137 geometrical elements needed to construct the triakis tetrahedron is the fact that 1370 yods are needed to build the two sets of seven enfolded polygons when their 94 sectors are divided into three tetractyses (Fig. 3). They are in 282 tetractyses, where 282 is the number value of Aralim,(“thrones”), the Angelic Order assigned to Binah. The fact that yods in 137 tetractyses fill the inner Tree of Life proves the number 137 to be archetypal, as shown by its ubiquitous presence in atomic, nuclear and particle physics. The

correspondences:

1370 yods of inner Tree of Life 1370 geometrical elements of ten triakis tetrahedra        
1320 elements of disdyakis triacontahedron 1320 geometrical elements surrounding axes of ten triakis tetrahedra

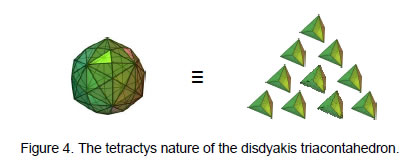
show that the disdyakis triacontahedron is equivalent to ten triakis tetrahedra (Fig. 4), whose number of geometrical elements is equal to the number of yods making up the inner Tree of Life. Each yod symbolizes one of these elements. This is further

8

evidence that the disdyakis triacontahedron is the polyhedral counterpart of the inner Tree of Life, as discussed in Articles 22-24.⁸

Consider those Catalan solids whose faces are triangular as built from tetractyses, with the interior triangles regarded as single tetractyses (case C). The formulae for the various types of geometrical elements composing the solids are shown below:

Number of vertices ≡ V = C + 1. Number of vertices surrounding axis ≡ V' = C – 2.
Number of edges ≡ e = C + E. Number of edges surrounding axis ≡ e' = C + E – 2.
Number of triangles ≡ T = E + F. Number of triangles surrounding axis = E + F.
Total number of geometrical elements ≡ N = 2C + 2E + F + 1 = C + 3E + 3.
Number of geometrical elements surrounding axis ≡ N' = C + 3E – 2.

Table 4 lists the numbers of elements of each type (Catalan solids without triangular faces have dashes in cells):

Table 4. Numbers of geometrical elements in the Catalan solids.

Catalan solid	V	V'	e	e'	T	N	N'
triakis tetrahedron	9	6	26	24	30	65	60
rhombic dodecahedron	-	-	-	-	-	-	-
triakis octahedron	15	12	50	48	60	125	120
tetrakis hexahedron	15	12	50	48	60	125	120
deltoidal icositetrahedron	-	-	-	-	-	-	-
pentagonal icositetrahedron	-	-	-	-	-	-	-
rhombic triacontahedron	-	-	-	-	-	-	-
disdyakis dodecahedron	27	24	98	96	120	245	240
triakis icosahedron	33	30	122	120	150	305	300
pentakis dodecahedron	33	30	122	120	150	305	300
deltoidal hexacontahedron	-	-	-	-	-	-	-
pentagonal hexacontahedron	-	-	-	-	-	-	-
disdyakis triacontahedron	63	60	242	240	300	605	600

Table 3 indicates that, when their triangular faces are divided into three tetractyses, 240 geometrical elements inside the disdyakis triacontahedron surround its axis and 24 internal elements surround the axis of the triakis tetrahedron. Table 4 shows that, when their faces are single tetractyses (case C), the triakis tetrahedron is built from 30 tetractyses with 24 edges and the disdyakis triacontahedron is constructed from 300 tetractyses with 240 edges. For case B, the total number of geometrical elements surrounding their axes are, respectively, 240 and 2400. The counterpart of this pattern in the heterotic superstring shown in Fig. 2 are the 240 gauge charges corresponding to the 240 roots of the gauge symmetry group E₈ that are spread around each of the ten whorls of the UPA, 24 to a whorl. The disdyakis triacontahedron is the polyhedral counterpart of the heterotic superstring and the triakis tetrahedron is the polyhedral counterpart of a whorl, its 24 shape-determining edges surrounding its axis being the geometrical counterpart of the 24 gauge charges carried by each whorl of the UPA.

This analogy can be extended to the very dimensions of space-time predicted by string theory. Table 4 indicates that the triakis tetrahedron has 26 edges, showing how it is prescribed by YAHWEH with number value 26. Two of these edges form the central axis, leaving 24 edges surrounding it. The former correspond to the longitudinal dimension (distance measured along the length of a string) and to the time dimension, whilst the latter are the counterpart of the 24 dimensions of 26-dimensional space-time

9

that are transverse to the string. The number 26 is related to the number 24 as

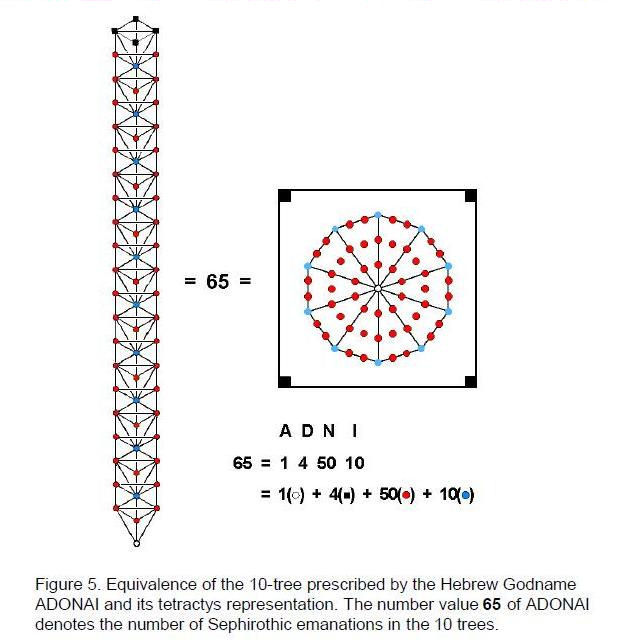
where 24 =1×2×3×4. Appropriately, the Godname ADONAI of Malkuth (the physical aspect of the Tree of Life) prescribes the triakis tetrahedron as the polyhedral form of the fundamental component of the superstring — the whorl — because its number value 65 is the number of geometrical elements from which this Catalan solid is built (see Table 4). The counterpart of this in the Tree of Life are the 65 Sephirothic emanations in the lowest ten Trees of Life belonging to CTOL (Fig. 5).

Below their top are 1680 yods contained in 385 tetractyses (Fig. 6), where

385 =

12 22  32 42  52   62   72  82  92 102 .

This demonstrates how ADONAI prescribes both the ten trees representing the 10-dimensional space-time of superstrings and the 1680 circularly polarised oscillations of each whorl of the heterotic superstring, their counterpart in the disdyakis triacontahedron being the 1680 geometrical elements surrounding its axis in case A.

10

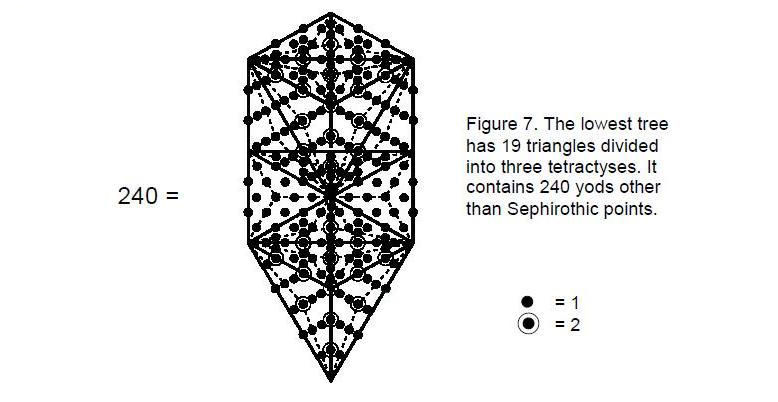
11

The disdyakis triacontahedron in case C has 240 edges surrounding its axis. They are symbolized in the lowest Tree of Life in CTOL as the 240 extra yods generated by conversion of each of its 19 triangles into three tetractyses (Fig. 7). The number 240 expresses in both contexts the number of degrees of freedom needed to form the object, given in the former its essential 11 Sephirothic points and in the latter the axis of the polyhedron made up of five geometrical elements (three vertices & two edges). A yod is at the centre of each of the 300 triangles inside and on the

faces of the disdyakis triacontahedron, which has 60 vertices surrounding its axis. Each of the 240 edges has two hexagonal yods between its ends. The number of yods surrounding the axis of the disdyakis triacontahedron in case C = 300 + 60 + 240×2 = 840 = 84×10, where

84 = 1² + 3² + 5² + 7²

and

10 = 1 + 2 + 3 + 4.

This demonstrates how the Tetrad Principle determines the yod population of this polyhedron as the number of tetractyses with the same number of yods. The next level of differentiation of the tetractys — the 2nd-order tetractys shown in Fig. 8 — has 84 yods surrounding its centre. The meaning of this is that a holistic system patterned or structured according to the Tree of Life blueprint needs 84 degrees of freedom to manifest at the level symbolised by the (○) yod at  the centre of the 2nd-order tetractys.

We saw in Article 27⁹ that the polyhedral example of this is the tetrahedron, which in case B requires 30 triangles with 40 edges and 15 vertices, that is, 85 geometrical elements. 84 of which surround its centre. The 15 yods at corners of

12

the 10 tetractyses in the 2nd-order tetractys symbolize the 15 vertices and the 70 hexagonal yods symbolize the 30 tetractyses and 40 edges. Weighted with the number 10 (the Pythagorean Decad and measure of Wholeness), the 84 yods surrounding the centre of the 2nd-order tetractys generate the number 840. It is the number of yods surrounding the axis of the disdyakis triacontahedron when its interior triangles and faces are turned into tetractyses. The yod at its centre symbolizes this axis.

The number 840 manifests in the heterotic superstring as the 840 circular turns made by each helical whorl as it winds in an outer circuit of 2½ revolutions, making the same number of turns as it returns to its starting point after winding another 2½ times around the spin-axis of the superstring (Fig. 2). As

29² – 1 = 840 = 3 + 5 + 7 + … + 57,

the number 840 is the sum of the first 28 odd integers after 1. This means that the number 8400 can be thought of as the sum of ten identical sets of 28 odd integers, that is, as the sum of 280 odd integers. There are 8400 circular turns in the ten whorls as they wind 2½ times in either the inner or the outer half of the superstring. The number value 280 of Sandalphon, Archangel of Malkuth, determines the number of turns in 2½ revolutions of all ten whorls and the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth — the same Sephirah — is the number of turns in a half-revolution of each whorl. As

41² – 1 = 1680 = 3 + 5 +7 +... + 81,

1680 is the sum of the first 40 odd integers after 1. As

13² – 1 = 168 = 3 + 5 + 7 +… + 25,

168 is the sum of the first 12 odd integers after 1. These properties allow the number 1680 to be represented as a tetractys array of quartets of successive odd integers:

The sum of the ten quartets of odd integers is 1680. The sum of the seven quartets of odd integers shown shaded is 840, as is the sum of the quartets of integers at the corners. The 3:7 division of the tetractys array manifests in the heterotic superstring as the 840 circular turns in the inner or outer halves of each helical whorl.

The sum of the quartet of integers at its centre is 24. This is the number of gauge charges of the superstring gauge symmetry group E₈ that are spread around each whorl of the heterotic superstring. The sum of the first three quartets of integers is 168, the number of turns in a half-revolution of a whorl, and the sum of the first seven quartets is 840, the number of turns in 2½ revolutions, that is, in half a whorl. The sum of all 10 quartets is 1680, which is the number of turns in a whorl. The sum of the last three quartets of integers at the corners of the array is 840. The distinction between hexagonal yods and yods at corners of a tetractys creates the two halves of the whorl.

Such a beautiful property of the odd integers connecting them to the three-dimensional structure of the superstring cannot be due to coincidence. Rather, it serves to demonstrate the power of the insight expressed in the Pythagorean statement that “form is number.”

29 is the tenth prime number in the tetractys array of such numbers:

13

2
3 5
7 11 13
17 19 23 29 .

This illustrates once again the power of the tetractys to generate numbers that in turn determine other numbers of universal significance, such as the superstring structural parameter 1680 and the number 240 of gauge charges corresponding to the 240 roots of the gauge symmetry group E₈:

240 =

24 24 24 24 24 24   24 24 24 24 .

Indeed, this is not merely a trivial way of representing a factor of 10. The E₈×E₈ heterotic superstring is the physical manifestation of this Pythagorean symbol of holistic systems, each of its ten whorls carrying 24 gauge charges associated with these roots. The superstring exists in 10-dimensional space-time, which is symbolized by a tetractys. The three yods (o) at the corners denote the three large-scale dimensions of space, the six yods () at the corners of a hexagon symbolize the six compactified dimensions and the yod (□) at its centre denotes the dimension of time.

Truly, one can now understand the meaning of the oath sworn by the followers of Pythagoras to their master:

“I swear by the discoverer of the tetractys,
Which is the spring of all our wisdom,
The perennial fount and root of Nature.”

References

Table 1. The number values of the ten Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings. (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest. (Saturn)                  317
	Daath (Knowledge)                  474

14

4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness. (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength. (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light. (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour. (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light. (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame. (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth)                  168

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters.

² Phillips, Stephen M. Article 5: “The Superstring as the Microcosm of the Spiritual Macrocosm,” (WEB, PDF).

³ The number of Sephirothic emanations in n overlapping Trees of Life ≡ N(n) = 6n + 4. N(91) = 550.

⁴ Phillips, Stephen M. Article 3: “The Sacred Geometry of the Platonic Solids,” (WEB, PDF), p. 11.

⁵ Ibid, p. 10.

⁶ Phillips, Stephen M. Article 27: “How the Disdyakis Triacontahedron Embodies the Structural Parameter 1680 of the E₈×E₈ Heterotic Superstring.” (WEB, PDF), p. 18.

⁷ Besant, Annie and Leadbeater. C.W., Occult Chemistry, Theosophical Publishing House, Adyar, Chennai. India, 1951.

⁸ Phillips, Stephen M. Article 22: “The Disdyakis Triacontahedron as the 3-dimensional Counterpart of the Inner Tree of Life;” Article 23: “The ‘Polyhedral Tree of Life;” Article 24: “More Evidence for the Disdyakis Triacontahedron as the 3-dimensional Realisation of the Inner Tree of Life and its Manifestation in the E₈×E₈ Heterotic Superstring.” (WEB, PDF).

⁹ Ref. 6, pp. 2-3.

15