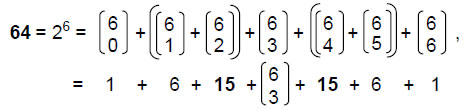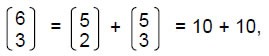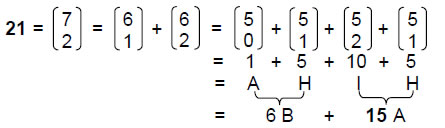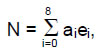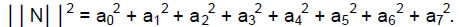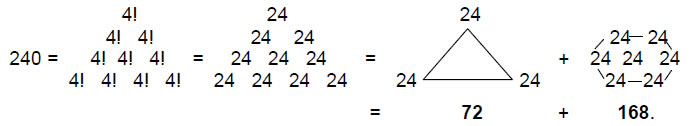ARTICLE 28
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
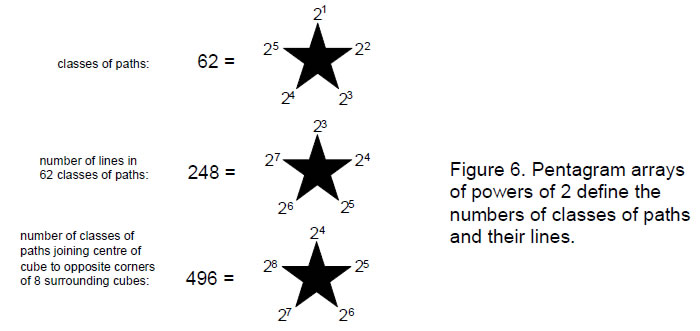
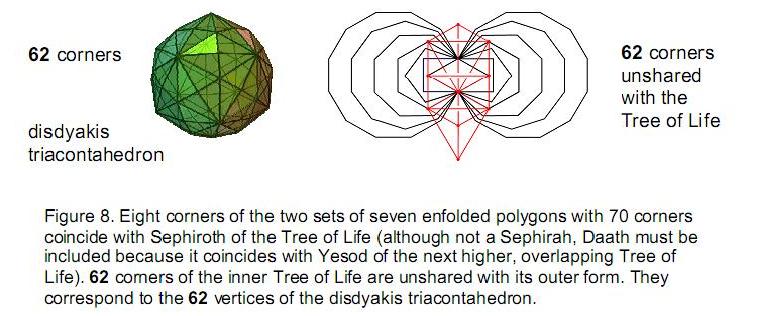
62 types of path join diagonally opposite corners of a cube other than direct ones and paths that connect all its corners. They comprise 248 lines joining pairs of corners. 496 such types of path connect any point in 3-dimensional space to the opposite corners of the eight cubes that surround it. As these corners are vertices of two interpenetrating tetrahedra, there are (248+248) types of paths joining the (4+4) vertices of the pair of tetrahedra. The 62 classes of path correspond to the 62 vertices of the disdyakis triacontahedron. 20 classes of paths that join opposite corners by passing through 3 other corners consist of 80 lines. They correspond to its 20 dodecahedral vertices. 42 classes joining opposite corners by 1, 2, 4 or 5 corners comprise 168 lines. They correspond to the 12 icosahedral vertices and to the 30 centres of the faces of the rhombic triacontahedron formed by these 32 vertices. The 80:168 division of lines corresponds to the 168 yods above the 80 yods in the lowest tree up to the 31st emanation in five overlapping Trees of Life. The same division manifests in the 62 corners of the last (6+6) polygons of the inner form of the Tree of Life that are unshared with its outer form and of which the 62 vertices of the disdyakis triacontahedron are their 3-dimensional counterparts. 80 yods belong to the square and decagon, the pair of which has 20 corners outside their shared edge corresponding to the 20 dodecahedral vertices. 168 yods belong to the four other polygons with 21 corners corresponding either to icosahedral vertices or to centres of faces of the rhombic triacontahedron. The (248+248) yods in the last (6+6) polygons with 62 unshared corners symbolize the (248+248) roots of the gauge symmetry group E8×E8 of heterotic superstrings. The 133 yods associated with the square, pentagon, hexagon and decagon symbolize the 133 roots of E7, the largest, exceptional subgroup of E8. The 78 yods in the square and decagon denote the 78 roots of E6, the rank-6, exceptional subgroup of E8. Both the disdyakis triacontahedron and the last (6+6) polygons embody in a natural way the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth, which is the structural parameter of heterotic superstrings. A profound analogy exists between the inversion symmetry of the intervals of the seven musical scales, the duality of the Platonic solids and the disdyakis triacontahedron that contains them and the numbers of the four division algebras and their inverses. |
1
1. Cube embodies superstring symmetry group parameter 496
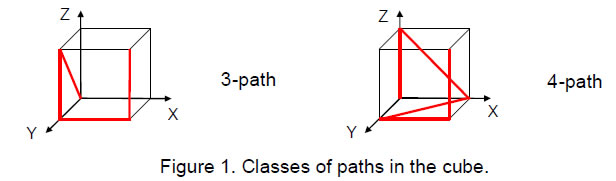
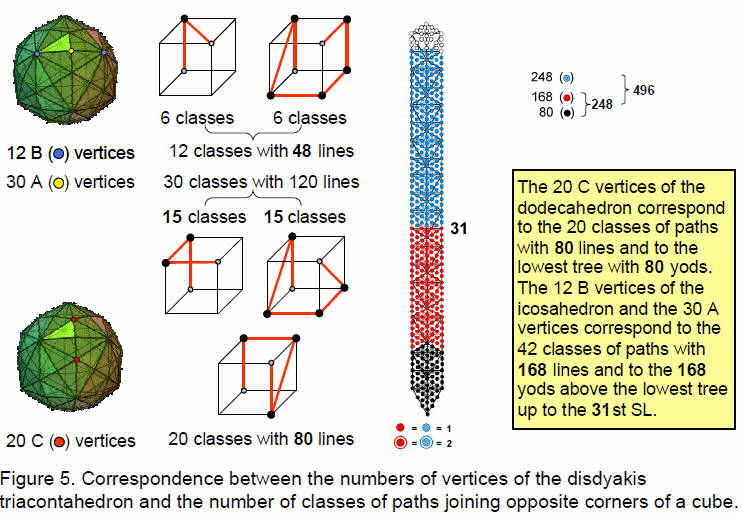
Consider a cube with one corner at the origin of a system of rectangular coordinates whose axes are parallel to its edges (Fig. 1). There are six corners other than this origin and the diagonally opposite corner. There are 6Cn combinations of n corners chosen from this set of six corners. Each group of n corners can be joined in n! ways, each one forming a path made up of (n−1) straight lines. The n! paths constitute a class for each value of n, so that there are 6Cn classes of paths joining the origin to the opposite corner via n corners. These will be called 'n-paths' (n=0-6). n = 0 defines the class comprising a single 0-path made up of one line joining two diagonally
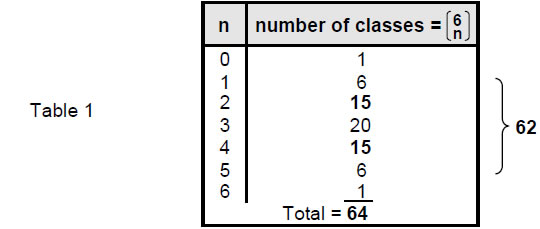
opposite corners and n = 6 defines the class consisting of the 6-paths joining all the eight corners. Table 1 shows the numbers of classes of paths joining opposite corners of a cube:
There are 641 (=43) classes of paths, 62 of them being classes of paths that connect diagonally opposite corners by 1–5 corners.
The origin of the coordinate system is the meeting point of corners of eight cubes (Fig. 2).
If we now imagine paths joining this point to their corners, the number of classes of paths joining the shared corner to opposite corners of the (4+4) cubes = 62(4+4) = 248 + 248 = 496, where 248 is the number of classes of paths joining the origin to the set of four upper or four lower cubes. To every member of the 248 classes of paths joining the origin to diagonally opposite corners of the upper set of cubes, there is its mirror image in the 248 classes of paths joining
2
opposite corners of the lower set of cubes. The division: 496 = 248 + 248 reflects the inversion symmetry of the cube.
Including the single diagonal and the class of paths that join all corners of a cube, the total number of classes of paths = 8×64 = 83 = 29 = 512. There are 256 (=44) classes of paths joining the shared origin to the diagonally opposite corners of the four upper cubes surrounding it; similarly, there are 256 classes of paths joining the origin to diagonally opposite corners of the four lower cubes. There are (512–496=16=42) classes of paths (actually paths) that join the origin to opposite corners by either single lines or by lines connecting all corners.
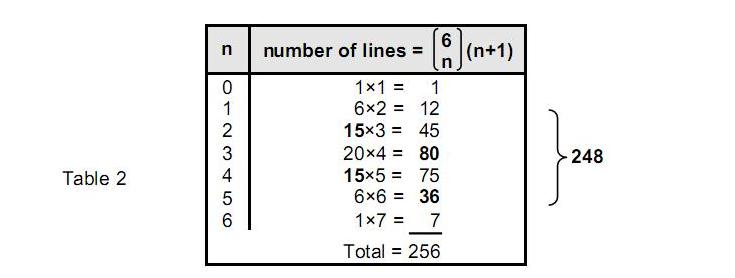
The n-path comprises (n+1) lines. As there are 6Cn n-paths in a class, there are 6Cn(n+1) lines in a class. Their numbers are tabulated below:
The 64 (=43) classes of paths comprise 256 (=44) lines. The 62 classes of paths joining opposite corners via 1-5 corners comprise 248 lines, of which eighty belong to 3-paths joining opposite corners via three corners. Selecting n corners from six corners leaves (6−n) corners. For every combination of the former, there is a corresponding combination of the latter, i.e., 6Cn = 6C6-n. For the former, the number of lines = 6Cn(n+1) and for the latter, the number of lines = 6C6-n(6−n+1). The two numbers are equal only for n = 6 − n, i.e., n = 3. In the special case of three corners, there are 20 classes of 3-paths, each with four lines, totalling 80 lines. We see that the 248 lines
3
comprise 80 lines in 20 classes of a 3-path and 168 lines in 42 classes of 1-, 2-, 4- and 5-paths:
248 = 80 + 168,
where




Of the latter, 12 classes of paths join either one or five corners and comprise 48 lines and 30 classes of paths made up of 120 lines join either two or four corners.
2. Comparison between the disdyakis triacontahedron and cube
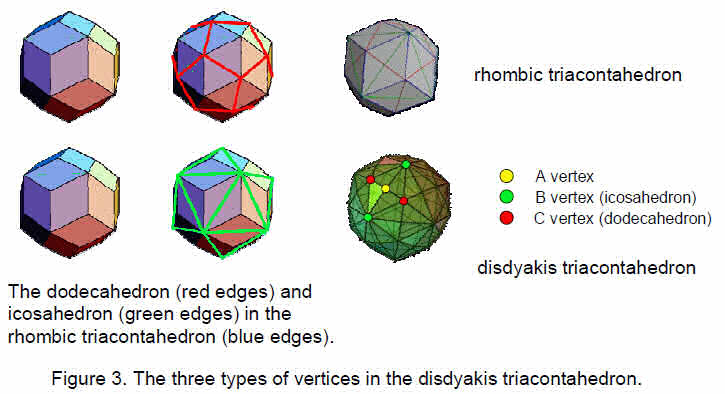
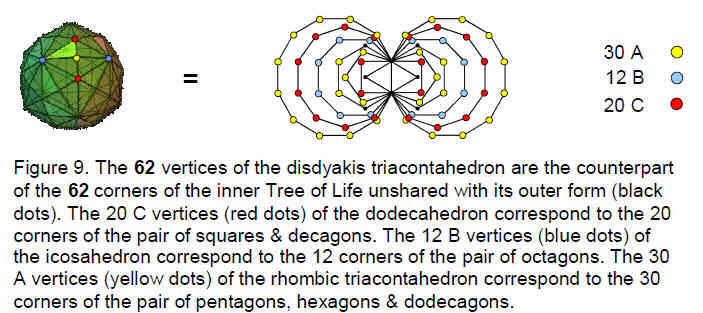
Articles 22–27 established that the disdyakis triacontahedron is the polyhedral counterpart of the inner form of the Tree of Life. Its 62 vertices consists of the 20 (C) vertices of a dodecahedron, the 12 (B) vertices of an icosahedron and the 30 (A) vertices that are raised centres of the 30 faces of a rhombic triacontahedron (Fig. 3). The numbers of the three types of vertices of the disdyakis triacontahedron are the same as the numbers of classes of 3-paths, 2- & 4-paths and 1- & 5-paths:
20 C vertices of dodecahedron 20 classes of 3-paths with 80 lines
12 B vertices of icosahedron 12 classes of 1- & 5-paths with 48 lines
30 A vertices at raised centres
of faces of rhombic triacontahedron30 classes of 2- & 4-paths with 120 lines
This remarkable correlation suggests that the 62 paths in the cube conform to the pattern of the Tree of Life — as already indicated by the fact that they are composed of 248 lines, where 248, being the number of gauge fields of the superstring gauge symmetry group E8, is a Tree of Life parameter, as has been established in previous articles, as well as being the number value of Raziel, the Archangel of Chokmah.
Another sign is the fact that there are seven types of class of paths, of which two
(the 0-paths and 6-paths) comprise eight lines and five (the 1-, 2-, 3-, 4- & 5-paths) comprise 62 classes with 248 lines. This primary 2:5 pattern is characteristic of any mathematical system whose design conforms to the archetypal Tree of Life, for it is the manifestation of the difference between the two Sephiroth of Construction outside the Lower Face — Chesed and Geburah — and the five Sephiroth that form it (Fig. 4). Four classes of path have 168 lines and the fifth has 80 lines. This property reflects the difference between the four Elements Earth, Water, Air and Fire that Kabbalah assigns to the four lowest Sephiroth of Construction and their unitive essence — Aether, or Akasha, the fifth Element, which is assigned to Tiphareth. It is not coincidental that 168 is the number value of Cholem Yesodoth, the Hebrew name of the Mundane Chakra of Malkuth, signifying the Element Earth, the particles of which the ancient Greeks believed have the shape of a cube.
The counterpart in the Tree of Life of the 80:168 division of lines between the 3-path and the 1-, 2-, 4- & 5-paths is shown in Fig. 5. Transformed into tetractyses, the 124
4
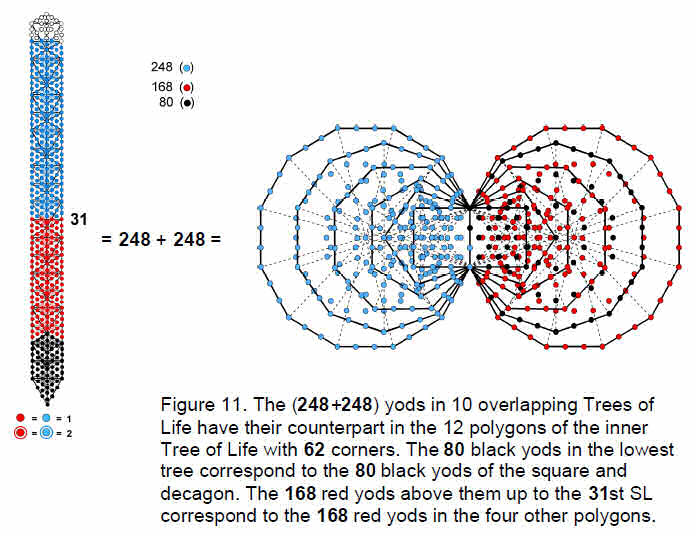
triangles making up ten overlapping Trees of Life have 520 yods, of which there are 496 yods up to (but not including) the 61st SL, the first Sephirah of Construction of the highest tree. There are 248 yods up to (and including) Chesed of the fifth tree, the 31st SL, which is midway in the emanation of these 61 SLs. The 19 triangles of the lowest tree have 80 yods.
Hence, there are 168 yods above the lowest tree up to the 31st SL. As 31 is the number value of EL, Godname of Chesed, it shows how EL prescribes this group-theoretical parameter of the superstring symmetry group E8.
The three types of vertices in the disdyakis triacontahedron have their counterpart in the n-paths of the cube as the classes of 3-paths, 1- & 5-paths and 2- & 4-paths.
The dodecahedron with 20 C vertices corresponds to the 20 classes of 3-paths with 80 lines and to the lowest tree in the ten Trees of Life. The 42 A and B vertices correspond to
5
the 42 classes of 1-, 2-, 4- & 5-paths with 168 lines and to the four trees above the lowest tree up to the midpoint of the ten trees.
The same 80:168 division is generated by assigning the Tetrad 4 to each vertex of the disdyakis triacontahedron. The sum of these numbers is 62×4 = 248. 80 is the sum of the Tetrad assigned to the 20 vertices of the dodecahedron, which we have just seen correspond to the 20 classes of 3-paths. 48 is the sum of the Tetrad assigned to the 12 vertices of the icosahedron, which we saw
correspond to the 12 classes of 1- & 5-paths. 120 is the sum of the Tetrad assigned to the 30 vertices raised above the centres of the rhombic triacontahedron, which correspond to the 30 classes of 2- & 4-paths with 120 lines. The average number of lines per path is always 4 whatever its class.
This ability of the disdyakis triacontahedron to generate the numbers of lines in the three sets of classes as well as the numbers of the latter is remarkable. It demonstrates the existence of an isomorphism between the two polyhedra expressed in both a geometric and an arithmetic way. In terms of the binomial coefficients measuring the numbers of n-paths in a class:
where
so that
64 = (1 + 6 + 15 + 10) + (10 + 15 + 6 + 1) = (1 + 31) + (31 + 1).
The first “1” denotes the 0-path (the one way of joining opposite corners by a diagonal line), the second “1” denotes the 6-path (one way of combining six corners chosen from six corners), the first “31” denotes the 31 classes of 1-paths, 2-paths and the 3-paths joining up to four corners of the cube, and the second “31” denotes the 31 classes of 4-paths, 5-paths and remaining 3-paths. The inversion symmetry of the cube replicates the number of classes of n-paths and (6–n)-paths, whilst the inversion symmetry of the disdyakis triacontahedron replicates its basic set of 31 vertices. The switch over from the upper half to the lower half of this polyhedron takes place in the central (fourth) sheet of vertices, which comprise four As, four Bs and four Cs arranged at the corners of a 12-sided polygon. Starting at the 26th vertex below the apex of the polyhedron,2 there are two As, two Bs and two Cs, making a total of 31 vertices. The remainder of the sheet consists of the inverted images of these six vertices, ending with the 36th vertex below the apex. This indicates how the Godnames YAHWEH with number value 26, EL with number value 31 and ELOHA with number value 36 determine the middle sheet of the disdyakis triacontahedron. The way in which the ten Godnames prescribe this
6
polyhedron is discussed in Article 26.3 The crossover from the first 31 vertices to the second set creates the 32nd vertex as the inverted image of the 31st vertex. Similarly, the 32nd class of path is the 11th of the 20 3-paths. It is the mirror image of the 31st class, the mirror being the diagonal plane parallel to the z-axis that passes through the origin of the cube.
The correspondence between the numbers of vertices and classes is set out below:
The property of the binomial coefficient 6Cn = 6C6-n, which makes the numbers of n-paths and (6-n)-paths equal, has its counterpart in the disdyakis triacontahedron as the fact that every one of its vertices is diagonally opposite one of the type. Just as there are 31 independent classes of n-paths, with the other 31 ones being (6-n)-paths, so there are 31 independent vertices, with the remaining 31 vertices being the mirror images of their counterparts in the first group.
The apex and nadir of the disdyakis triacontahedron correspond, respectively, to the single class of one 0-path (the diagonal joining opposite corners) and the single class of one 6-path, which joins all eight corners of the cube.
In keeping with the seed nature of Kether, the Sephirah to which it is assigned, the Divine Name Ehyeh ("I am") with number value 21 prescribes in a minimal way the shape of the disdyakis triacontahedron because the dodecahedron is the dual of the icosahedron, whilst the rhombic triacontahedron is their combination, so that the six B vertices of the icosahedron and the 15 A vertices centred above the faces of the rhombic triacontahedron (that is, 21 vertices) are all that are required to generate the disdyakis triacontahedron, the remaining 20 C vertices being the centres of the faces of the icosahedron and the remaining six B vertices and 15 A vertices being the mirror images of the minimal set. As confirmation, using the property that nCr = n-1Cr-1 + n-1Cr, the number values of the letters of Ehyeh (AHIH) are binomial coefficients to which the binomial coefficient 7C2 = 21 reduces:
The Godname YAH (YH) assigned to Chokmah with number value 15 prescribes the rhombic triacontahedron as the number of centres of its independent faces, the other 15 faces being their mirror images. The number of A and C vertices is 50. This is the number value of ELOHIM, the Godname of Binah.
3. The three polyhedra define E6, E7 & E8
Projected onto the plane containing the two sets of seven regular polygons as its inner7
form, the Tree of Life shares seven of its Sephiroth and Daath with corners of polygons (Fig. 8). The 62 unshared corners are the counterpart of the 62 vertices of the disdyakis triacontahedron. They consist of two identical sets of 31 corners belonging to the last six polygons:
number of corners = number of yods
outside root edge =The pair of octagons has 12 unshared corners corresponding to the 12 B vertices (Fig. 9). The pair of dodecagons, or the two sets of decagons and squares, has 20 corners corresponding to the 20 C vertices. The squares, pentagons, hexagons and decagons, or the pentagons, hexagons and dodecagons, have 30 corners corresponding to the 30 A vertices.
These 12 enfolded polygons have 490 yods outside their shared root edge, that is, the yods in 49 tetractyses, showing how the Godname EL CHAI of Yesod with number value 49 prescribes these polygons. Each set has 246 yods outside the root edge, showing how the number value of Gabriel, Archangel of Yesod, prescribes this set of polygons whose 31 corners correspond to the primary set of 31 vertices of the disdyakis triacontahedron. Including the four yods of the root edge, there are 248 yods associated with each set, of which 31 are corners that do not coincide with Sephiroth of the Tree of Life when it is projected onto the plane containing the polygons (Fig. 10). This is the counterpart of the fact that, when the triangles in overlapping trees
8
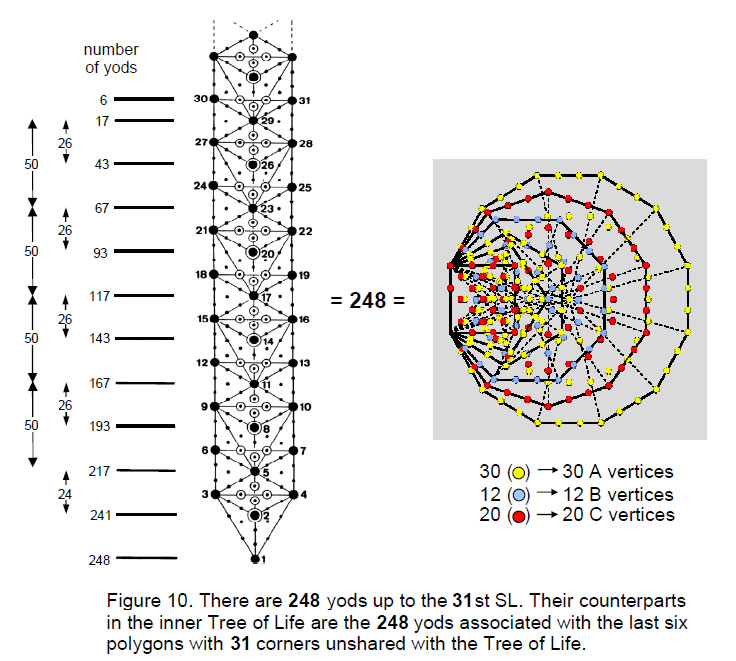
are turned into tetractyses, there are 248 yods up to the 31st SL, as was discussed earlier.
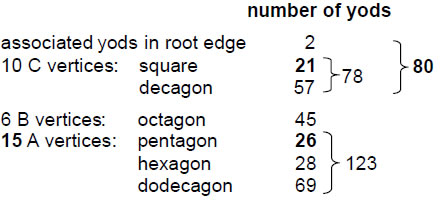
Let us now examine the yod populations of the polygons with the same numbers of corners as the three sets of vertices of the disdyakis triacontahedron. Far from posing a problem of ambiguity, the fact that there are two ways of choosing sets of polygons with corners corresponding to A and C vertices actually tells us how the exceptional subgroups E7 and E6 of E8 are encoded in the inner Tree of Life, as now explained. Consider, firstly, the case where the 20 corners of the squares and decagons correspond to C vertices and the corners of the pentagon, hexagon and dodecagon correspond to A vertices. The yod populations of the polygons are shown below:
We see that 80 yods (78 outside the root edge) are associated with either set of square and decagon with 10 corners. The four other polygons in each set with 21 corners have
9
(123+45=168) yods. The total number of yods associated with each set of polygons is 248, the dimension of the superstring gauge symmetry group E8. The same 80:168 division is found in the yod populations of the polygons as was found earlier for the 248 yods up to the 31st SL of five or more overlapping Trees of Life (Fig. 11), as well as for the 248 lines in the 62 classes of paths connecting opposite corners of a cube. Moreover, just as there are 20 classes of paths with 80 lines, so there are 80 yods associated with each set of square and decagon with 20 corners. Just as there are 42 classes of paths with 168 lines, so the two sets of four polygons with 42 corners have 168 yods in each set.
The square and decagon with 78 yods encode the dimension 78 of E6, the rank-6 exceptional subgroup of E8. As their corners correspond to the 10 independent C vertices of the dodecahedron, we see that the 31 independent vertices of the disdyakis triacontahedron have as their counterpart in the 2-dimensional form of the inner Tree of Life the 31 unshared corners of the last six polygons, whose yods symbolize the 248 gauge bosons of the superstring gauge symmetry group E8 the square and decagon embody the number of gauge bosons of E6. Just as one set of six polygons with 31 corners is the mirror image of the other set with 31 corners, so the first 31 vertices of the disdyakis triacontahedron have 31 other vertices as their inversions. This mirror symmetry generates the direct product structure of two identical symmetry groups E8. The 20 C vertices forming a dodecahedron correspond to its subgroup E6 and the remainder of the polyhedron corresponds to the sector of E8 outside E6.
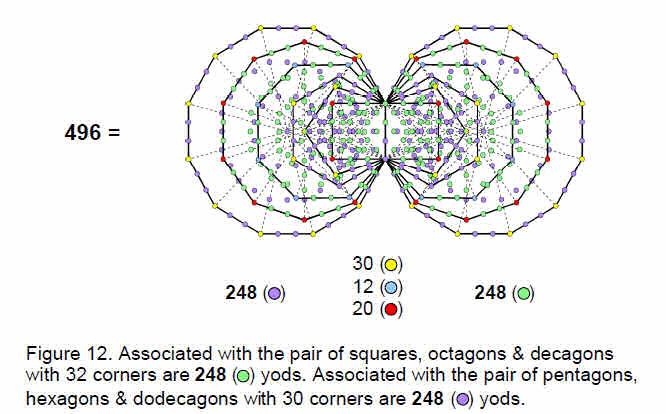
The square, octagon and decagon have (45+78=123) yods — the same as the number of yods in the pentagon, hexagon and dodecagon. As 248 = 2 + 2×123, the number of yods associated with the pair of either set of polygons is 248. Figure 12 shows that the two sets of the last six polygons have 496 yods, reproducing the gauge symmetry group of E8×E8 heterotic superstrings. The 42 corners of the former polygons corresponding to
10
the B and C vertices are coloured either blue or red. The 30 corners of the latter polygons corresponding to A vertices are coloured yellow. As a corner of the pentagon is the centre of the decagon, it is coloured half yellow to indicate that it is one of the 30 corners and half green to indicate that it should be counted with the other green yods in the decagon. In terms of the disdyakis triacontahedron, the dodecahedron and icosahedron with 32 vertices correspond to the pair of squares, octagons and decagons, associated with which are 248 yods.
The 30 vertices raised above the centres of the faces of the rhombic triacontahedron correspond to the 30 corners of the pentagons, hexagons and dodecagons, associated with which are 248 yods.
Now consider the alternative way of choosing polygons with corners corresponding to A and C vertices.
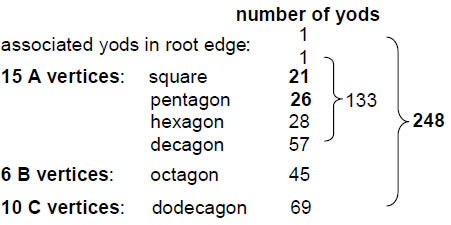
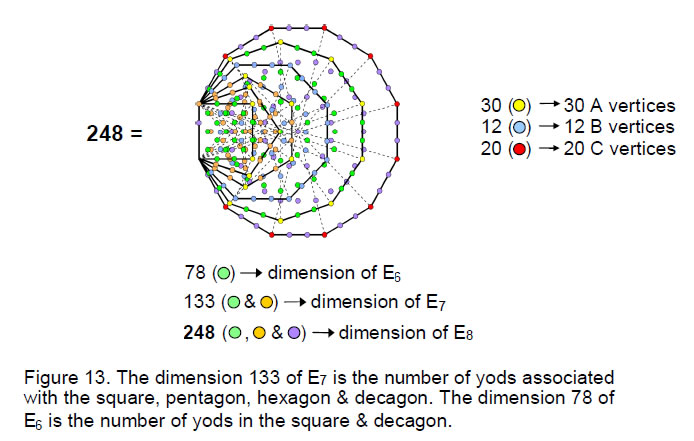
As before, 248 yods are associated with each set of six polygons, two yods on the root edge being associated with each set. The square, pentagon, hexagon and decagon with 15 unshared corners have 132 yods outside their shared root edge. Associating one of the two yods on the root edge with this set of polygons and the other yod with the octagon and dodecagon, we find that 133 yods are associated with the polygons with 15 corners (Fig. 13). This is the dimension of E7, the largest exceptional subgroup of E8. The square and decagon have 78 yods. This is the dimension of E6, the next largest exceptional subgroup of E8.
11
The two ways of choosing a set of polygons with 15 external corners therefore reveal two exceptional subgroups of E8. In one case, E6 is embodied in the polygons with 10 corners corresponding to the dodecahedron. E7 is embodied both in the polygons with 10 corners and in the polygons with 15 corners corresponding to the rhombic triacontahedron. In the other case, E7 is embodied in just the set of polygons that corresponds to the rhombic triacontahedron.
The Godnames EHYEH, YAH and EL prescribe this exceptional group composition as follows:
20 C vertices
20 corners of 2 pairs of squares & decagons
EHYEH: 21 21 corners of pentagon, hexagon, octagon & dodecagon with 168 yods, leaving (2+78) yods of square & decagon. 248 = 80 + 168. YAH: 15 15 corners of pentagon, hexagon & dodecagon with 123 yods. 248 = 2 + 2×123. EL: 31 31 corners of last six polygons with 248 yods. 20 C vertices
20 corners of pair of dodecagons
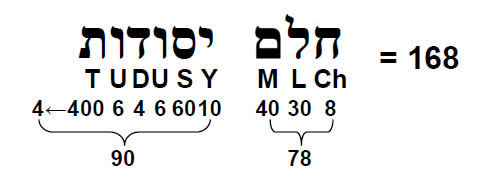
EHYEH: 21 21 corners of square, pentagon, hexagon, octagon & dodecagon with 179 yods. YAH: 15 15 corners of square, pentagon, hexagon & decagon with 133 yods. YH = 10 + 5. 10 corners of square & decagon have 78 yods. EL: 31 31 corners of last six polygons with 248 yods. When constructed from tetractyses, the (7+7) polygons have 80 corners of their 94 tetractyses. Excluding the two triangles with their centres means that the last (6+6) polygons have 78 corners of their 90 tetractyses. The dimension of E6 is therefore embodied in the very geometry of these polygons with 62 corners corresponding to the 62 vertices of the disdyakis triacontahedron. Moreover, the number of corners and triangles making up the polygons = 78 + 90 = 168. This demonstrates powerfully the Tree of Life nature of the last (6+6) polygons, because 78 is the number value of the Hebrew word ‘Cholem’ and 90 is the number value of the Hebrew word ‘Yesodoth’ in
12
Cholem Yesodoth, the Kabbalistic name of the Mundane Chakra of Malkuth:
Whereas the disdyakis triacontahedron was found in Articles 264 and 275 to be built from 900 (=90×10) triangles and their corners and 780 (=78×10) edges, the last (6+6) enfolded polygons consist of 78 corners and 90 triangles. However, it is remarkable how the two numbers 78 and 90 appear in both cases.
This, of course, is not coincidental, for the set of 50 Kabbalistic Godnames, Archangels, Angels and Mundane Chakras constitute a system of transcendental knowledge,
the gematria number values of these words pertaining par excellence to the sacred geometry of the Tree of Life in both its polygonal and polyhedral forms, i.e., the triakis tetrahedron and the disdyakis triacontahedron. The number of edges of the 45 tetractyses making up the last six polygons is 85,6 i.e., 84 edges lie outside their shared edge. The 90 tetractyses of the last (6+6) polygons have (84+84=168) external edges. Once again, this number appears in the geometry of the polygons whose corners correspond to the vertices of the disdyakis triacontahedron. This, too, is not by chance, for many previous articles by the author have shown this number (and its 84:84 division) to appear in discussion of any holistic system that conforms to the design of the Tree of Life. In particular, it is the fundamental structural parameter of the E8×E8 heterotic superstring, being the number of circularly polarised oscillations of each of its 10 whorls as it winds 180° around the axis of spin of the particle. We saw in Section 2 that it is the number of 1-, 2-, 4- & 5-paths whose 42 classes correspond to the 12 vertices of the icosahedron and the 30 centres of the faces of the rhombic triacontahedron.
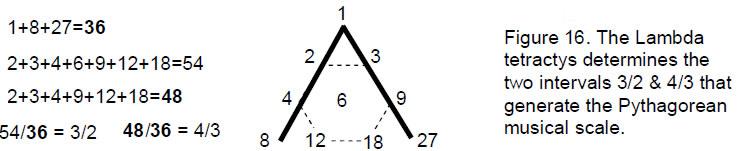
Confirmation that the last (6+6) polygons are a Tree of Life pattern is that, separately, they consist of 90 tetractyses. The Tree of Life parameter 90 has appeared in many contexts in earlier articles. For example, it is the sum of the ten numbers of the so-called ‘Lambda tetractys’ (Fig. 14), whose relative proportions have been known from the time of Plato to be the tone ratios of the notes of the Pythagorean musical scale. The sum of the nine integers surrounding the integer 6 at the centre of the tetractys is 84, where
84 = 12 + 32 + 52 + 72.
As we have just seen, this is the number of external edges of the 45 tetractyses making up each set of the last six polygons. Notice the similarity in character of this number in each context: just as the nine numbers form the boundary of the Lambda tetractys, so the edges of the 45 tetractyses in each set of polygons constitute a boundary.
13
4. The octonion connection
The general form of an octonion is
where ai (i = 0-8) are real numbers, e0 = 1 and ei (i = 1-7) are the unit imaginary octonions with eiej = –ejei and ei2 = -1. The number of linear combinations of eight octonions = 28 – 1 = 255. Of these, seven are the unit imaginary octonions themselves, leaving 248 combinations consisting of the identity 1 and 247 real, linear combinations of two or more unit octonions. This means that there are 248 non-trivial classes of octonions, making them the natural basis for the sought-after M-theory of superstrings whose unified force is mediated by the 248 gauge bosons of E8. The seven imaginary octonions can be combined in 27 – 1 = 127 ways, so that there are 120 linear combinations of two or more. The 248 combinations of unit octonions are of the form:
(i≠j≠k≠l≠m≠n). There are 15 classes of octonions when the imaginary octonions are included. The Godname YAH with number value 15 prescribes how many kinds of octonions there are. Excluding the class of real numbers and the class of unit imaginary octonions leaves 13 classes of real, linear combinations of two or more unit octonions. To every ei, there is its inverse, or conjugate, ei* = -ei, where ei*ei = 1. Similarly, the conjugate of an octonion N is N*, where
N* = a0 – a1e1 – a2e2 – a3e3 – a4e4 – a5e5 – a6e6 – a7e7.
Therefore, 13 classes of octonions are conjugates of their counterparts. The norm of an octonion is ││N││= √N*N, where
The inverse of N ≠ 0 is N–1 ≡ N*/││N││2, so that N–1N = NN–1 = 1. To each of the 13 classes of octonions there is a class of their inverses, so the 26 classes of octonions and their inverses are prescribed by YAHWEH. There are 248 combinations of unit octonions and 248 inverses of them, totalling 496, the dimension of E8×E8.
This pattern is analogous to the 13 members of the Archimedean solids and their duals — the Catalan solids. The analogy is even more apt when one considers that two of the Archimedean solids have mirror images (likewise for the Catalan solids), so that there are 15 Archimedean solids and 15 Catalan solids when these are included. Polyhedral duality has its counterpart in the world of octonions as their inverses, where each inverse is a real, linear combination of the inverses ei* = –ei of the unit imaginary octonions ei. The counterparts of the five Platonic solids are the real numbers, the complex numbers,
14
their inverses, the quaternions and their inverses. Just as the tetrahedron is self-dual, so the set of real numbers is identical to the set of their reciprocals.
The number of linear combinations of n unit octonions is given below:
The 248 combinations other than the 7 imaginary unit octonions consist of 8 combinations of 7 octonions and 240 others, of which 72 consist of the 70 combinations of 4 octonions, one combination of 7 octonions and one combination of 8 octonions. 168 of them consist of combinations of 2, 3, 5 & 6 octonions.
The roots of the E8 algebra can be described in terms of eight orthonormal unit vectors {ui}. Eight zero roots:
correspond to points at the centre of the root diagram and 240 nonzero roots all have length √2. They are given by
and
The 240 non-zero roots of E8 comprise 168 made up of four sets of 28 and one set of
15
56, one set of 70 and two single ones. The 72 non-zero roots are those of E6, the rank-6 exceptional subgroup of E8.
Comparing the root structure of E8 with the types of combinations of octonions, we see an isomorphism exists between them. Even more remarkable is that the same 8:72:168 pattern of zero and non-zero roots and combinations of octonions is exhibited in the last six polygons discussed earlier. We found that the square and decagon have 78 yods, that is, 80 yods when the two yods on the root edge associated with each set of polygons are included. The decagon has eight external corners, leaving 72 yods for the pair of polygons corresponding to the ten C vertices of the dodecahedron. The remaining four polygons corresponding to the six B vertices of the icosahedron and to the 15 A vertices have 168 yods. The following correspondence exists:
1. 8 zero roots
8 combinations of 7 octonions
8 external corners of decagon;
2. 72 non-zero roots of E672 combinations of 4, 7 & 8 octonions
72 yods of square & decagon other than the latter’s corners;
3. 168 non-zero roots of E8 not those of E6168 yods of pentagon, hexagon, octagon & dodecagon.
This demonstrates very clearly that the root composition of E8 manifests in the six polygons, both sets of which have corners that are the counterparts of the 62 vertices of the disdyakis triacontahedron. Each yod symbolises a root, its corresponding group generator and therefore a gauge field of E8 transmitting the unified, E8×E8 heterotic superstring interaction.
When the tetrad (4) is assigned to the 62 vertices of the disdyakis triacontahedron, the sum of these numbers is 248, the dimension of E8. The 20 C vertices of the dodecahedron underlying it define the number 80. This is the number of yods in the square and decagon (including the two yods in the root edge associated with them), whose ten external corners correspond to half the vertices of this Platonic solid. Further more, the 42 A and B vertices define the number 168, which is the number of yods in the other four polygons whose 21 external corners unshared with the Tree of Life correspond to half the number of vertices of the icosahedron and centres of faces of the rhombic triacontahedron. The three polyhedra underlying the disdyakis triacontahedron therefore embody the very pair of numbers 80 and 168 that are yod populations of those polygons with corners corresponding to half their vertices. This remarkable property is an example of the beautiful harmony of number and geometry displayed by the disdyakis triacontahedron.
Physicists working in the field of superstring theory have focussed on E6 as the result of symmetry breaking of E8 because of its attractive features in accounting for the physics of the Standard Model. Such a breakdown of the complete symmetry amounts to selecting from the disdyakis triacontahedron the dodecahedral array of 20 C vertices. If the axis joins an opposite pair of C vertices, the 42 A and B vertices generate through the Tetrad the number 168 and the 18 C vertices surrounding it generate the number 72, the two poles creating the number 8 as the number of zero roots of E8. In its polygonal counterpart, they correspond to the 72 yods of the square and decagon other than the eight external corners of the latter.
Article 27 showed that, when constructed from the tetractys — the basic building block of sacred geometry — the disdyakis triacontahedron has 1680 triangles and their corners and edges surrounding an axis through two opposite vertices.7 When its 120 faces are constructed from three tetractyses instead of one, there are 2400 (=240×10) such geometrical elements. In other words, 720 (=72×10) new elements made up of
16
120 corners, 360 edges and 240 triangles are added to the 1680 (=168×10) elements. The 1680 elements belong to the underlying rhombic triacontahedron when its 30 rhombic faces are each constructed from four triangles whose sides are also edges of internal triangles meeting at its centre. 720 elements are added when this polyhedron is turned into the disdyakis triacontahedron by raising the centres of its faces so that they become 30 new vertices and by constructing the 120 new faces from three tetractyses, not one. Apart from the permitted Pythagorean factor of 10, the division: 240 = 168 + 72 found above is now the result of transforming the rhombic dodecahedron into the disdyakis triacontahedron. Symmetry-breakdown of E8 to E6 amounts to squashing the pyramid faces of the latter until they form the flat, golden rhombic faces of the rhombic triacontahedron. This does not amount to a reduction of rotational symmetry, because both polyhedra possess the same icosahedral group Ih of order 120.
As the symbol of the Pythagorean Tetrad, the tetractys represents the number 240 as
The corners of the tetractys array of the number 24 sum to 72 and the seven remaining numbers add to 168. Many previous articles have discussed the physical significance of this number. As the tenth overtone and the 32nd note after the tonic of the Pythagorean scale, the perfect fifth of the fifth octave has the tone ratio 24, that is, a wavelength that is 24 times as small as the tonic of the first octave. That is its musical connotation.
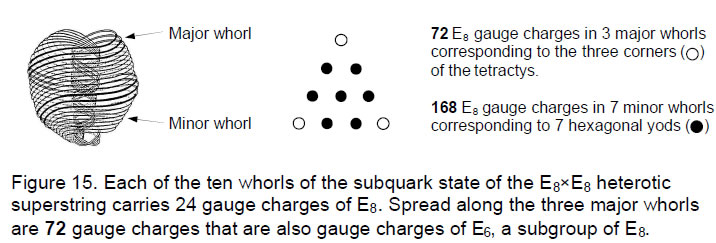
Its significance for superstring theory is that the E8×E8 heterotic superstring (Fig. 15) described by Annie Besant and C.W. Leadbeater with a yogic siddhi called ‘anima’8 consists of ten closed curves, or whorls. Three ‘major’ whorls were depicted by these two Theosophists as thicker and brighter than the seven other ‘minor’ whorls. The author has proposed that 24 gauge charges of E8 corresponding to its roots are spread along each whorl. This means that 72 gauge charges, which are gauge charges of its subgroup, E6, are spread along the three major whorls and the remaining 168 gauge charges are spread along the minor whorls. The difference between the major and minor whorls arises from symmetry-breakdown of E8 to E6. This breakdown is what is signalled by the fundamental 72:168 division described throughout this article. It is embodied in the triakis tetrahedron — the Catalan solid with the least number of vertices — as the 168 geometrical elements surrounding an axis through two vertices and the 72 new elements added when its faces are built from three tetractyses, not one.
17
5. Polyhedral duality, octonion inverses & musical scales
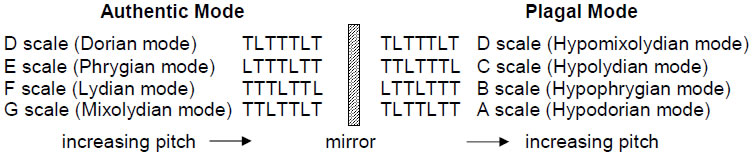
The seven possible musical scales are successive sequences of seven intervals:
T is the tone interval of 9/8 in the Pythagorean musical system, which is slightly larger than the modern equal-tempered tone interval, and L is the leimma of 256/243, corresponding to, but slightly lower than, the modern semitone. The patterns of intervals of the four authentic modes are the mirror images of those of the four plagal modes:
As a musical scale, the Hypomixolydian mode is identical to the Dorian mode, being added to complete the pairs of authentic and plagal modes. It has, however a distinct ethos because its finalis (ending note) and dominant (reciting note) are different. Suppose that each rising interval is replaced by its falling counterpart, i.e., T
T-1 and L
L-1. An ascending scale, e.g., TLTTLTT, then becomes T-1L-1T-1T-1L-1T-1T-1, which is just the descending version of the ascending scale TTLTTLT. Inverting each interval in a scale creates another scale whose pattern of intervals is its mirror image. Only the D scale is its mirror image: TLTTTLT
T-1L-1T-1T-1T-1L-1T-1 = TLTTTLT. This means that the seven distinct musical scales comprise one scale (the Dorian mode) that is invariant with respect to inversion of its intervals and three pairs of scales — A & G, B & F and C & E — that are inversions of each other.
The four classes of real division algebras whose multiplication is associative consist of the self-conjugate real numbers (these include the reciprocal of any given number), the complex numbers and their inverses, the quaternions and their inverses and the octonions and their inverses. These seven sets of numbers are analogous to the seven types of musical scale and to the seven polyhedra consisting of the five Platonic solids, the truncated icosidodecahedron and its dual, the disdyakis triacontahedron:
disdyakis triacontahedron + truncated icosidodecahedron
The musical counterpart of inverse numbers and dual polyhedra is the distinction in church music between authentic and plagal modes — more accurately, the inversion symmetry of their patterns of intervals. The mirror-symmetric D scale corresponds to the self-conjugate, real numbers and to the self-dual tetrahedron. As the mathematically perfect Pythagorean scale, the C scale corresponds to the most general class of
18
numbers whose addition and multiplication obey the rule of association and to the most complex of the Catalan solids — the disdyakis triacontahedron. Because the Archimedean solids were discovered nearly 2000 years before the Catalan solids, mathematicians are used to thinking of the latter as the duals of the more familiar Archimedean solids instead of vice versa, although each family is really the dual of the other. To maintain, however, the formal correspondence with the four classes of numbers and with the four authentic modes, it is more correct to think of the family of Catalan solids as primary (although only in this sense and not for any mathematical reason), so that the disdyakis triacontahedron corresponds to both the octonions and the perfect Pythagorean scale rather than to, respectively, their inverses and the Phrygian mode (E scale). On the other hand, the four authentic modes (the D-, E-, F- & G-scales) were regarded as primary and given the names inherited from ancient Greece, whilst their plagal counterparts — the ‘hypo’ versions — were added as a counterpoint. As the mathematically perfect, Pythagorean (C) scale is a plagal mode (the Hypolydian), the natural requirement that it should correspond to the disdyakis triacontahedron would make the plagal modes assume a pre-eminence that, historically, they never had. As with the polyhedra, the historical sequence of discovery is not necessarily the correct guide to what is the correct order of unfolding in the archetypal world. It is wiser to ignore the order of cultural manifestation of different forms of the divine paradigm when one examines how the universal principle of correspondence relating these works out in detail. History can be an unreliable guide.
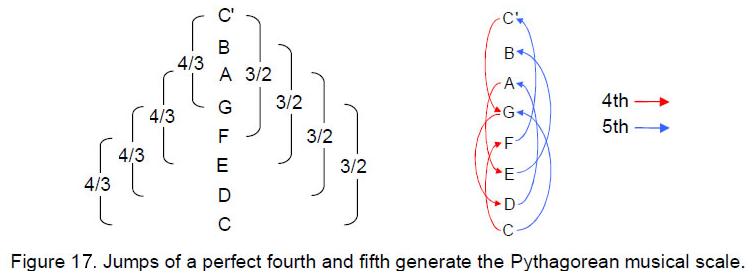
Other examples of duality/inversion are discussed in Article 19.9 The perfect fourth and the perfect fifth of the musical scale can be thought of as duals of each other. If we start with a given note, raise its pitch by a perfect fourth and then by a perfect fifth (or vice versa), we end up with the same note of the next higher octave. In an analogous way, if we start with a given polyhedron, interchange its corners and faces and then interchange the corners and faces of the dual polyhedron we have created, we end up with the polygon with which we started. Raising a note with tone ratio n by a perfect fifth is equivalent to lowering it by a perfect fourth, the two resultant notes: (3/2)n and (3/4)n, merely being the same note an octave apart because (3/2)n/(3/4)n = 2. Similarly, the inverse of the inverse of an octonion is the octonion itself: (N–1)–-1= N.10 Just as the product of the intervals of a perfect fourth and perfect fifth is an octave higher, i.e., 4/3×3/2 = 2, so the product of an octonion and its inverse is unity, i.e., NN–1 = 1.
Despite the product being 2 in the former case and 1 in the latter, both express the same kind of identity, for a musical tone has the same quality, whatever its octave. The same relationship of reciprocity is exhibited in the four pairs of authentic and plagal modes, in polyhedra and their duals and in number theory as the numbers of the four division algebras and their inverses. Projective planes* also display a duality whereby they
____________________________
*A finite projective plane of order n is a set of (n2 + n + 1) points and the same number of lines such that 1. given any two distinct points, there is exactly one line incident with both of them, 2. given any two distinct lines, there is exactly one point incident with both of them, 3. there are four points such that no line is incident with more than two of them.
19
remain the same when their points and lines are interchanged. The simplest projective plane is the Fano plane of order 2. It represents the algebra of octonions.11
The tetractys underlying Plato’s Lambda generates the perfect fifth because the sum of the integers at its corners is 36 and the sum of the seven integers arranged at the corners and centre of a hexagon is 54, where 54/36 = 3/2 (Fig. 16). It also generates the perfect fourth because the sum of the integers surrounding the central integer 6 is 48, and 48/36 = 4/3. The distinction between the Supernal Triad and the seven Sephiroth of Construction, symbolized in the tetractys as the three yods at its corners and the seven ‘hexagonal’ yods, generates through the Lambda tetractys all the notes of the Pythagorean musical scale by continuous, alternating jumps of
four perfect fourths and three perfect fifths, starting from the tonic C (Fig. 17).
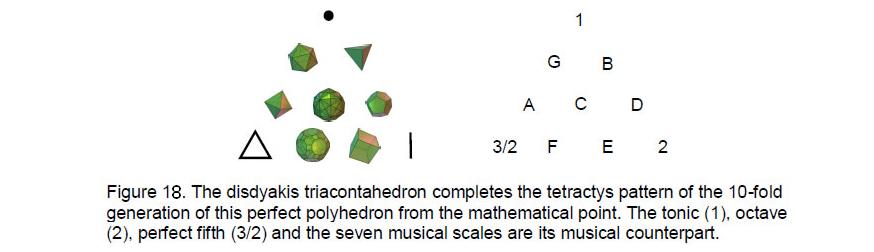
Just as the tonic, perfect fifth (or perfect fourth) and octave form the basis of the musical diatonic scale and generate the seven musical scales culminating in the perfect C scale, so the point, line and triangle are the three basic geometrical elements whose
Pythagorean scale, so combinations of points, lines and triangles generate the seven polyhedral counterparts of these scales, namely, the five Platonic solids, the truncated icosidodecahedron and its dual, the disdyakis triacontahedron, which is the Catalan
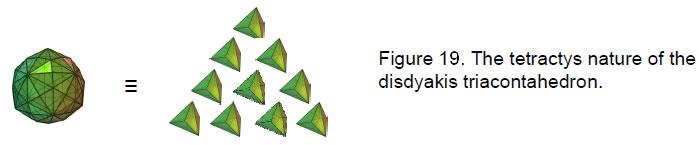
20
solid with the most faces (Fig. 18) and the apotheosis of all polyhedra.12 If this holistic object were symbolized by a tetractys, the Pythagorean model of such systems, Article 2713 showed that the triakis tetrahedron, the Catalan solid with the least number of corners, would be its yod (Fig. 19) because the numbers of vertices, edges and triangles surrounding the axis of the disdyakis triacontahedron are ten times the corresponding numbers for the triakis tetrahedron. Indeed, it was shown in the article14 that the simplest Catalan polyhedron is the 3-dimensional representation of what the author calls the ‘Cosmic Tetractys.’ This is a map of all levels of physical and superphysical reality. The Godname of Kether picks out the triakis tetrahedron from the family of Platonic solids, Archimedean and Catalan polyhedra because it is the 21st polyhedron and 21 is the number value of EHYEH (see the table in reference 1). The Godname EL of Chesed with number value 31 picks out the disdyakis triacontahedron because it is the 31st polyhedron in this family. EL also defines its shape because it is created from 31 vertices and their 31 mirror images and because there are 32 vertices forming the golden rhombic faces of the underlying rhombic triacontahedron, where 32 is the 31st integer after 1. 496 yods belong to the last (6+6) polygons in the inner Tree of Life whose 62 corners unshared with its outer form are the counterparts of the 62 vertices of the disdyakis triacontahedron. 496 is the sum of the first 31 integers. This shows how EL prescribes the 496 roots of the gauge symmetry group E8×E8 of heterotic superstrings. They are symbolized by the 496 yods in the 12 polygons with 62 corners, where 62 is the 31st even integer. Truly, the disdyakis triacontahedron embodies the meaning of EL: ‘God.’
References
1 The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). The table below gives their number values obtained by the practice of gematria, wherein each letter of a word has a number assigned to it, giving a number value to the word that is the sum of the values of its letters. Numbers in the table are written in boldface throughout the text.
Angels
Chakra2 Phillips, Stephen M. Article 25: ”The 33 Vertex Sheets of the Disdyakis Triacontahedron Signify the 33 Tree Levels of Ten Overlapping Trees of Life,” (WEB, PDF), Table 1, p. 11.
3 Phillips, Stephen M. Article 26: “How the Seven Musical Scales Relate to the Disdyakis Triacontahedron,” (WEB, PDF), p. 39.
5 Phillips, Stephen M. Article 27: “How the Disdyakis Triacontahedron Embodies the Structural Parameter
21
1680 of the E8×E8 Heterotic Superstring,” (WEB, PDF), p. 6.
6 Proof: The seven separate polygons have 48 edges. When constructed from tetractyses, the latter have 48 edges that join their 48 corners to the centres of the polygons, making a total of 96 edges of 48 sectors. When enfolded, seven edges of these polygons merge into their shared edge. Two edges of a tetractys in the hexagon become the sides of the triangle. Number of edges in the 7 enfolded polygons = 96 – 6 – 2 = 88. The triangle has 3 internal edges of its 3 tetractyses. Number of edges of the last 6 polygons = 88 – 3 = 85.
8 Besant, Annie, and Leadbeater, C.W. Occult Chemistry, Theosophical Publishing House, Adyar, Chennai, India, 1951.
9 Phillips, Stephen M. Article 19: “I Ching and the Eight-fold Way,” (WEB, PDF).
10 Proof: Let N = a0 + a1e1 + ... + a7e7. Then N-1 = N*/││N││2 and ││N*││= ││N││, so that ││N-1││=
││N*││/││N││2 = ││N││-1. Therefore, (N-1)-1 = (N-1)*/││N-1││2 = [(N*)*/││N││2]×││N││2 = N.11 Phillips, Stephen M. Article 15: “The Mathematical Connection Between Superstrings and Their Micro-psi Description: a Pointer Towards M-theory,” (WEB, PDF), pp. 8-12.
12 For other examples of seven-fold systems, see ref. 9.
22