| << Previous 1... 29 30 [31] 32 33 ...81 Next >> |
#31 Arithmetic & geometric embodiment of the superstring structural parameter 5040 in sacred geometries
Outer Tree of Life

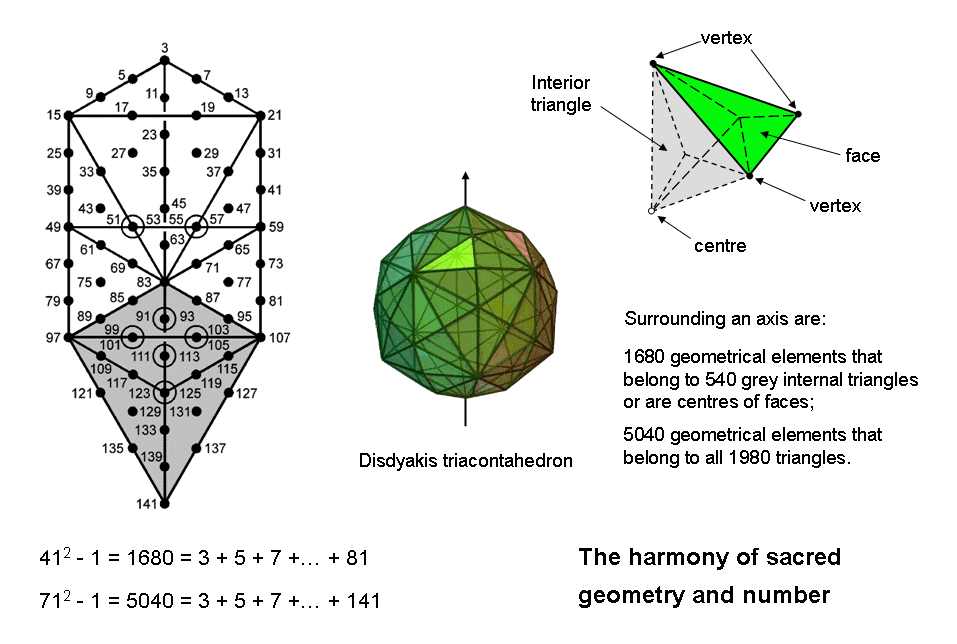
As 5040 = 3×1680, the number 5040 is the number of 1st-order spirillae in the three major whorls of the UPA. That is why it should be regarded as a structural parameter of the E8×E8 heterotic superstring that is a constituent of up and down quarks. As discussed in #15 of Wonders of superstrings, 5040 is the sum of the first 70 odd integers after 1 (3, 5, 7, ... 141) after 1 that can be assigned to the 70 yods in a Tree of Life whose 16 triangles are tetractyses. The sum of the first 40 odd integers after 1 (3, 5, 7, ... 81) that can be assigned to the 40 yods outside the grey Lower Face is 1680 — the number of 1st-order spirillae in a whorl. The sum of the next 30 odd integers (83, 85, 87, ... 141) that can be assigned to the 30 yods in the Lower Face is 3360 = 2×1680.
Disdyakis triacontahedron
Suppose that the 120 triangular faces of the disdyakis
triacontahedron are divided into their 360 sectors. Then suppose that its 62 vertices and the
centres of its faces are joined to its centre. The former process creates 180 internal triangles and the latter
generates (120×3=360) internal triangles. Finally, suppose that these 540 internal triangles are divided into their
3×540=1620) sectors. The table below lists the numbers of corners, sides & triangles in the faces and interior
that surround an axis passing through two diametrically opposite vertices of the disdyakis triacontahedron, which
has 62 vertices, 180 edges & 120 faces:
Geometrical composition of the disdyakis triacontahedron
|
Corners |
Sides | Triangles | Total | |
| Faces | 60 vertices | 180 edges | 360 sectors | |
| 120 centres | 120×3 = 360 | |||
| Subtotal | 180 | 540 | 360 | 1080 |
| Interior | 180 | 60 (vertices-centre) | 180×3 = 540 | 1320 |
| 180×3 = 540 | ||||
| 360 | 120 (centres-centre) | 360×3 = 1080 | 2640 | |
| 360×3 = 1080 | ||||
| Subtotal | 540 | 1800 | 1620 | 3960 |
| Total | 720 | 2340 | 1980 | 5040 |
We see that 5040 corners, sides & triangles surround its axis. Every geometrical element corresponds to a
1st-order spirillae in a major whorl. It was pointed out in #1 of Superstrings as sacred
geometry/Disdyakis triacontahedron that, when the faces are regarded as single triangles
and only the vertices are joined to its centre, 1680 geometrical elements surround the axis. When the faces are
divided into their sectors, this is the number of internal geometrical elements, vertices, edges & centres
of faces. They correspond to the 1680 1st-order spirillae in the first major whorl and to the sum of the first
40 odd integers after 1 outside the Lower Face of the Tree of Life. This means that, when the face centres are
joined to the centre of the disdyakis triacontahedron, the additional 3360 (=2×1680) elements consist of 720
sides & triangles in the faces and 2640 elements in its interior, 1680 elements being in each half of the
polyhedron. They correspond to the 1680 1st-order spirillae in the second major whorl and to the 1680 1st-order
spirillae in the third major whorl, as well as to the sum of the next 30 odd integers in the Lower Face of the
Tree of Life. A beautiful harmony between number and geometry is revealed by comparing the sacred geometries of
the Tree of Life and its polyhedral counterpart — the disdyakis triacontahedron.
We saw in #27 that the number 720 is embodied in the seven separate Type B polygons of the inner Tree of Life as the 720 yods surrounding their centres, in the decagon with 2nd-order tetractyses as sectors as the 720 yods surrounding its centre, in the five Platonic solids as the 720 hexagonal yods in their 50 faces and in the disdyakis triacontahedron as the 720 corners & sides in its faces when they are Type A triangles. When its vertices and face-centres are joined to its centre, there are 720 corners of triangles surrounding an axis of this Catalan solid.
Dodecagon
The dodecagon is the last of the regular polygons of the inner Tree of Life.
The Type B dodecagon shown below has 181 yods,* that is, 168 red yods other than its black
corners and centre. The next higher-order dodecagon is the Type C dodecagon, in which 504 yods surround its centre.
It is composed of the same 168 red yods and has 336 extra blue yods surrounding its centre.
The 10 Type C dodecagons that are enfolded in the inner form of 10 overlapping Trees of Life has 5040 yods
surrounding their centres, of which
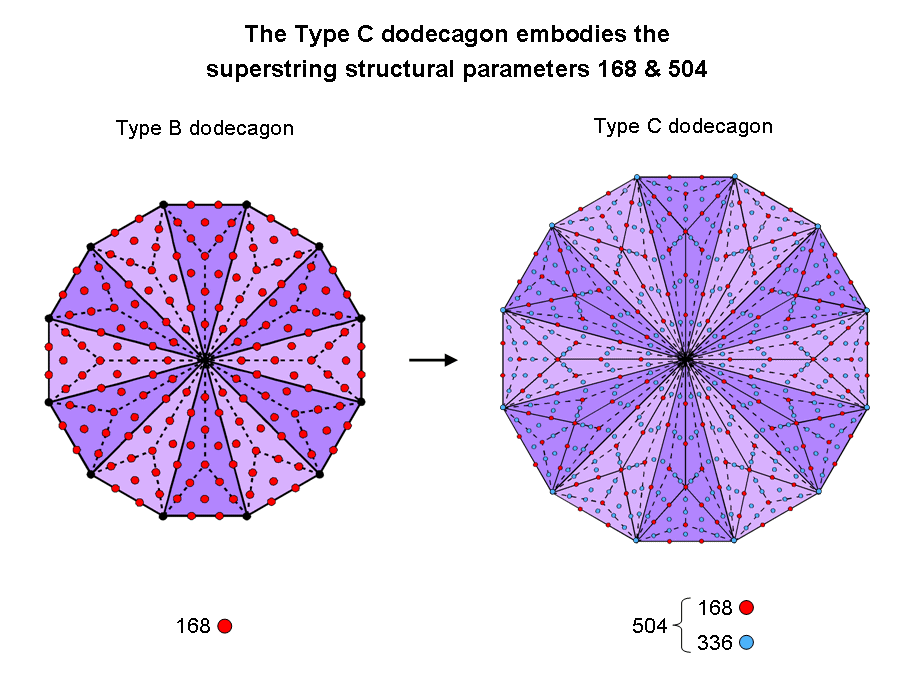
1680 yods belong to their Type B version, leaving 3360 (=2×1680) yods. This 1680:2×1680 division of yods has its arithmetic counterpart in the sums of the first 40 odd integers after 1 assigned to yods outside the Lower Face of the Tree of Life and the next 30 odd integers assigned to yods in the latter. It manifests in the disdyakis triacontahedron as the 1680 geometrical element surrounding its axis other than those in faces that are unshared with its interior and as the 1680 geometrical elements added to each half of the polyhedron by joining the 120 face-centres to its centre and by dividing into their sectors the 360 internal triangles thereby generated.
The three major whorls of the UPA are the micro-physical manifestation of the Supernal Triad of Kether, Chokmah & Binah and the seven minor whorls are the manifestation of the seven Sephiroth of Construction. The 1:2 (×1680) division in the sacred geometrical representation of the three major whorls reflects the pattern of the seed source of the Tree of Life — Kether — and the pair of opposite cosmic polarities — Chokmah & Binah — that emerges from this starting point. The counterparts of the latter in the disdyakis triacontahedron are its two halves, one the mirror image of the other, whose forms are completed when all possible triangles in its faces and interior are divided into their sectors.
According to the table shown above, the number of corners of the 1980 triangles that surround an axis of the disdyakis triacontahedron = 720 = 6! = 1×2×3×4×5×6. It includes 120 face-centres, where 120 = 5! = 1×2×3×4×5. The total number of geometrical elements that surround the axis = 5040 = 7! = 1×2×3×4×5×6×7. The fact that the number of 1st-order spirillae in the three major whorls is 7!, i.e., the number of permutations of seven objects, will prove to have great significance in the M-theory explanation of the 10 whorls of the UPA, perhaps in the context of the seven unit imaginary octonions e1-e7 because there are (7! =5040) possible octonions O of the form:
O = Ae1 + Be2 + Ce3 + De4 + Ee5 + Fe6 + Ge7,
generated by selecting the numbers A-G in all possible ways from any given set of numbers (a1-a7). There is further discussion in #21 at Wonders of sacred geometry/Superstrings about the 5040 geometrical elements in the disdyakis triacontahedron that surround an axis joining two diametrically opposite vertices.
* A Type B n-gon has (15n+1) yods, so that a Type B dodecagon (n=12) has 181 yods. A Type C n-gon has (42n+1) yods, so that a Type C dodecagon (n=12) has 505 yods.
| << Previous 1... 29 30 [31] 32 33 ...81 Next >> |