| << Previous 1... 25 26 [27] 28 29 ...81 Next >> |
#27 Correspondence between the inner Tree of Life, the decagon, the five Platonic solids & the disdyakis triacontahedron

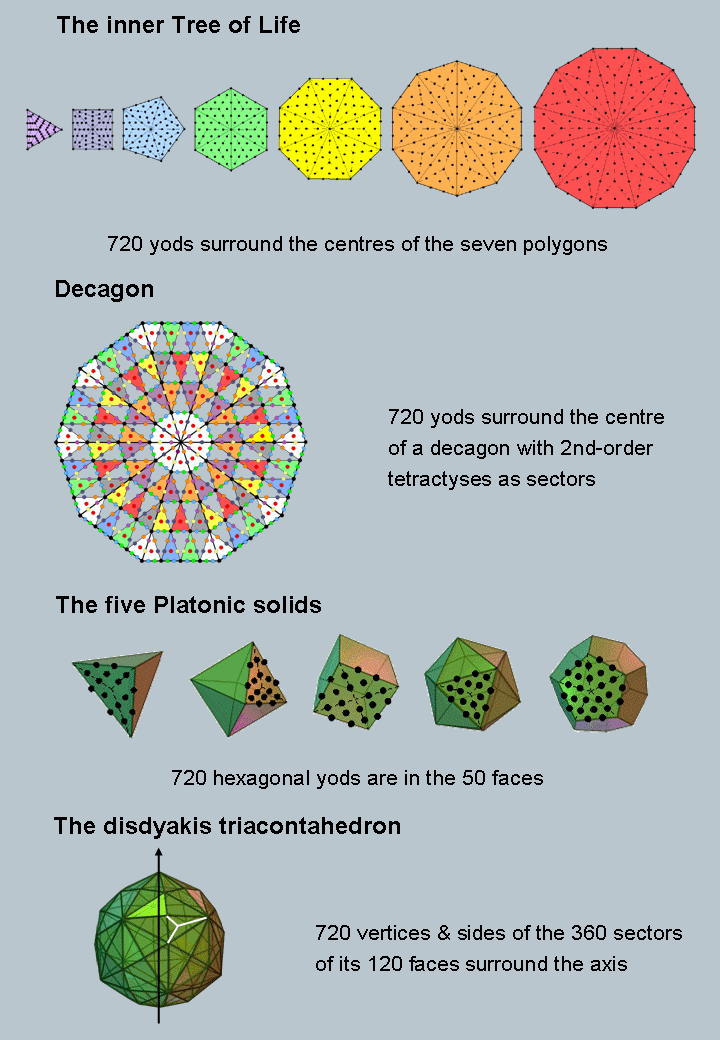
The inner Tree of Life
The number of yods in an n-gon with Type A triangles
as its n sectors = 15n + 1, where "1" denotes its centre. The seven types of separate polygons
making up the inner Tree of Life have 48 sectors with (Σ15n = 15Σn =
15×48 = 720) yods surrounding their centres.
Decagon
A 2nd-order tetractys (see here) has 85 yods. Thirteen yods line each side. When an n-gon is divided
into its n sectors and the latter turned into 2nd-order tetractyses, there are (85−13=72) yods
per sector surrounding the centre of the n-gon. (72×10=720) yods surround the centre of a
decagon with ten sectors.
Five Platonic solids
Imagine that the 50 faces of the
five Platonic solids are divided into their sectors and that each sector is then turned into a tetractys. The table
here indicates that there are 720 hexagonal yods in their faces.
Disdyakis triacontahedron
The disdyakis triacontahedron is the outer form of
the Polyhedral Tree of Life (see here). Sixty vertices, 180 edges and 120 triangular faces surround an
axis (indicated in the diagram opposite by a vertical arrow) that passes through any two diametrically opposite
vertices. Suppose that each face is divided into its three sectors, i.e., it is considered as a Type A triangle.
This creates 120 new corners of sectors and (3×120=360=36×10) new sides (shown in the diagram
by the straight, white lines in a representative face). The total number of corners & sides surrounding the
axis = 60 + 120 + 180 + 360 = 720.
The number 720 is a structural parameter of these sacred geometries. Notice that, as 720 = 144×5 = 122×5, the average number of hexagonal yods in the faces of the five Platonic solids = 122, where 12 is the number of corners of the dodecagon, the last regular polygon in the inner Tree of Life and the tenth type of polygon, counting from the simplest one — the triangle. This is how the Decad (10) determines the average number of hexagonal yods in the faces of the Platonic solids. The average number of hexagonal yods in half a Platonic solid = 144/2 = 72, which is the 36th even integer, where 36 is the number value of ELOHA, the Godname of Geburah, the sixth Sephirah of Construction, counting from Malkuth. This Godname also prescribes the 360 (=36×10) corners & sides in each half of the disdyakis triacontahedron that surround an axis. Notice that 36 = 62 and 720 = 1×2×3×4×5×6.
| << Previous 1... 25 26 [27] 28 29 ...81 Next >> |