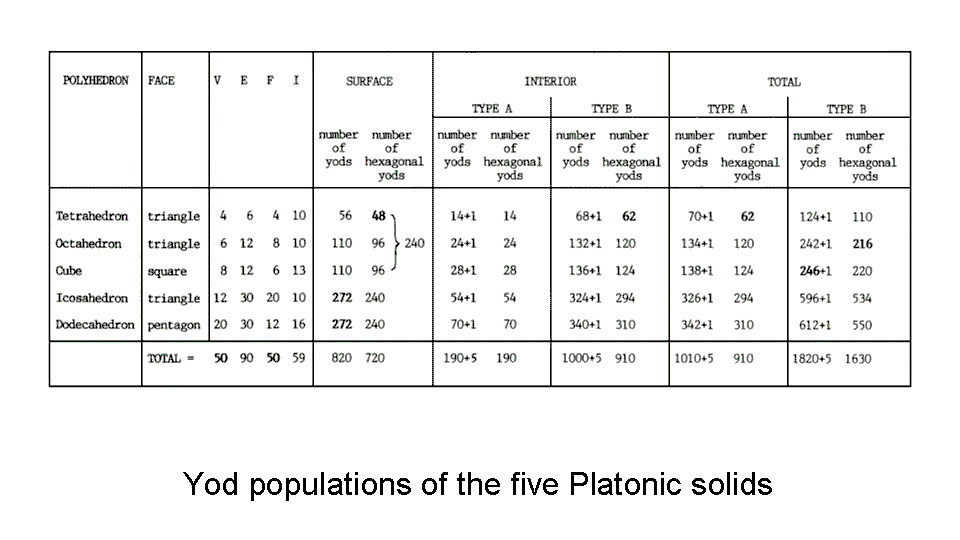
The table lists the numbers of vertices (V), edges (E), faces (F) & yods (I) inside each face of the Platonic solids. Also listed are the numbers of yods (including hexagonal yods) in their surfaces and the number of yods (including hexagonal yods) in their interiors. As an internal triangle can be regarded as either a tetractys (let us call such an interior "Type A") or as having three sectors that are tetractyses (let us call it "Type B"), there are two cases to consider. The first four Platonic solids have 548 yods in their 38 faces. The average number of yods needed to construct their faces = 548/4 = 137. This is the number that is well-known in physics because it determines the fine-structure constant α. The total number of yods in the first four Platonic solids is 672. The average number of yods needed to build their faces and interiors = 672/4 = 168. This is remarkable because 168 is the Mundane Chakra of Malkuth and the average number of turns in a half-revolution of a whorl of the superstring making up the quarks in protons and neutrons inside atomic nuclei, as remote-viewed by Annie Besant & C.W. Leadbeater (see Occult Chemistry). Hence, the surface and volume of the first four Platonic solids associated with the Elements Fire, Air, Water & Earth embody the numbers determining the fine-structure constant and the winding number of the E₈×E₈ heterotic superstring! The latter is discussed in detail here. As explained in Superstrings as sacred geometry/Platonic solids, their faces also determine the root composition of the gauge symmetry group whose gauge fields determine the unified force between superstrings.

According to the table, the faces of the five Platonic solids with tetractyses as their sectors have 820 yods. This is the sum of the squares of the integers 1, 3, 9 & 27, the first four members of a geometric series that mark out one side of Plato's Lambda, the strip of the material of the World Soul from which, according to Plato's Timaeus, God fashioned the celestial sphere (see here):

 1² + 3² + 9² + 27² = 820.

The average number of yods needed to construct their faces = 820/5 = 164 = 3² + 5² + 7² + 9². This illustrates the Tetrad Principle formulated in Article 1, whereby properties of holistic systems are quantified by either the fourth of a class of mathematical object or the sum of the first four members of such a class. In this case, 164 is the squares of the first four odd integers after 1. The number of corners of their 180 tetractyses = 100 = 1³ + 2³ + 3³ + 4³. The average number of corners = 100/5 = 20 = 2 + 4 + 6 + 8. The number of hexagonal yods = 720 = 30×24 = 1×2×3×4(1² + 2² + 3² + 4²). The average number of hexagonal yods = 720/5 = 144 = 9×16 = 9×4² = 9(1 + 3 + 5 + 7) = 9 + 27 + 45 + 63

        1⁰     2⁰     3⁰    4⁰

        1¹     2¹     3¹    4¹
=
        1²     2²     3²    4²

        1³     2³     3³    4³  .

The dodecahedron with Type B interior triangles has 550 hexagonal yods. This number is defined by the Decad (10) because 550 = 55×10, where 55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10. It is a basic parameter of all holistic systems. Maps of reality discusses how the number 550 is found in other sacred geometries to be a measure of the spiritual cosmos.

<< Previous    1...   14  15  [16]  17  18  ...19    Next >>

Home