Home

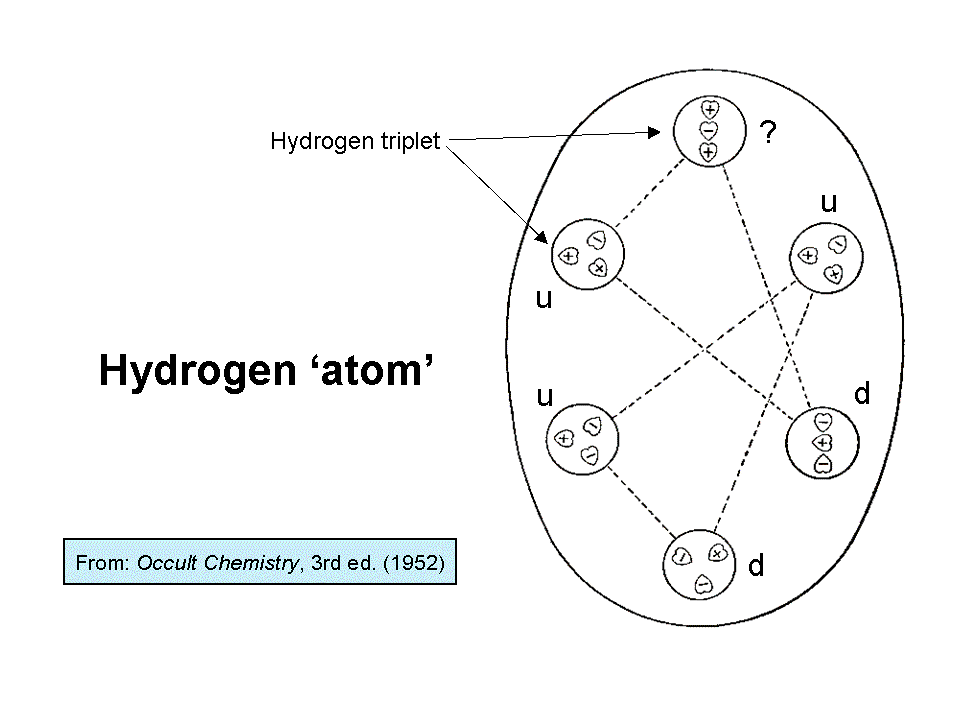
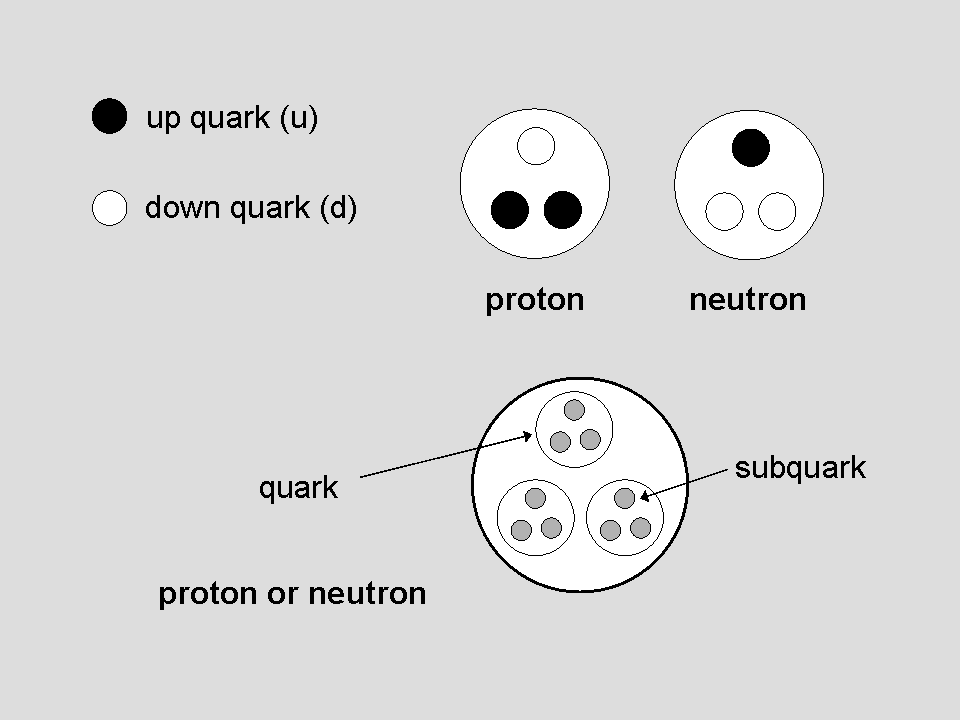
Let us compare the quark model of a proton and neutron with the micro-psi description of the hydrogen MPA given by Besant & Leadbeater. Two interpenetrating triangles ("hydrogen triangles") are enclosed by an egg-shaped wall, or, rather, a transparent surface, as though they were inside an oval hole or cavity in some fluid. At the corners of each triangle are spheres that contain groups of three UPAs, arranged as triangles ("H3 triplets") in the lower hydrogen triangle and as one H3 group and two linear arrays ("H3′ triplets") in the upper hydrogen triangle. In the first edition of Occult Chemistry, the linear triplets are shown in both triangles. The third edition states that this form was rare because it was not observed when Leadbeater re-examined hydrogen in 1932. Presumably, he meant only that he rarely observed it because it is unlikely that a form of hydrogen that rarely occurs naturally would have been described long before its more abundant form was noticed. Hydrogen triplets were called either positive or negative. Besant & Leadbeater did not explain what they meant by this, although, at the beginning of the investigations, it seems to have been based upon whether an object contained more (+) UPAs than (−) UPAs. They did, however, indicate the difference in their diagrams by depicting positive triplets (as they did for all groups of UPAs they deemed positive) with their heart-shaped UPAs pointing outward from the centre of the group and by depicting negative triplets (and all negative groups in general) with their UPAs pointing inwards towards their centres. The upper hydrogen triangle contains one positive H3 triplet, one negative H3′ triplet and one H3′ triplet of indeterminate polarity because, breaking their own convention, it depicts three UPAs pointing in the same downward direction. The lower hydrogen triangle consists of two positive H3 triplets and one negative H3 triplet. Notice that one of the former has two (+) UPAs and one (−) UPA and the other has two (−) and one (+) UPA. Here is an indication that the polarity of triplets (and, in general, groups of more UPAs) was not determined by the net number of (+) or (−) UPAs.

Comparison with the composition of the proton in terms of two positively charged up quarks and one negatively charged down quark suggests that the lower hydrogen triangle with two positive triplets and one negative triplet is a proton. This is the nucleus of a hydrogen atom and it should be present in the hydrogen MPA. The natural inference is that a positive triplet is a u quark and a negative triplet is a d quark. This implies that the positive H3 triplet in the upper hydrogen triangle is an up quark and the negative H3′ triplet is a down quark. The nature of the other H3′ triplet cannot be deduced because its depiction in the third edition of Occult Chemistry is ambiguous (hence the question mark next to it added by the author). It is either an up or down quark, so this hydrogen triangle is either a proton or neutron. The former possibility is ruled out because the hydrogen MPA was reported to be stable, whereas a diproton (a pair of protons strongly interacting with each other) is known to be unstable. The upper hydrogen triangle must therefore be a neutron, which can form a stable bound state with the proton. This would be possible if, in the stage prior to their observation, the two protons in a hydrogen molecule had overcome their mutual electrostatic repulsion due to their similar electric charges and have collided with each other, causing one proton to change into a neutron which then became bound to the proton, creating a stable deuteron. This is a nuclear reaction that is well-known to nuclear physicists:

¹H₁ + ¹H₁ → ¹H₂ + π⁺.

An observation that is consistent with the hydrogen MPA being a deuteron formed prior to observation is that "each of the three groups making one half of Hydrogen are linked to each other across space by lines of attraction." This would be the nuclear force binding the proton and neutron together in a deuteron. The observed overlap between the two hydrogen triangles further supports this interpretation of the hydrogen MPA because the nuclear force is a short-range force, and so it would not have been noticed unless the proton and neutron had been sufficiently close for this attractive force to act between them. Other than the irresolvable ambiguity in the quark identity of the H3′ triplet in the upper hydrogen triangle, every aspect of the hydrogen MPA is explained. It has the vital implication that the UPA is the basic constituent of up and down quarks. In other words, quarks are not fundamental particles, as the Standard Model of particle physics assumes. This is a revolutionary implication of the micro-psi observations of Besant & Leadbeater.

A hypothesis about MPAs

If the hydrogen MPA was formed prior to its observation from two protons, i.e., from the nuclei of the two hydrogen atoms in a molecule of this element, perhaps the MPA of every element was formed from two of its atomic nuclei? Let us hypothesize this and explore its predictions for the populations of MPAs, given that UPAs must be subquarks if the interpretation of the hydrogen MPA given above is correct. As protons and neutrons contain three quarks, each with three subquarks, and a nucleus of mass number A contains A protons & neutrons, i.e., 9A subquarks, the number of UPAs predicted to be in an MPA formed from nuclei of two nuclides of an element with mass numbers A₁ and A₂  = 9(A₁ + A₂). If the nuclides are identical and have a mass number A, the number of UPAs in the MPA formed from two similar nuclei = 18A. The number weight, which was defined by Besant & Leadbeater as:

Number weight = number of UPAs in MPA/18,

is predicted to be equal to the mass number A. As most elements have stable nuclides with mass numbers within one or two units range of their atomic weights, this would explain why Besant & Leadbeater found their calculated number weight for each element to be approximately equal to its atomic weight. It never made sense for them to believe that this could be an exact relation, for an atomic weight is now defined as the ratio of the average mass of an atom of an element to 1/12 of the mass of an atom of C-12, which is a stable nuclide of the element carbon. In other words, unlike a number weight, the 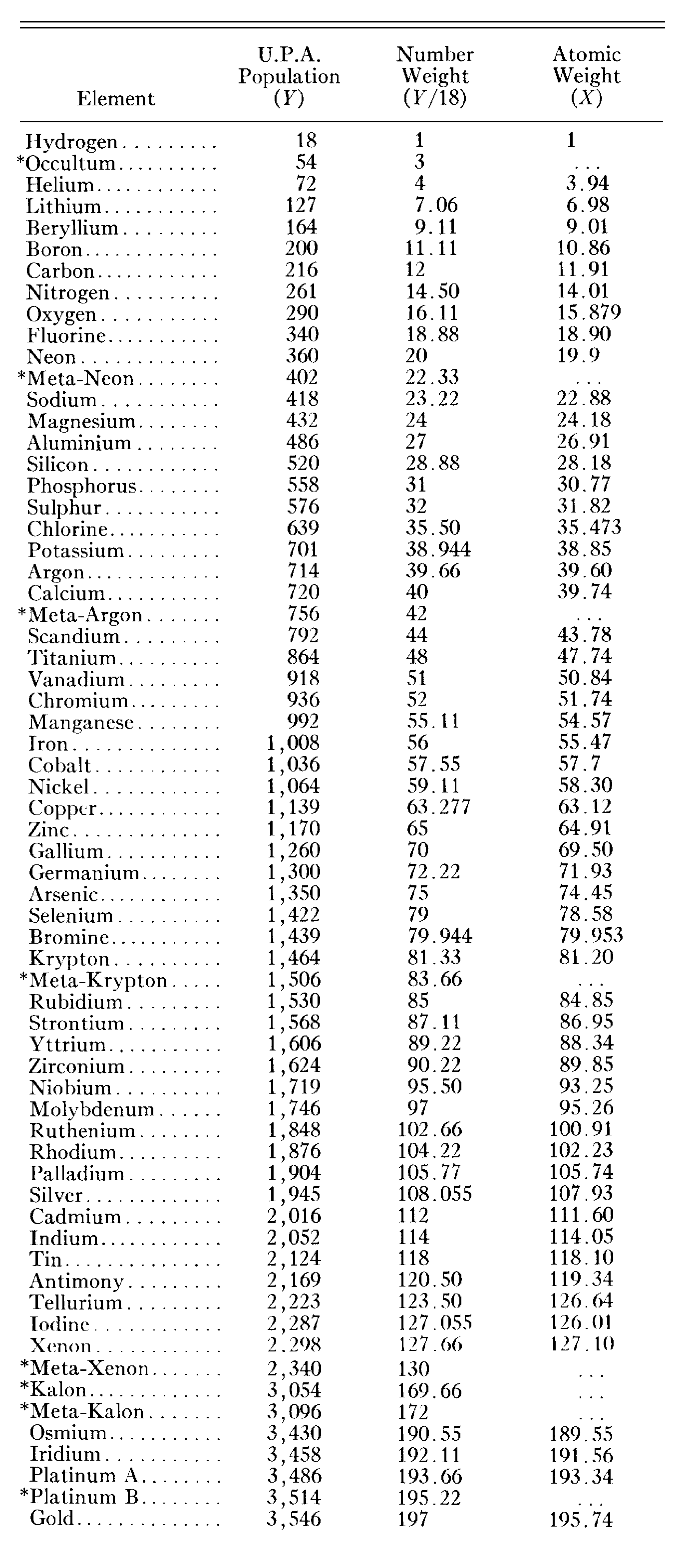atomic weight refers not to a specific isotope but to all nuclides in a given sample of the element. Despite this, it was accurate in practice as a means of identifying which element corresponded to a given MPA. As many as 39 of the complete sample of 111 MPAs have UPA populations that are exactly eighteen times the mass numbers of (usually) the most abundant nuclide of their corresponding element. If Besant & Leadbeater had fabricated UPA populations so that their number weights would be approximately equal to atomic weights, thereby creating an impressive correlation with chemistry, it is highly improbable that a fraction of these populations as large as one-third would by chance create number weights that were exactly equal to the mass number of a stable nuclide. They could not, of course, have concocted populations based upon mass numbers because the notion of mass number became established only after 1932, when James Chadwick discovered the neutron, that is, 24 years after Occult Chemistry was published.

Some sceptics may suggest that Besant & Leadbeater devised UPA populations so that they would generate number weights that were equal not to atomic weights but to their values rounded off to the nearest integer. In the first edition of Occult Chemistry, published in 1908, they compared their calculated number weights for 65 MPAs with the values recognized then of atomic weights, mostly listed in the so-called "International List" of 1905, given in Erdmann's "Lehrbusch der Unorganischen Chemie" (see table). In contradiction to what sceptics might suspect, namely, that they made up UPA populations so as to procure agreement with the latest list of atomic weights, Besant & Leadbeater states: "These weights differ from those hitherto accepted, and are generally lighter than those given in earlier textbooks. It is interesting to note that our counting endorses the earlier numbers, for the most part, and we must wait to see if later observations will endorse the last results of orthodox chemistry, or confirm ours." (Occult Chemistry, 1st ed., p. 21, the author's italics). What hoaxers would publish fabricated data that they admitted fitted earlier scientific data rather than the latest (and therefore most reliable) lists of atomic weight?! Except for hydrogen, none of these atomic weights (listed opposite), which presumably, because they mentioned it, Besant & Leadbeater referred to when they compared number weights with them, is an integer, let alone one that is an integer multiple of 18. It means that these particular scientifically determined numbers gave them no reason to make UPA populations either multiples of 18 or such that the calculated number weights would be whole numbers. Yet such multiples occur in a significant fraction (about one-third) of the 111 MPAs that were recorded. Let us suppose that, intent on making up the data, they had decided for some reason that the hydrogen MPA should have 18 UPAs and that — in order to procure the best agreements between their concocted number weights and scientific atomic weights available then — they fabricated populations by making them those integers that are nearest to the fractional value of the product of 18 and the relevant atomic weight. It is extremely improbable that such a large proportion of fabricated populations would have turned out by chance to be exact, integer multiples of 18. Indeed, it was pointed out earlier that the relationship N = 18X, where N is the UPA population and X is the atomic weight listed in the International List of 1905, gives a very poor fit to the micro-psi data that had accumulated by 1908, there being less than one chance in ten thousand that it could have been fabricated in this way. This refutes the suggestion made by sceptics that Besant & Leadbeater used this particular list to concoct UPA populations that were approximately proportional to atomic weights. They did, of course, state that they knew of other earlier tables, which they said gave better agreement. However, even supposing that they had used them and then discovered to their dismay that later scientific measurements of atomic weights gave poorer support to their concocted number weights, this scenario still does not account for why as many as one-third of these numbers are integers, for chemists knew then that nearly all measured atomic weights were not whole numbers, so they had no motive to create such a large fraction of UPA populations with integer number weights. As educated Victorians, Besant & Leadbeater were probably aware of "Prout's hypothesis," made in 1815-1816 by the English chemist William Prout, in which he proposed that the atoms of the elements were groupings of various numbers of hydrogen atoms. But it had been disproved by 1832 by careful measurements of many fractional atomic weights, such as the value 35.45 for chlorine. So, if they were aware of this, the two Theosophists would not have been motivated to fabricate observations that supported a long-discredited idea. Although Prout's idea turned out to be near the truth, it certainly did not influence the two Theosophists, for hydrogen MPAs do not appear in any of the MPAs that they published, apart from that of helium. On the other hand, if they had been unaware that Prout's hypothesis was not supported by measured atomic weights and if they had wanted to create MPAs whose UPA populations were integer multiples of 18 so as to provide support for it, it would have been far easier to fabricate MPAs made up of pairs of hydrogen triangles — hydrogen MPAs — than to invent dozens of types of groups of UPAs in such numbers as to make as near as possible the UPA population an exact multiple of 18. Indeed, the very absence of hydrogen MPAs in the MPAs of elements and the presence, instead, of many types of particles other than hydrogen triangles amounts to irrefutable evidence that MPAs are not even atomic nuclei, let alone fabricated representations of atoms.

What, therefore, are they? It was proposed in the author's books that MPAs are formed prior to anything becoming visible in the field of view of the remote viewer. The act of preparation for observation psychokinetically injects energy into the space around selected atoms that heats up the Higgs field, making it no longer superconducting. This property is believed by advocates of the string model of quark confinement to squeeze the colour flux lines emanating from quarks into narrow flux tubes through the Meissner Effect. With the Higgs field now behaving as a normal conductor, the confinement mechanism for quarks no longer operates because the strings can no longer exist as vortices and quarks become free. The protons and neutrons in pairs of atomic nuclei disintegrate into quarks and subquarks, which, too, are normally confined by the Meissner Effect because they are bound by strings inside quarks as well. But the Higgs field then cools below its critical temperature, returning to the superconducting state and trapping quarks and subquarks in new, exotic string configurations, many of which have yet to be discovered in the high-energy physics laboratory. Far from being a feature that contradicts nuclear physics if MPAs were atomic nuclei, the variety of bound states recorded in them is one that should be expected, according to this radical scenario for their formation, in which a pair of nuclei briefly turn into a quark-gluon plasma before condensing into multi-quark bound states.

As one cannot be certain a priori which nuclide formed a given MPA (there are exceptions to this which will be discussed later), a choice has to be made of the particular one for a given element that Besant & Leadbeater most likely examined. Three criteria determine this choice:

1. Abundance. The nuclide of an element with the greatest terrestrial abundance is normally chosen because its atoms are the most likely to have been examined, making the plausible assumption that selection by the remote viewer is a purely random process. If this choice conflicts with criteria 2 and/or 3 stated below, the next most abundant nuclide satisfying all the criteria is chosen.
2. Stability. Unless the element is naturally radioactive, the nuclide must be stable. All choices refer to the ground state of the nuclide.
3. Plausibility of error. The difference: e = N − 18A between the number (N) of UPAs counted in an MPA and the predicted number of subquarks for the nuclide in question represents the total observational error. This accumulated from individual mistakes in counting the numbers of UPAs in different groups and/or from false assumptions that particles that were familiar to Besant & Leadbeater, having been seen in other MPAs, contained exactly the same numbers of UPAs as that which had been counted on earlier occasions. Because the task of counting every one of the possibly thousands of UPAs was too laborious, the investigators counted for all particles that had not been seen earlier but did not bother to do this in the case of familiar groups of UPAs. Instead, they counted these groups and then calculated how many UPAs there were altogether, taking into account the symmetry of the MPA. This procedure introduced a source of systematic error in which any error of counting that occurred during previous examinations of a group or set of groups would be artificially magnified to create a discrepancy that was larger than actual, individual errors of counting. Hence, the magnitude of the predicted net error has to be consistent with the numbers of various, similar structural units, which were not individually counted, otherwise the chosen nuclide is not a plausible candidate for the MPA. For example, a nuclide is not a likely choice if it predicts an error of e = +3 for an MPA that consists of four identical parts, because only one part would have been examined after checking that they were similar, so that any miscounting of UPAs in this particular one would have led to a net error that was a multiple of 4 (this assumes, of course, that the four parts were exactly similar, but it is a safe assumption to make because MPAs were found to be mostly composed of structural components that had been seen earlier in MPAs whose groups of UPAs had all been carefully counted because they had not been observed before).

Criterion 3 does not need to be invoked very often. However, it is as important a factor as criterion 1 in determining the choice of the most likely nuclide. One cannot simply select the most abundant isotope without concern for whether it predicts a discrepancy that is explainable in terms of random errors. This may be the most likely one, statistically speaking, for a given element. But it is not plausible if the magnitude of its predicted error is incompatible with the symmetry of the MPA and the numbers of the similar groups of UPAs within it. Nor is it plausible that the most abundant isotope would always have been the one that formed every one of the 111 MPAs that were recorded. Where a choice creates conflict between criteria 1 & 3, the latter trumps the former. If it does, the next most abundant isotope that satisfies criterion 3 must be chosen.

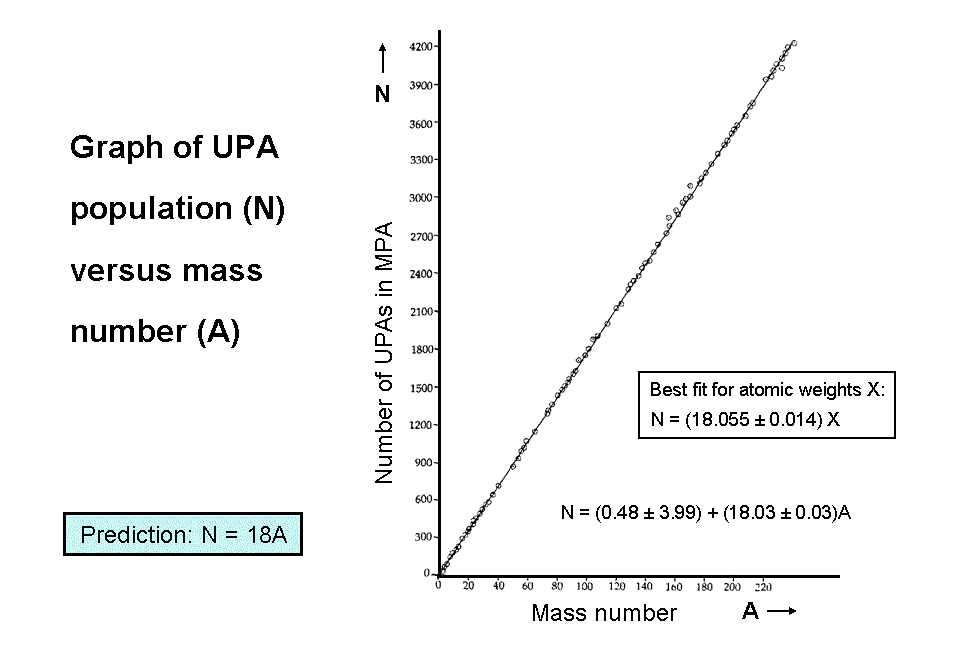
When the UPA populations determined by Besant & Leadbeater are plotted against the mass numbers of the most plausible nuclides that formed the MPAs, as determined according to the three criteria listed above, they are found to be best fitted by the straight line:

N = (0.48 ± 3.99) + (18.03 ± 0.03)A.

It confirms the theoretical prediction N = 18A at the 95% significance level. The fit, however, for MPAs of 65 elements and isotopes with the atomic weights X from the 1908 International List is very bad:

N = (18.055 ± 0.014)X.

The relation N = 18X deviates from the best fit by almost four standard deviations, making it highly improbable (p<10⁻⁴) that it was used to fit data from this list.

The identification of MPAs of elements with one isotope having 100% terrestrial abundance is free of ambiguity because it is absolutely certain that Besant & Leadbeater would have examined only the single, naturally occurring isotope of these elements. The 23 nuclides with 100% abundance:

 ⁹Be, ¹⁹F, ²³Na, ²⁷Al, ³¹P, ⁴⁵Sc, ⁵⁵Mn, ⁵⁹Co, ⁷⁵As, ⁸⁹Y, ⁹³Nb, ¹⁰³Rh, ¹²⁷I, ¹³³Cs, ¹⁴¹Pr, ¹⁵⁹Tb, ¹⁶⁵Ho, ¹⁶⁹Tm, ¹⁹⁷Au, ²⁰⁹Bi, ²³²Th, ²³¹Pa & ²³⁸U

provide the best fit:

N = (18.042 ± 0.044)A,

the proportionality constant differing from the theoretical value 18 by less than one standard deviation. MPAs of elements with only one stable isotope therefore give strong support to the hypothesis that MPAs are formed from two atomic nuclei of an element.

<< Previous    1...   4  5  [6]  7  8  ...13    Next >>

Home