| << Previous 1... 3 4 [5] 6 7 ...8 Next >> |
An astounding connection between the Platonic solids and the paranormally observed UPA
The first four Platonic solids embody the paranormally-determined superstring structural parameter 1680
It was shown on page 4 that the centres of the five Platonic solids are surrounded by 1680 yods other than non-polyhedral corners of tetractyses making up the interiors and faces of these polyhedra. The possibility that the superstring structural parameter 1680 — the number of turns in each helical whorl of the UPA — arises by chance here was refuted by pointing out that the number of yods lining sides of tetractyses in the five solids equals the yod population of the inner form of the Tree of Life — a property that would also have to be coincidental if the number 1680 had arisen by chance. Such a circumstance is too implausible to be credible. Another amazing way in which this number manifests — this time in the first four Platonic solids — will be discussed next.

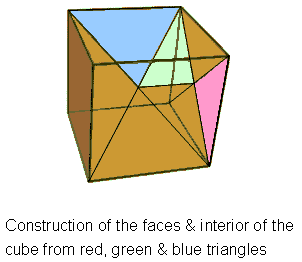
Consider a Platonic solid with V vertices, E edges & F faces that are regular n-gons. The cube in the diagram above is an example of how the faces and interiors of Platonic solids can be constructed from triangles. Dividing their faces into their nF sectors (the red triangle in the diagram is such a sector) generates F corners, so that the Platonic solid has (V+F) corners & (E+nF) sides of nF triangles in its faces. Joining its V vertices to its centre creates V sides of E internal triangles (the blue triangle is an example). When the latter are Type A, there are also E corners & 3E sides of 3E sectors. Joining the F centres of faces to the centre of the solid generates F internal sides & nF internal triangles (the light green triangle is an example). When these triangles are Type A, nF corners & 3nF sides of 3nF sectors are added. The numbers of geometrical elements surrounding its centre are tabulated below:
| Corners | Sides | Triangles | Total | |
| Faces: | V + F | E + nF | nF | 2 + 2E + 2nF |
| Interior: | E + nF | V + F + 3E + 3nF | 3E + 3nF | 2 + 8E + 7nF |
| Total: | 2 + 2E + nF | 2 + 5E + 4nF | 3E + 4nF | 4 + 10E + 9nF |
(Euler's polyhedral formula for a simply-connected polyhedron:
V – E + F = 2
has been used to simplify the expressions). The number "2" in the expression for the geometrical composition of the faces can be interpreted as the two vertices lying on an axis that passes through the centre of the polyhedron. The number "2" in the expression for the composition of the interior denotes the two sides shared by some internal triangles that form this axis. The number "4" in the expression for the total number of geometrical elements denotes the two vertices & two sides surrounding the centre that make up the axis of the Platonic solid. The number of corners, sides & triangles surrounding this axis = 10E + 9nF. For the first four Platonic solids with 60 edges & 38 faces with 120 sectors, the number of geometrical elements that surround their axes = 10×60 + 9×120 = 1680. The dodecahedron with 30 edges & 12 faces with 60 sectors has (10×30 + 9×60 = 840) elements surrounding its axis. This is very remarkable, for the number 1680 is the number of 1st-order spirillae in each whorl of the UPA, whilst the number 840 is the number of 1st-order spirillae in an outer or inner half of a whorl! Indeed, every Platonic solid embodies a superstring structural parameter:
| Platonic solid | Edges (E) | n | Faces (F) | 10E + 9nF |
| Tetrahedron | 6 | 3 | 4 | 168 |
| Octahedron | 12 | 3 | 8 | 336 |
| Cube | 12 | 4 | 6 | 336 |
| Icosahedron | 30 | 3 | 20 | 840 |
| Subtotal = | 60 | - | 38 | 1680 |
| Dodecahedron | 30 | 5 | 12 | 840 |
There are 168 1st-order spirilla in a half-revolution of a whorl, 336 spirillae in a complete revolution, 840 spirillae in the 2½ revolutions making up an inner or outer half of a whorl and 1680 spirillae in the five revolutions of a whorl about the axis of spin of the UPA/subquark superstring. Each half of both the octahedron and its dual — the cube — is composed of 168 geometrical elements that surround their axes. The table indicates that the tetrahedron, octahedron and cube have (168+336+336=840) geometrical elements surrounding their axis, as have both the icosahedron and the dodecahedron. The 840:840 division of 1st-order spirillae in the outer and inner halves of a whorl corresponds to the 840 geometrical elements surrounding the axes of the first three Platonic solids and to the 840 geometrical elements surrounding the axis of the icosahedron. Alternatively, it corresponds to either the 840 geometrical elements surrounding the axes in each half of all four solids or to the 840 elements in their faces and interiors that are created by edges and to the 840 elements in the internal triangles created by sides of sectors. The table below lists the numbers of geometrical elements in their faces & interiors that surround their axes:
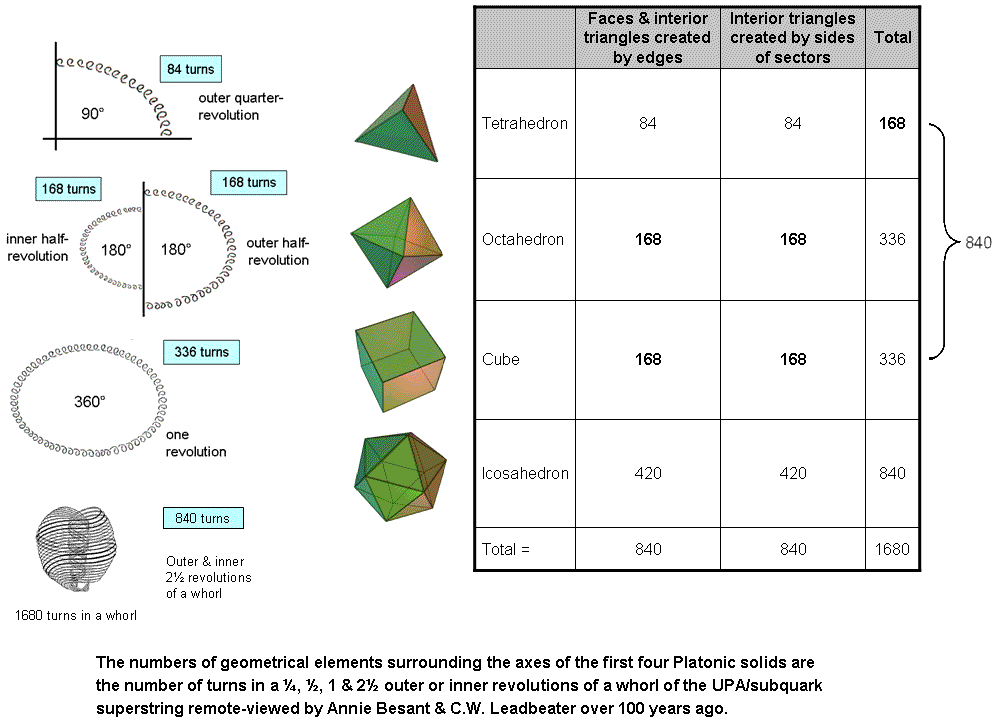
The fact that there are three possible ways of comparing the 840 spirillae in the outer or inner halves of each whorl to the first four Platonic solids — three ways of dividing the number 1680 into two 840s — is very remarkable, and it thoroughly refutes any suggestion that coincidence could be operating here. It is clear that such a possibility is improbable in the extreme! Notice that the tetrahedron embodies the number value of Cholem Yesodoth because 168 geometrical elements surround its axis. The simplest Platonic solid represents the seed that flowers into full expression in the icosahedron and its dual — the dodecahedron — with the appearance of the numbers 840 and 1680. Notice also that the first four Platonic solids have ten times the number of geometrical elements surrounding their axes as the tetrahedron because their faces have ten times as many edges and ten times as many sectors (60 edges compared with six edges & 120 sectors compared with 12 sectors). This means that, when applied to the first four solids, the formula 10E + 9nF used above creates an overall factor of 10. Observe, too, that no single Platonic solid embodies the number 1680. This property appears in an Archimedean or Catalan solid only in the disdyakis triacontahedron (see the last entry in the table here). Surrounding the axes of the tetrahedron, octahedron & cube are, respectively, 168, 336 & 336 geometrical elements, i.e., numbers that correspond to a half, one & one revolution of a whorl. The first three Platonic solids are the counterpart of 2½ revolutions of a whorl and the icosahedron with 840 elements around its axis are the counterpart of another 2½ revolutions. Amazingly, this 3:1 division of Platonic solids corresponds to the splitting of the five revolutions of each whorl into an outer section of 2½ revolutions and an inner, narrower spiral of 2½ revolutions! The five-fold winding of each whorl about the spin axis of the UPA and the distinction between its inner and outer halves are naturally represented in the first four Platonic solids. Like the icosahedron, the axis of the dodecahedron is also surrounded by 840 geometrical elements, and we may represent each whorl of the UPA by the 1680 geometrical elements surrounding the axes of this pair of Platonic solids. The question arises: which solid corresponds to the outer half of a whorl and which to its inner half? As the dual of each other, neither polyhedron is more fundamental than the other in a mathematical sense. However, purely mathematical considerations are insufficient to answer this question and we need to remember that the dodecahedron had a "higher" status for the ancient Greeks, being associated with the superphysical Element Aether, in contrast with the icosahedron, which they associated with the physical Element Water. From an intuitive perspective, the dodecahedron should represent the half of a whorl in the inner core of the UPA and the icosahedron should represent the half of a whorl forming its outer body. Modern science rejects the reasons given by Plato for associating each Element with a regular polyhedron. Nevertheless, that the Platonic solids determine the basic physics of matter remains a sound, mathematical insight, albeit in a more sophisticated and fundamental way than ancient philosophers could have imagined. The first four Platonic solids embody both the dimension 248 of E8 and the paranormally-derived number 1680 — two fundamental, dynamical and structural parameters of the E8×E8 heterotic superstring.
See Article 55 and here for more detailed discussion of these amazing embodiments of superstring structural parameters in the first four Platonic solids.
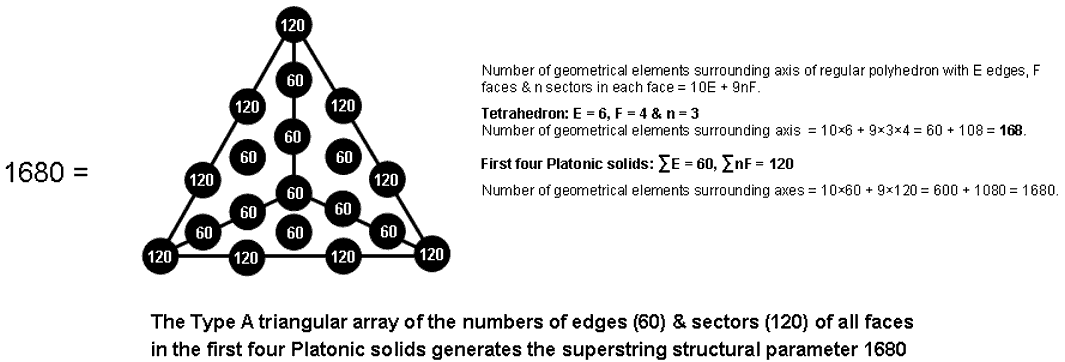
A Type A triangle has nine yods on its sides and 10 yods inside it. Comparing this with the formula 9nF + 10E established above for the number of geometrical elements surrounding a Platonic solid with E edges and F faces, each with n sectors, we see that assigning E to each of the 10 internal yods and nF to the nine boundary yods generates this number. For the first four Platonic solids, ∑E = 60, which is the number of yods surrounding the centre of a 10-sided decagon, and ∑nF = 120, which is the sum of the first 10 odd integers after 1:
| 3 | ||||
| 5 | 7 | |||
| 120 = | 9 | 11 | 13 | |
| 15 | 17 | 19 | 21 . |
Assigning these two numbers determined by the Decad to the 19 yods in a Type A triangle (19 = 10th odd integer) generates the superstring structural parameter 1680. This illustrates the power of the Pythagorean Tetrad and Decad in determining numbers like 1680 that have universal significance because they are defining parameters of holistic systems.
Embodied, therefore, in what the ancient Greeks believed are the shapes of the particles of the Elements Fire, Air, Water & Earth are the very structural parameters 168, 336, 840 & 1680 of each whorl of the UPA as the subquark state of the E8×E8 heterotic superstring. This is one of the most important discoveries discussed in this website that relate sacred geometries to superstring physics and to the micro-psi observation by Besant & Leadbeater of the UPA. It compares with the 1680 geometrical elements that surround an axis of the disdyakis triacontahedron — the outer form of the polyhedral Tree of Life (see here & here) — when its internal triangles are not divided into their sectors and the centres of its faces are not joined to its centre. When they are joined (noting that E = 180, F = 120, n = 3 and nF = 360), the number of geometrical elements surrounding the axis of the disdyakis triacontahedron = 10×180 + 9×360 = 5040. This is just as remarkable, for the number 5040 (=3×1680) is the number of 1st-order spirillae in the three major whorls of the UPA/heterotic superstring. So the construction of the edges of this polyhedron from triangles creates 1680 geometrical elements around its axis, whilst addition of internal triangles, some of whose sides divide its faces into their sectors, requires 2×1680 elements; each element corresponds to a 1st-order spirilla in the three major whorls of the UPA.
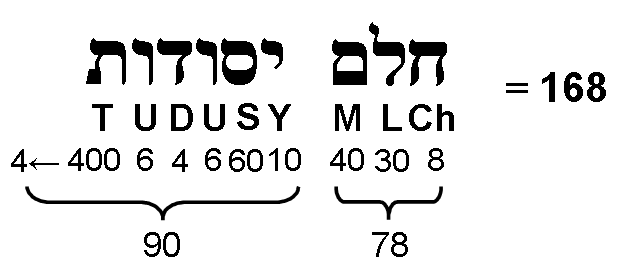
That it is not mere coincidence that there are 1680 geometrical elements surrounding the axes of the first four Platonic solids is confirmed by the facts that (using the formulae given above for the numbers of corners, sides & triangles in a Platonic solid) there are (2×60 + 120 = 240) corners, (5×60 + 4×120 = 780) sides and (3×60 + 4×120 = 660) triangles surrounding the axes of these solids. In other words, (240 + 660 = 900 = 90×10) corners & triangles surround these axes, as well as 780 (=78×10) sides. Once again, the number 78 of Cholem and the number 90 of Yesodoth manifest in the geometrical elements surrounding the axes of the first four Platonic solids. It is highly unlikely that this could happen by chance as well! Rather, their embodiment of the superstring structural parameter 1680 is a powerful example of how the gematria number values of the Sephiroth in the four Kabbalistic Worlds determine the properties of holistic systems like the subquark state of the E8×E8 heterotic superstring — the manifestation of the universal Tree of Life blueprint in the subatomic world.
| << Previous 1... 3 4 [5] 6 7 ...8 Next >> |