| << Previous [1] 2 3 4 5 ...8 Next >> |
The Platonic Solids
|
|
||||
| Tetrahedron Octahedron Cube Icosahedron Dodecahedron | ||||
Consider the faces of the five Platonic solids divided into their triangular sectors. The table below lists the
number of corners, sides and triangles in each solid:
|
Polyhedron |
V |
E |
F |
m |
C |
e |
T |
Total = C + e + T |
|
Tetrahedron |
4 |
6 |
4 |
3 |
8 |
18 |
12 |
38 |
|
Octahedron |
6 |
12 |
8 |
3 |
14 |
36 |
24 |
74 |
|
Cube |
8 |
12 |
6 |
4 |
14 |
36 |
24 |
74 |
|
Icosahedron |
12 |
30 |
20 |
3 |
32 |
90 |
60 |
182 |
|
Subtotal |
30 |
60 |
38 |
– |
68 |
180 |
120 |
368 |
|
Dodecahedron |
20 |
30 |
12 |
5 |
32 |
90 |
60 |
182 |
|
Total = |
50 |
90 |
50 |
– |
100 |
270 |
180 |
550 |
(V = number of vertices, E = number of edges, F = number of faces, m = number of sectors in a face, C = V + F = number of corners of sectors, e = E + mF = number of sides of sectors, T = mF = number of triangles in F faces).
The entries in the upper blue row of the table indicate that the 120 triangular sectors of the 38 faces of the first four Platonic solids have (30+38=68) corners and 180 sides, i.e., 248 corners & sides. This shows how they embody the dimension 248 of the rank-8, exceptional Lie group E8 that is at the heart of superstring theory (see section entitled "Superstring gauge symmetry group" here). The ancient Greeks believed that the tetrahedron, octahedron, cube & icosahedron were the shapes of the particles of, respectively, the elements Fire, Air, Earth & Water. We now see that these Platonic solids do, indeed, represent the properties of physical matter in a fundamental way because the geometrical composition of their faces is expressed by a number that, according to E8×E8 heterotic superstring theory, is the very number of particles transmitting the unified force between superstrings of ordinary matter. Although the historical reason for their association with matter was wrong, the ancient belief that the first four Platonic solids expressed the physics of the universe turned out to be a sound intuition.
There are 368 points, lines & triangles in the faces of the first four Platonic solids. Sixty corners, 180 sides & 120 triangles surround axes passing through pairs of opposite vertices, i.e., 360 (=36×10) geometrical elements. This shows how ELOHA, Godname of Geburah with number value 36, prescribes the first four Platonic solids. Remarkably, the disdyakis triacontahedron (part of the Polyhedral Tree of Life) has 60 vertices, 180 edges & 120 faces surrounding any axis joining pairs of opposite vertices. On average, (360/4=90) geometrical elements surround the axes of the first four Platonic solids. The holistic parameter 90, which appears in the discussion of the Platonic Lambda (see here) manifests in this subset of the complete set of five Platonic solids, which have 90 edges (see the entry in the lower blue row of the table).
Shown below are the numbers of polyhedral vertices (V) and non-polyhedral (C–V) corners, edges (E) and internal sides (e–E) of the triangular sectors of the faces of the first four Platonic solids:
| Polyhedron |
V |
C–V |
E |
e–E |
Total |
| Tetrahedron |
4 |
4 |
6 |
12 |
26 |
| Octahedron |
6 |
8 |
12 |
24 |
50 |
| Cube |
8 |
6 |
12 |
24 |
50 |
| Icosahedron | 12 |
20 |
30 |
60 |
122 |
| Total = | 30 |
38 |
60 |
120 |
248 |
Notice how the Godname YAHWEH with number value 26 prescribes the tetrahedron (the simplest Platonic solid) with 26 corners & sides of the 12 triangles in its four faces. Notice also that the octahedron and cube each has 26 corners & polyhedral edges and 50 corners & sides, where 50 is the number value of ELOHIM, the Godname of Binah. The 24 triangles in the faces of each of these two polyhedra have 36 sides, where 36 is the number value of ELOHA, the Godname of Geburah, which is the Sephirah next below Binah on the Pillar of Judgement.
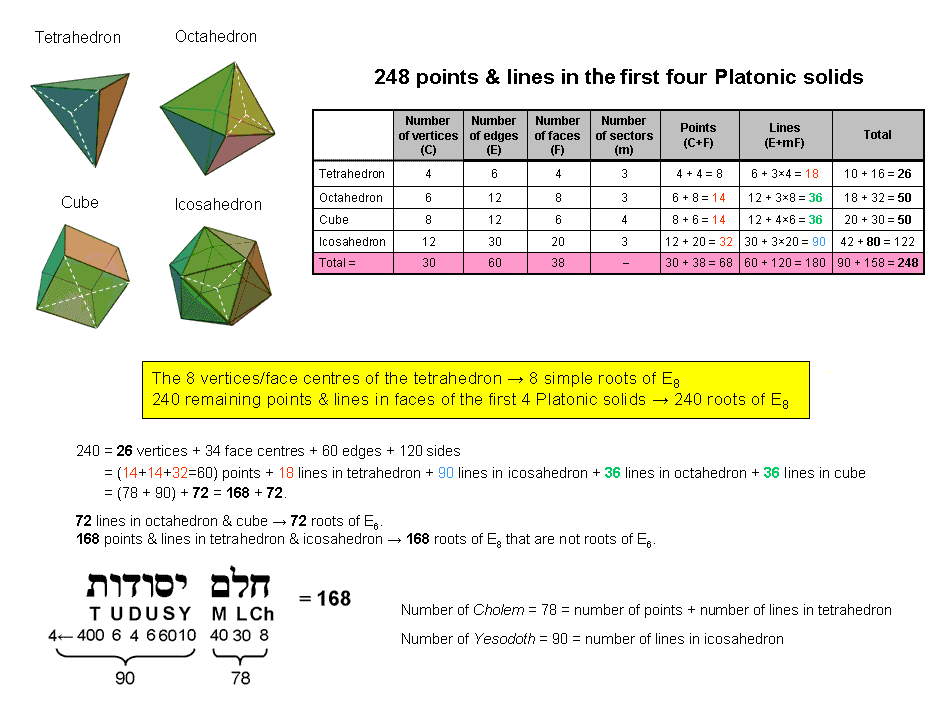
The four vertices and the four face-centres in the tetrahedron constitute eight points, so it seems, intuitively speaking, more natural to associate these points belonging to the simplest Platonic solid with the eight simple roots of E8, rather than the eight centres of the faces of the octahedron or the eight vertices of the cube. The remaining 240 points and straight lines making up the first four Platonic solids would then correspond to the 240 roots of E8.
There are 18 lines in the tetrahedron and (14+14+32=60) points in the octahedron, cube & icosahedron (see table in adjacent diagram). Hence, they form a set of 78 points & lines. The icosahedron has 90 lines. There are (78+90=168) points & lines other than the (36+36=72) lines in the octahedron & cube. 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, 78 being the number of Cholem and 90 being the number of Yesodoth.
The number 72 could be the sum of other combinations of numbers in the table. However, it is readily verified that the simplest and most natural combination is the pair of numbers 36. Article 53 proves that sacred geometries embody the number 240 and that it displays the factorization 10×24. As this can be written as a tetractys array of the number 24, it means that we should expect the number 72 appearing in the geometrical composition of the faces of the first four Platonic solids to display the factorization 3×24, if it refers to the correct combinations, for it would then correspond to the integers 24 at the three corners of the array. This, indeed, is the case for the 72 lines in the octahedron and cube, which have 24 edges, each polyhedron having 24 more sides of sectors. Notice also that, as the tetrahedron has eight points in its faces, namely, four vertices & four centres of faces, the number 80 (=8+72) arises naturally in the geometrical composition of the first four Platonic solids. The division:
248 = 80 + 168
is characteristic of holistic systems (an example was encountered in Superstrings as sacred geometry/Tree of Life). How sacred geometries embody the number 248 and its 8:72:168 division is discussed in The holistic pattern.
The fact that the first four Platonic solids embody the holistic parameter 248 in their geometry illustrates the Tetrad Principle formulated in Article 1. It states that the first four members of a class of mathematical object or, alternatively, the fourth member of that class, always express parameters of holistic systems. As further illustration of this principle, it will be shown on page 5 that the first four Platonic solids also embody in a natural way the superstring structural parameters 168, 336, 840 & 1680 established by C.W. Leadbeater over a century ago when he remote-viewed atoms and their UPA/superstring constituents (see Occult Chemistry). This is tantamount to proof that Leadbeater did, indeed, describe superstrings paranormally, for the chance that all four numbers implicit in Leadbeater's description of the UPA could, by accident, characterize the geometrical compositions of these regular polyhedra is, obviously, extremely small, whilst there is no other conventional explanation for the first four Platonic solids embodying these numbers. These are the only possibilities that need be considered. The natural appearance in the Platonic solids of the dynamical parameter 248 of the E8×E8′ heterotic superstring and these four structural parameters of its subquark state (namely, the UPA) renders totally untenable any contention by a sceptic towards the paranormal that their presence has been contrived by convoluted analysis. There is nothing artificial or convoluted about the simple way in which all five numbers emerge from the analysis as geometrical properties of the Platonic solids (see page 5).
| << Previous [1] 2 3 4 5 ...8 Next >> |