| << Previous [1] 2 3 4 5 ...18 Next >> |
The disdyakis triacontahedron

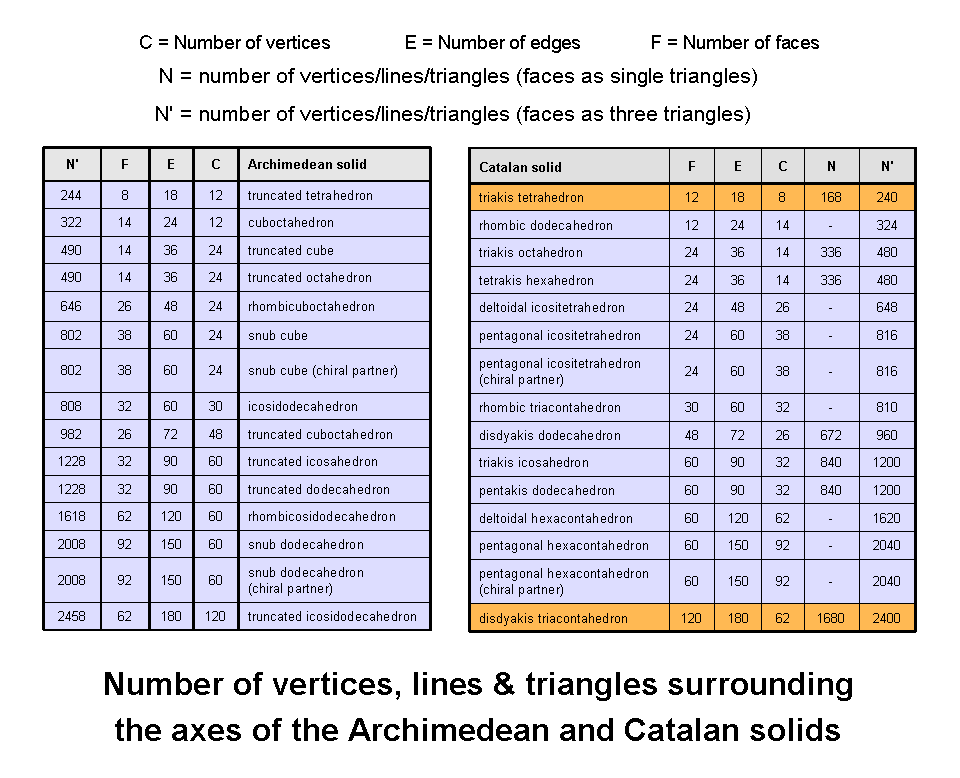
There are 13 polyhedra (Archimedean solids) whose faces consist of two or more regular polygons meeting in identical vertices. Interchanging vertices and faces generates the dual of a polyhedron. The duals of the Archimedean solids are the Catalan solids. The table lists the 13 Archimedean solids and their 13 duals in the order (starting from the top) of increasing number of vertices for the former and increasing number of faces for the latter. The Catalan solid with the fewest number of vertices and faces is the triakis tetrahedron (see table above). It is a tetrahedron with tetrahedra stuck on its faces (see here). The Catalan solid with the most faces (but not the most vertices) is the disdyakis triacontahedron. This was discussed in Sacred geometry/Polyhedral Tree of Life as the "outer" form, or Yin aspect, of the polyhedral version of the Tree of Life (see Article 23), its inner form (Yang aspect) being a polyhedron with 144 faces (the so-called "144 Polyhedron").
Suppose that the faces of the Archimedean and Catalan solids are each divided into their sectors. Suppose, furthermore, that the internal triangles formed by their centres and edges are divided into sectors. How many points, lines & triangles are needed to do this? The table lists the numbers N′ for these polyhedra. It also lists the numbers of geometrical elements for polyhedra with triangular faces which are not divided into their sectors (polyhedra with non-triangular faces have cells with dashes). We see that the disdyakis triacontahedron is the only one of the 26 polyhedra (30, if chiral counterparts are included) that has 2400 geometrical elements surrounding an axis that passes through two diametrically opposite vertices. Moreover, it is the only polyhedron with triangular faces that has 1680 such elements when they are not divided into sectors. The uniqueness of these properties is due to the status of the last of the Catalan solids as the outer aspect of the Polyhedral Tree of Life. The 1680 elements represent bits of geometrical information needed to build its 3-dimensional form. They are the counterpart of the 1680 turns in the helical whorls of the E8×E8 heterotic superstring (see here).
The table indicates that 720 geometrical elements are added when the 120 triangular faces of the disdyakis triacontahedron are divided into their 360 sectors. The division:
2400 = 720 + 1680
is the polyhedral counterpart of the division of the 240 roots of E8 into the 72 roots of its exceptional subgroup E6 and the 168 extra roots of E8. Indeed, the 72 Yang-Mills gauge fields associated with the former have 720 space-time components and the 168 Yang-Mills gauge fields associated with the latter have 1680 space-time components because each gauge field exists in 10-dimensional space-time.
The encoding in sacred geometries of the oscillatory form of the whorls of the subquark state of the E8×E8 heterotic superstring is discussed in many of the author's articles on this website, starting with Article 22 (WEB, PDF).
| << Previous [1] 2 3 4 5 ...18 Next >> |