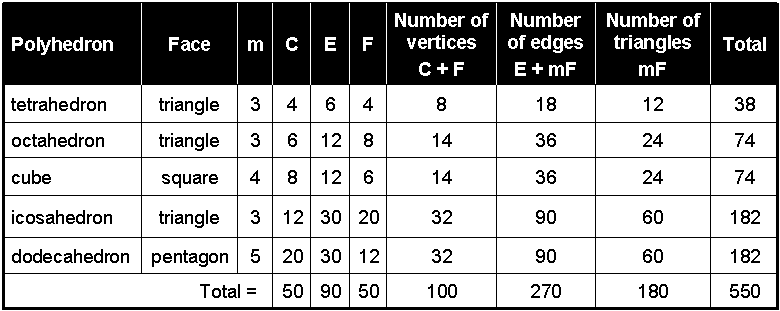
An m-sided regular polygon has m sectors. A regular polyhedron with C vertices, E edges & F faces have mF sectors with (C+F) corners and (E+mF) sides. When the faces of the five Platonic solids are divided into their sectors, the table above shows that they have 550 points (corners), lines (sides) & triangles, where 550 = 10(1+2+3+4+5+6+7+8+9+10) = 10×55, where 55 is both the tenth triangular number and the tenth Fibonacci number (see Article 50 (Part 1) & Article 50 (Part 2) for the definition of Fibonacci numbers and how they appear in sacred geometries). This is another amazing example of how the Decad (10) determines the geometry of the five Platonic solids. The appearance of this number is striking evidence that they are the regular polyhedral representation of the "Cosmic Tree of Life" (see also Maps of Reality/Platonic solids). They contain 500 (=50×10) geometrical elements other than their 50 vertices. This shows how ELOHIM, the Godname of Binah with number value 50, prescribes the geometrical composition of this archetypal system. Each half of a Platonic solid has on average 50 corners, sides & triangles in its faces other than vertices.

More details about the properties of the Platonic solids and their prescription by the Divine Names can be found in Article 3 (WEB, PDF).

<< Previous    1...   15  16  17  [18]  19    Next >>

Home