#30 The superstring structural parameter 1680 embodied in the outer & inner forms of 10
 overlapping Trees of Life, the first four Platonic solids & the disdyakis triacontahedron

The number of yods below the top of the nth Tree in any set of overlapping Trees of Life with Type A triangles is given by:

N(n) = 158n + 100.

Below the top of the tenth Tree of Life are N(10) = 1680 yods.

As the top of the tenth Tree is the 65th SL, ADONAI, the Godname of Malkuth with number value 65 (see here) prescribes the superstring structural parameter 1680.

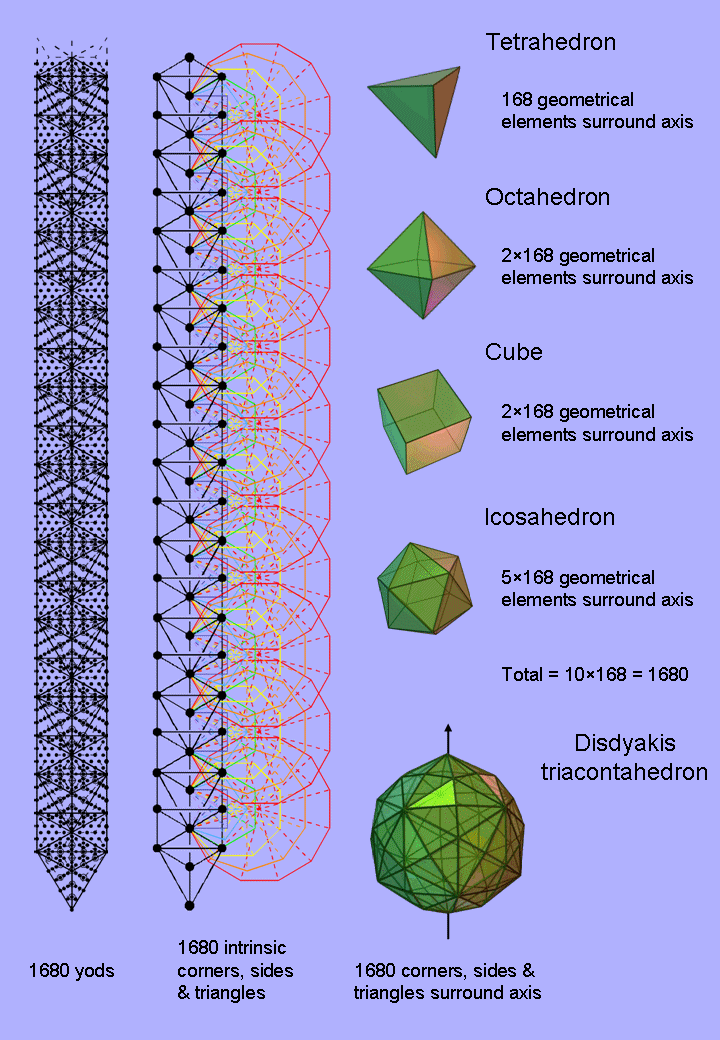
The seven enfolded polygons of the inner Tree of Life have 168 corners, sides & sectors outside the root edge that are unshared with the outer Tree of Life. The 70 polygons enfolded in 10 overlapping Trees of Life have 1680 geometrical elements outside their root edges that are intrinsic to them.

When the F faces of a Platonic solid with E edges are divided into their n sectors and their vertices & face centres are joined to the centre of each polyhedron, the number of corners, sides & triangles that surround an axis passing through two opposite vertices is 10E + 9nF. The tetrahedron (E = 6; nF = 12) has 168 such geometrical elements, both the octahedron (E = 12; nF = 24) & cube (E = 12; nF = 24) have 336 elements and the icosahedron (E = 30; nF = 60) has 840 elements. The axes of the first four Platonic solids, which the ancient Greeks believed were the shapes of the particles of the elements of Fire, Water, Earth & Air, are surrounded by 1680 geometrical elements (840 in the tetrahedron, octahedron & cube and 840 in the icosahedron).

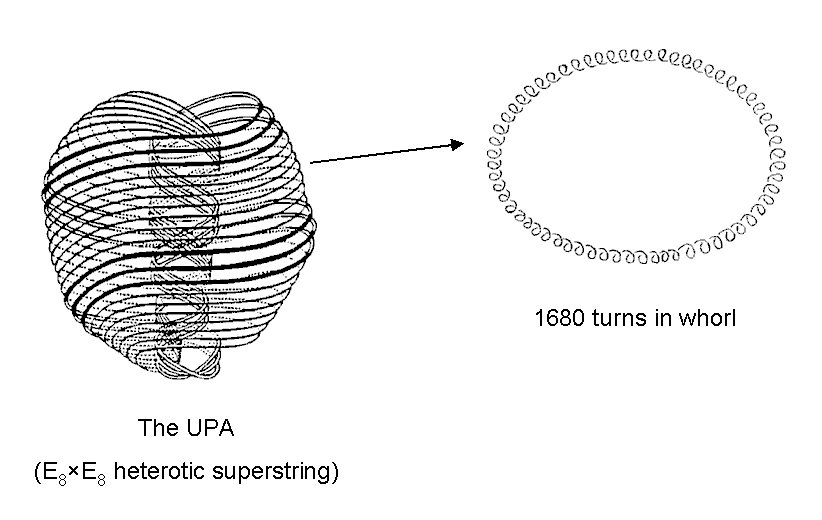
As the dodecahedron has the same number of edges as the icosahedron and the same number (60) of sectors in its faces, the formula (10E+9nF) tells us that the same number (840) of geometrical elements surround the axes of each Platonic solid. Together, they have 1680 geometrical elements surrounding their axes. This is the counterpart of the 840 circular turns in an outer half and in an inner half of each whorl of the UPA.

When the 62 vertices of the disdyakis triacontahedron are joined to its centre and the resulting 180 internal triangles divided into their 540 sectors, there are 1680 corners, sides & triangles making up its faces and interior that surround an axis passing through two diametrically opposite vertices (see last paragraph in #29).

These are four examples of how sacred geometries embody the number 1680 determined by C.W. Leadbeater at the beginning of the twentieth century as the number of circular turns in each of the ten closed helices making up the basic unit of matter revealed by his micro-psi vision. They are among the most remarkable examples of the analogous properties of the sacred geometries discussed on this website.

<< Previous    1...   28  29  [30]  31  32  ...81    Next >>

Home