| << Previous 1... 31 32 [33] 34 35 ...81 Next >> |
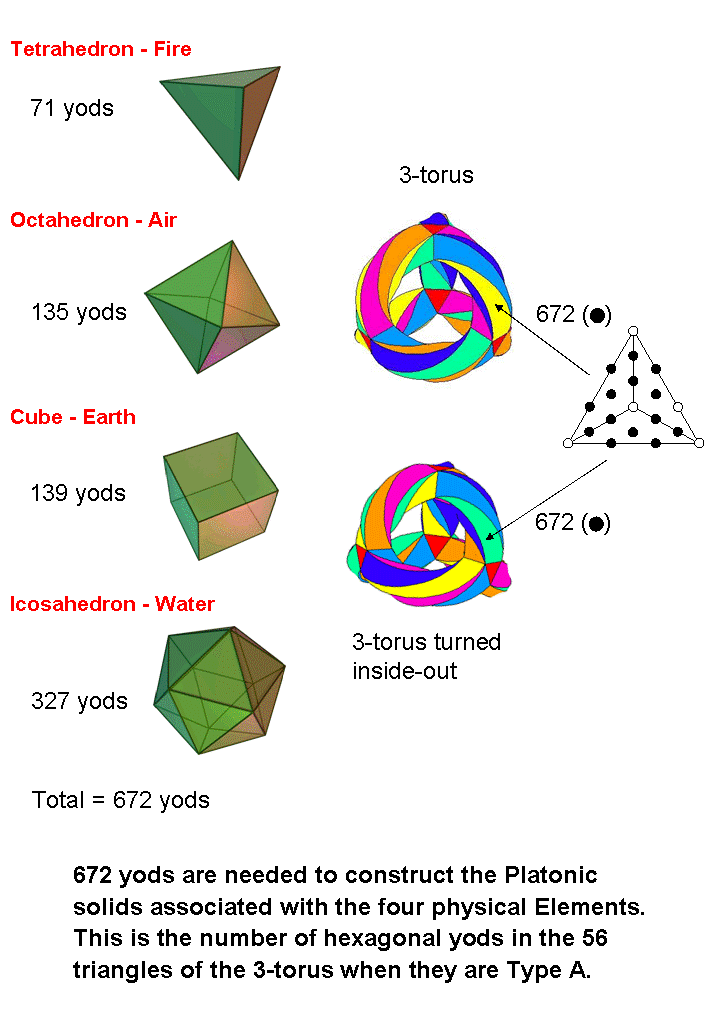
#33 Correspondence between the first four Platonic solids and the 3-torus tiled with 56 Type A triangles

Suppose that the Platonic solids are constructed out of the tetractys — the universal template of sacred geometry. The table in #16 at Sacred geometry/Platonic solids indicates that, including their centres, the tetrahedron consists of 71 yods, the octahedron has 135 yods, the cube has 139 yods and the icosahedron has 327 yods. The first four Platonic solids are made up of 672 yods — an average per solid of 168 yods. This is another way in which the first four Platonic solids embody the superstring structural parameter 168.
Now consider the 3-torus assembled from four triangular prisms and six square antiprisms (see Article 43 for details of its construction). Let us regard each of their 56 triangular faces when assembled as Type A, so that they are imagined as divided into their 168 sectors and each sector then turned into a tetractys (now deformed, as the surface in which each one lies is hyperbolic, not planar). Notice the appearance of the superstring structural parameter 168 (well, of course, it was present before the dividing of each triangle into its sectors because the tiled 3-torus maps the 168 symmetries of the Klein quartic — see also here). The table below lists the yods making up the 168 tetractyses in the 3-torus:
|
Type A Triangle |
|||
|
Triangular prism |
Square antiprism | Total | |
| Number of vertices | 32 | 48 | 80 |
| Number of sides | 60 | 192 | 252 |
| Number of triangles | 24 | 144 | 168 |
| Number of geometrical elements | 116 | 384 | 500 |
| Number of hexagonal yods on sides of tetractyses | 120 | 384 | 504 |
| Number of hexagonal yods | 144 | 528 | 672 |
| Number of yods on sides of tetractyses | 152 | 432 | 584 |
| Number of yods | 176 | 576 | 752 |
(the entries are from Table 3 on page 11 of Article 43). Whether it is the 3-torus or its version turned inside out, we see that
its tetractyses have 672 hexagonal yods. But it was pointed out above that this is the number of yods needed to
build the first four Platonic solids out of tetractyses! Moreover, the average number of yods needed to
construct one of them is 168, which is both the number of symmetries of the Klein quartic and
the number of tetractyses covering the 3-torus! The appearance of the same number in two geometrical systems
which, superficially, have nothing in common, is of course no accident. It is an indication that
both are holistic systems that are parameterized by the same set of numbers, some of which (like
248) are known to theoretical physicists. For example, the triangular sectors of the faces of
the first four Platonic solids have 248 corners & sides, whilst the 56 triangles
covering the 3-torus have 248 yods when they are tetractyses,
168 hexagonal yods lining their sides (see #25 at Wonders of sacred
geometry/superstrings).
Notice that, according to the table, the number of geometrical elements (i.e., points, lines & triangles) making up the 168 hyperbolic triangles = 500 = 10×50. This is how ELOHIM, the Godname of Binah with number value 50, prescribes the archetypal geometrical system of the tessellated 3-torus (Article 43 discusses other examples of its prescription by the Divine Names). Notice also that the 168 tetractyses have 80 corners. 80 is the number value of Yesod (see here). They comprise the 48 corners of the 144 tetractyses making up the six "edges" of the 3-torus deformed into a tetrahedron and the 32 corners of the 24 tetractyses in the four triangular prisms. 48 is the number value of Kokab, the Mundane Chakra of Hod. This 48:32 division manifests in the 80 yods making up the 1-tree because there are 48 red yods up to (and including) Chesed, the first Sephirah of Construction, and 32 black yods above it:
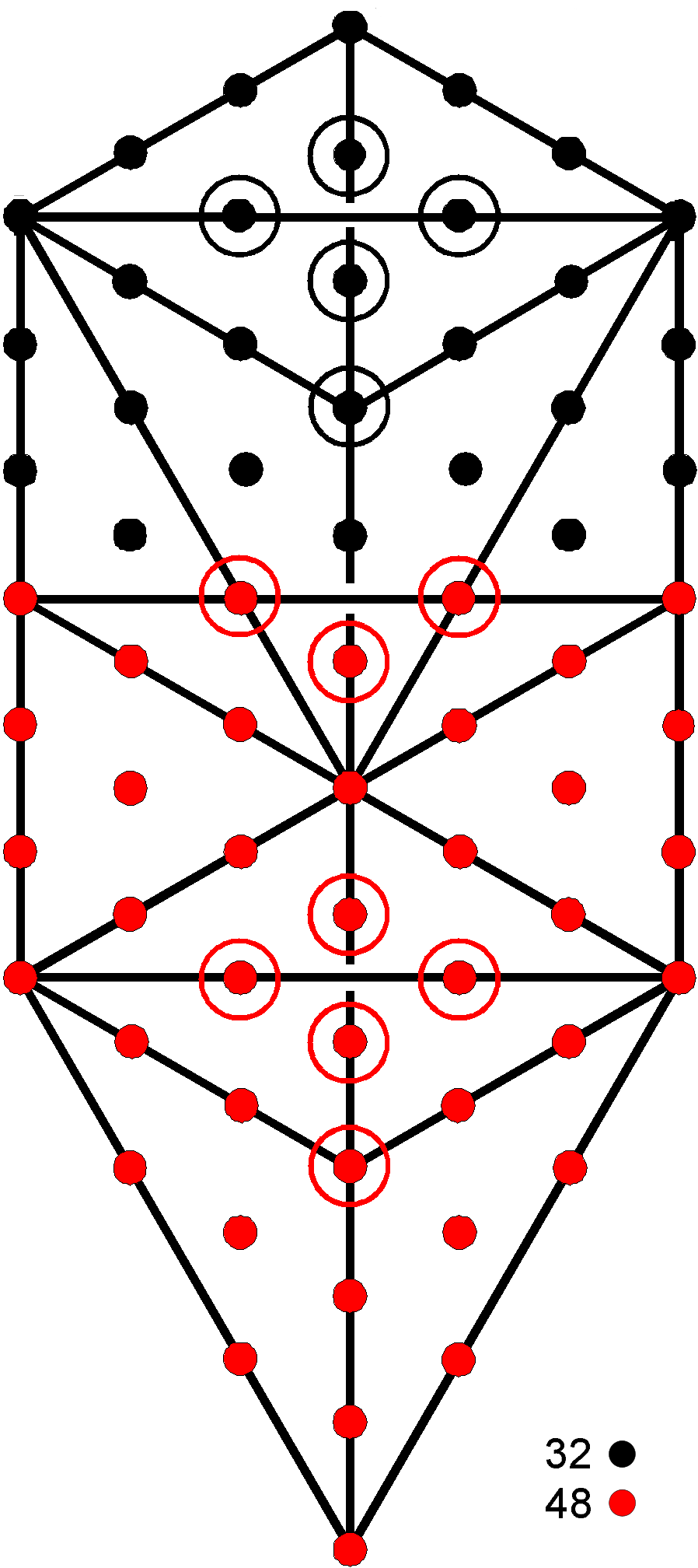
This parallel indicates the Tree of Life character of the tiled 3-torus. Its four "vertices" created by the four triangular prisms with 32 corners of the 24 tetractyses in their eight triangular faces play the role of the pre-formative region of the 1-tree above the first Sephirah of Construction, whilst its six "edges" shaping the surface of the 3-torus fulfill the form-generating function of the seven Sephiroth of Construction.
| << Previous 1... 31 32 [33] 34 35 ...81 Next >> |