| << Previous 1... 23 24 [25] 26 27 ...56 Next >> |
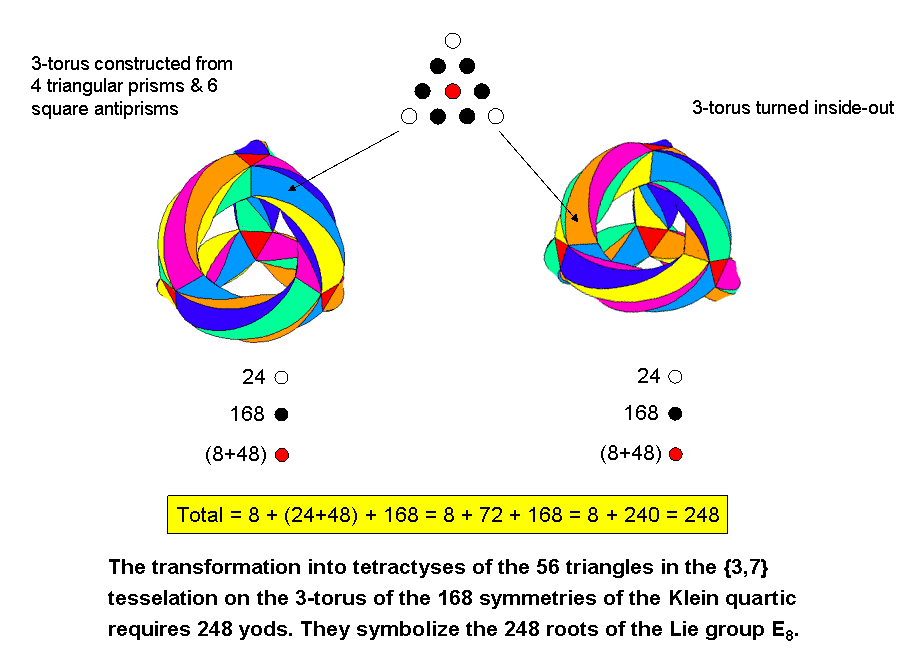
#25 The 248 yods in the 56 triangles-as-tetractyses in the {3,7} tessellation on the 3-torus of the 168 symmetries of the Klein quartic denote the 248 roots of E8
(Advice: because of the technical nature of this topic, some readers may wish, firstly, to study background material presented in Article 15 (p. 24-27) & Article 43).

The 3-torus is a hyperbolic surface of genus 3, that is, it has negative curvature and three holes. As discussed in Article 43, it may be constructed by sticking the square faces of six square antiprisms to the square faces of four triangular prisms. The resulting 56 hyperbolic triangles are the {3,7} mapping of the 168 automorphisms of the famous mathematical equation known as the Klein quartic:
X3Y + Y3Z + Z3X = 0,
where X, Y & Z are complex variables. The 56 triangles consist of the four pairs of triangles at the "vertices" of the tetrahedrally-deformed 3-torus and six sets of eight triangles that form its "edges." Suppose that each triangle is transformed into a tetractys. As each triangle is on a hyperbolic surface, the tetractyses will, of course, be deformed. But they, still, have four yods along each of the 84 edges of the prisms and antiprisms. The yod composition of the 56 tetractyses is shown below:
| Triangular prism |
Square antiprism |
Total | |
| Number of vertices | 4×6 = 24 | — | 24 |
| Number of edges | 4×9 = 36 | 6×8 = 48 | 84 |
| Number of triangles | 4×2 = 8 | 6×8 = 48 | 56 |
| Number of geometrical elements | 68 | 96 | 164 |
| Number of hexagonal yods on sides of tetractyses | 2×36 = 72 | 2×48 = 96 | 168 |
| Number of hexagonal yods | 8 + 72 = 80 | 48 + 96 = 144 | 224 |
| Number of yods on sides of tetractyses | 24 + 72 = 96 | 96 | 192 |
| Number of yods | 8 + 96 = 104 | 48 + 96 = 144 | 248 |
We see that they contain 248 yods made up of eight red hexagonal yods at the centres of the opposite faces of the four triangular prisms, 72 black hexagonal yods on the 36 sides of their eight tetractyses, 24 white corners of tetractyses and 144 hexagonal yods (48 red, 96 black) in the 48 tetractyses of the six square antiprisms:
248 = 8 + 72 + 24 + 144 = 8 + 240.
The eight hexagonal yods denote the eight simple roots of the rank-8 Lie group E8 and the 240 corners & hexagonal yods denote its 240 roots. The latter include 168 black hexagonal yods on the 84 sides of the triangular prisms & square antiprisms, 24 white corners & 48 red hexagonal yods at the centres of the 48 tetractyses in the six "edges" of the tetrahedron into which the 3-torus can be deformed, i.e., (24+48=72) corners & central hexagonal yods. The division:
240 = 72 + 168
corresponds to the 72 roots of E6, the rank-6, exceptional subgroup of E8, and the remaining 168 roots of the latter.
Turned inside-out, the 3-torus comprises 56 hyperbolic triangles that are the {3,7} mapping of the 168 anti-automorphisms of the Klein quartic. As tetractyses, they have the same numbers of yods distributed in the same subsets as those in the 3-torus. Both 3-tori contain (248+248=496) yods, where 496 is the number value of Malkuth. Their yod compositions are analogous, therefore, to the root structure of E8×E8, one of the two possible gauge symmetry groups of the heterotic superstring (see here under heading "Superstring gauge symmetry group").
The number 248 is a parameter of holistic systems, being the number value of Raziel, the Archangel of Chokmah. Its presence in the {3,7} tiling of the 3-torus and its version turned inside-out, as well as the fact (discussed above) that it displays the other parameters and patterns of holistic systems, strongly suggests that both tori are connected to the physics of the E8×E8 heterotic superstring in some way to be determined. This is further strongly suggested by the fact that there are 192 yods lining the sides of the 56 tetractyses and that this number divides up into the 24 vertices of the prisms & antiprisms and the 168 hexagonal yods on the 84 sides of the tetractyses. This 24:168 division is characteristic of holistic systems, as explained in The holistic pattern, as it reflects the difference between the function of the Supernal Triad (symbolized by yods at corners of tetractyses) and the seven Sephiroth of Construction (symbolized by hexagonal yods). Many examples are discussed on this website.
| << Previous 1... 23 24 [25] 26 27 ...56 Next >> |