#35 Correspondence between the 248 yods below the top of the 1-tree and the 248 yods in the 3-torus tiled with tetractyses

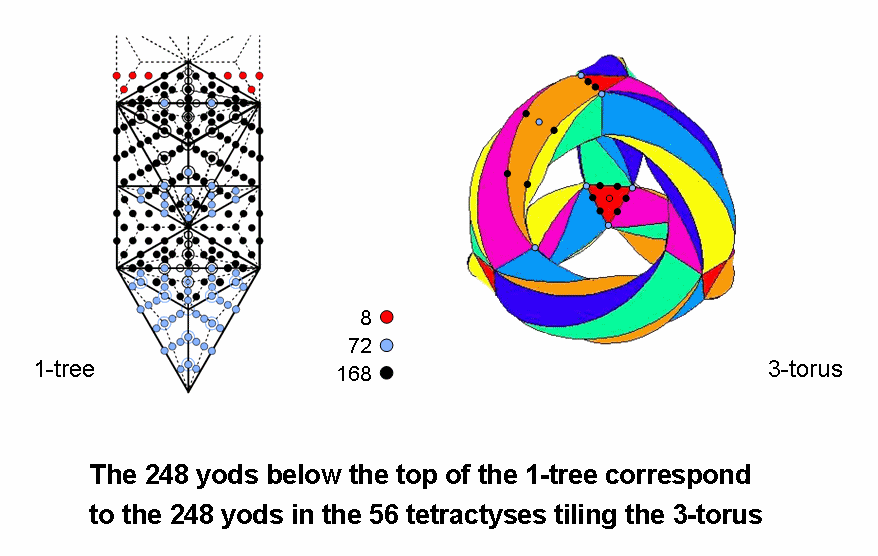
When the 19 triangles in the 1-tree are Type A triangles, it contains 240 yods other than the 11 SLs at their corners. They are the extra yods needed to construct the 1-tree from Type A triangles. The trunk of the Tree of Life:

• point (Kether);
• line (Chokmah-Binah Path);
• triangle (Chesed-Geburah-Tiphareth);
• tetrahedron (Netzach-Hod-Yesod-Malkuth).

(see also #25 in this section) contains 80 yods, i.e., 70 blue yods other than SLs. The root of the Tree of Life is the Path joining Daath (Yesod of the second Tree) to Tiphareth. It has two blue hexagonal yods. The root & trunk contain 72 blue yods. The branches of the 1-tree (namely, what is outside its root & trunk) contain (240−72=168) black yods. Hence, the 240 yods in the 57 tetractyses other than the 11 SLs of the 1-tree comprise 72 blue yods in its root & trunk and 168 black yods in its branches. Below its apex on one side of the central Pillar of Equilibrium are four red hexagonal yods in two tetractyses that belong to the second Tree and four red hexagonal yods in two tetractyses on the other side that are their mirror images. Starting from a mathematical point (Kether), 248 extra yods in (57+2+2=61) tetractyses are needed to build the lowest Tree of Life. They symbolize the 248 roots of the rank-8 Lie group E₈. The eight red hexagonal yods symbolize its eight simple roots, the 72 blue yods in its root & trunk denote the 72 roots of E₆, one of the exceptional subgroups of E₈ and the 168 black yods in its branches denote the remaining 168 roots of E₈.

Compare this pattern with the hyperbolic surface of a 3-torus tessellated with 56 triangles which are turned into tetractyses. For the sake of clarity, the diagram shows only one (red) face of a triangular prism turned into a tetractys and only one (orange) face of a square antiprism made into a tetractys. As calculated in #25 at Wonders of sacred geometry/superstrings, their 248 yods consist of:

• eight red hexagonal yods at the centres of the eight triangular faces of the four triangular prisms forming the "vertices" of the tetrahedrally-deformed 3-torus;
• 72 blue yods either at the 24 vertices of these prisms or at the centres of the 48 triangular faces of the six square antiprisms;
• 168 black hexagonal yods on the 84 edges of these faces.

The following one-to-one correspondences exist:

• Eight red yods outside the 1-tree but below its apex ↔ eight red hexagonal yods at the centres of the four pairs of triangular faces of the triangular prisms. The four red yods on one side of the central pillar correspond to the red hexagonal yods at the centres of the outer faces of the triangular prisms and the four red yods on the other side correspond to the red hexagonal yods at the centres of the inner faces of these prisms;
• 72 blue yods in root & trunk of 1-tree ↔ 72 blue yods at the vertices of the four prisms or at the centres of the triangular faces of the six square antiprisms;
• 168 black yods in branches of 1-tree ↔ 168 black hexagonal yods on the edges of the faces of the square antiprisms.

The 3-torus tiled with 56 tetractyses conforms to the archetypal pattern and yod composition of the 1-tree. Such correspondences amount to strong evidence refuting the suggestion that it just happens to be a coincidence that this tiling of the 3-torus from tetractyses requires exactly 248 yods — the number of roots in E₈. If that had been the case, it would be highly unlikely that the analogous breakdown of this number into 8, 72 & 168 could also be a matter of chance, in spite of its natural-looking geometrical basis.

<< Previous    1...   33  34  [35]  36  37  ...81    Next >>

Home