| << Previous 1... 35 36 [37] 38 39 ...81 Next >> |
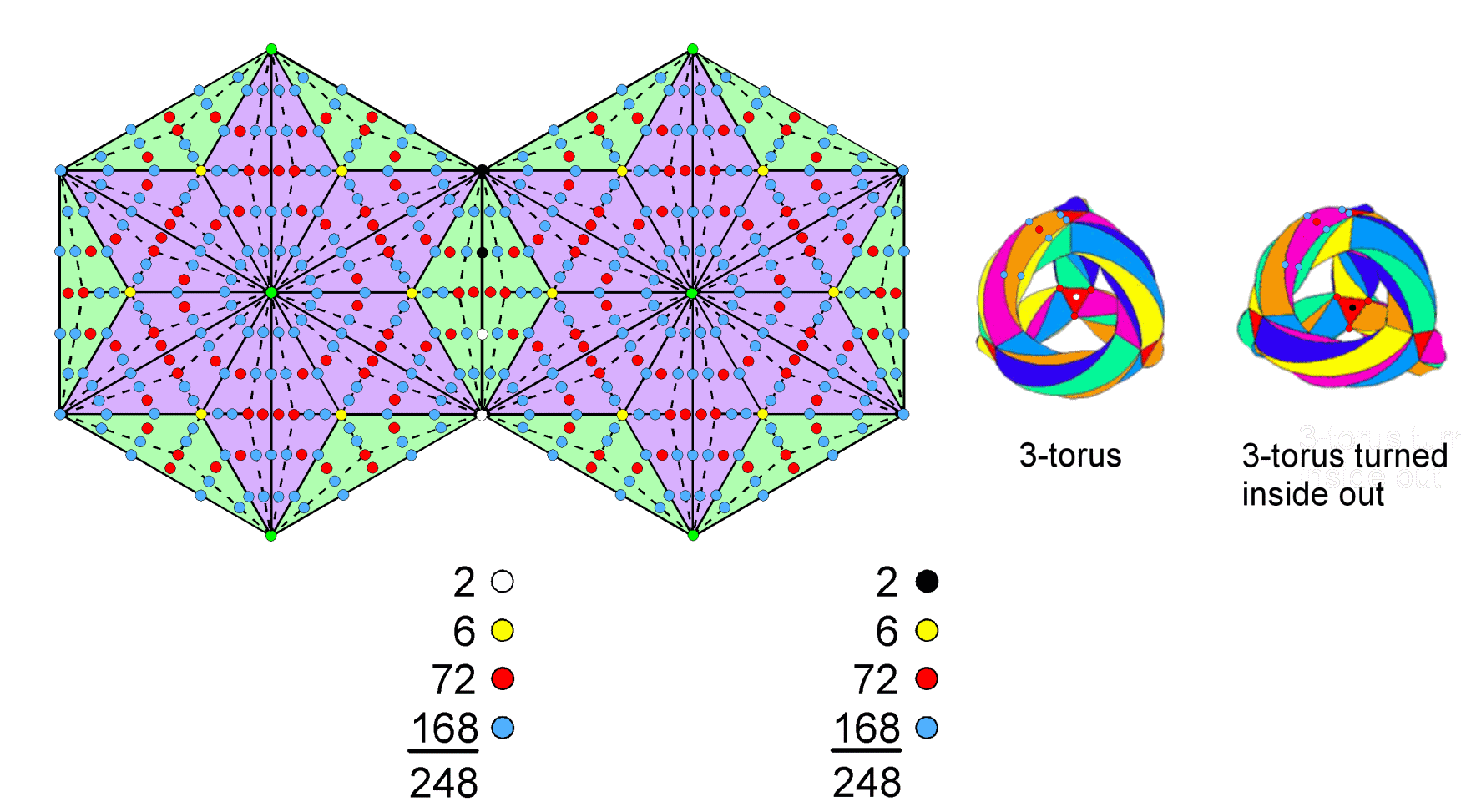
#37 Correspondence between the two enfolded Type C hexagons and the pair of 3-tori tiled with 56 triangles

The number of yods in a Type C n-gon = 42n + 1. A Type C hexagon (n=6) has 252 yods surrounding its centre. 248 of these yods are outside its edge shared with the other hexagon. What this means is that 496 yods outside the root edge of the two enfolded, Type C hexagons surround their centres. This is the dimension of SO(32) & E8×E8, the gauge symmetry groups of the two types of heterotic superstring. The latter corresponds to the pair of similar hexagons. However, as the topmost corner of each hexagon coincides with the lowest corner of each hexagon enfolded in the next higher Tree of Life, the ten pairs of hexagons enfolded in ten overlapping Trees of Life will not have 4960 yods outside their root edges and surrounding their centres that symbolize the 4960 space-time components of the 496 10-dimensional gauge fields of E8×E8. This can be remedied either by including the yod at the centre of each hexagon in each set of 248 yods, so that there are 248 yods per hexagon, or by including two yods on the root edge with each set and excluding the centre, the topmost corner & the lowest corner because they coincide with SLs on the side pillars of the ten Trees, so that 248 yods that are not SLs are associated with each hexagon. As the diagram indicates, the latter possibility is favoured because it provides a natural identification of the two simple roots of E8 that do not belong to its exceptional subgroup E6 with the two yods on the root edge associated with each hexagon. Moreover, the yellow centres of the six sectors of each hexagon would then denote the six simple roots of E6, the 72 red yods at corners and centres of each tetractys would denote the 72 roots of E6 and the 168 blue yods would denote the remaining 168 roots of E8.
As discussed in #35, when the 56 triangles of the 3-torus mapping the 168 symmetries of the Klein quartic are turned into tetractyses, they have 248 yods. The counterparts in the 3-torus and its turned inside-out version of the division:
248 = 2 + 6 + 72 + 168
displayed by the 248 yods in each Type C hexagon are:
(see diagram in #35).
The Tetrad Principle (see Article 1 for its full formulation) determines this correspondence because the hexagon is the fourth regular polygon, whilst the Type C hexagon is the fourth in the sequence: hexagon→Type A hexagon→Type B hexagon→Type C hexagon.