| << Previous 1... 37 38 [39] 40 41 ...81 Next >> |
#39 The 720:240:720 pattern
in the disdyakis triacontahedron and in the 1-tree & (7+7) separate polygons

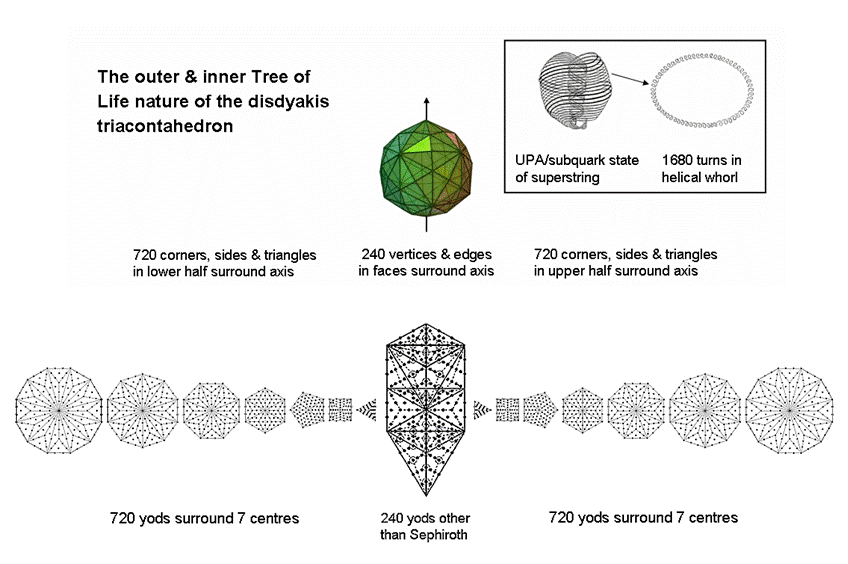
It was pointed out in #29 of this section that 240 corners, 780 sides & 660
triangles surround an axis passing through two diametrically opposite vertices of a disdyakis triacontahedron
when all its vertices are joined to its centre and the 180 resulting triangles divided into their sectors. In
other words, its axis is surrounded by 240 points and 720 lines & triangles in each half of the polyhedron.
Alternatively, as 60 vertices & 180 edges surround the axis, the latter is surrounded by 240 vertices &
edges and 720 points, lines & triangles in each half. Compare this 720:240:720 pattern with the 1-tree and
the two sets of seven separate polygons. When its 19 triangles are Type A, the 1-tree contains 240 yods other
than Sephirothic points. When they are Type B, the seven separate polygons have 720 yods surrounding their
centres.* The pattern 720:240:720 represents the number of yods needed to construct the 1-tree and its inner,
polygonal form, starting from the 11 Sephirothic points in the former and the 14 centres in the latter. The
following correspondences exist:
|
Disdyakis triacontahedron |
1-tree & its inner form |
|
| 240 points (or 240 vertices & edges) | ↔ | 240 yods other than Sephiroth; |
| 720 lines & triangles (or 720 points, lines & triangles) in one half |
↔ |
720 yods surrounding centres of one set of 7 polygons; |
| 720 lines & triangles (or 720 points, lines & triangles) in other half | ↔ | 720 yods surrounding centres of the other set of 7 polygons. |
As shown in #20 of Wonders of superstrings, the same pattern appears in the first four Platonic solids: tetrahedron, octahedron, cube & icosahedron. When their faces are divided into their sectors and when their vertices and face-centres are joined to their centres and the resulting triangles divided into their sectors, their axes are surrounded by 240 corners and 780 sides of 660 triangles (exactly the same as for the disdyakis triacontahedron!), i.e., 720 lines & triangles in each half. As discussed in #27 of this section, the number 720 is determined by the Decad (10) because 720 yods surround the centre of a decagon whose sectors are 2nd-order tetractyses. This number is also embodied in all five Platonic solids because their faces, when constructed from tetractyses, contain 720 hexagonal yods. It appears in the disdyakis triacontahedron as the 720 corners & sides of the 360 sectors of its 120 triangular faces that surround its axis.
Comparison between the three systems displaying this pattern resolves the ambiguity of what the number 240 refers to in the case of the disdyakis triacontahedron. For the first four Platonic solids and the outer and inner form of the 1-tree, this number does not mix different types of things but measures the same type. Hence, the more appropriate measure is the set of 240 points, rather than the 240 vertices & edges. Each yod or geometrical element corresponds to one of the 1680 circularly polarized oscillations (1st-order spirillae) in a helical whorl of the UPA/subquark state of the E8×E8 heterotic superstring. Here are its counterparts in three different (but equivalent) sacred geometries! Why do they appear? Because they are analogous geometrical counterparts of the universal blueprint that manifests in the subatomic world as the 1680 circularly polarized waves of each whorl of a subquark. The "smoking gun" proof of this is discussed in #2 of the section 4-d sacred geometries under the heading "the 421 polytope."
* Proof: number of yods in a Type B n-gon = 15n + 1, where "1" denotes its centre. Number of yods surrounding the centres of the seven Type B polygons = Σ15n = 15Σn = 15×48 = 720.
| << Previous 1... 37 38 [39] 40 41 ...81 Next >> |