#41 The 50:40 division in the Lambda Tetractys, Sri Yantra, Platonic solids, 1st four enfolded polygons & the disdyakis triacontahedron

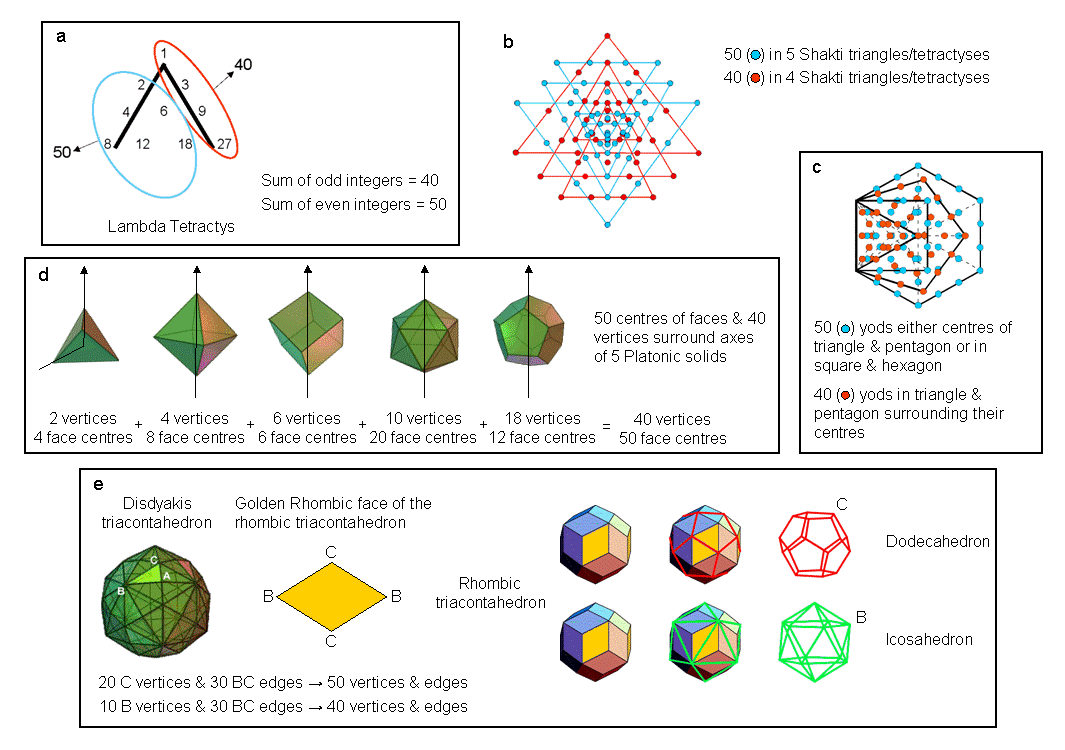
a) The Lambda Tetractys is the tetractys of 10 numbers generated by extrapolating the seven integers making up Plato's Lambda, which formed the basis of his cosmology (see Article 11). Their sum is 90, which is a parameter of all holistic systems. The sum of the four odd integers = 40 and the sum of the six even integers = 50, which is the number value of ELOHIM, the Godname of Binah.

b) The Sri Yantra is created by the interlacing of five downward-pointing triangles (shown as blue) embodying the Shakti, or cosmic feminine, principle, and four upward-pointing triangles (coloured red) that embody the Shiva, or cosmic masculine, principle. Converted to tetractyses, the nine basic triangles are composed of 90 yods, of which 50 belong to the Shakti triangles and 40 belong to the Shiva triangles. This female-male dichotomy corresponds to the ancient Greek characterization of even numbers as feminine and odd numbers as masculine, for the sum of the even integers in the Lambda Tetractys is 50 and the sum of its odd integers is 40.

c) The first four regular polygons of the inner Tree of Life are the equilateral triangle, the square, the pentagon & the hexagon. When they are Type A, they contain, respectively, 19 yods, 25 yods, 31 yods & 37 yods. Outside the root edge of the enfolded polygons are, respectively, 15 yods, 21 yods, 27 yods & 27 yods, i.e., 90 yods. Surrounding the centres of the triangle & pentagon are 40 red yods, leaving 50 blue yods. The polygons with odd numbers of corners — the triangle & pentagon — have 40 yods surrounding their centres, where 40 is the sum of the odd integers in the Lambda Tetractys.

d) Imagine a straight line passing through two diametrically opposite vertices of a Platonic solid (in the case of the tetrahedron, whose vertices are not opposite one another, the axis is an edge — or if we stipulate that the axis must pass through the centre of the tetrahedron, as with the four other Platonic solids — it is a bent line). In either case, the centres of the 50 faces of the five solids and 40 vertices surround their axes that pass through pairs of vertices. If we imagine their faces assembled from triangles, 100 points in space are their corners, 90 of which surround their axes and comprise 40 vertices and 50 face-centres. A 40:50 division underlies the construction of the five Platonic solids that is analogous to that in the nine triangles generating the Sri Yantra.

e) The disdyakis triacontahedron is generated by sticking pyramids onto the 30 Golden Rhombic faces of the rhombic triacontahedron. The 32 vertices of the latter comprise the 12 vertices (labelled B) of an icosahedron and the 20 vertices (labelled C) of a dodecahedron. Its 30 faces have 60 identical edges (BC), 30 edges being in each half of the polyhedron. Surrounding an axis passing through two opposite B vertices are 10 B vertices, 20 C vertices and 30 edges in each half. Hence, the 90 vertices & edges that surround an axis passing through two B vertices of the rhombic triacontahedron divide naturally into sets of 40 (10 B vertices & 30 edges) and 50 (20 C vertices & 30 edges). Dividing each rhombus into its four sectors and then raising them creates the disdyakis triacontahedron. Just as the Sri Yantra is created by nine triangles whose overlap creates a 50:40 division of their 90 yods when they are regarded as tetractyses, so the disdyakis triacontahedron is generated from a polyhedron whose 90 vertices & edges surrounding its axis display an analogous division.

<< Previous    1...   39  40  [41]  42  43  ...81    Next >>

Home