#43 The holistic parameter 236 in the inner Tree of Life, the Type B dodecagon, the 2-d Sri Yantra & the disdyakis triacontahedron

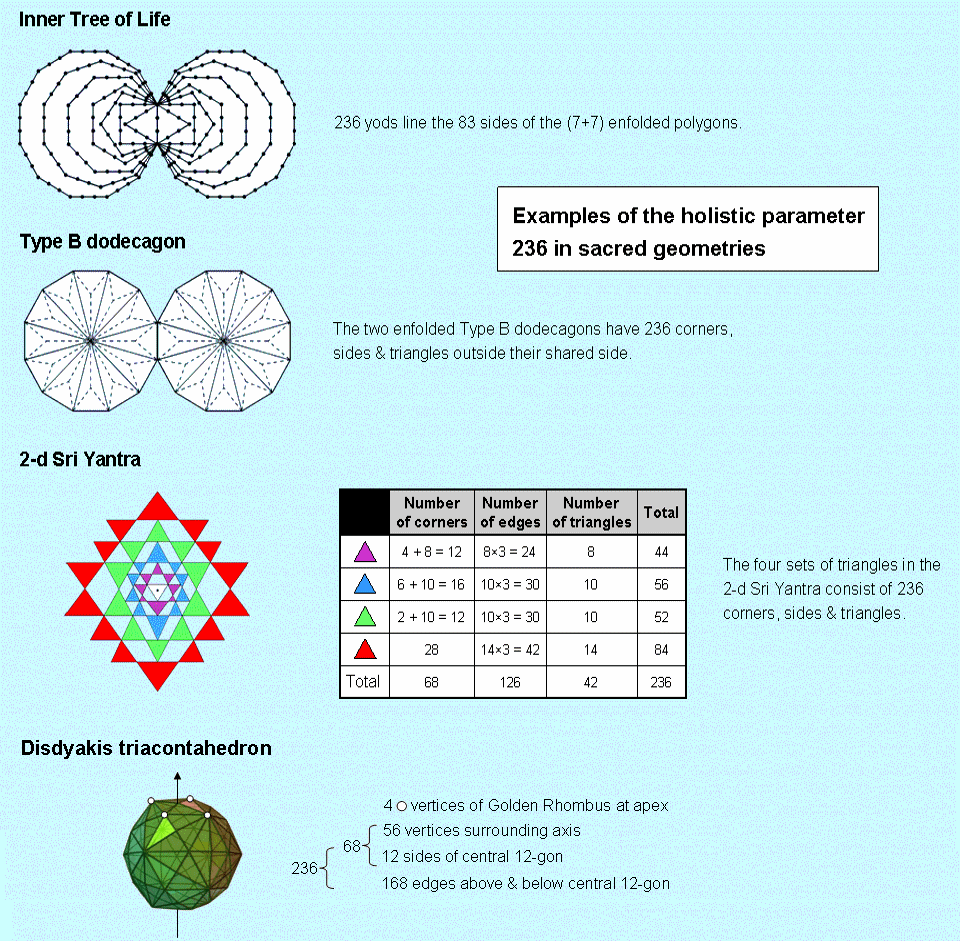
 Inner Tree of Life
236 yods lie on the 83 sides of the (7+7) enfolded polygons of the inner Tree of Life. They comprise 68 corners outside the root edge and 168 other yods.

Type B dodecagon
This dodecagon with its 12 sectors turned into Type A triangles consists of 36 triangles with 25 corners & 60 sides. 120 geometrical elements surround its centre, where

120 = 2² + 4² + 6² + 8².

Two separate Type B dodecagons have 240 geometrical elements surrounding their centres, where 240 = 1×2×3×4×(1+2+3+4). This demonstrates how the integers 1, 2, 3 & 4 express the geometrical composition of the pair of the 10th regular polygons, where 10 = 1 + 2 + 3 + 4. When joined, the two dodecagons have 236 geometrical elements outside their shared edge. They include 22 corners & 46 sides of their 24 sectors, i.e, 68 corners & sides; 168 other geometrical elements (24 corners, 72 sides & 72 triangles) are needed to turn all their sectors into Type A triangles.

2-d Sri Yantra
The table opposite shows that the four sets of triangles that surround the central triangle of the 2-dimensional Sri Yantra are composed of 236 corners, edges & triangles. The first number in each of the top three cells in the "Number of corners" column indicates the number of corners of the violet, blue & green triangles in a set that touch sides of triangles in the next set; the second number indicates the numbers of corners of these triangles that are linked along the bases of each set, e.g., the eight violet triangles in the first set have four corners that touch sides of blue triangles and eight linked corners. There are 68 corners and 168 sides & triangles.

Disdyakis triacontahedron
Consider a disdyakis triacontahedron orientated so that its vertical axis passes through two opposite A vertices. Each of the latter is directly above the centre of a Golden Rhombus, the four white corners of which surround the axis (the diagram shows only one), as do the remaining 56 vertices of the polyhedron. The 12 vertices in its equatorial plane are the corners of a 12-gon with 12 sides. Above and below it are 168 more edges. Surrounding the axis, therefore, are, beside the four vertices of the Golden Rhombus at the top, (56+12=68) geometrical elements that are either vertices or sides of the central 12-gon and 168 other edges, that is, (68+168=236) points & lines.

Here are four sacred geometries that display not only the same number 236 as a measure of their shapes but also its separation into the numbers 68 and 168. In each case, the former number determines the global structure, i.e., corners of polygons/corners & sides of sectors/corners of triangles, and the latter number (the superstring structural parameter) measures the extra geometrical elements needed to construct the sacred geometry from the 'scaffolding' set by the former number. In the discussion in #6 of how the holistic parameter 236 manifests in sacred geometries, it was pointed out that 236 hexagonal yods line the sides of the 72 tetractyses making up the two joined Type B dodecagons. It is remarkable that both the geometrical composition and yod population of the two Type B dodecagons should display this parameter. It is further confirmation of the holistic nature of this regular polygon as the single, polygonal counterpart of the inner Tree of Life. As the tenth regular polygon, the dodecagon when Type B has 176 yods outside the root edge that surround its centre. They symbolise the 176 points, lines & triangles that make up the seven enfolded Type A polygons.

 

<< Previous    1...   41  42  [43]  44  45  ...81    Next >>

Home