| << Previous 1... 42 43 [44] 45 46 ...81 Next >> |
#44 Examples of the holistic parameter 90

Lambda Tetractys
The Lambda Tetractys is the tetractys array of integers generated from the first four powers of 2 & 3 spaced along two of its sides:20 = 1, 21 = 2, 22 = 4, 23 = 8, and 30 = 1, 31 = 3, 32 = 9, 33 = 27.
The red integers 6, 12 & 18 are interpolated from the geometric factors of 2 & 3 determining the two geometric series that conatin these powers of 2 & 3. The sum of the ten integers = 90.
Five Platonic solids
All sacred geometries (and, in general, all holistic systems)
possess this parameter. For example, the five Platonic solids have 90 edges.
Disdyakis triacontahedron
As the polyhedral version of the inner Tree of Life, the
disdyakis triacontahedron has 120 triangular faces with 360 sectors. When its centre is joined to each of its
62 vertices, 180 internal triangles are formed having an edge as one side. They have 540
sectors. The disdyakis triacontahedron is therefore composed of 900 (=90×10) triangles. We discussed in
#41 how 90 vertices & edges surround an axis passing
through two opposite B vertices of the rhombic triacontahedron that underlies the disdyakis triacontahedron.
(7+7) enfolded Type B polygons
The (7+7) enfolded Type A polygons have
(47+47=94) sectors with 80 corners and 175 sides. When each sector is a Type A triangle, 94
corners and (3×94=282) sides are added to what are now (3×94=282) triangles.
282 is the number value of Aralim, the Order of Angels assigned to Binah in the Tree
of Life. Hence, the 282 triangles in the (7+7) enfolded Type B polygons have
(80+94=174) corners and (175+282=457) sides, i.e., there are 913 geometrical
elements. The number of sides outside the root edge is equal to the number of corners & triangles. 910 (=91×10)
geometrical elements are needed to construct the inner Tree of Life, starting with the two endpoints & one
straight line of the root edge. The Cosmic Tree of Life has 91 overlapping Trees (see here). When the red outer Tree of Life is superimposed over its inner form,
we see that Chokmah, Chesed & Netzach coincide with corners of the triangle and hexagon on the right-hand
side and Binah, Geburah & Hod coincide with corners of the triangle and hexagon on the left-hand side. Two
internal sides of the right-hand hexagon form the vertical Pillar of Mercy and two internal sides of the
left-hand hexagon form the Pillar of Judgement. Ten corners & sides of the inner Tree of Life are shared
with its outer form, leaving 900 (=90×10) geometrical elements outside the root edge that are intrinsic to the
14 enfolded polygons.
The geometrical composition of each and both sets of the seven enfolded Type B polygons is shown below:
| Corners | Sides | Triangles | Total | |
| 7 enfolded polygons | 88 | 229 | 141 | 458 |
| (7+7) enfolded polygons | 174 | 457 | 282 | 913 |
The seven enfolded polygons have 88 corners. It is another example of how this parameter appears in sacred geometries, as discussed in #40. Noting that the plane of the polygons contains the outer pillars but not the central Pillar of Equilibrium, this means that six Sephirothic points are shared with the polygons, which contain (913−6=907) geometrical elements other than these points. The number 907 is the 155th prime number, showing in an amazing way how ADONAI MELEKH, the Godname of Malkuth with number value 155, prescribes the geometrical composition of the inner Tree of Life. Each set of seven enfolded polygons have 229 sides (including the root edge) and 229 corners & triangles. 229 is the 50th prime number, showing how ELOHIM, Godname of Binah with number value 50, prescribes each half of the inner Tree of Life. Also, each set has 458 corners, sides & triangles, where 458 is the 229th even integer. Each set has 370 sides & triangles, where 370 = 37×10 and 37 is the 36th integer after 1, showing how ELOHA, the Godname of Geburah with number value 36, prescribes the seven enfolded polygons. Each set has 87 sides outside the root edge, where 87 is the number of Levanah, the Mundane Chakra of Yesod. Each set has 317 corners & sides, where 317 is the 66th prime number, 66 is the 65th integer after 1 and 65 is the number value of ADONAI, part of the Godname of Malkuth.
We pointed in example b of #41 that the nine primary triangles of the Sri Yantra have 90 yods when regarded as tetractyses. In example c of #41, we pointed out that the first four regular polygons of the inner Tree of Life have 90 yods outside their shared root edge when their sectors are tetractyses.
The number of corners & sides in the (7+7) enfolded Type B polygons = 174 + 457 = 631. This is the 150th prime number, where 150 = 15×10 and 15 is the number value of YAH, the Godname of Chokmah. Of these, ten corners & sides are shared with the outer Tree of Life because they make up its two side pillars, leaving 621 intrinsic corners & sides. This is the number of yods that line the sides of the 100 1st-order tetractyses in a decagon whose sectors are 2nd-order tetractyses:
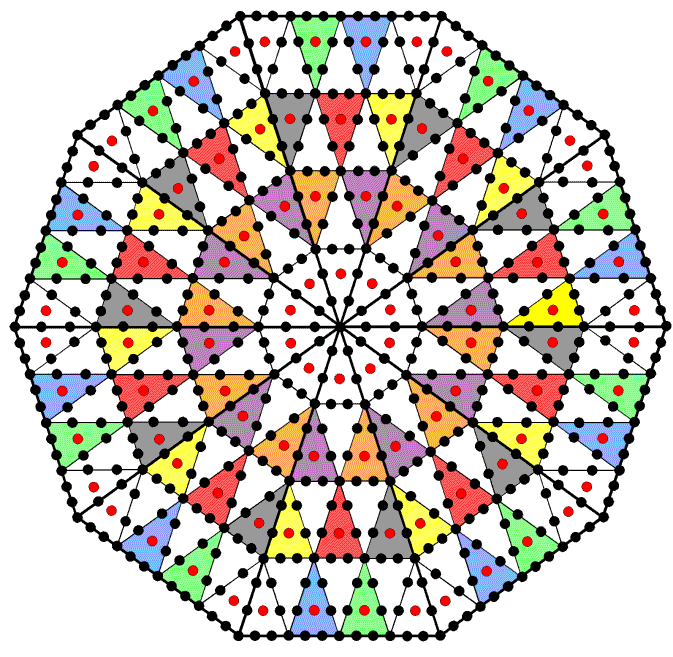
The numbers of intrinsic geometrical elements in each and in both sets of enfolded Type B polygons are shown below:
| Corners | Sides | Triangles | Total | |
| 7 enfolded polygons | 85 | 227 | 141 | 453 |
| (7+7) enfolded polygons | 168 | 453 | 282 | 903 |
900 (=90×10) intrinsic geometrical elements are outside the root edge of both Type B polygons. This shows how the holistic parameter 90 is embodied in the inner Tree of Life. The 141 triangles in the seven enfolded Type B polygons have 85 intrinsic corners, where
85 = 40 + 41 + 42 + 43.
This number is the number of yods in the 2nd-order tetractys (see here), demonstrating the holistic nature of the seven enfolded polygons. Remarkably, the powers of 4 denote the numbers of different sets of corners. 40 = 1 denotes the upper endpoint (the start) of the root edge, 41 = 4 is the number of intrinsic corners inside the triangle, 42 = 16 is the number of intrinsic corners in the square & pentagon and 43 = 64 is the number of intrinsic corners in the hexagon, octagon, decagon & dodecagon:
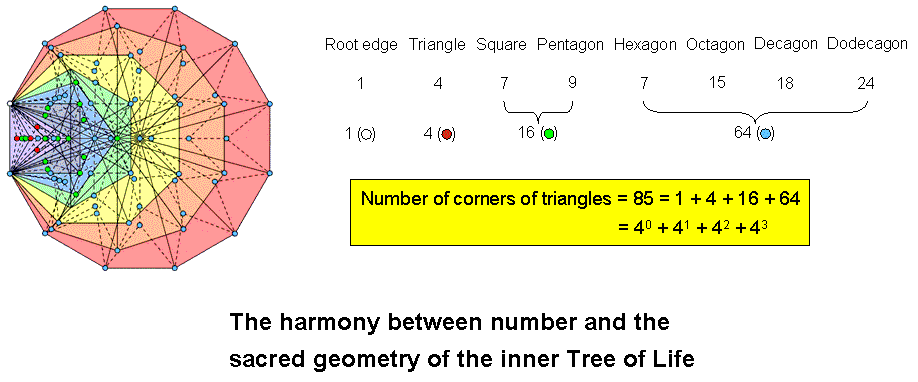
The lower endpoint of the root edge (the finishing point of the right-hand set of polygons) is the last corner of the dodecagon — the last regular polygon in the inner Tree of Life.
Both sets of enfolded polygons have 282 triangles with 168 intrinsic corners, 84 corners being associated with each set. This shows in a simple and remarkable way how the number value of Malkuth is embodied in the inner form of the Tree of Life. The 84:84 division of this parameter of holistic systems arises from the two mirror-image halves of this inner form. The 140 polygons enfolded in ten overlapping Trees of Life have (840+840) intrinsic corners. The manifestation of this in the UPA, the subquark state of the heterotic superstring remote-viewed by Besant & Leadbeater, is the 840 circular turns in the outer half of each helical whorl and the 840 turns in its inner half. Other ways in which sacred geometries encode the three-dimensional form of a whorl are discussed in Wonders of superstrings (in particular, see #18).
The UPA
A point in the 10-dimensional space-time predicted by superstring theory has
nine spatial coordinates. Provided that they do not ever touch or intersect, ten closed curves in this space-time
have single points on them whose locations are determined by a total of (10×9=90) spatial coordinates. The Lambda
Tetractys number 90 is embodied in the ten whorls of the UPA because the basic unit of nuclear matter is a holistic
system whose form is determined by this archetypal pattern.
| << Previous 1... 42 43 [44] 45 46 ...81 Next >> |