| << Previous 1... 32 33 [34] 35 36 ...81 Next >> |
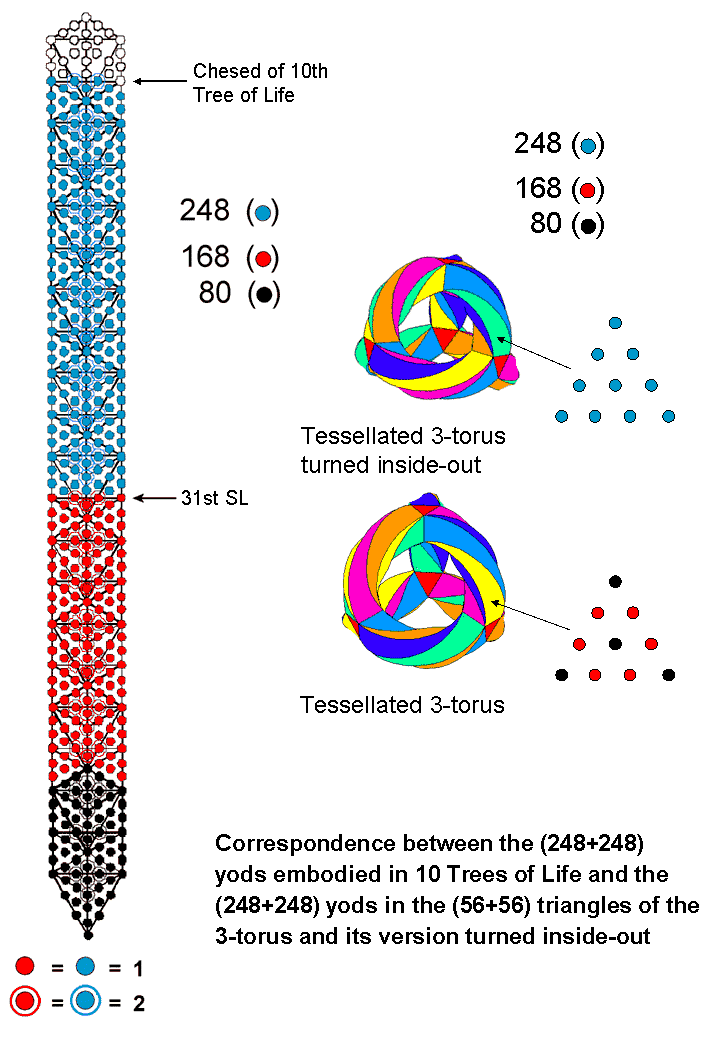
#34 Correspondence between (248+248) yods in the 10-tree, the 248 yods in a tiled 3-torus and the 248 yods in its form turned inside-out

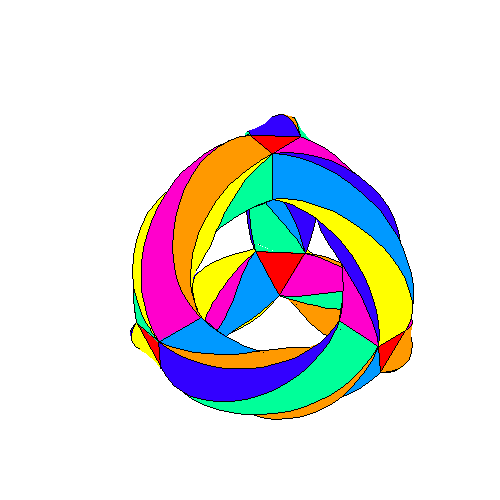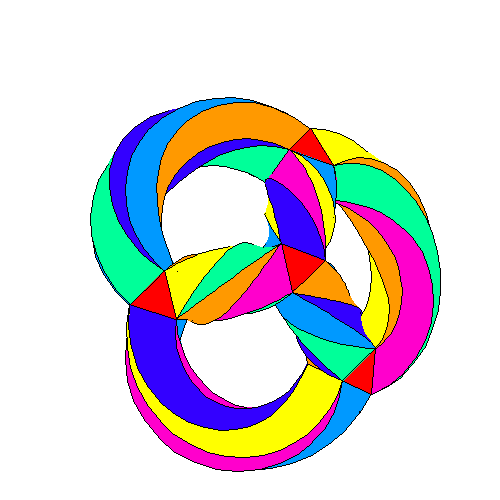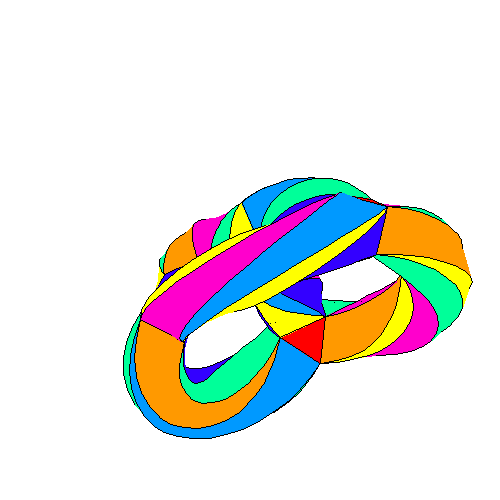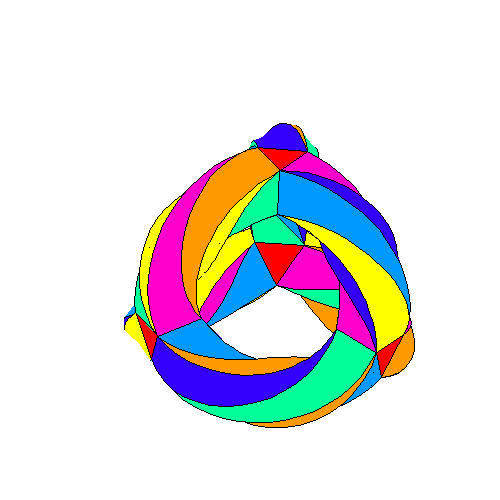
The 3-torus tiled with 56 tetractyses has 248 yods. It turns inside
out into another 3-torus with 248 yods.
(Animated image provided by Greg Egan at http://www.gregegan.net/SCIENCE/KleinQuartic/KleinQuartic.html).
When the triangles of overlapping Trees of Life are turned into tetractyses, there are 248 yods up to Chesed of the fifth Tree. They comprise the 80 black yods in the lowest Tree and a further 168 red yods up to this Chesed. Above it are 248 blue yods up to (but not including) Chesed of the tenth Tree. As ten overlapping Trees of Life are a complete representation of the ten Sephiroth of the Tree, the division of the 496 yods into two sets of 248 yods reflects the basic division of the Tree of Life into its Lower Face spanned by the five lowest Sephiroth (Tiphareth-Malkuth) and the rest of it spanned by the five highest Sephiroth (Kether-Geburah). It is the Kabbalistic basis for the direct product nature of the gauge symmetry group E8×E8 associated with one of the two types of heterotic superstrings. As Chesed of the fifth Tree is the 31st SL and Chesed of the tenth Tree is the 61st SL, where 61 is the 31st odd integer, the Godname EL of Chesed with number value 31 prescribes both the dimension 496 of the two possible, anomaly-free gauge symmetry groups for 10-dimensional superstrings (SO(32) & E8×E8) and the dimension 248 of E8. Another way in which EL prescribes this number at the heart of superstring theory is that 496 is the 31st triangular number:
1 + 2 + 3 + ... + 31 = 496.
As discussed in #25 of Wonders of Superstrings, when the 3-torus is assembled from four triangular prisms and six square antiprisms and their 56 triangular faces are then turned into tetractyses, there are 80 black yods at either the corners (24) or centres (56) of these tetractyses and 168 red hexagonal yods on their 84 sides. We see that a remarkable correspondence exists between the 3-torus, its version turned inside-out and the ten overlapping Trees of Life. The lowest five Trees with 248 yods up to the 31st SL are the counterpart of the tiled 3-torus whose 56 tetractyses have 248 yods. The 80 black yods in the lowest Tree are the counterpart of the 80 black yods at corners and centres of these tetractyses and the 168 red yods above them up to Chesed of the fifth Tree are the counterpart of the 168 red hexagonal yods that line their 84 sides. The 248 blue yods beyond them up to (but not including) Chesed of the tenth Tree are the counterpart of all 248 blue yods in the 3-torus when it is turned inside out. The 5:5 division of the Tree of Life has its counterpart in the 3-torus, which maps the 168 automorphisms of the Klein quartic, and in its turned inside-out version, which maps the 168 anti-automorphisms (rotations plus reflections) of this famous equation in mathematics.
More amazing parallels between the tiled 3-torus and its Tree of Life counterpart are analyzed in Article 43.
| << Previous 1... 32 33 [34] 35 36 ...81 Next >> |