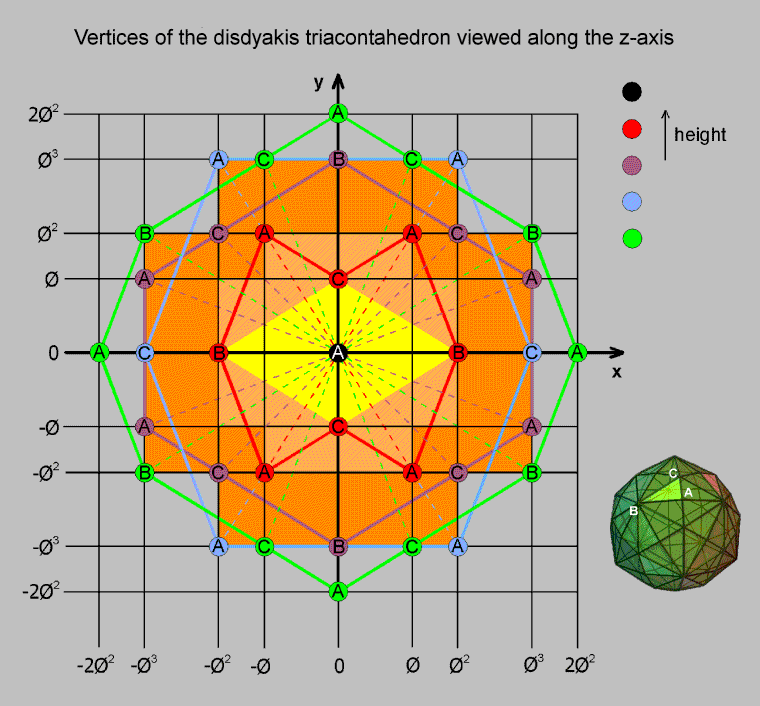
Consider a straight line passing through two diametrically opposite A vertices of the disdyakis triacontahedron as its Z-axis and two perpendicular lines in its central plane as its X- & Y-axes. When the 60 vertices surrounding the Z-axis are projected onto the XY plane, their projections are the corners of seven polygons. The four polygons in the upper half of the polyhedron are denoted by (starting from the XY plane) green, blue, violet & red yods, the two A vertices being at the origin of the coordinate system. Directly underneath the A vertex at the top is a red, 8-sided polygon, then a violet, 10-sided polygon, a blue, 6-sided polygon and, finally, a green, 12-sided polygon in the XY plane. Similar polygons lie underneath this plane. Their corners are located at the intersections of vertical lines spaced at Φ, Φ², Φ³ & 2Φ² along the X-axis and horizontal lines similarly spaced at Φ, Φ², Φ³ & 2Φ² along the Y-axis, where Φ ≈ 1.618 is the Golden Ratio. The four green B vertices in the central 12-sided polygon are at the corners of a Golden Rectangle whose proportions are Φ, as are the four blue A vertices in the 6-sided polygon directly above it. The four A vertices in the uppermost, red polygon also form a Golden Rectangle, whilst its two B and two C vertices are the corners of a Golden Rhombus. The 60 vertices surrounding the Z-axis therefore form five Golden Rectangles. As the disdyakis triacontahedron has 30 A vertices, they form 15 possible such axes, so that 75 Golden Rectangles are formed by these vertices.

<< Previous    1...   8  9  [10]  11  12  ...15    Next >>

Home