| << Previous 1... 66 67 [68] 69 70 ...81 Next >> |
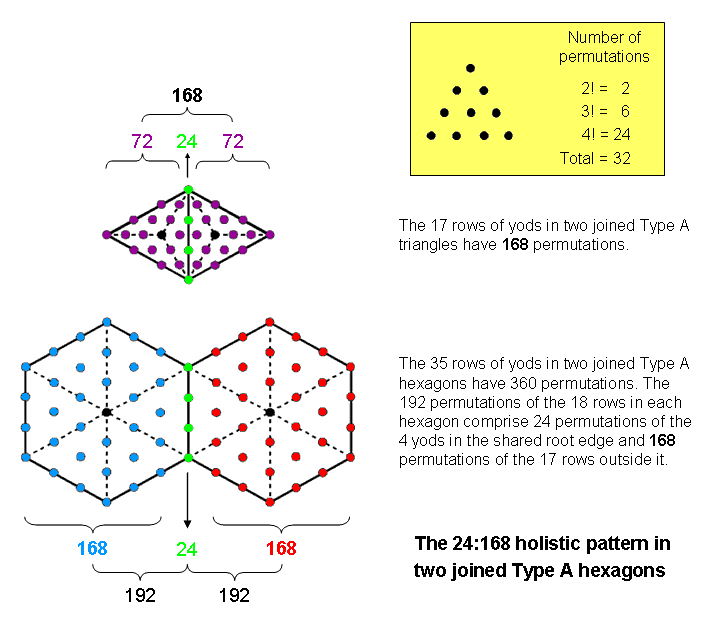
#68 The 24:168 holistic pattern in two joined, Type A hexagons
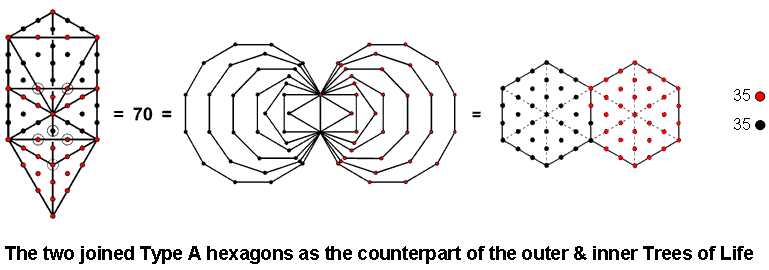
Another reason for the appearance of the 24:168 holistic pattern in the hexagon is that the pair of joined hexagons has 70 yods when their sectors are tetractyses, and this is both the number of yods in the outer Tree of Life and the number of corners of the (7+7) enfolded polygons making up its inner form:

One hexagon corresponds in the outer Tree of Life to its trunk and the other hexagon corresponds to its branches.
We saw in #67 that the 3n rows of yods in an n-gon with tetractyses as its sectors have 32n permutations. It has (32n−24) permutations of its (3n−1) rows outside one side. Two n-gons sharing one side with 24 permutations of its four yods have (32n−24+32n−24+24=64n−24) permutations of their (6n−1) rows. The 17 rows in two joined Type A triangles (n=3) have 168 permutations. This is how the simplest geometrical figure — the triangle — embodies the basic, superstring structural parameter 168, which is the number of Cholem Yesodoth, the Mundane Chakra of Malkuth. The four yods in the root edge have (4!=1×2×3×4) permutations and the (16=42) rows outside it have 144 permutations, where
| 10 | 20 | 30 | 40 | |
| 11 | 21 | 31 | 41 | |
|
144 = |
12 | 22 | 32 | 42 |
| 13 | 23 | 33 | 43 . |
This demonstrates how the Pythagorean integers 1, 2, 3 & 4 symbolised by the four rows of the tetractys express the permutations of the rows in two joined Type A triangles.
 The number of permutations in the five sides of the two joined, Type A triangles = 5×24 = 120
= 22 + 42 + 62 + 82. The second & third
rows in each tetractys have (2+6=8) permutations (see diagram). Each Type A triangle has (3×8=24)
permutations of these rows. Hence, the 168 permutations comprise seven sets of 24
permutations. This is highly significant because Article 53 shows that the parameter 240 embodied in sacred geometries
divides into 72 and 168, where 72 is three sets
of 24 objects or geometrical elements and 168 is seven sets of 24 objects or elements.
This manifests in the subquark state of the E8×E8 heterotic superstring as the 24
E8 gauge charges spread along each of its 10 whorls (72 charges are
spread along its three major whorls and 168 gauges are spread along its seven minor
whorls). The same pattern exists in the tetractyses making up two joined Type A triangles as the seven sets
of 24 permutations of the yods in their rows.
The number of permutations in the five sides of the two joined, Type A triangles = 5×24 = 120
= 22 + 42 + 62 + 82. The second & third
rows in each tetractys have (2+6=8) permutations (see diagram). Each Type A triangle has (3×8=24)
permutations of these rows. Hence, the 168 permutations comprise seven sets of 24
permutations. This is highly significant because Article 53 shows that the parameter 240 embodied in sacred geometries
divides into 72 and 168, where 72 is three sets
of 24 objects or geometrical elements and 168 is seven sets of 24 objects or elements.
This manifests in the subquark state of the E8×E8 heterotic superstring as the 24
E8 gauge charges spread along each of its 10 whorls (72 charges are
spread along its three major whorls and 168 gauges are spread along its seven minor
whorls). The same pattern exists in the tetractyses making up two joined Type A triangles as the seven sets
of 24 permutations of the yods in their rows.
The 35 rows in two joined, Type A hexagons have 360 (=36×10) permutations, where 36 is the number value of ELOHA, the Godname of Geburah. The 18 rows in each hexagon have 192 permutations made up of the 24 permutations of the four yods in the root edge and 168 permutations of the 17 rows outside it. They comprise the (5×24=120) permutations of the yods in the five sides of each hexagon outside the root edge and the 48 permutations (eight per sector) of the second & third rows. The latter form two sets of 24 permutations, namely, the 24 permutations in three sectors and the 24 permutations in the three sectors diametrically opposite them. Hence, the 168 permutations form seven sets of 24. The 360 permutations in the two joined hexagrams comprise (7+1+7=15) sets of 24.
| << Previous 1... 66 67 [68] 69 70 ...81 Next >> |