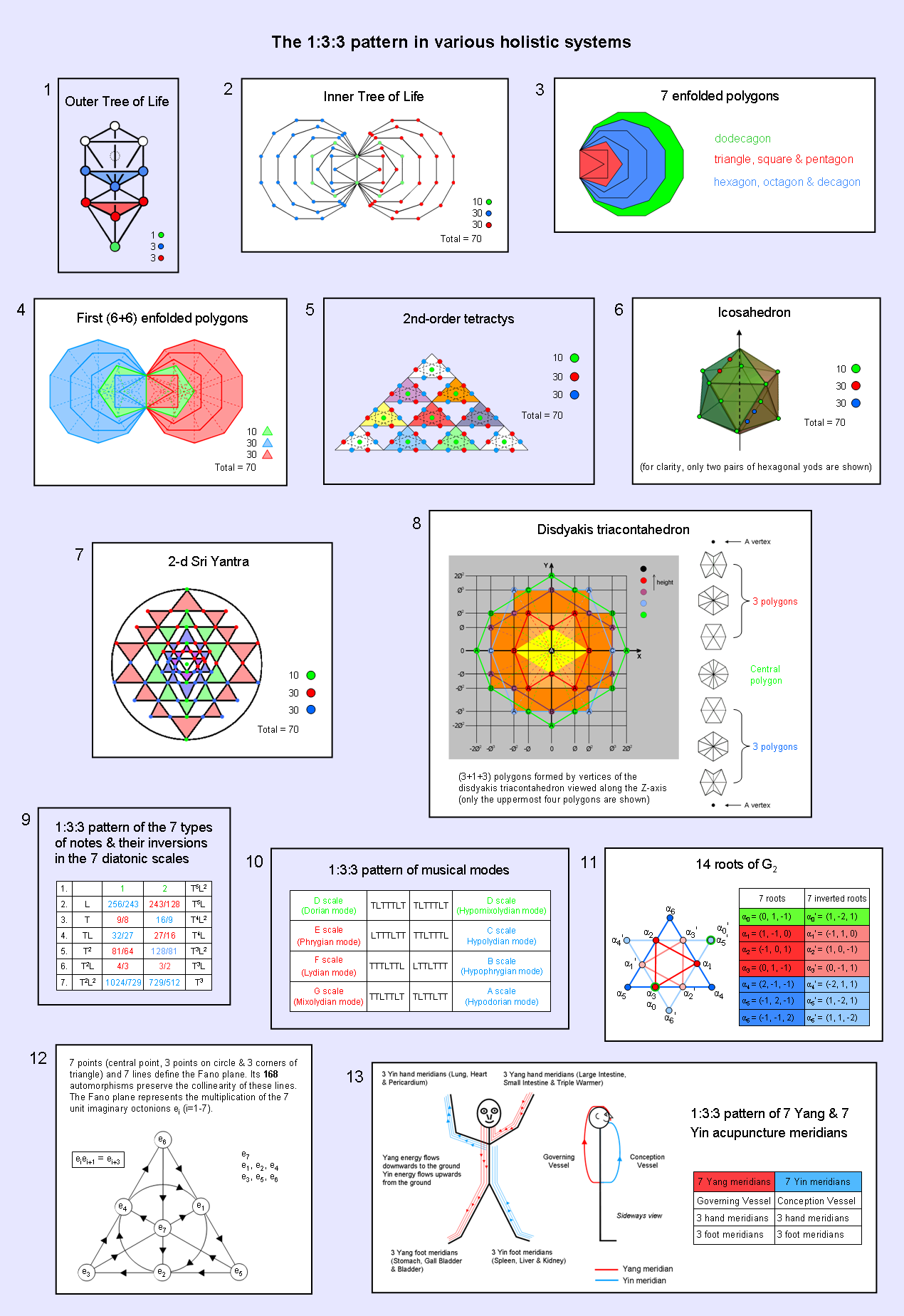
#65 The 1:3:3 pattern in sacred geometries and holistic systems

1. The seven Sephiroth of Construction of the outer Tree of Life consist of Malkuth (the outer, physical form of whatever conforms to this cosmic blueprint) and two triads:

Chesed-Geburah-Tiphareth (blue)
Netzach-Hod-Yesod (red)

2. The inner form of the Tree of Life consists of two sets of seven regular polygons enfolded in one another and sharing the same root edge:

triangle, square, pentagon, hexagon, octagon, decagon & dodecagon.

One set is the mirror image of the other set. The (7+7) enfolded polygons have 70 corners. They comprise:

• 10 green corners of the pair of hexagons (the fourth regular polygon);
• 30 red corners of the remaining polygons in one set;
• 30 blue corners of the remaining polygons in the other set.

3. The seven types of regular polygons in the inner Tree of Life comprise:

• the green dodecagon (the last polygon) with 12 corners;
• triplet of red polygons
  The triangle, square & pentagon have, respectively, 3, 4 & 5 corners.
• triplet of blue polygons
  The hexagon, octagon and decagon have, respectively, 6, 8 & 10 corners;

4. The first six enfolded polygons have 35 sectors. The first (6+6) enfolded polygons have 70 sectors. They comprise:

• the 10 green sectors of the two pentagons;
• the 30 red sectors of the triangle, square, hexagon, octagon & decagon in one set;
• the 30 blue sectors of the triangle, square, hexagon, octagon & decagon in the other set.

5. The 2nd-order tetractys consists of 10 1st-order tetractyses with 85 yods, where

85 = 4⁰ + 4¹ + 4² + 4³.

They comprise 15 corners, where

15 = 2⁰ + 2¹ + 2² + 2³,

and 70 hexagonal yods, which consist of:

• 10 green hexagonal yods at the centres of 1st-order tetractyses;
• 30 red hexagonal yods at the corners of 10 triangles;
• 30 blue hexagonal yods at the corners of triangles intersecting with the other 10 triangles to form Stars of David.

6. The fourth Platonic solid is the icosahedron with 12 vertices, 30 edges and 20 triangular faces. When the latter are tetractyses, an axis joining two opposite vertices is surrounded by:

• 10 green yods located at vertices;
• 30 red hexagonal yods on the 15 edges in one half of the polyhedron;
• 30 blue hexagonal yods on the 15 edges in its other half.

7. Including the central bindu, the 2-dimensional Sri Yantra consists of 70 points joined by 129 straight lines. They consist of:

• 10 green points lie on the central vertical axis;
• 30 red corners of triangles in one half of the Sri Yantra outside this axis;
• 30 blue corners of triangles in the other half outside this axis.

8. The disdyakis triacontahedron is the Catalan solid with the most faces. It has 62 vertices (three types: A, B & C), 180 edges & 120 triangular faces. The 60 vertices that surround an axis passing through two opposite A vertices are the corners of seven polygons that are perpendicular to this axis. They consist of:

• a central 12-gon;
• three polygons with 24 corners above the central 12-gon;
• three polygons with 24 corners below the central 12-gon (not shown in the diagram).

9. The octaves of the seven diatonic scales with tone ratios between 1 and 2 are composed of 14 types of notes:

(Red tone ratios denote Pythagorean notes and blue tone ratios denote non-Pythagorean notes). The first seven notes with tone ratios 1–1024/729 are followed by their inversions* 729/512–2. The former consist of:

• the tonic, or starting note (1);
• three Pythagorean notes (9/8, 81/64, 4/3);
• three non-Pythagorean notes (256/243, 32/27, 1024/729).

The latter comprise:

• the octave, or last note (2);
• three Pythagorean notes (3/2, 27/16, 243/128);
• three non-Pythagorean notes (729/512, 128/81, 16/9).

* The inversion of a note with tone ratio n is the note with tone ratio 2/n.

10. The eight Church modes consist of four authentic modes (Dorian, Phrygian, Lydian & Mixolydian) and four plagal modes (Hypodorian, Hypophrygian, Hypolydian & Hypomixolydian). They constitute seven musical scales, the Hypomixolydian mode being the same D scale as the Dorian but with a different dominant, or reciting note, and a different finalis, or ending note. The D scale is unique in that its sequence of intervals TLTTTLT is its own mirror image. The mirror image of the E scale is the C (Pythagorean) scale, the mirror image of the F scale is the B scale and the mirror image of the G scale is the A scale. This means that the seven types of diatonic scales consist of:

• D scale (mirror symmetric);
• E scale;
• F scale;
• G scale;

and the mirror images of the last three scales:

• C scale (mirror image of E scale);
• B scale (mirror image of F scale);
• A scale (mirror image of G scale).

11. The rank-2 exceptional Lie group G₂ with dimension 14 is the smallest of the five exceptional Lie groups. It has 14 roots, each being represented by a root vector with three Cartesian coordinates. They comprise two simple roots: α₀ & α₀′, and 12 roots: α₁–α₆  & their mirror images α₁′–α₆′. The former are located at the corners of two triangles — a dark red, smaller triangle & a dark blue, larger triangle. The latter are located at the corners of two triangles — a light red, smaller triangle & a light blue, larger triangle. The four triangles form two Stars of David. The two simple roots α₀ & α₀′ are located at, respectively, α₃ and α₅′. This is indicated in the diagram by the green rings around one dark red corner and one light red corner of the two smaller triangles. The 14 roots consist of the seven roots α₀–α₇ and their mirror images α₀′–α₇′. The former comprise:

• the simple root α₀ located at the position of α₃;
• three roots (α₁, α₂, α₃) represented by the three dark red corners of a small, dark red triangle;
• three roots (α₄, α₅, α₆) represented by the three dark blue corners of a larger, dark blue triangle.

The latter comprise:

• the simple root α₀′ located at the position of α₅′;
• three roots (α₁′, α₂′, α₃′) represented by the three light red corners of a second small, light red triangle;
• three roots (α₄′, α₅′, α₆′) represented by the three light blue corners of a second larger, light blue triangle. 

12. The Fano plane with order 2 and with 168 automorphisms preserving collinearity of points is the simplest finite projective plane. It consists of seven points and seven lines. Every point is on three lines and every line joins three points. The seven points consist of:

• a point at the centre of two triangles;
• a triplet of points at the corners of one of these triangles;
• a triplet of points at the corners of the other triangle.

The seven lines consist of:

• a central circle;
• three sides of a triangle;
• the three meridians of this triangle.

G₂ is the group of 168 automorphisms of the seven unit imaginary octonions e_i (e_i² = −1; i = 1–7). Their multiplicative algebra (e_ie_i+1 = e_i+3) is represented by the Fano plane if they are assigned to its seven points in the way that is shown in the diagram.

13. The 14 acupuncture meridians consist of seven meridians through which chi energy with Yang polarity flows and seven meridians with Yin chi energy. The seven Yang meridians are:

• Governing Vessel;
• three hand meridians (Large Intestine, Small Intestine, Triple Heater);
• three foot meridians (Gallbladder, Stomach, Bladder).

The seven Yin meridians are:

• Conception Vessel;
• three hand meridians (Lung, Heart, Pericardium);
• three foot meridians (Spleen, Kidneys, Liver).

These thirteen examples demonstrate that a 1:3:3 pattern (or, equivalently, a 10:30:30 pattern) is characteristic of holistic systems.

A high-resolution PDF version of the diagram is available here.

<< Previous    1...   63  64  [65]  66  67  ...81    Next >>

Home