| << Previous 1... 24 25 [26] 27 28 ...39 Next >> |
#26 Properties of the three types of regular polygons absent from the inner Tree of Life
(see also Article 58, Article 59 & the section The polygonal Godhead)

The inner Tree of Life comprises two sets of seven enfolded, regular polygons, one set being the mirror image of the other:
triangle, square, pentagon, hexagon, octagon, decagon & dodecagon.
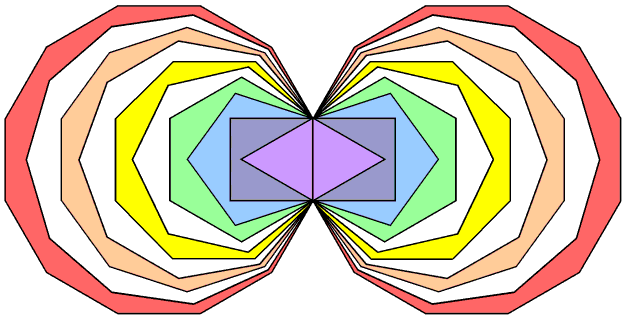
The dodecagon is the tenth regular polygon, so that three regular polygons are absent from the inner Tree of Life, namely, the 7-sided heptagon, the 9-sided nonagon & the 11-sided undecagon. They are shown coloured white in the adjacent diagram, the seven other types of polygons comprising the inner Tree of Life being coloured the seven colours of the rainbow. This absence suggests the following analogy between the first 10 regular polygons and the 10 Sephiroth of the Tree of Life:
Despite the fact that the geometry of overlapping circles generating the inner Tree of Life (see here) does not create three of the first 10 regular polygons, if this analogy between Sephiroth and polygons really holds, these absent polygons, being analogous to the Supernal Triad as the archetypal source of all levels of existence, might be expected to have properties analogous to those found in the seven types of polygons. Let us now investigate whether this is true.
The number of corners of the n sectors of an n-gon = n + 1, where "1" denotes its centre. The separate heptagon (n=7), nonagon (n=9) & undecagon (n=11) have 27 sectors with 30 corners. Enfolded and sharing the same side, they have (30−2−2=26) corners. The two joined, mirror-image sets of three polygons have 50 corners, where 26 is the number value of YAHWEH, the Godname of Chokmah, and 50 is the number value of ELOHIM, the Godname of Binah. These two Sephiroth head the Pillars, respectively, of Mercy and Judgement in the Tree of Life. As such, their Godnames prescribe the geometry of the three absent polygons in the simplest possible way. The seven separate polygons of the inner Tree of Life have 48 sectors with (48+7=55) corners, where 55 is the tenth triangular number:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.
The first 10 polygons are shown below arranged in a tetractys, the numbers denoting their corners. As they are analogous to the three Sephiroth of the Supernal Triad, the three absent polygons are located at the corners of the tetractys. The dodecagon occupies its centre because, as the last of the polygons making up the inner Tree of Life, it corresponds to Malkuth, the final Sephirah of Construction. The two triplets of polygons: (triangle, square, pentagon) & (hexagon, octagon, decagon) correspond to the two triads of Sephiroth of Construction: Chesed-Geburah-Tiphareth & Netzach-Hod-Yesod. The 10 separate polygons have (27+48=75) sectors with (30+55=85) corners. This is the number of yods making up the 10 tetractyses in a 2nd-order tetractys:
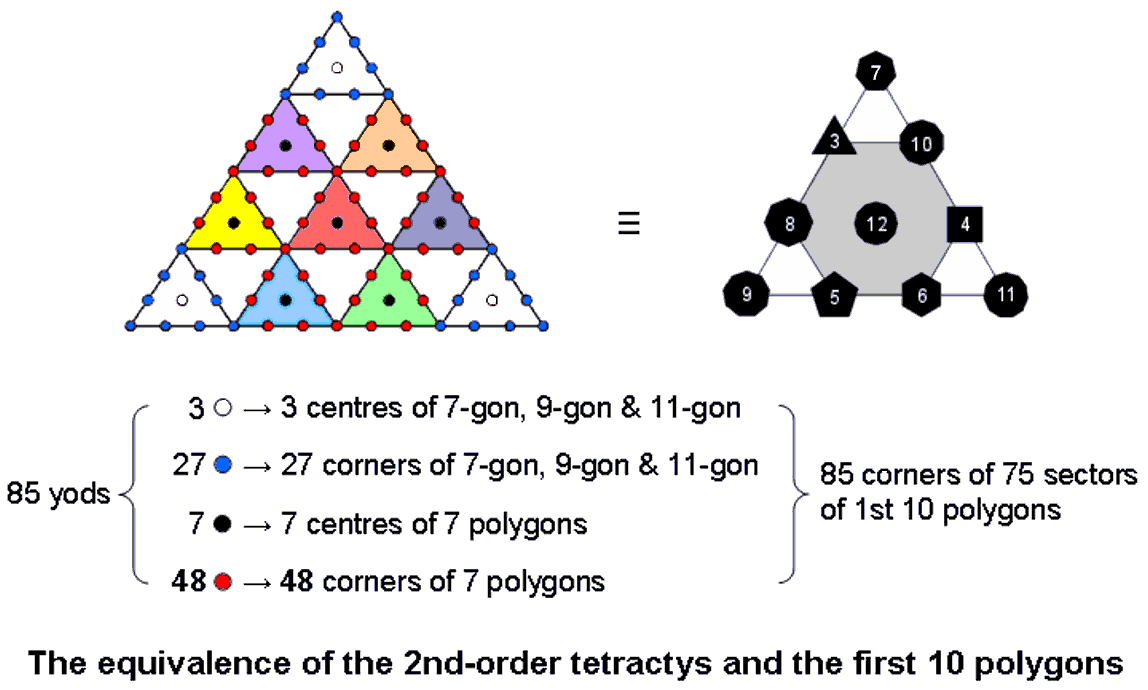 |
Moreover, the tetractyses at its three corners contain 30 yods, the seven other tetractyses containing 55 yods. The former are analogous to the 30 corners of the 27 sectors of the three absent polygons and the latter are analogous to the 55 corners of the 48 sectors of the seven polygons in the inner Tree of Life. The white centres of the three corner tetractyses correspond to the centres of the three absent polygons, their 27 blue yods correspond to the 27 corners of the latter, the seven black centres of the seven coloured tetractyses correspond to the centres of the seven polygons and their 48 red yods correspond to the 48 corners of these polygons (the six red corners of tetractyses correspond to the six corners of the hexagon and the 42 red hexagonal yods correspond to the 42 corners of the six other polygons). We see from these detailed correspondences that the 2nd-order tetractys symbolizes the first 10 polygons, with that part of it corresponding to the Supernal Triad symbolizing the three absent polygons and that part corresponding to the seven Sephiroth of Construction symbolizing the seven types of polygons in the inner Tree of Life. Here is mathematical confirmation that an analogy between the 10 Sephiroth of the Tree of Life and the first 10 types of polygons does, indeed, exist; there are far too many correspondences to be attributable, plausibly, to chance.
Tabulated below in Table 1 are the geometrical compositions of the 10 Type A polygons, the three absent Type A polygons and the seven Type A polygons of the inner Tree of Life (numbers in brackets refer to both sets):
|
Table 1. Geometrical compositions of the first 10 Type A polygons. |
|
10 polygons |
3 absent polygons |
7 polygons |
||||
| separate | enfolded | separate | enfolded | separate | enfolded | |
| Number of corners of sectors (C) | 85 (170) | 65 (128) | 30 (60) | 26 (50) | 55 (110) | 41 (80) |
| Number of sides of sectors (S) | 150 (300) | 139 (277) | 54 (108) | 52 (103) | 96 (192) | 88 (175) |
| Number of sectors (T) | 75 (150) | 74 (148) | 27 (54) | 27 (54) | 48 (96) | 47 (94) |
| Number of geometrical elements | 310 (620) | 278 (553) | 111 (222) | 105 (207) | 199 (398) | 176 (349) |
Comments
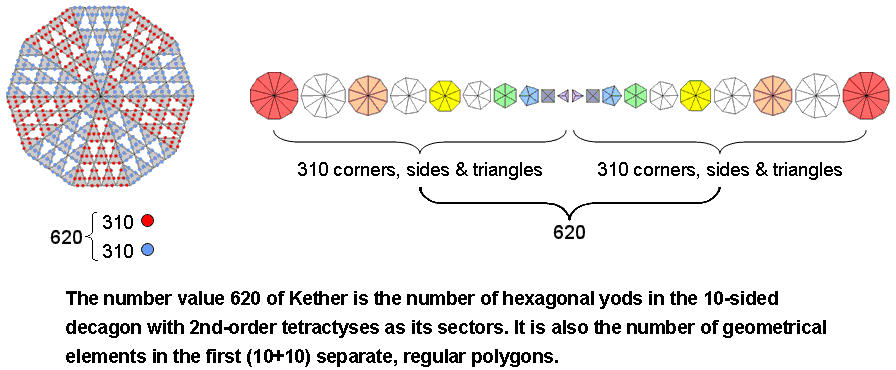
1. The Godname EL (אל) of Chesed with number value (1+30=31) prescribes the geometrical composition of the 10 separate polygons because they have 310 (=31×10) corners, sides & triangles. The value 1 of the letter alef (א) denotes the 10 centres and the value 30 of the letter lamed (ל) determines the 300 corners, sides & triangles that surround them. Both sets of 10 separate polygons have 620 geometrical elements, where 620 is the number of Kether ("Crown"):
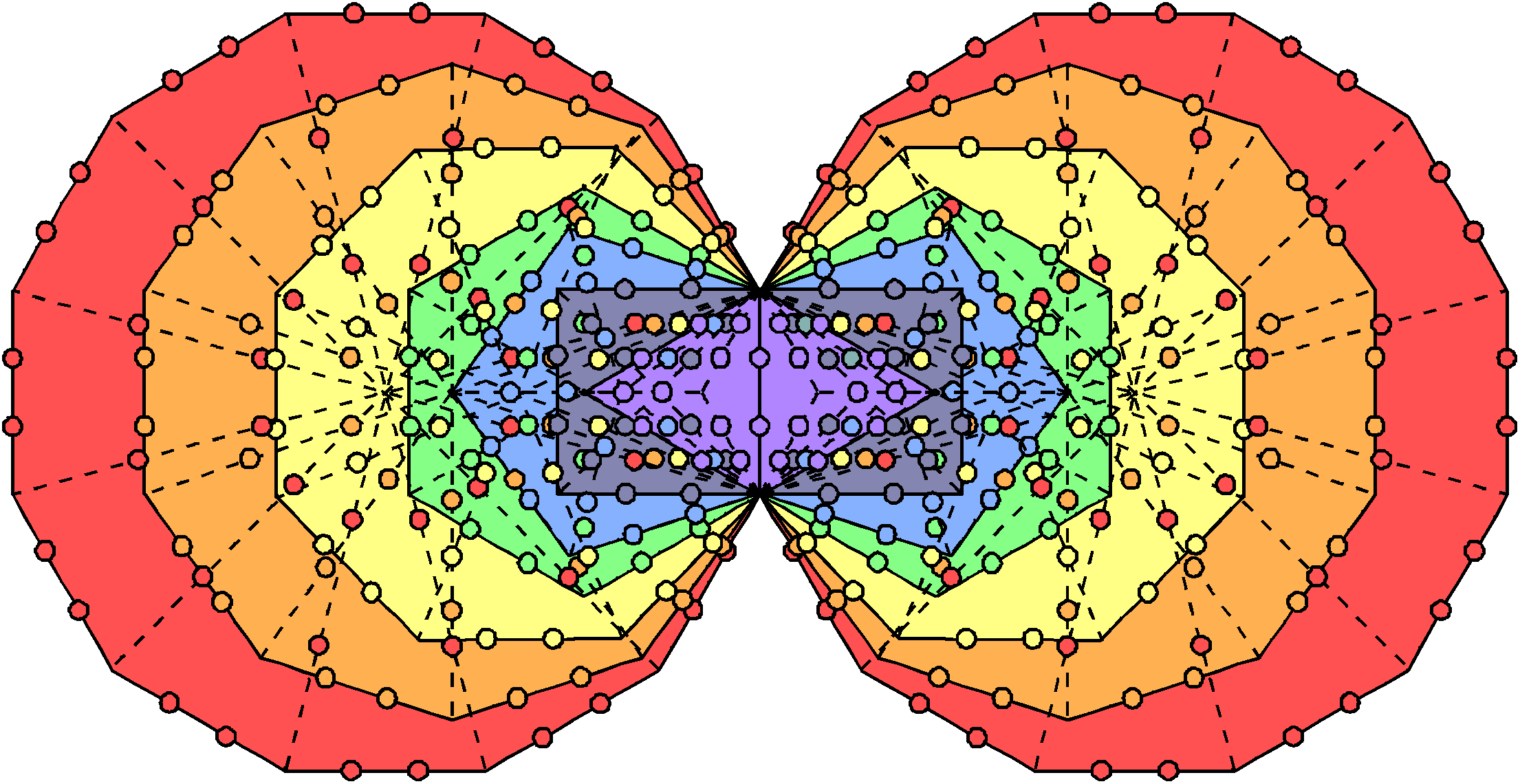
2. The first (10+10) enfolded polygons have 553 geometrical elements, i.e., 550 elements are outside their shared side, which possesses three elements. This is remarkable for two reasons: 1. 550 = 10(1+2+3+4+5+6+7+8+9+10), i.e., the Decad determines the geometrical composition of the first (10+10) enfolded polygons; 2. the number of SLs in the Cosmic Tree of Life is 550 (see here). Embodied, therefore, in the geometrical composition of the first (10+10) enfolded polygons is CTOL! It is the polygonal counterpart of the 550 geometrical elements in the faces of the five Platonic solids (see here);
3. The 74 sectors of the first 10 enfolded polygons:
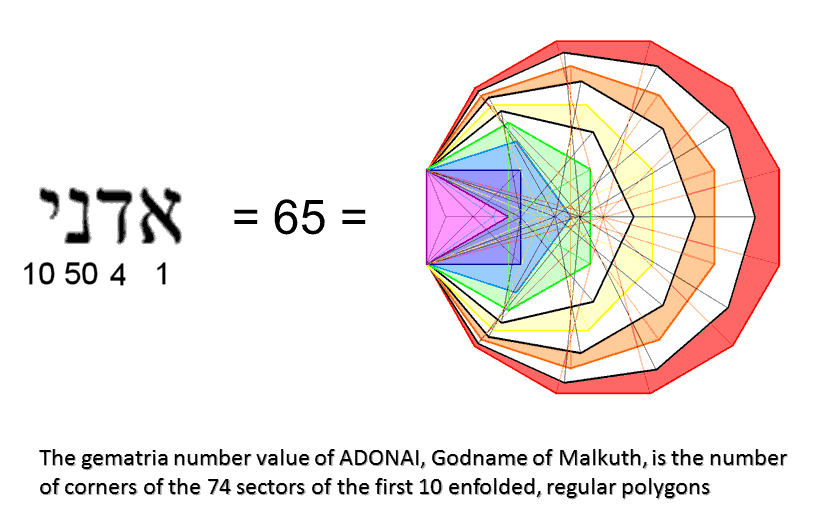
(the white sectors of the three absent polygons have black sides) have 65 corners, where 65 is the number of ADONAI (אדני), the Godname of Malkuth, and the sum of the first 10 integers after 1:
| 2 | ||||
| 3 | 4 | |||
| 65 = | 5 | 6 | 7 | |
| 8 | 9 | 10 | 11 . |
ADONAI prescribes the lowest 10 overlapping Trees of Life because they have 65 SLs (see here). It is therefore highly appropriate that this Godname, which is assigned to the Sephirah denoting the outer, material form of the Tree of Life, should determine the geometrical shape of the first 10 enfolded polygons marked out by the 65 corners of their 74 sectors. They also have 65 sides outside their shared side. Both sets of 10 enfolded polygons have (65+1+65=131) sides, where 131 is the number value of Samael, the Archangel of Geburah. The sectors of the 10 enfolded polygons have 139 sides. Remarkably, this is the number of yods in the first five enfolded polygons that make up the inner Tree of Life:
The first 10 enfolded polygons are shaped by 138 straight lines extending on either side of their shared side. This number is embodied in the Tetrahedral Lambda as the sum of the 10 integers (coloured red) arranged on the three sloping edges of the tetrahedral array of 20 integers:
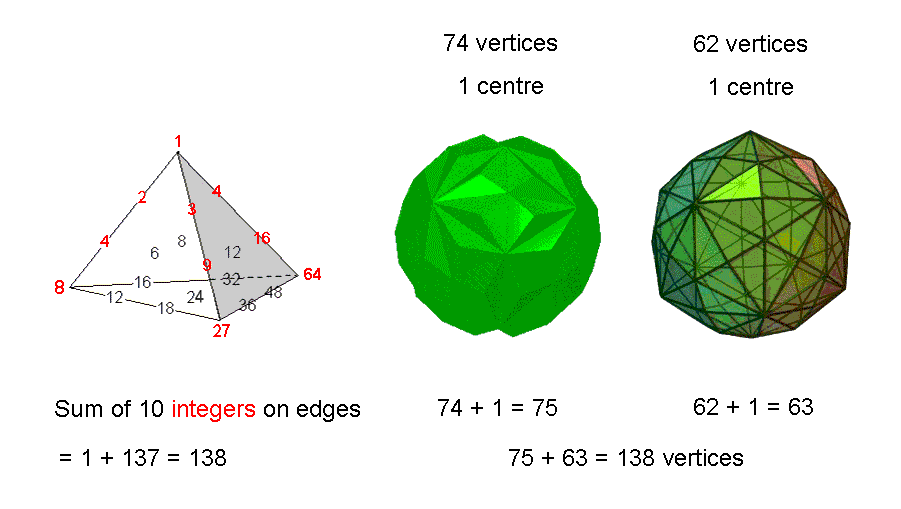
(integers at centres of faces are omitted for the sake of clarity). If the vertices of the two polyhedra making up the Polyhedral Tree of Life are joined to their centres, their resulting 396 internal triangles have 138 corners.
4. The 27 sectors of the three separate, absent polygons have (30+54=84) corners & sides, so that the 54 sectors in both sets of these polygons have 168 corners & sides:
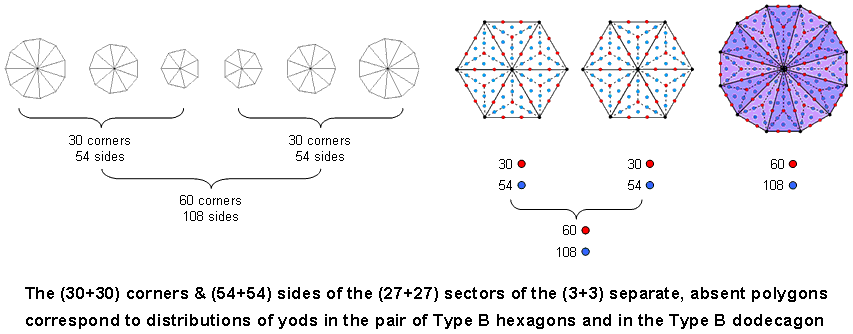
Their shapes are determined by the number of Cholem Yesodoth, the Mundane Chakra of Malkuth. Here is how the geometry of the three absent polygons embody the number that determines the structure of each of the 10 toroidal vortices making up a subquark superstring, namely, the 168 turns in one revolution of a helical whorl of the UPA. It is so plain and intuitively natural that it leaves no doubt about the archetypal nature of this geometry. It is reproduced in the pair of separate, Type B hexagons and in the Type B dodecagon as the (84+84=168) yods needed to transform their sectors into Type A triangles. Their (30+30) corners are symbolised by the (30+30) red yods in the tetractys sectors and their (54+54) sides are symbolised by the (54+54) blue yods added by converting the sectors into Type A triangles. Enfolded, the (3+3) separate, absent polygons have (50+103=153) corners & sides, where 153 is the number value of ELOHIM SABAOTH. The Godname ELOHIM with number value 50 prescribes their 50 corners and SABAOTH with number value 103 prescribes their 103 sides. The division of these 50 corners into the two endpoints of the shared side and the (24+24=48) corners outside it is characteristic of holistic systems (see here);
5. The (3+3) separate, absent polygons have 222 geometrical elements. This is the number of hexagonal yods associated with each set of seven enfolded polygons when their 47 sectors are tetractyses:
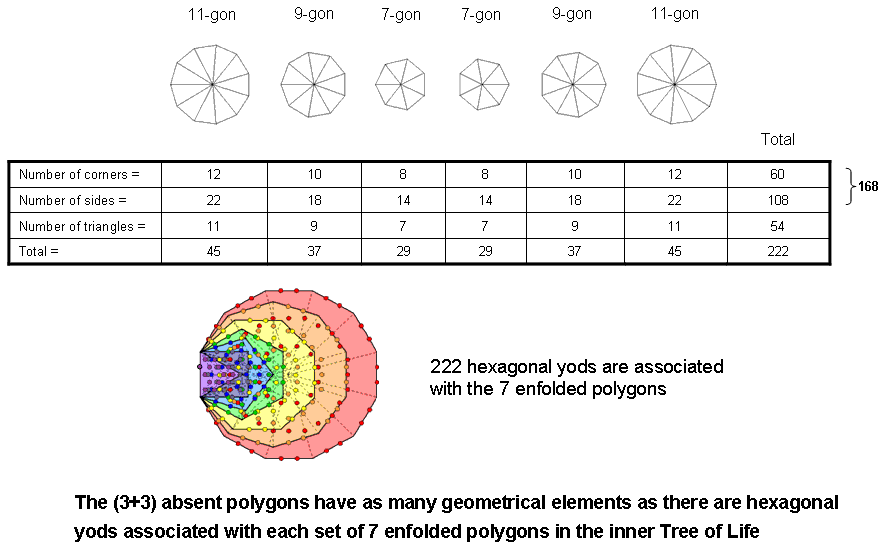
(See also #12). It is also the number of permutations of the rows of yods in the three orientations of a tetractys (see here). Notice that each orientation generates 74 permutations of the three rows of yods, where 74 is the number of sectors of the 10 enfolded polygons. This is also the number of vertices in the "144 Polyhedron" (see second diagram in comment (3)).
6. The 10 enfolded polygons have 55 corners that do not coincide with centres of polygons, where 55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10:
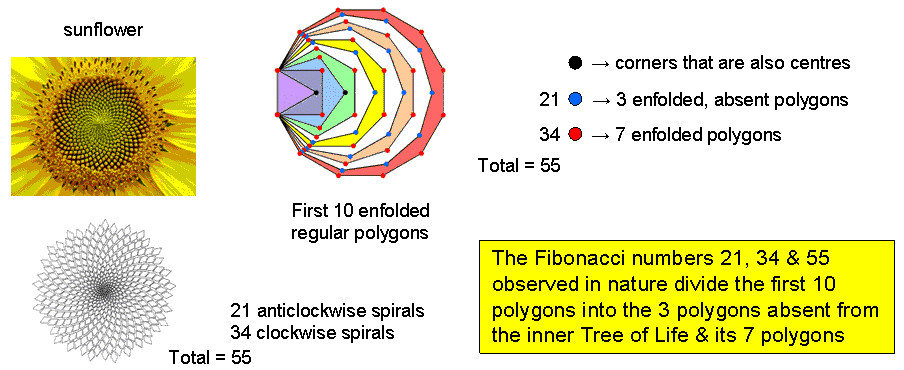
The three enfolded, absent polygons have 21 corners outside their shared side and the seven enfolded polygons of the inner Tree of Life have 34 corners that are not also centres. 21, 34 & 55 are three, successive members of the Fibonacci series that governs the growth patterns of many living things:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ....
The 3:7 division of polygons therefore corresponds to the difference between the anticlockwise and clockwise spiral patterns of florets in the sunflower. See Article 50 (Part 1) & Article 50 (Part 2) for how Fibonacci numbers manifest in various sacred geometries.
Tabulated below are the yod populations of the first 10 polygons, the three absent polygons and the seven polygons of the inner Tree of Life when constructed from tetractyses (numbers in brackets refer in each case to both sets):
|
10 polygons |
3 absent polygons |
7 polygons |
||||
| separate | enfolded | separate | enfolded | separate | enfolded | |
| Number of corners of sectors = C | 85 (170) | 65 (128) | 30 (60) | 26 (50) | 55 (110) | 41 (80) |
| Number of hexagonal yods = 2S + T | 375 (750) | 352 (702) | 135 (270) | 131 (260) | 240 (480) | 223 (444) |
| Number of yods on sides of tetractyses = C + 2S | 385 (770) | 343 (682) | 138 (276) | 130 (256) | 247 (494) | 217 (430) |
| Number of yods = C + 2S + T | 460 (920) | 417 (830) | 165 (330) | 157 (310) | 295 (590) | 264 (524) |
Comments
1. The first 10 enfolded polygons have 352 hexagonal yods, i.e., 350 hexagonal yods outside their shared side. This is both the number of hexagonal yods on the sides of the 94 tetractyses making up the (7+7) enfolded polygons and the sum of the 20 integers in the Tetrahedral Lambda (see Fig. 7 here). Their possession of the holistic parameter 350 is an indication of the archetypal character of the first 10 enfolded polygons. There are 351 hexagonal yods associated with each set of 10 enfolded polygons, where
351 = 1 + 2 + 3 +... + 26
(26th triangular number) is the number value of Ashim, the Order of Angels assigned to Malkuth. This shows in a very clear, undeniable way how YAHWEH, the Godname of Chokmah with number value 26, prescribes the hexagonal yod population of the 10 enfolded polygons. It also prescribes the 26 corners of the three enfolded, absent polygons. Indeed, there are 73 yods on their sides, where 73 is the number of Chokmah:
|
|
73 = |
|
|
|
|
|
Constructed from six tetractyses, a Star of David contains 73 yods. Furthermore, YAHWEH prescribes the hexagonal yod population of the (3+3) enfolded, absent polygons, which have 260 (=26×10) hexagonal yods. The three enfolded, absent polygons have 131 hexagonal yods, where 131 is the number value of Samael, the Archangel of Geburah. 129 hexagonal yods are outside their shared side, where 129 is the number value of YAHWEH SABAOTH, the Godname of Netzach. There are 702 hexagonal yods on the sides of the tetractyses in the (10+10) enfolded polygons. 350 (=35×10) hexagonal yods are distributed on either side of their shared root edge. This 35:35 division is characteristic of holistic systems, e.g., the 70 yods of the Tree of Life are composed of 35 yods in its trunk and 35 yods in its branches (see here). Amazingly, the (7+7) enfolded Type A polygons have 350 hexagonal yods on the 175 sides of their 94 tetractyses:
This demonstrates once again the holistic character of the first (10+10) polygons.
2. There are 385 yods on the sides of the 75 tetractys sectors of the first 10 separate polygons, where
385 = 12 + 22 + 32 + 42 + 52 + 62 + 72 + 82 + 92 + 102.

138 yods line the 54 sides of the 27 tetractys sectors of the three separate, absent polygons. Compare this with the fact discussed in (3) above that the 74 sectors of the 10 enfolded polygons have 138 sides outside their shared side. The same number measures the yods outside the shared side of two joined, Type A dodecagons (the last of the seven types of polygons of the inner Tree of Life). The Tetrad (4) determines the 256 yods lining the 54 tetractyses in the (3+3) enfolded, absent polygons because 256 = 44. This is striking evidence of how the Tetrad expresses properties of holistic systems;
3. The first 10 separate polygons contain 460 (=46×10) yods, where 46 is the number of yods in a Type B triangle. As the average yod population of the first 10 polygons, the number 46 is well-known in micro-biology as the number of chromosomes in the human cell. The first (10+10) separate polygons contain 920 yods, so that 900 (=90×10) yods surround their centres. The number 90 is the sum of the 10 integers in the Lambda Tetractys and is shown in many analyses on this website to be embodied in sacred geometries. Its manifestation here is no coincidence, of course, because of the holistic status of the first 10 polygons. The three separate, absent polygons contain 165 yods, where
165 = 12 + 32 + 52 + 72 + 92.
The three enfolded, absent polygons contain 157 yods, i.e., 153 yods outside their shared side, where 153 is the number value of ELOHIM SABAOTH, the Godname of Hod. The (3+3) enfolded, absent polygons contain (153+4+153=310 =31×10) yods, where 31 is the number value of EL, the Godname of Chesed. How appropriate that this Godname, which translates as "God," prescribes the yod population of those polygons that correspond to the Supernal Triad — the triple Godhead! How also appropriate that 155 yods are associated with each set of the three enfolded, absent polygons, for 155 is the number value of ADONAI MELEKH, the complete Godname of Malkuth! This number, truly, quantifies their form, in keeping with the meaning of Malkuth as the material form manifested by whatever holistic system conforms to the Tree of Life blueprint. Its geometrical representation is discussed in #11.
Listed below are the ways in which the Godnames of the 10 Sephiroth prescribe the three absent polygons — either separate or enfolded — that correspond to the three members of the Supernal Triad.
|
Sephirah |
Godname | Number value | ||
|
Kether |
EHYEH | 21 |  |
The (3+3) enfolded polygons have 44 corners. Each set of three enfolded polygons has 21 corners outside their shared side. |
| Chokmah | YAHWEH | 26 |  |
The 3 enfolded polygons have 27 sectors with 26 corners. |
| Binah | ELOHIM | 50 |  |
The (3+3) enfolded polygons have 54 sectors with 50 corners. |
|
Chesed |
EL | 31 | .png) |
The (3+3) enfolded polygons have 310 (=31×10) yods. |
|
Geburah |
ELOHA | 36 |  |
72 corners & sides outside their shared side surround the centres of the 3 enfolded polygons. 72 = 36th even integer. |
| Tiphareth | YAHWEH ELOHIM | 76 | .png)
|
Associated with each set of 3 enfolded polygons are 155 yods. 152 of these yods surround their centres. 152 = 76th even integer. |
|
Netzach |
YAHWEH SABAOTH | 129 |  |
129 hexagonal yods in 3 enfolded polygons are outside root edge. |
|
Hod |
ELOHIM SABAOTH | 153 |  |
The (3+3) enfolded polygons have 54 sectors with 50 corners & 103 sides, i.e., 153 corners & sides. 50 is the number value of ELOHIM and 103 is the number value of SABAOTH. |
.png) |
There are 153 yods in the 3 enfolded polygons outside their shared side. | |||
| Yesod | EL CHAI | 49 |  |
The (3+3) enfolded polygons have 49 sides. |
|
Malkuth |
ADONAI | 65 | .png) |
130 yods line the sides of the 27 sectors of the 3 enfolded polygons. 130 = 65th even integer. |
| ADONAI MELEKH | 155 | .png) |
155 yods are associated with each set of 3 enfolded polygons. |
Now consider the case where all the polygons are Type B:
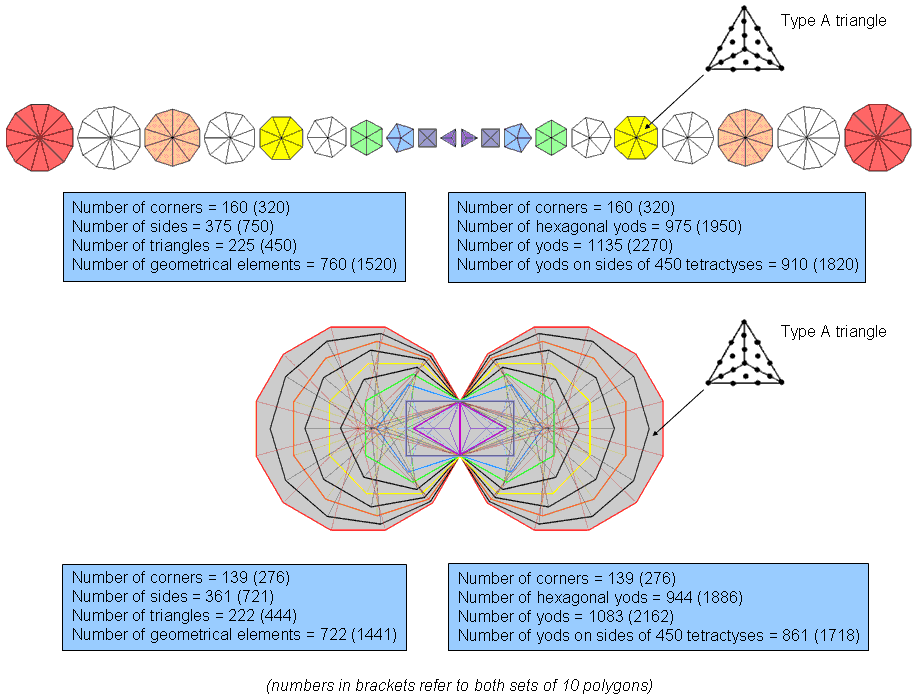
Tabulated below are the geometrical compositions of the 10 Type B polygons, the three absent Type B polygons and the seven Type B polygons of the inner Tree of Life (numbers in brackets refer to both sets):
|
10 polygons |
3 absent polygons |
7 polygons |
||||
| separate | enfolded | separate | enfolded | separate | enfolded | |
| Number of corners of sectors (C) | 160 (320) | 139 (276) | 57 (114) | 53 (104) | 103 (206) | 88 (174) |
| Number of sides of sectors (S) | 375 (750) | 361 (721) | 135 (270) | 133 (265) | 240 (480) | 229 (457) |
| Number of sectors (T) | 225 (450) | 222 (444) | 81 (162) | 81 (162) | 144 (288) | 141 (282) |
| Number of geometrical elements | 760 (1520) | 722 (1441) | 273 (546) | 267 (531) | 487 (974) | 458 (913) |
Comments
1. The 10 separate polygons have 760 (=76×10) geometrical elements. They are prescribed by YAHWEH ELOHIM, the Godname of Tiphareth with number value 76. (760−30=730=73×10) geometrical elements are outside the sides that become shared when they are enfolded, where 73 is the number value of Chokmah. The 10 enfolded polygons have 222 triangles with 139 corners, i.e., 137 corners outside their shared side determine their shapes, where 137 is the number whose reciprocal is, approximately, the fine-structure constant. Alternatively, as the topmost corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree of Life, 137 corners intrinsic to a set of 10 enfolded polygons are associated with each set. The latter are displayed below. Notice that there are no green circles at the tops of the two hexagons because these two corners are not intrinsic to the (10+10) enfolded polygons.
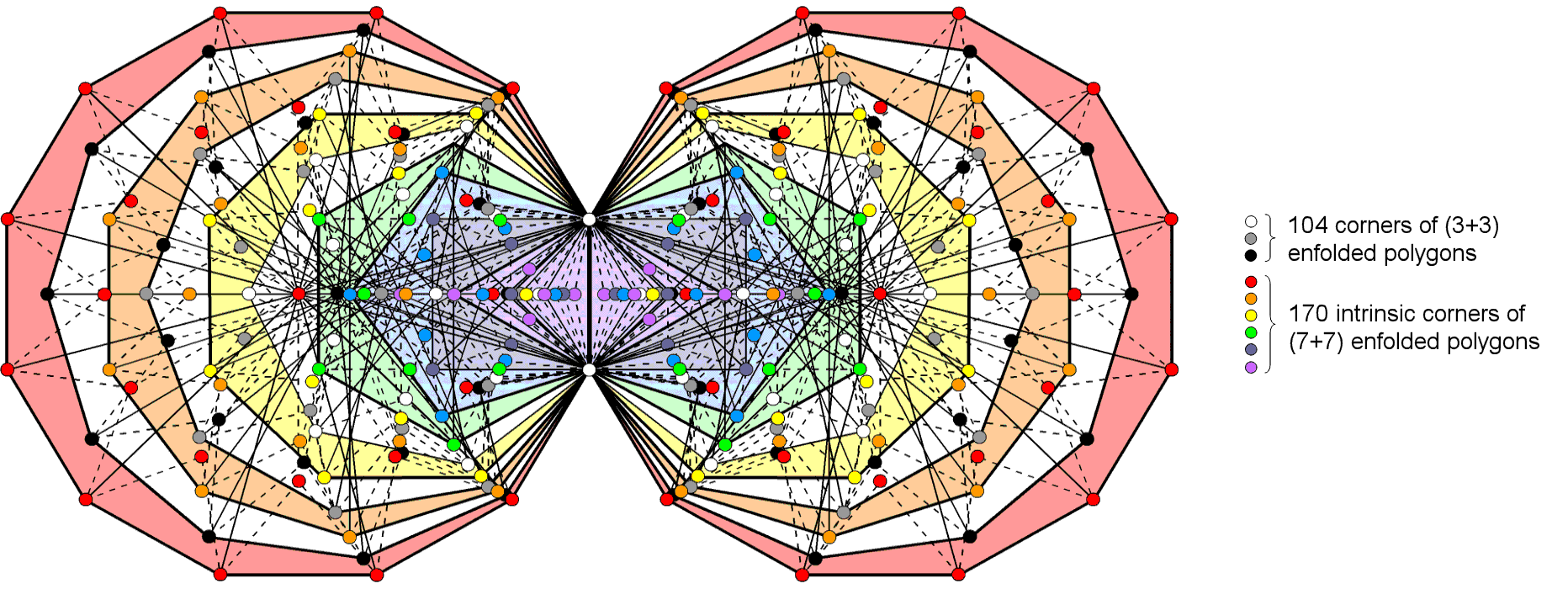
137 corners are intrinsic to each set of 10 enfolded polygons. 137 is the 33rd prime number, where 33 = 1! + 21 + 3! + 4!. It is one of the most mysterious numbers in physics.
So we see that the mysterious number 137 in physics that determines the size and properties of the atoms of the elements actually determines the skeletal form of the first 10 enfolded polygons! It appears in the (7+7) enfolded Type B polygons as their 1370 (=137×10) yods (see here). Enfolded, the first 10 polygons have 222 triangles with 361 sides, where 361 = 192, i.e., the square of the tenth odd integer. ELOHA, the Godname of Geburah with number value 36, determines the 360 (=36×10) sides outside their shared side;
2. The (10+10) enfolded polygons are composed of 444 triangles. This is the number of hexagonal yods in the (7+7) enfolded Type A polygons (see last diagram here). Symbolised, therefore, by the hexagonal yods in the inner form of the Tree of Life are the triangular sectors of the (10+10) enfolded Type B polygons;
3. The three enfolded polygons have 267 geometrical elements, i.e., 264 elements outside their shared side. This is the number of yods in the seven enfolded Type A polygons (see here);
4. The 10 enfolded polygons have 500 (=50×10) corners & sides. ELOHIM, the Godname of Binah with number value 50, prescribes their shape. As their shared side consists of two endpoints and one line, there are 497 corners & sides outside the root edge. In the context of overlapping Trees of Life where each Tree has its own set of (7+7) enfolded polygons, if we now consider the hidden (3+3) polygons accompanying each set, there are 496 geometrical elements that are intrinsic to each set of 10 enfolded polygons because — as was pointed out in comment 1 — the topmost corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree of Life and so it is not intrinsic to the set of 10 enfolded polygons because it is shared by the polygons enfolded in that Tree. The number 496 is the number value of Malkuth. Embodied in the 10 enfolded polygons is the dimension of SO(32) and E8×E8, the two gauge symmetry groups which permit interactions between superstrings that are free of quantum anomalies;
5. As the three enfolded polygons have 26 corners, there are (500−26=474) corners & sides other than these in the 10 enfolded polygons. 474 is the number of Daath (“knowledge”);
6. As the (10+10) enfolded polygons have 444 triangles with 276 corners, of which two corners are not intrinsic to these polygons, there are (276−2−2=272) corners outside the root edge that are intrinsic to these polygons. 272 is the number value of Cherubim, the Order of Angels that is assigned to Yesod, the ninth Sephirah.
Tabulated below are the yod populations of the 10 Type B polygons, the three absent Type B polygons and the seven Type B polygons of the inner Tree of Life (numbers in brackets refer in each case to both sets):
|
10 polygons |
3 absent polygons |
7 polygons |
||||
| separate | enfolded | separate | enfolded | separate | enfolded | |
| Number of corners of tetractyses = C | 160 (320) | 139 (276) | 57 (114) | 53 (104) | 103 (206) | 88 (174) |
| Number of hexagonal yods = 2S + T | 975 (1950) | 944 (1886) | 351 (702) | 347 (692) | 624 (1248) | 599 (1196) |
| Number of yods on sides of tetractyses = C + 2S | 910 (1820) | 861 (1718) | 327 (654) | 319 (634) | 583 (1166) | 546 (1088) |
| Number of yods = C + 2S + T | 1135 (2270) | 1083 (2162) | 408 (816) | 400 (796) | 727 (1454) | 687 (1370) |
Comments
1. YAHWEH with number value 26 prescribes the 351 hexagonal yods in the three separate, absent polygons because
351 = 1 + 2 + 3 + .... + 26,
i.e., 351 is the 26th triangular number;
2. There are 910 (=91×10) yods on the sides of the 225 tetractyses in the 10 separate polygons. Embodied in the number quantifying the boundaries of their tetractyses is the number (91) of Trees of Life in the Cosmic Tree of Life. The (10+10) separate polygons have 1820 such yods on the boundaries of their 450 tetractyses. Remarkably, this is the number of yods surrounding the centres of the five Platonic solids when their faces are constructed from tetractyses and their interior triangles meeting at their centres are Type A (see table here);
3. The number of yods in the (10+10) separate polygons = 2270 = 227×10. As 227 is the 49th prime number, this shows how EL ChAI, the Godname of Yesod with number value 49, prescribes the (10+10) separate polygons;
4. The number of yods in the (10+10) enfolded polygons = 2162 = 2×1081. Amazingly, the number value 1081 of Tiphareth ("Beauty") is the number of yods associated with each set of the first 10 enfolded polygons! As
1081 = 1 + 2 + 3 + ... + 46,
the simplest Type B polygon — the triangle — embodies this number arithmetically because it has 46 yods. It is remarkable that the number of Tiphareth should measure the yods associated with the 10 enfolded polygons, whilst the number of its Godname should measure the number of points, lines & triangles in the 10 separate polygons. It would be tantamount to believing in miracles to dismiss this as a coincidence. Instead, this property is an eloquent expression of the beautiful power and intelligence of genuine sacred geometries. It reveals the way in which the true meaning of the word 'sacred' transcends all cultural contexts, whatever religion in which these geometries originate (and even if it was inspired by no religion). There are 1088 yods on the sides of the 282 tetractyses in the (7+7) enfolded polygons. The topmost corners of the two hexagons coincide with the lowest corners of the hexagons enfolded in the next higher Tree of Life. Hence, 1086 boundary yods are intrinsic to each set of (7+7) enfolded polygons, i.e., 1082 intrinsic, boundary yods are outside the root edge. 1082 is the 1081st integer after 1, once again showing how the number of Tiphareth determines the shape of the inner Tree of Life;
5. The first 10 enfolded Type B polygons have 222 tetractys sectors with 139 corners, i.e., 137 corners outside their root edge. The number determining the fine-structure constant shapes the first 10 enfolded Type B polygons as the number of points marking out their corners outside their shared side. This property is analogous to the 139 yods in the first five enfolded polygons, shown earlier;
6. The first 10 enfolded polygons have 944 hexagonal yods. 222 of them are at the centres of the 222 tetractyses, leaving 722 hexagonal yods lining their sides. 720 of these are outside the root edge. Hence, (137+720=857) such yods line their sides. Including the four yods of the root edge, (4+857=861) yods line their sides. Surrounding the 10 centres of the polygons are 851 boundary yods. One of them (indicated by a white yod in the figure below on the left in the second row):
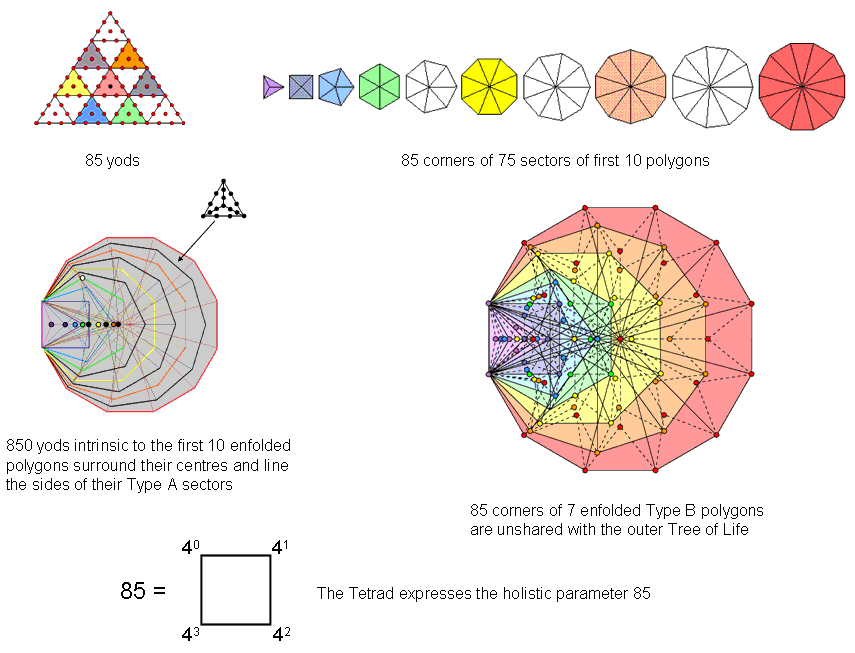
is the topmost corner of the green hexagon, which coincides with the lowest corner of the hexagon enfolded in the next higher Tree of Life. This is the only corner which is shared with polygons enfolded in the next higher Tree, so that 850 (=85×10) boundary yods intrinsic to the 10 polygons enfolded in any Tree of Life surround their centres. This demonstration that they embody the holistic parameter 85, which was encountered earlier as the 85 corners of the first 10 separate polygons is further evidence of their holistic character;
7. Of the 857 yods outside the root edge that line sides of 222 tetractyses, 24 yods are corners of the 27 sectors of the three types of polygons absent from the inner Tree of Life. (857−24=833) yods other than these corners line the sides of the tetractyses making up the 10 enfolded Type B polygons. 833 is the number value of Chaioth ha Qadesh (“Holy Living Creatures”), the Order of Angels assigned to Kether;
8. Of the 857 boundary yods outside the root edge, 21 yods are corners of the three enfolded polygons, where 21 is the number value of EHYEH, the Godname of Kether. (857−21=836) yods outside the root edge line tetractyses that are not corners of the three polygons that were hypothesized at the beginning of this article to correspond to Kether, Chokmah & Binah. Including the root edge, (836+4=840) yods other than these corners line sides of 222 tetractyses:
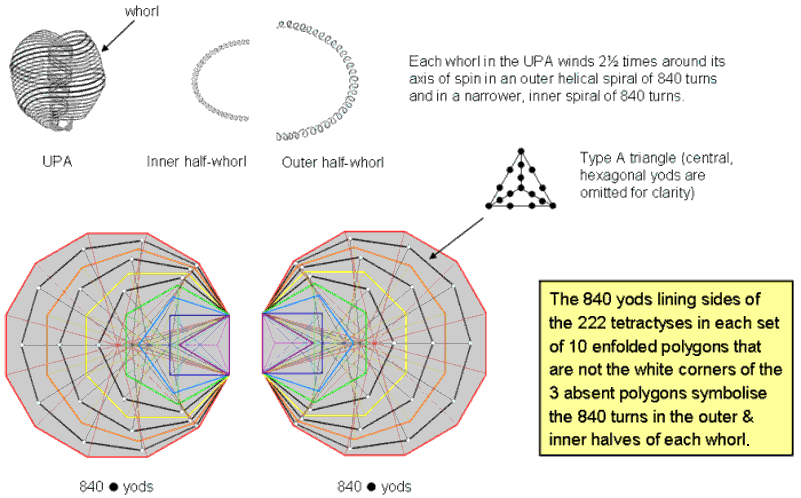
The 840 yods lining tetractyses in the 10 enfolded Type B polygons that are not corners of the three absent polygons symbolize the 840 turns in the outer & inner halves of each whorl of the UPA/subquark superstring.
Embodied in the 10 enfolded polygons is the superstring structural parameter 840 — the number of turns in an outer or inner half of each whorl of the UPA remote-viewed by Annie Besant & C.W. Leadbeater over a century ago and identified by the author as the subquark state of the E8×E8 heterotic superstring (see his books on this website). This property is the full expression of the 84 corners & sides of the three separate Type A polygons that are absent from the inner Tree of Life, as shown in comment 4 about the geometrical composition of the first 10 polygons tabulated in Table 1. Notice that the (21+21=42) corners of the (3+3) enfolded polygons outside their shared side play no part in determining this number. It is the geometrical realization of the fundamental, metaphysical dichotomy between the Supernal Triad, which exist outside all levels of reality, and the seven Sephiroth of Construction, which express these realities (actually, the seven cosmic planes of consciousness mapped by the Cosmic Tree of Life);
9. The (10+10) enfolded polygons contain 1886 hexagonal yods. According to Table 1, the 54 sectors of the (3+3) enfolded polygons have 103 sides, where 103 is the number of SABAOTH (“Hosts”), part of the Godnames of Hod & Netzach. 206 hexagonal yods line the sides of their sectors. Hence, (1886−206=1680) extra hexagonal yods are needed to turn the 148 sectors of the (10+10) enfolded Type A polygons into the 444 tetractyses making up the (10+10) Type B polygons. 1680 yods line the sides of the two separate sets of 10 enfolded Type B polygons and 1680 hexagonal yods (840 hexagonal yods in each set) have to added to the (3+3) enfolded Type A polygons in order to generate the (10+10) enfolded Type B polygons. This reveals how they embody the superstring structural parameter 1680. There are (148+10+10=168) corners inside the boundaries of all the polygons, showing how they embody the number of Cholem Yesodoth, the Mundane Chakra of Malkuth. The following, remarkable relationship emerges:
1886 hexagonal yods = 206 hexagonal yods + 1680 hexagonal yods.
|
|
|
Vortex ring |
The human skeleton has 206 bones and a helical whorl of the UPA/superstring has 1680 turns. It
is, of course, meaningless to add together such different entities as bones and polarised oscillations of
a vortex ring —
a component of the 10-fold superstring. However, this is not the point. It cannot
be regarded as merely a curious coincidence, for both numbers have definite
geometrical meanings in the context of the geometry of the first 10 polygons, namely, 206 hexagonal yods lining
sides of the 54 sectors of the
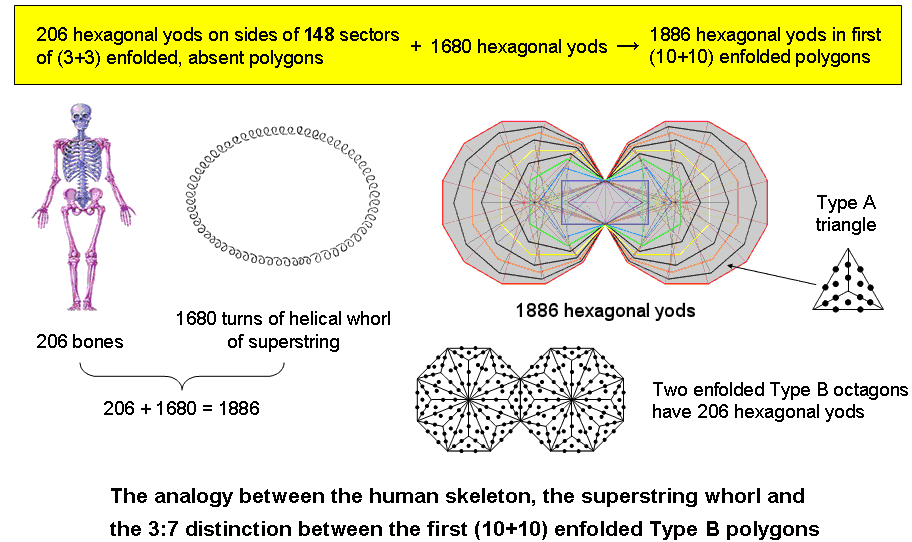
(3+3) enfolded Type A polygons absent from the inner Tree of Life and 1680 hexagonal yods added by the conversion of the (10+10) enfolded polygons into Type B polygons. The division stems from the basic distinction between the Supernal Triad (the triple Godhead) and the seven Sephiroth of Construction. What is remarkable is that the primary, structural parameters of the human body and the microscopic whorl should add up to the number of hexagonal yods in the (10+10) enfolded, Type B polygons! Holistic parameters can be composed of several other holistic parameters, each having its own context that is not necessarily inter-related. The number 206 is also embodied in the two enfolded, Type B octagons because they contain 206 hexagonal yods. This means that the other (9+9) enfolded polygons contain 1680 hexagonal yods, each set of nine polygons having 840 hexagonal yods outside their shared, root edge. As a Type A octagon contains 49 yods (see here), EL ChAI, the Godname of Yesod with number value 49, can be said to prescribe the 1680 circularly polarised oscillations in the vortex ring, or toroidal vortex, that is a whorl of the UPA/subquark superstring, for the polygons other than the two octagons contain 1680 hexagonal yods. As the Malkuth aspect of the microscopic and human Trees of Life, the 3-dimensional forms of the human skeleton and each whorl of the subquark superstring are separately embodied in the first (10+10) enfolded, Type B polygons.
| << Previous 1... 24 25 [26] 27 28 ...39 Next >> |