Article 59

ARTICLE 59

by

Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://smphillips.mysite.com

Abstract

Three types of polygons are absent from the seven regular polygons that make up the inner form of the Tree of Life. This 3:7 division manifests in the 10 Sephiroth of the outer Tree of Life as the three Sephiroth of the Supernal Triad denoting the subjective, triple aspect of the Godhead and the seven Sephiroth of Construction, which are the objective aspects of God. This article explores the possibility that the three absent polygons bear a formal correspondence to the Supernal Triad, just as the author long suspected that the seven types of polygons are analogous to the seven Sephiroth of Construction. Evidence for this correspondence is that the same archetypal pattern of numbers found in previous articles to characterise sacred geometries, including the seven polygons, occur also in the three absent polygons. One of these numbers is 248, which is the dimension of E₈, the rank-8 Lie group at the heart of superstring physics. It is the number of yods surrounding the centres of the (3+3) enfolded polygons that line the sides of their tetractys sectors outside their shared side. The number that determines the shapes of these sectors quantifies the forces that created all the forms of matter in the visible universe. Evidence that this is not mere coincidence is provided by the fact that the 248 yods naturally divide into eight yods corresponding to the eight simple roots of E₈ and 240 others that correspond to its non-zero roots. Furthermore, natural subsets of these yods correspond to the numbers of roots in its four exceptional subgroups. When regarded as Type B polygons, the (3+3) enfolded polygons contain, surrounding their centres and outside their shared side, (240+240) geometrical elements that are not corners. This is the counterpart of the (240+240) roots of E₈×E₈. The five external corners of each heptagon and the centres of each set of three polygons denote the eight simple roots of each E₈. The 240 geometrical elements in each set divide naturally into 10 sets of 24 elements (actually (3+7) sets). It confirms a similar property found in Article 53 for five sacred geometries. This (3+7)-fold pattern manifests in the three major whorls and seven minor whorls of the UPA, the basic unit of nuclear matter remote-viewed over a century ago by Annie Besant & C.W. Leadbeater and identified by the author as the subquark state of the 10-dimensional, E₈×E₈ heterotic superstring. What emerges is several forms of evidence — mathematical and historical — that the first 10 types of polygons constitute an archetypal set of relevance to superstring theory and the search for its generalisation in M-theory.

1

Table 1. Gematria number values of the ten Sephiroth in the four Worlds.

SEPHIRAH

GODNAME

ARCHANGEL

ORDER OF
ANGELS

MUNDANE
CHAKRA

1
Kether
(Crown)
620 EHYEH
(I am)
21 Metatron
(Angel of the
Presence)
314 Chaioth ha Qadesh
(Holy Living
Creatures)
833
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
636

2
Chokmah
(Wisdom)
73 YAHWEH, YAH
(The Lord)
26, 15
Raziel
(Herald of the
Deity)
248 Auphanim
(Wheels)
187 Masloth
(The Sphere of
the Zodiac)
140

3
Binah
(Understanding)
67 ELOHIM
(God in multiplicity)
50
Tzaphkiel
(Contemplation
of God)
311
Aralim
(Thrones)
282
Shabathai
Rest.
(Saturn)
317

Daath
(Knowledge)
474

4
Chesed
(Mercy)
72 EL
(God)
31 Tzadkiel
(Benevolence
of God)
62 Chasmalim
(Shining Ones)
428
Tzadekh
Righteousness.
(Jupiter)
194

5
Geburah
(Severity)
216
ELOHA
(The Almighty)
36
Samael
(Severity of God)
131
Seraphim
(Fiery Serpents)
630
Madim
Vehement Strength.
(Mars)
95

6
Tiphareth
(Beauty)
1081
YAHWEH ELOHIM
(God the Creator)
76 Michael
(Like unto God)
101
Malachim
(Kings)
140
Shemesh
The Solar Light.
(Sun)
640

7
Netzach
(Victory)
148
YAHWEH SABAOTH
(Lord of Hosts)
129
Haniel
(Grace of God)
97 Tarshishim or
Elohim
1260
Nogah
Glittering Splendour.
(Venus)
64

8
Hod
(Glory)
15
ELOHIM SABAOTH
(God of Hosts)
153
Raphael
(Divine Physician)
311
Beni Elohim
(Sons of God)
112
Kokab
The Stellar Light.
(Mercury)
48

9
Yesod
(Foundation)
80
SHADDAI EL CHAI
(Almighty Living
God)
49, 363
Gabriel
(Strong Man of
God)
246
Cherubim
(The Strong)
272
Levanah
The Lunar Flame.
(Moon)
87

10
Malkuth
(Kingdom)
496
ADONAI MELEKH
(The Lord and King)
65, 155
Sandalphon
(Manifest Messiah)
280 Ashim
(Souls of Fire)
351
Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168

The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters.

(Numbers in this table referred to in the article will be written in boldface).

2

1. Dimensional meaning of the 26 corners of the 3 enfolded, absent polygons

The 26 corners of the 27 sectors of the three enfolded polygons (the heptagon, nonagon & undecagon) that are absent from the seven types of polygons making up the inner Tree of Life denote the 26 dimensions of space-time predicted by quantum mechanics for spinless strings. They consist of the dimension of time, the three large-scale dimensions of space, the six compactified dimensions of the 10-dimensional space-time of superstrings and 16 higher dimensions, one of which is either a circular dimension (SO(32) or the segment or gap separating the two 10-dimensional space-time sheets containing heterotic superstrings of ordinary and shadow matter (E₈×E₈). The question arises: which dimensions correspond to which corners? The clue is provided by the fact that the 26 corners comprise the two endpoints of the root edge and 24 corners consisting of the three centres of the polygons and their 21 corners. This 3:21 division of the number 24 is characteristic of sacred geometries, e.g.,

1. the 24 corners of the first 6 enfolded polygons of the inner Tree of Life comprise a corner of the triangle and the top & bottom corners of the hexagon — the three corners that coincide with corners of triangles belonging to the outer Tree of Life — and 21 corners unshared with the latter;

2. 21 hexagonal yods are at the centres of the 21 triangles in each half of the Sri Yantra when they are tetractyses and three hexagonal yods on the sides of the central triangle are at the corners of each of two overlapping triangles.

The distribution of corners in the three enfolded polygons into those above and below the horizontal axis passing through their centres and three corners reveals that the 10 corners above or below this axis are composed of one, two, three & four corners:

Table 2. Numbers of corners in three enfolded polygons.

root edge
heptagon

nonagon

undecagon

Above axis 1 2 3 4

On axis
0 1 + 1 1 + 1 1 + 1

Below axis 1 2 3 4

This is the pattern of the numbers 1, 2, 3 & 4 symbolised by the four rows of the Pythagorean tetractys! As the number 21 of AHIH, the Godname of Kether:

1 + 5 + 10 + 5

refers to the 21 corners of the three polygons outside the root edge and the number 26 of YHVH, the Godname of Chokmah:

10 + 5 + 6 + 5

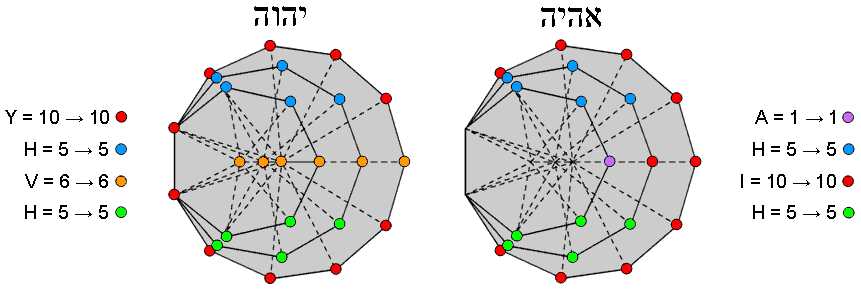
Figure 1. YAHWEH & EHYEH prescribe the three enfolded polygons that are absent from the inner Tree of Life.

refers to both these and the five extra corners that are either endpoints of the root edge or centres of the three polygons, the value 1 of A must refer to a corner of one of the

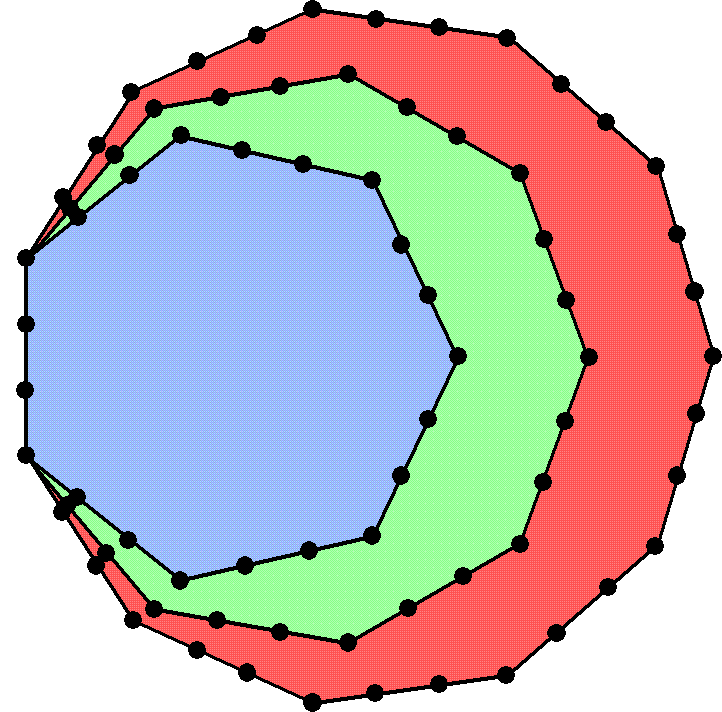
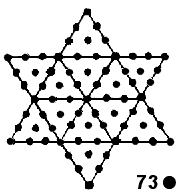
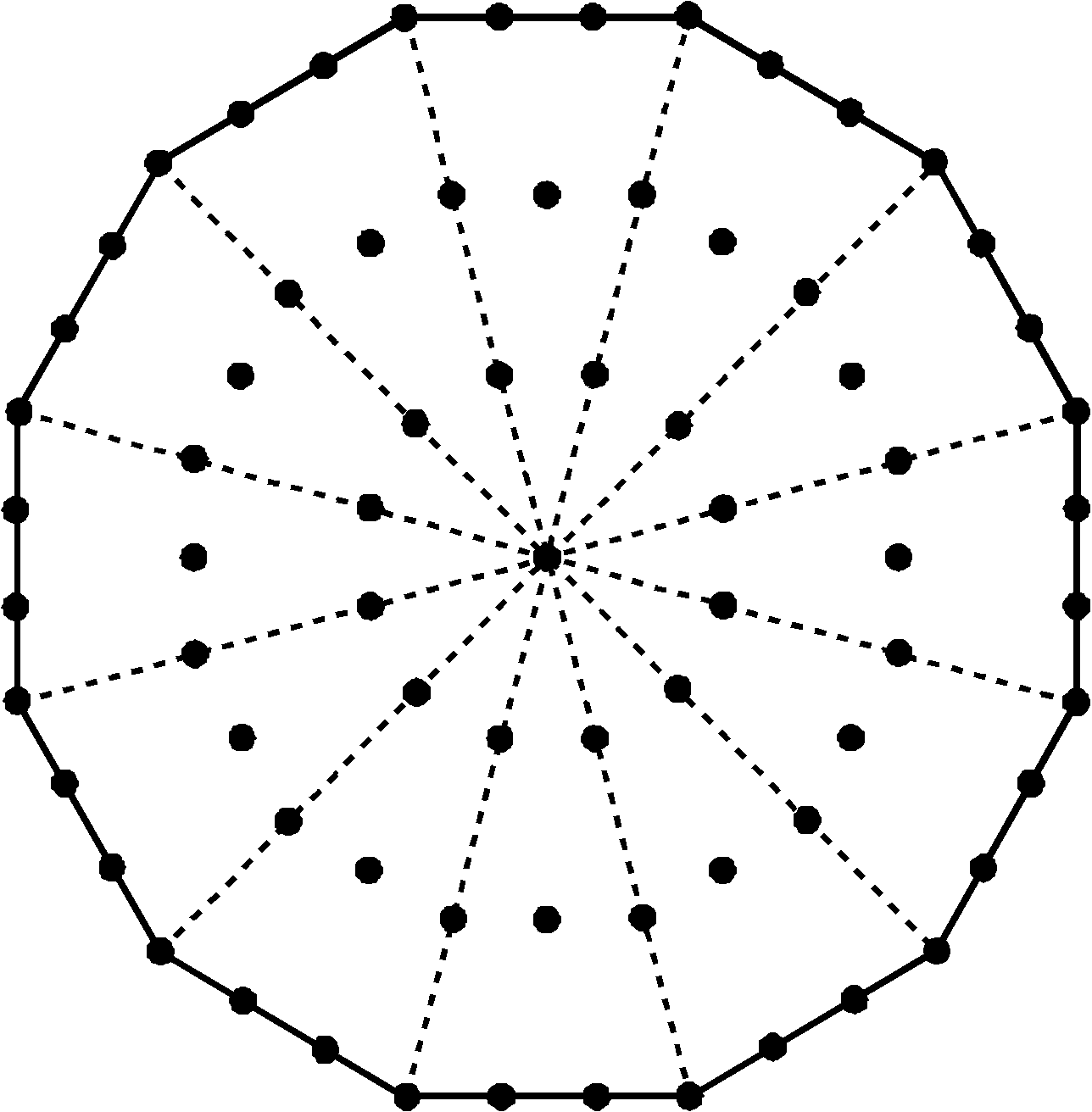
Figure 2. The number 73 of Chokmah is the number of yods lining the three enfolded polygons absent from the inner Tree of Life. It is also the number of yods in a Star of David composed of tetractyses and in a Type A dodecagon.

polygons that is singled out in some way. Given that aleph is the first letter of the Hebrew alphabet, the most appropriate corner is the corner

3

of the heptagon on the axis, this being the simplest of the three polygons. Referring to Table 1, the value 5 of H = 2 + 3 (above axis), the value 5 of the second H = 2 + 3 (below axis) and the value 10 of I = 1 + 4 + 1 + 4, whilst the value 6 of V = 1 + 1 + 1 + 1 + 1 + 1 (Fig. 1). YAHWEH prescribes all 26 corners of the 27 sectors of the three enfolded polygons and EHYEH prescribes the corners of the latter outside the root edge. Remarkably, they embody the number 73 of Chokmah, whose Godname is YAHWEH, because (see Section 2) 73 yods line their boundaries when their 27 sectors are tetractyses (Fig 2). Here is a chance-defying conjunction of two numbers of the same Sephirah in the same context. In fact, three of the five numbers associated with this Sephirah and its manifestation in the four Worlds of Atziluth, Beriah, Yetzirah & Assiyah are present, for, if we start at the upper endpoint of the root edge and move in turn along the boundary of each of the (3+3) enfolded polygons, we will encounter 140 yods, where 140 is the number value of Masloth, the Mundane Chakra of Chokmah! The number 73 is also the number of yods in the 12 tetractyses making up a Star of David, as well as the number of yods in a Type A dodecagon. How remarkable that the number of yods needed to construct the last polygon in the inner Tree of Life should be the minimum required to create the three enfolded polygons that are absent from it!

Returning to the correspondence between dimensions and corners of the 27 sectors of the three enfolded polygons, it seems natural to associate the two endpoints of the root edge with time and the large-scale dimension that extends along the length of a bosonic string. This is because the 24 corners of the sectors that are outside their root edge would correspond to the 24 spatial dimensions transverse to the string. Just as the 24 corners shape the sectors, so, too, oscillations of a string along 24 transverse dimensions create its form. The three centres of the polygons, which are unique because they are corners of sectors but not corners of polygons, could denote the two transverse, large-scale dimensions and the tenth spatial dimension required by M-theory; they, too, have a special status. Just as these centres do not determine the boundaries of the polygons, so these three dimensions play no part in determining the structure of strings. The six corners of the nonagon above or below the axis would denote the six compactified dimensions (there is no alternative set of corners that is as natural because they would have to belong to two polygons), whilst the remaining 15 corners would denote the 15 higher, compactified dimensions beyond the 11-dimensional space-time where supersymmetry holds. It would comprise the five corners of the heptagon, the corner of the nonagon on the axis and the nine corners of the undecagon, i.e., a 5:10 pattern, in keeping with the letter value H = 5 & Y = 10 of YAH, the Godname of Chokmah with number value 15.

2. The (3+3) enfolded polygons embody E₈
Two hexagonal yods lie on each of the n sides of an n-gon with n corners. The number of yods lining its boundary = 2n + n = 3n. A heptagon (n=7), nonagon (n=9) & an undecagon (n=11) have (3×7 + 3×9 + 3×11 = 81) yods on their sides. Enfolded, they have (81−4−4=73) boundary yods. (73−4=69) such yods are outside their root edge, so that both sets of three enfolded polygons have (2×69=138) boundary yods. This number is the sum of the 10 powers of 1, 2, 3 & 4 on the three edges of the Tetrahedral Lambda with 1, the Pythagorean Monad, at its apex (Fig. 3). It is also the number of yods outside the root edge of the two enfolded Type A dodecagons. Amazingly, the last of the regular polygons in the inner Tree of Life needs as many yods to construct it as are needed to create the boundary of the (3+3) enfolded polygons outside their root edge!

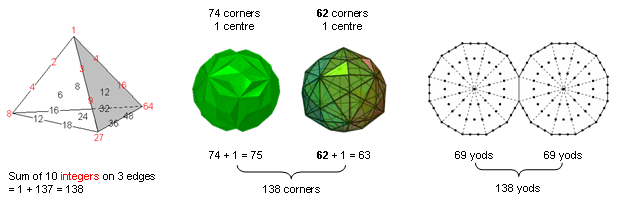
Figure 3. Different holistic systems embody the parameter 138.

.

It was found in Article 58 (p. 6) that the first 10 enfolded, Type A polygons have 74 sectors with 138 sides outside their shared root edge, whilst the two polyhedra making up the Polyhedral Tree of Life (see Article 23) have triangular faces and internal triangles with 138 corners. This embodiment of a parameter of sacred geometries is highly significant, for it is a signature (one of many to

4

be encountered here) of the archetypal status of the three polygons absent from the inner Tree of Life. Including the two endpoints, (138+2=140) yods shape the (3+3) enfolded polygons outside their root edge. As the 27 sectors of the three enfolded polygons have 26 corners, we find that the number values of Chokmah (73), its Godname (26) & its Mundane Chakra (140) measure aspects of this geometry. We shall discover shortly that the number 248 of its Archangel also quantifies it, so that a conjunction of four numbers referring to the same Sephirah will have been established.

Table 3 shows the numbers of yods lining the tetractys sectors of the three enfolded polygons that surround their centres:

Table 3. Number of boundary yods in the three enfolded polygons.

Yods

Heptagon

Nonagon

Undecagon

Total

Corners

5 (10)

7 (14)

9 (18)

21 (42)

Internal hexagonal yods

14 (28)

18 (36)

22 (44)

54 (108)

External hexagonal yods

12 (24)

16 (32)

20 (40)

48 (96)

Total

31 (62)

41 (82)

51 (102)

123 (246)

(numbers refer to yods outside the root edge; numbers in brackets refer to both sets of polygons)

123 boundary yods outside the root edge surround the centres of the polygons. This is the tenth Lucas number, L₁₀. In terms of the Golden Ratio Φ = (1 + √5)/2,

L₁₀ = Φ¹⁰ + Φ^-10.

This demonstrates the influence of the Pythagorean Decad symbolised by the tetractys in expressing holistic parameters like 123 [1]. Including the four yods of the root edge, (123+4=127) yods line the three enfolded polygons. This is the 31st prime number, showing how EL, the Godname of Chesed with number value 31, prescribes the (3+3) enfolded polygons. We found in Article 58 (p. 8) that they contain 310 (=31×10) yods. This is a remarkable illustration of the mathematical design revealed by Godnames in sacred geometries. Outside the root edge are 42 corners and 204 hexagonal yods on sides of tetractyses. Including the two hexagonal yods of the root edge, the two sets of enfolded polygons contain 206 hexagonal yods on the sides of 54 tetractyses and 50 corners, totalling 256 boundary yods, where 256 = 4⁴. This demonstrates the amazing

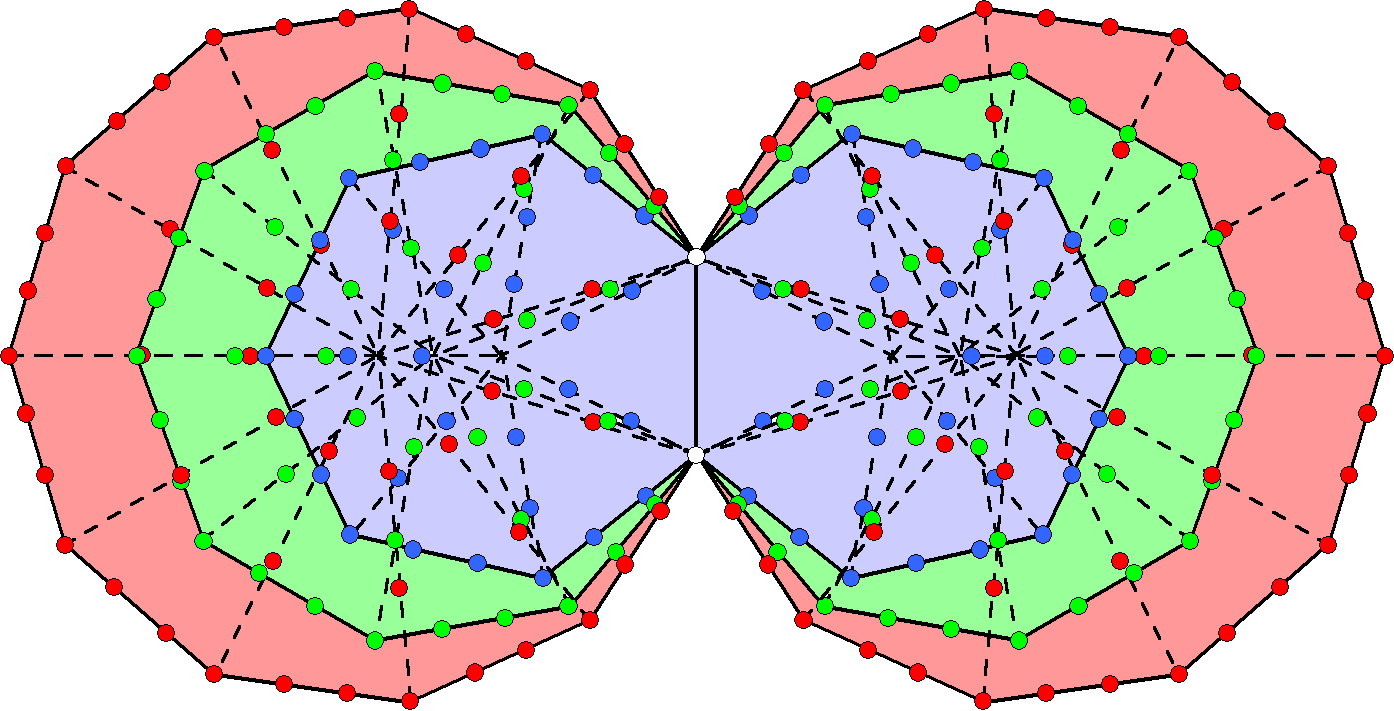
Figure 4. Surrounding the centres of the (3+3) enfolded polygons are 248 yods lining sides of their (27+27) tetractys sectors outside their root edge.

power of the Tetrad to express the beautiful, mathematical properties of sacred geometries. It is a property that the sceptic can dismiss only unconvincingly as yet one more coincidence. As discussed in Article 32 & Article 33, the number 206 is another parameter of holistic systems, manifesting in their human version as the 206 bones in the skeleton.

Including the two endpoints of the root edge, 248 boundary yods surround the centres of the six enfolded polygons (Fig. 4). This is the number value of Raziel, the Archangel of Chokmah. It is the dimension of E₈, the rank-8, exceptional Lie group, that is, the number of its roots and, therefore, the number of the spin-1 gauge fields coupled to their associated charges that transmit the unified force between one of the five types of superstrings, namely, E₈×E₈ heterotic superstrings. Embodied in the three types of polygons absent from the inner Tree of Life is the very master number that determined what kind of matter came to compose the universe. What more convincing evidence can there be of their archetypal status?

E₈ has eight simple roots and 240 roots. What yods denote the former? They cannot include the six centres of the polygons because these are not part of the set of 248 yods. None of the polygons has eight corners — either in total or outside the root edge. The only natural candidates that are left to consider are the two endpoints of the root edge and the corners of the six polygons that lie on the horizontal axis passing through their centres. We say “natural” because it seems reasonable that the simple roots of E₈ should be represented by yods having a special status from a geometrical perspective vis-à-vis the three polygons. In other words, one would not expect, say, some hexagonal yods in one of the polygons to

5

denote all of them because its yods should denote some or all of the roots of only a subgroup, which do not contain all the simple roots of E₈. In other words, yods from all the polygons should be expected to symbolise them because of their global status as simple roots. The mirror symmetry of the distribution of yods would lead one to expect that four yods in each set of three polygons denote four simple roots. The special status of the endpoints of the root edge makes them natural candidates for two of the simple roots and the special status of the three corners lying on the horizontal axis on either side of it makes them candidates, too. In fact, such considerations of symmetry make these eight yods the only plausible candidates to represent the eight simple roots. The six corners on the axis would denote the six simple roots of E₆, the rank-6 exceptional subgroup of E₈, and the two endpoints would denote the two extra simple roots of the latter. Making these choices, Table 4 shows the numbers of yods denoting the 240 roots of E₈:

Table 4. Yods denoting the 240 roots of E₈.

Yods

Heptagon

Nonagon

Undecagon

Total

Corners

4 (8)

6 (12)

8 (16)

18 (36)

Internal hexagonal yods

14 (28)

18 (36)

22 (44)

54 (108)

External hexagonal yods

12 (24)

16 (32)

20 (40)

48 (96)

Total

30 (60)

40 (80)

50 (100)

120 (240)

E₈ has the following numbers of roots in its four exceptional subgroups:

G₂
F₄

E₆

E₇

Number of roots =
12

48

72

126

(the numbers are underlined to indicate that each is a subset of its nearest right-hand neighbour because E₇⊃E₆⊃F₄⊃G₂). It means that there must exist a set of 126 yods that contains a subset of 72 yods, which contains a subset of 48 that, finally, contains a subset of 12 yods. This would be trivially true if we were allowed to choose the yods at random. But, of course, we cannot do this because we expect the yod populations of individual polygons, or combinations thereof, to determine the various dimensions of these Lie groups. This severely limits possible choices of the combinations of the numbers in Table 4. In fact, analysis shows that only one set of combinations is possible:

12 = 12,

48 = 12 + 16 + 20 = 12 + 16 + 20

(the number 16 refers to the corners of the two undecagons);

72 = 48 + 8 + 16 = 8 + 12 + 16 + 16 + 20

and

126 = 72 + 14 + 18 + 22 = 8 + 12 + 14 + 16 + 16 + 18 + 20 + 22.

The 168 roots of E₈ that are not roots of E₆ have the yod counterparts:

168 = 16 + 28 + 24 + 36 + 44 + 20 = (16+24+44) + (28+36+20) = 84 + 84.

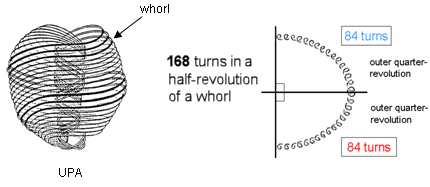
Figure 5. Each helical whorl of the UPA/subquark superstring conforms to the 84:84 division displayed by holistic systems because each half-revolution comprises 168 turns and each quarter-revolution comprises 84 turns.

6

The chosen distribution satisfies the requirement, established by many analyses of sacred geometries in previous articles, that 168 = 84 + 84, reflecting the fact that holistic systems display two halves. The subatomic manifestation of this is the UPA/subquark superstring (Fig. 5). Each of its 10 whorls is a helix with 1680 (=168×10) circular turns. 840 (=84×10) turns in its outer half wind around its spin-axis and 840 turns in its inner half wind around it in a narrower spiral.

3. The (3+3) enfolded polygons embody E₈×E₈

This section will reveal that the three enfolded polygons have a geometrical composition in terms of elementary points, lines & triangles that is analogous to the root composition of E₈, the rank-8 Lie group. The presence of their mirror-image counterparts has the important implication that the archetypal set of (3+3) enfolded polygons absent from the inner Tree of Life has a geometry that is analogous to E₈×E₈, which several earlier articles have shown is embodied in the yod composition of the (7+7) enfolded polygons. Far too many correlations with the exceptional subgroup structure of E₈ will be established to make it plausible that it is just coincidence that a simple, geometrical object suspected of being sacred geometry has properties analogous to the root composition of one of the two possible symmetry groups that describe superstring forces.

A Type B n-gon is an n-sided polygon whose n sectors are Type A triangles, i.e., each is divided into three sectors. Table 5 shows its geometrical composition:

Table 5. Geometrical composition of a Type B n-gon.

Corners

Sides

Triangles

Total

external

internal

external

internal

n

n + 1

n

4n

3n

10n + 1

The heptagon (n=7), nonagon (n=9) & undecagon (n=11) have 27 external corners and (27+3=30) internal corners, i.e., 57 corners in total. Their (3×27=81) triangles have 27 external sides and (4×27=108) internal sides, totalling 135 sides. Hence, they have (57+135=192) corners & sides, (57+81=138) corners & triangles, (135+81=216) sides & triangles and 273 corners, sides & triangles. Both sets of polygons have 384 corners & sides, 189 corners & sides surrounding the three centres of each set. The appearance of the holistic parameters 192 & 384, which have been discussed numerous times in previous articles, as well as the division:

192 = 3 + 189

between their three centres and 189 corners & sides are the first signs that this article presents of the archetypal status of these three polygons. 21 polygonal corners are outside their left-hand sides, so that

189 = 21 + 168

and

192 = (3+21=24) + 168.

This 24:168 division is another sign of the holistic character of the three absent polygons. For example, its counterpart in the 192 lines & broken lines that make up the 64 trigrams in each diagonal half of the 8×8 square array of hexagrams in the I Ching system of divination is the 24 lines & broken lines in the eight diagonal trigrams and the 168 lines & broken lines in the 56 off-diagonal trigrams.

When enfolded, only the left-hand sides of the three separate polygons merge into the shared root edge (no other geometrical elements coincide), so that two sides and their four endpoints disappear. Table 6 shows the geometrical composition of the three enfolded polygons and the (3+3) enfolded polygons:

Table 6. Geometrical composition of the three enfolded Type B absent polygons.

Polygon

Corners

Sides

Triangles

Total

external

internal

external

internal

Heptagon
2 + 5 = 7

7 + 1 = 8

1 + 6 = 7

28

21

3 + 67 + 1

Nonagon

7

9 + 1 = 10

8

36

27

87 + 1

Undecagon
9

11 + 1 = 12

10

44

33

107 + 1

Total
2 + 21 = 23

27 + 3 = 30

1 + 24

108

81

3 + 261 + 3 = 264 + 3

(numbers in cells for the nonagon & undecagon denote the geometrical elements outside their left-hand sides)

264 geometrical elements ((23+27=50) corners, (1+24+108=133) sides & 81 triangles) surround the

7

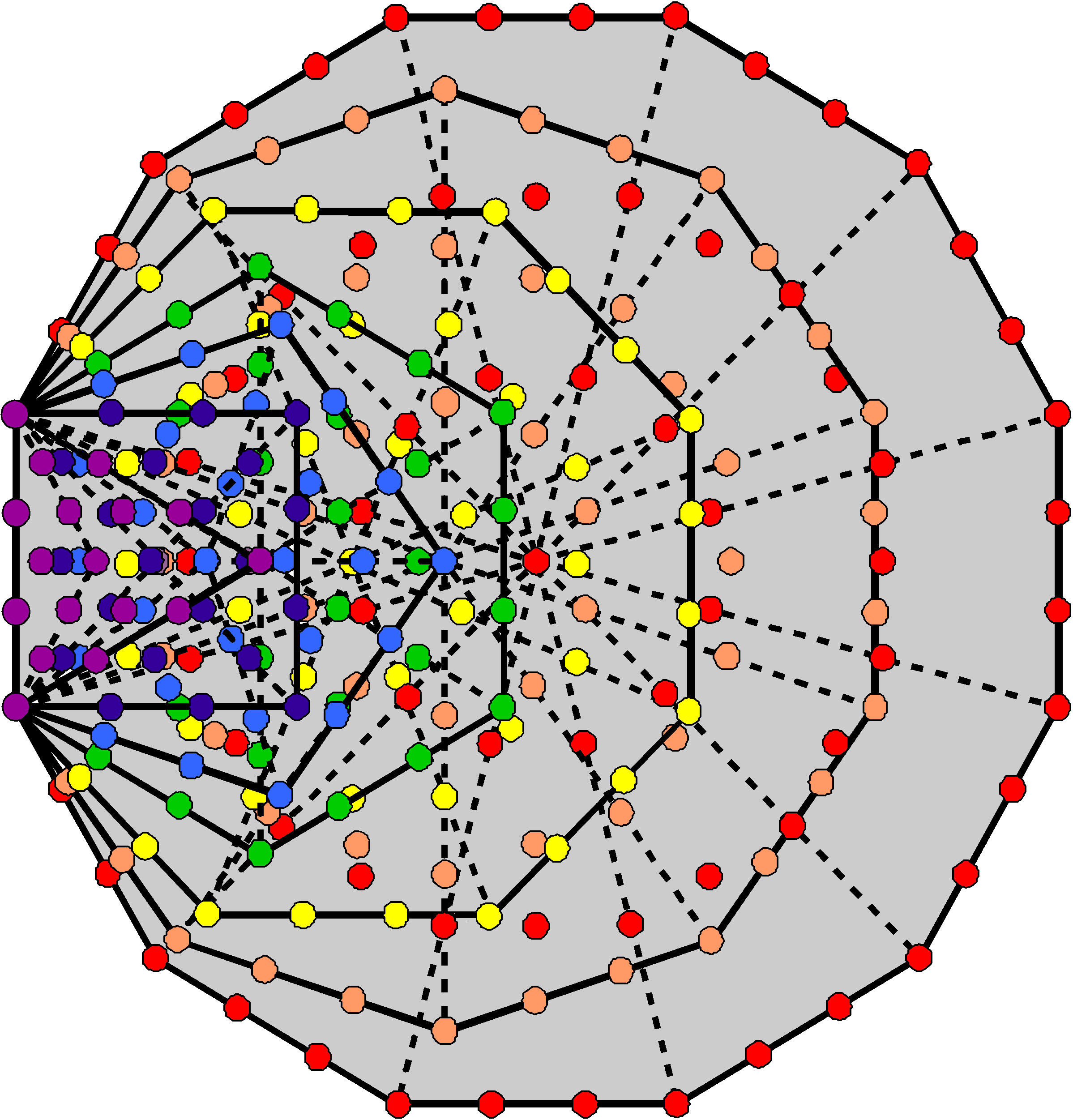Figure 6. Transformed into tetractyses, the 47 sectors
of the 7 enfolded polygons contain 264 yods.

centres of the three enfolded polygons. This is a basic parameter of holistic systems because the seven enfolded Type A polygons constructed from tetractyses contain 264 yods (Fig. 6). 131 corners & triangles surround the three centres, where 131 is the number value of Samael, the Archangel of Geburah. The (3+3) enfolded polygons have (2×108=216) internal sides, where 216 is the number of Geburah, and 49 external sides, where 49 is the number value of EL ChAI, the Godname of Yesod. 264 sides are outside their shared side. (264–3=261) geometrical elements outside the root edge in the three polygons surround their centres. They comprise the 21 corners of the three enfolded polygons and 240 geometrical elements (27 corners of triangles, 132 sides & 81 triangles). The centres of the (3+3) enfolded, Type B polygons are surrounded by (240+240=480) geometrical elements outside the root edge, apart from their (21+21=42) corners. In other words, (240+240) geometrical elements are outside the root edge other than the (24+24=48) corners of their (27+27) sectors. They correspond to the (240+240) roots of E₈×E₈. The eight simple roots of E₈ correspond to the five corners of the heptagon outside the shared side and the centres of the three polygons. Although the nonagon has seven corners outside the shared side, only one centre would have to be included to represent the eight simple roots. This leaves out the two other centres, so that this choice does not seem natural, given the comparable status of these roots and centres of polygons. It does seem natural to associate the five external corners of the heptagon and its centre with the six simple roots of E₆.

It is not unexpected that the number 240 should manifest here because many previous articles have established it as a defining parameter of sacred geometries. What is surprising is that it should appear in the three polygons not present in the sacred geometry of the inner Tree of Life! Either it confirms the conclusion reached in Article 58 that the first 10 polygons have an archetypal status or its appearance is a coincidence to be dismissed along with all the other alleged coincidences established in that article. The following considerations expose the implausibility of this possibility.

If an analogy truly exists between the roots of E₈ and the geometrical elements making up the three enfolded polygons, we should expect to find the numbers of roots in its exceptional subgroups in successively smaller subsets of the set of 240 geometrical elements. In other words, there should exist a set of 48 geometrical elements that contains a subset of 12 elements and which belong to a larger set of 72 elements, which should be part of a larger group of 126 elements within the set of 240 elements. If this is the case, can the sceptic dismiss this, too, as yet more coincidences? What is the likelihood of that!? Obviously, it would not be a reasonable view to defend. As shown next, this pattern does exist. Moreover, we shall show that the set of 240 geometrical elements consists of 10 sets of 24 elements, confirming the conclusion of Article 53 that five sacred geometries embody 240 structural elements as 10 sets of 24, reflecting the 10-fold nature of the Divine Unity that they represent.

Figure 7. The 240 roots of E₈ correspond to the 240 geometrical elements of the three enfolded Type B polygons other than corners that are outside the root edge and surround their centres. Three sectors share the root edge.

Table 6 indicates that the three enfolded polygons have 24 sides outside their shared side. Twelve are above the horizontal axis passing through their centres and 12 are below it. One sector of each Type B polygon has the root edge as their shared side. Figure 7 depicts these sectors, the sides of the three basic triangles in each Type A triangular sector being shown as dashed lines. This leaves 24 sectors that share none of the 240 geometrical elements outside the root edge, which is the only shared part of the polygons. Other than polygonal corners, which we can ignore because they do not belong to the set of

8

240 geometrical elements, and polygonal sides, which we just considered, there are eight geometrical elements per sector:

side of sector + 3 sets of sides of triangles + 3 triangles + shared corner of 3 triangles

Hence, the three sectors sharing the root edge have 24 geometrical elements intrinsic to them. This leaves 24 sides of 24 sectors, each with (3+3+1=7) internal elements, i.e., (24×7=168) such elements. Surrounding the centres of the three enfolded polygons are:

12 polygonal sides above the axis and their 12 counterparts below it;

24 sides of sectors not sharing the root edge;

24 geometrical elements inside the three sectors sharing the root edge;

24 sets of seven internal elements, or seven sets of 24 elements, all elements in a set being the same type.

The following correspondences exist between the exceptional subgroups of E₈ and the composition of the sectors of the three enfolded, Type B polygons:

12 polygonal sides in either half → 12 roots of G₂;

24 polygonal sides + 24 sides of sectors not sharing the root edge → 48 roots of F₄;

24 polygonal sides + 24 sides of sectors + 24 geometrical elements inside the three sectors sharing the root edge → 72 roots of E₆.

Also surrounding the three centres are 54 internal elements of the 24 non-shared sectors of which A elements belong to each of the six such sectors of the heptagon, B elements to each of the eight such sectors of the nonagon & C elements to each of the 10 such sectors of the undecagon, where

54 = 6A + 8B + 10C (A, B, C = 0-7)

(It is readily verified that several such solutions to this equation exist, e.g., A = 0 & B = C = 3; for the present purpose, they need not be listed here). This means that the three polygons allow 126 elements to be selected from the 240 present in them. Given the many possible sets of elements within the master set, this is not really surprising. What is non-trivial, however, is how natural the numbers for the roots in the smaller, exceptional subgroups of E₈ appear in the geometry. There is nothing contrived or artificial about

Figure 8. 480 geometrical elements surround the centres of the seven separate Type B polygons.

their counterpart sets of yods. Still more remarkable is how the 240 geometrical elements naturally divide into 10 sets of 24 elements. The 72 elements comprise three sets of 24, whilst the fact that each Type A triangular sector comprises seven internal elements means that the remaining 168 elements consist of seven sets of 24 elements. In the former case, all elements are present in each set of 24; in the latter case, they are all of the same type. The 10-fold factor arises because the polygons are composed of 10 types of geometrical elements; the set size of 24 arises because the three types of polygons have 27 sectors, of which three share the root edge, leaving 24 unshared sectors, each with seven internal geometrical elements.

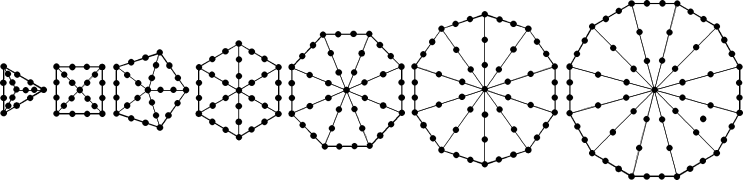
Figure 9. 240 yods lining their sectors surround the centres of the seven separate Type A polygons of the inner Tree of Life.

9

Noting that an n-gon has 10n geometrical elements surrounding its centre, the three enfolded, Type B polygons are equivalent in geometrical composition to a Type B 24-gon, whose centre is surrounded by 240 geometrical elements as 24 sets of 10 elements, that is, as 10 sets of 24 elements. A Type B 48-gon has 48 sectors with 480 geometrical elements surrounding its centre. The counterpart of this in the inner Tree of Life is its seven separate, Type B polygons with 480 geometrical elements surrounding their centres (Fig. 8), the triangle, square, pentagon & dodecagon having 240 such elements, as does the hexagon, octagon & decagon. Embodied in the (3+3) enfolded Type B polygons are the very geometrical parameters 240 & 480 that characterise the geometrical composition of the inner Tree of Life! This is no accident, because the Supernal Triad is the archetypal source of the seven Sephiroth of Construction and the three polygons that formally correspond to them in the sense that the first 10 polygons bear a correspondence to the 10 Sephiroth contain the same information as that which is embodied in the seven polygons corresponding to the seven Sephiroth of Construction. That is why exactly the same holistic pattern of numbers exists in both sets of polygons, e.g., 240 yods that line their sectors surround the centres of the seven separate Type A polygons (Fig. 9), just as they do in the (3+3) enfolded polygons apart from those corners on the horizontal axis that denote some of the simple roots of E₈.
The 3:7 distinction in the types of geometrical elements arises from the distinction between Type A polygons, whose sectors are defined by three geometrical elements (one corner & two sides per sector), and Type B polygons, whose sectors are further divided into three sectors with seven types of geometrical elements (one corner, three sides & three triangles).

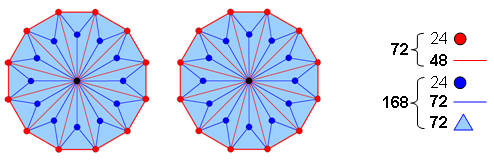
Figure 10. The two separate Type B dodecagons in the inner Tree of Life have 240 geometrical elements surrounding their centres. 72 red elements make up the sides of the two Type A dodecagons and 168 blue elements make up their 24 sectors.

The 3:7 division in the geometry of a Type B polygon reflects the difference between the three archetypal Sephiroth of the Supernal Triad and the seven Sephiroth of Construction. It manifests in the last polygon of the inner Tree of Life as the 72:168 division in the 240 geometrical elements that surround the centres of the two separate Type B dodecagons (Fig. 10).

120 yods line the boundaries of the seven enfolded polygons. The shape of the two separate sets of seven enfolded polygons is defined by the 240 yods lining their sides. Remarkably, they naturally form 10 sets of 24 yods (Fig. 11). As pointed out earlier, the same 10-fold pattern manifest in other sacred geometries (see Article 53), such as the

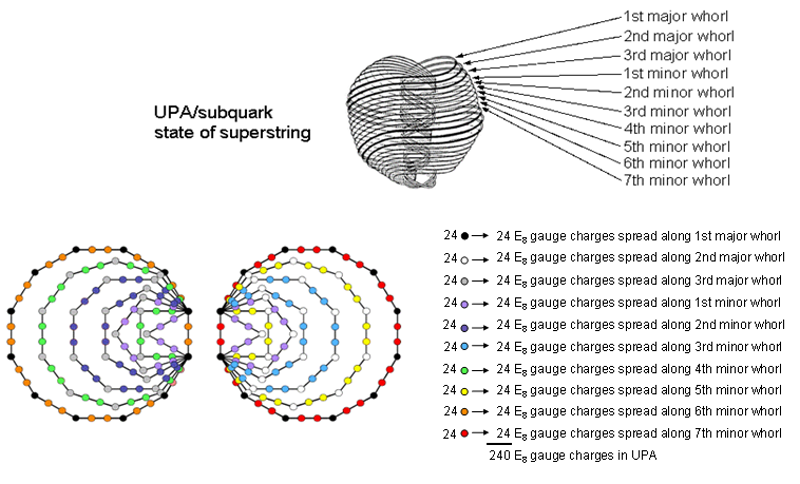
Figure 11. The 10 groups of 24 yods on the sides of the two sets of seven enfolded polygons of the inner Tree of Life symbolize
the 10 whorls of the UPA/subquark superstring, along each of which 24 E₈ gauge charges are spread.

10

five Platonic solids and the Sri Yantra. It represents the 10-fold structure of the E₈×E₈ heterotic superstring, described by Annie Besant & C.W. Leadbeater over a century ago when they remote-viewed subatomic particles, such as like protons and quarks. 24 E₈ gauge charges are spread along each whorl, so that the UPA carries 240 such charges corresponding to the 240 roots of the gauge symmetry E₈ that describes its unified force. They are the physical counterpart of the 10 sets of 24 yods or 24 geometrical elements that define the shapes of both the (3+3) enfolded polygons and the seven types of polygons of the inner Tree of Life. The 72:168 division displayed in them manifests in the subquark state of the E₈×E₈ heterotic superstring as the distinction between the three major whorls, which bear a correspondence to the Supernal Triad of Kether, Chokmah & Binah and which carry (3×24=72) E₈ gauge charges, and the seven minor whorls, which correspond to the seven Sephiroth of Construction and carry (7×24=168) E₈ gauge charges. It expresses the breakdown of E₈ symmetry with 240 roots into that of E₆ with 72 roots. This is a truly remarkable meeting of sacred geometry, theoretical physics and the paranormal. Let those who might be sceptical that the inner Tree of Life and the three polygons that are absent from it are examples of sacred geometry — in spite of their remarkable properties discussed in this article and at the author's website — ponder on the fact that this claim does not rest on the assumption that they are such examples. This is because Article 53 established that other geometries, such as the outer Tree of Life and the Sri Yantra, which are universally recognised as sacred geometries, exhibit exactly the same patterns and the same number 240. Let those who do not think that it is possible to remote-view subatomic particles ask themselves if they can really believe that the number 1680 recorded by Besant & Leadbeater appears just by accident in these geometries, along with the gematria number values 248, 496 and 168, which are of significance to superstring theory. For that is the implausible position that their disbelief forces them to hold. Let those who cannot believe in the possibility of sacred geometries representing the divine design try to explain away in terms of chance the remarkable coherence and mathematical beauty displayed in them, as revealed through the gematria numbers of the 10 Sephiroth in the four Kabbalistic Worlds. Can they, for example, really believe that the possession of 4⁴ yods on the sides of the sectors of the (3+3) enfolded polygons that are absent from the inner Tree of Life is as random and accidental as a splash of paint on a Jackson Pollock drip painting?

References
1. The number 123 is a defining parameter of holistic systems. For example, when their faces are divided into their sectors and the internal triangles formed by joining their vertices to their centres are divided into their sectors, the five Platonic solids have 1230 corners, sides & triangles surrounding their centres. Each half of a Platonic solid on average is composed of 123 geometrical elements (see Table 4 in The holistic pattern). On average, surrounding the centres of these solids are 246 such elements, where 246 is the number value of Gabriel, the Archangel of Yesod. This is the number of yods outside the root edge that line the tetractys sectors of the (3+3) enfolded polygons absent from the inner Tree of Life. The same number re-appears in different holistic systems because they embody the same, archetypal pattern. What is so highly significant is not that they may have different meanings in each context but that they should exist at all in these systems as quantifiers of their global properties. This re-occurrence in recognised sacred geometries, as well as in what the author claims are examples of such, cannot, sensibly, be attributed to chance. Let us be honest: that assertion is merely a desperate explanation resorted to by sceptics who are unwilling to deal with the profound (and, to them, unsettling) philosophical implications of the existence of the same numerical patterns in various sacred geometries.

11