.png)

| << Previous 1... 2 3 [4] 5 6 ...24 Next >> |
#4The superstring parameters 70 and 42 as parameters of sacred geometries
|
In terms of the classical theory of the five Elements, the UPA described by Besant & Leadbeater is the basic particle of physical matter that is compounded from the four Elements of Earth, Water, Air & Fire, whilst the basic particle of shadow matter corresponds to Aether, the fifth Element. In Theosophical language, the former particle is the basic constituent of matter belonging to the lowest three subplanes of the physical plane and the latter is its counterpart in the four highest subplanes of the physical plane. Where Besant & Leadbeater were wrong was in thinking that all physical matter — whether belonging to what they called the three "dense physical" subplanes or to the four etheric subplanes — had to be composed ultimately of the same, fundamental building block. The distinction between the two kinds of matter is not merely one of complexity of aggregation, as they thought (this is where the notion of the all-inclusive Aether in contemporary Victorian science misled them). Rather, it amounts to a real difference of category. Ascribing their essential difference merely to their relative densities, as Besant & Leadbeater did, is too naive and simplistic if one wants to explain shape-shifting, materializing, etheral entities like ghosts and fairies that many human cultures have reported over the centuries. For example, how can etheric matter be normally invisible if it is composed of a particle (the UPA, according to Besant & Leadbeater) that, because it makes up atomic nuclei, must be electrically charged in order to endow them with electric charge as well, so that the particle must be capable of scattering and emitting light, just as electrons do? Besant's and Leadbeater's understanding of the nature of etheric matter was little more than the logical extension of their understanding of the three lowest subplanes of the physical plane. For these two Theosophists, matter exists on each of these subplanes according to whether it is solid, liquid or gaseous, i.e., it is simply an issue of its density as bulk substance. For two people who argued throughout their lives against the scientific materialism of their age, this seems a crass, materialistic way of distinguishing between levels of physical awareness! For they were talking about planes and subplanes of consciousness — both physical and superphysical. What has that got to do with whether I see an object as solid, liquid or gaseous?! My level of awareness does not alter whilst my eyes watch an object melt, then vaporize as I heat it further. Their classification in terms of states (rather than kinds) of matter has certainly nothing to do with the ancient belief in the four physical Elements, which makes metaphorical reference to four, not three, states of matter, although this was never the meaning (exoteric or esoteric) of this ancient teaching, which regarded different substances as a mixture (in various proportions) of the particles that make up earth, water, air and fire. The difference of physical state given by Besant & Leadbeater to matter belonging to the three "dense physical" subplanes is consistent with their mistaken belief that the density or the degree of complexity of aggregates of UPAs solely determines to which subplane their bound states belong. But this consistency is about the only merit to be found in their explanation of the seven physical subplanes. This is not to blame or to fault but to recognise an honest error in their understanding that led to a weakness in their general account of what the physical plane is and how its subplanes should be distinguished. It is simply that physics has advanced considerably from their days, which were several decades before the era of atomic and nuclear physics. Having evaluated their discoveries known as "Occult Chemistry," we need to realise that the interpretations they made of their remote-viewings was influenced by their own education and understanding and by the scientific times that they lived in — just as it must be for anyone today who claims similar abilities. Correcting one of these interpretations does not undermine their achievements. On the contrary, it creates a new perspective, from which their clairvoyant work can be better evaluated and appreciated. |
It was argued earlier that each gauge charge associated with one of the 240 non-zero roots of E8 is spread along a whorl of the UPA (E8′-singlet state of the E8×E8′ heterotic superstring) as 70 circular turns, or circularly polarised waves, and that each E8′ gauge charge is spread along a whorl of the basic shadow matter particle described by Cowen as 42 circularly polarised waves. It was shown also that the number of circularly polarised waves per revolution of a whorl is the same for both types of superstring, namely, 336, and that this is because the number is a structural parameter of several sacred geometries. This is true for the number 70 as well, as the following examples demonstrate:
.png) |
 |
 |
 |
 |
 |
| (a) The outer Tree of Life contains 70 yods. | (b) There are 70 sides of triangles in the 16 Type A triangles in the outer Tree of Life. | (c) The (7+7) enfolded polygons of the inner Tree of Life have 70 corners. | (d) The 2nd-order tetractys contains 70 hexagonal yods. | (e) Including the bindu, there are 70 points in the 2-d Sri Yantra. | (f) Each set of halves of the five Platonic solids comprises 70 vertices & edges. |
a) When its 16 triangles are turned into tetractyses, the outer Tree of Life has 70 yods;
b) When its 16 triangles are Type A, the outer Tree of Life has 48 triangles with 70 sides;
c) The inner Tree of Life consists of (7+7) enfolded polygons with 70 corners;
d) The 2nd-order tetractys is the next higher differentiation of the 1st-order tetractys. It has 85 yods, where
85 = 40 + 41 + 42 + 43,
of which 15 (= 42 − 40) are corners, leaving 70 hexagonal yods, where 70 = 85 − 15 = (40+40) + (41+43) = 2 + 68 (the significance of this sum will be discussed shortly);
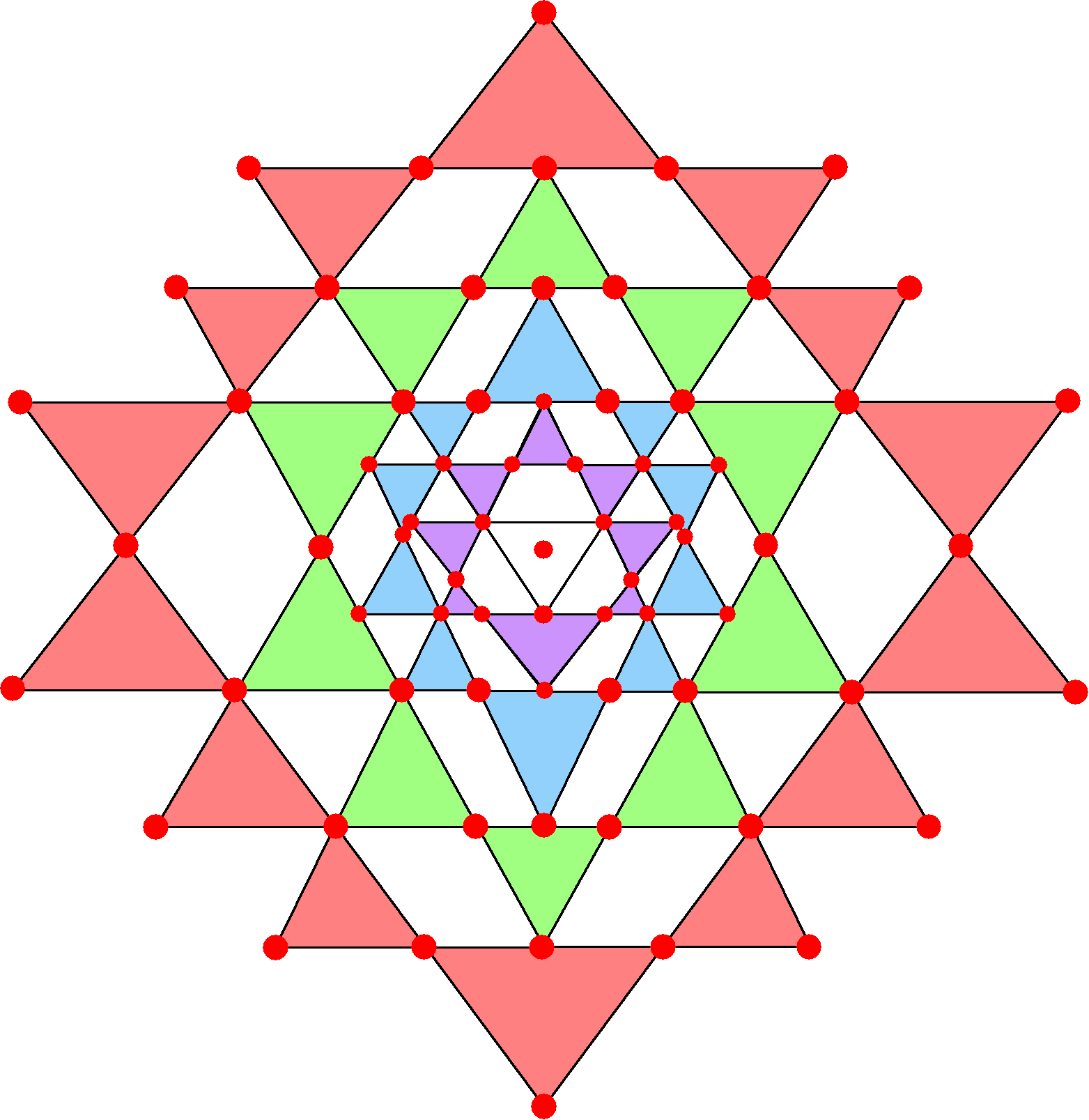
e) The 43 triangles in the 2-d Sri Yantra comprise:
bindu: 1 point;
lower corner of central triangle: 1 corner;
8 violet triangles: 12 corners;
10 blue triangles: 16 corners;
10 green triangles: 12 corners;
14 red triangles: 28 corners.Total = 70 corners/points.
f) The five Platonic solids have 50 vertices and 90 edges, i.e., 140 vertices & edges. Each mathematical half of a Platonic solid is the set of one-half of the total number of each type of geometrical element that composes its faces and interior. A set of five halves has 70 vertices & edges. They comprise:
|
Vertices |
Edges |
|
| Tetrahedron |
2 |
3 |
| Octahedron |
3 |
6 |
| Cube |
4 |
6 |
| Icosahedron |
6 |
15 |
| Dodecahedron |
10 |
15 |
| Total |
25 |
45 |
The division: 70 = 2 + 68, which case d indicates is generated by expressing this number in terms of powers of 4 (the Pythagorean Tetrad), appears in:
The division manifests because these sacred geometries are equivalent representations of the archetypal pattern underlying holistic systems. They possess multiple isomorphic patterns. For example, the Tree of Life with 70 yods has a trunk with 25 hexagonal yods, leaving 45 yods, and this 25:45 split appears also in its geometry as the 25 sides of the 15 triangles in its trunk and the 45 sides in its branches. Each set of five halves of the Platonic solids has 25 vertices and 45 edges (see the table shown above), whilst the 2-d Sri Yantra has 25 corners in the central triangle, the violet triangles and the green triangles and 45 corners comprising the bindu, the 16 corners of the blue triangles and the 28 corners of the red triangles. The first six enfolded polygons that are part of each half of the inner Tree of Life have 26 corners, so that 25 corners are associated with either set of these polygons, leaving 45 corners of the other eight polygons. Realising that these sacred geometries are isomorphic should remove the sense of surprise (but not the wonder) felt when one encounters their embodiment of the same number and the same pattern of its division. The sceptic may argue that any subset of objects of the required number can always be cherry-picked from a given set of objects. What he ignores, of course, is that this can be done only in a random manner by picking different classes of objects to form the required number. It cannot always be done if the required subset has to be homogenous because it is a category of objects that share a trait — there may not be enough that are alike that are available for picking; alternatively, there may be too many of the right kind. A pattern will be significant (and incapable of being cherry-picked) if the different categories displaying this pattern are exclusive in the sense that all the objects possessing a given category are assigned to the same subset. The numbers forming an archetypal pattern have to quantify complete, homogeneous subsets of structural elements of the same class — a restriction that is highly unlikely to be satisfied through any process of cherry-picking, which can create only heterogeneous subsets composed of different classes of objects.
Having established that sacred geometries embody in a natural way the number 70 that is a structural parameter of the subquark state of the E8×E8′ heterotic superstring, the question arises: do they embody as well the other structural parameter 42? Just because it parameterizes the basic unit of a form of matter that happens to be invisible to human beings (for all we know, it may be visible to extra-terrestrial life-forms) is no reason to ignore it as though it were less important. It most certainly is not, for superstring theory asserts that shadow matter is associated with one of the two similar symmetry groups that describe the forces of nature and their sources; it is no less fundamental than ordinary matter. In fact, astronomicaly speaking, it is more important because it makes up most of the matter in the universe. The number 70 is the number of circularly polarised waves in a whorl of an E8′-singlet state of an E8×E8′ heterotic superstring that express one gauge charge of E8; the number 42 is the number of circularly polarised waves in a whorl of an E8-singlet state expressing one gauge of of E8′. The symmetry-breakdown of E8′ need not be the same as that of E8 and the waves express their gauge charges according to numbers that do not depend upon whatever subgroups these charges may define. Can the number 42 appear within a subset of the 70 structural elements even though these elements correspond to physically different types of particle? Yes, provided that the sacred geometry represents not both particles simultaneously but either particle. The meaning of global parameters depends on the holistic system in question that the sacred geometry represents. The numbers themselves do not change, only their meaning. This permits the subset of 42 elements to have the same type of meaning as all 70 elements — the sacred geometry in question can represent a different particle in which categories are differently quantified, e.g., because different combinations of the structural elements are considered. Sacred geometries are not a case of "one size fits all." Only the overall design and pattern of numbers quantifying different categories must be the same. The morphology of sacred geometries is immaterial. Only the hidden pattern of numbers that they represent counts. For it is universal.
What this means for the subquark and the basic particle of shadow matter is that we can look for the number 42 referring to the latter in the various cases that have already been considered. Let us start with case d, as it is very straightforward.
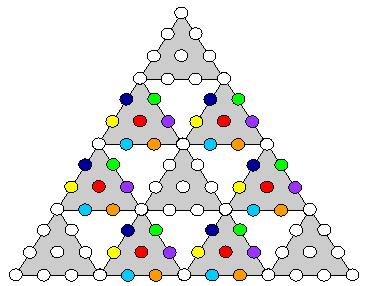 |
The 3:7 distinction between corners and hexagonal yods in the 10 yods of the 1st-order tetractys becomes the 15:70 distinction in the 85 yods of the 2nd-order tetractys. Instead of being symbolised by six hexagonal yods at the corners of a hexagon, the six Sephiroth of Construction above Malkuth become associated with (6×7=42) coloured yods, leaving 42 white yods surrounding the centre that are associated with either the Supernal Triad or Malkuth. This 42:42 division of the holistic parameter 84 manifests in CTOL as the 42 subplanes of the six cosmic superphysical planes and the 42 subplanes of the six planes above the physical plane, which is symbolised by the hexagonal yod at the centre of the central 1st-order tetractys. In each case, the number 42 measures all the superphysical levels. The 42 pairs of corresponding subplanes have their counterpart in the particle of shadow matter as the 42 pairs of perpendicular plane waves expressing each gauge charge of E8.′ In general, it expresses the 42 differentiations of the six Sephiroth of Construction above Malkuth. |
Now consider case e:
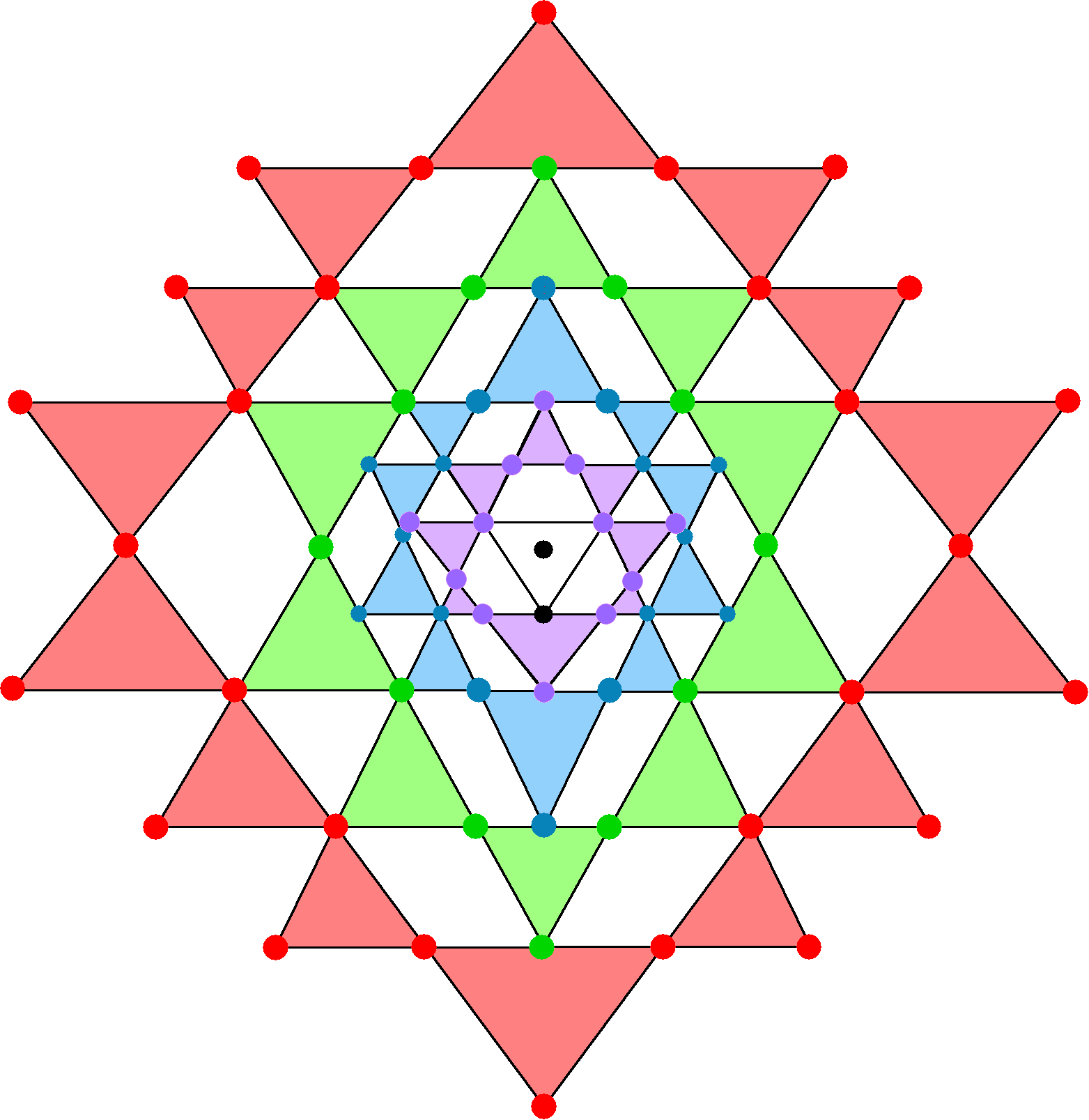 |
The 14 outermost, red triangles of the 2-d Sri Yantra have 28 red corners, so that there (70−28=42) points that comprise the bindu (black dot at the centre of the central triangle), the lowest (black) corner of the central triangle and the 40 corners (12 violet, 16 blue, 12 green) of the 28 violet, blue & green triangles:
The number 42 is also the number of triangles that surround the central triangle. It is therefore both part of the number 70 (total number of points in the 2-d Sri Yantra) and separate from it as a distinct parameter in its own right. The 42:28 division corresponds in the 2nd-order tetractys to the 42 coloured hexagonal yods and the 28 white hexagonal yods. |
Next, consider case c:
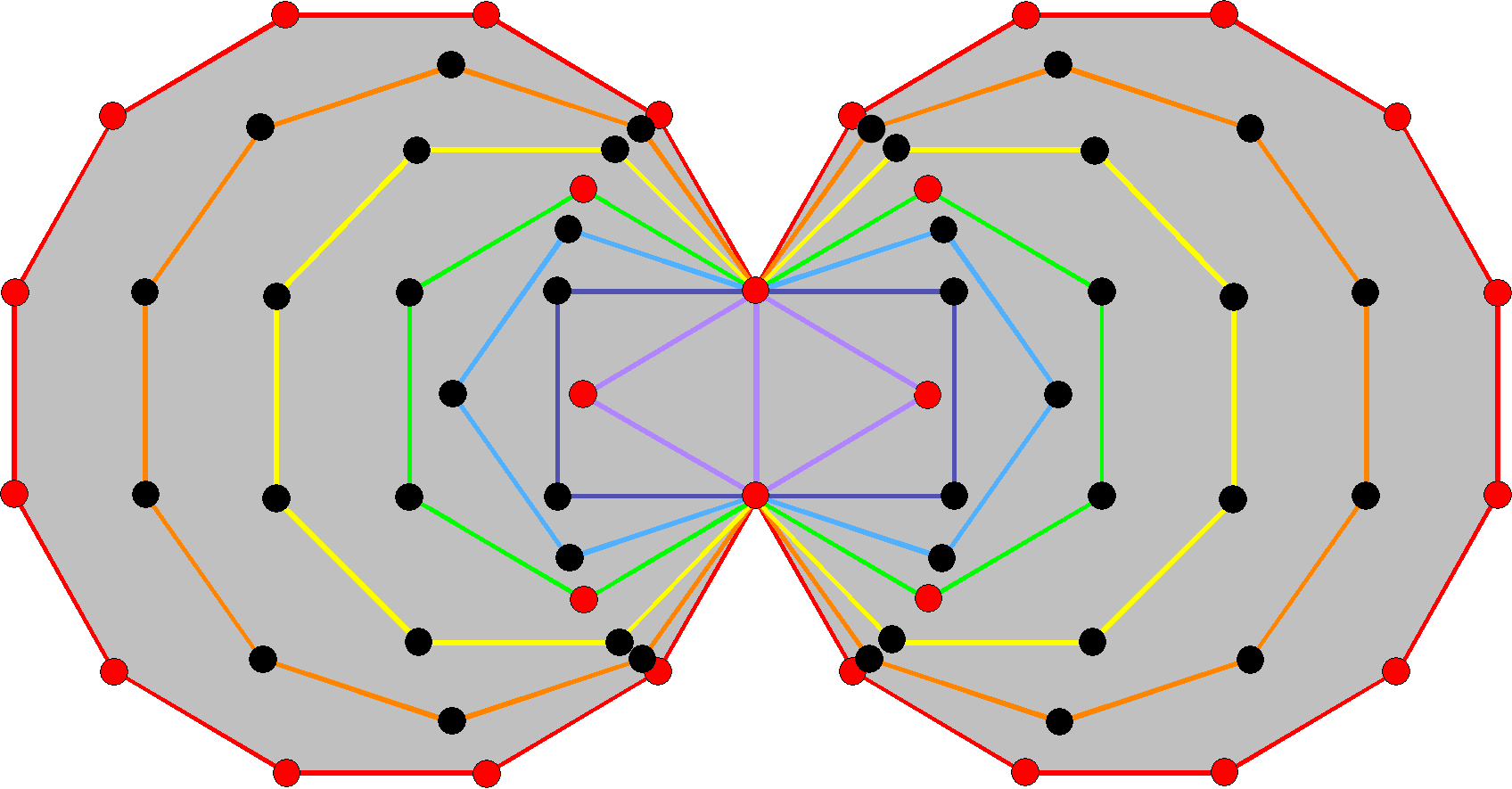 |
The (7+7) enfolded polygons making up the inner Tree of Life have 70 corners. The top and bottom red corners of each hexagon and its red centre coincide with corners of triangles that belong to the outer Tree of Life. The first (6+6) enfolded polygons have 50 corners, of which 42 black corners are both outside the root edge and intrinsic to the inner Tree of Life. The 70 corners comprise these 42 corners and 28 remaining red corners that are either shared with the outer Tree of Life or belong to the pair of dodecagons, which embody properties that express the Malkuth, or formative, aspect of the Tree of Life. Hence, there are 42 black corners intrinsic to the inner Tree of Life that express what pertains to the six Sephiroth above Malkuth. The 21 such corners in each set of enfolded polygons correspond to the 21 points that can be associated with each half of the 2-d Sri Yantra (see case e): |
Now consider case f. If we divide each Platonic solid into its two halves, each set of five halves comprises 25 vertices and 45 edges. The tetrahedron has six edges (three in each half). The octahedron, cube, icosahedron & dodecahedron have 42 edges in each set of halves (21 edges in the octahedron & icosahedron and 21 edges in the cube & dodecahedron).
Then consider case a:
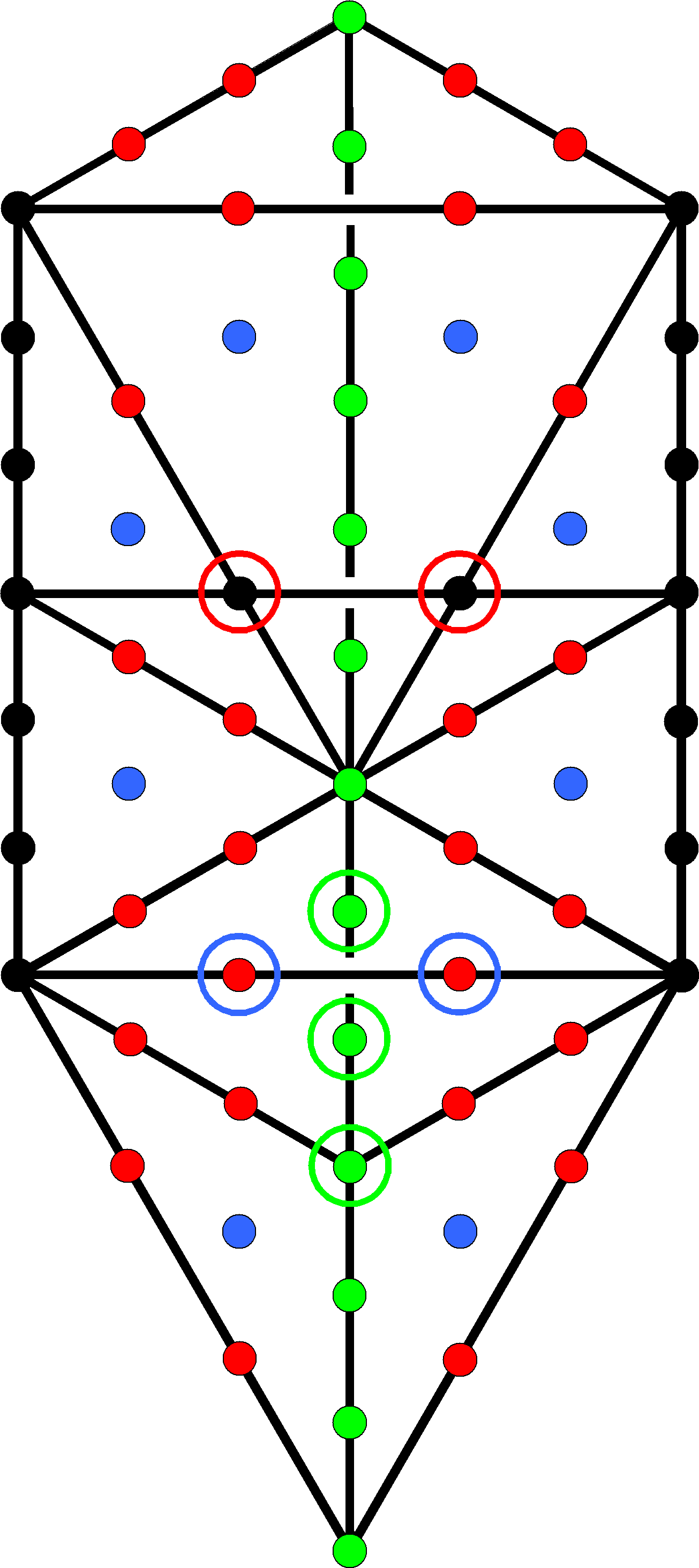 |
There are 16 green yods aligned with the central Pillar of Equilibrium. On either side of it are eight black yods, which are shared with the associated set of seven enfolded polygons in the inner Tree of Life, and five blue hexagonal yods at the centres of triangles, making a total of 42 yods. There are 14 red hexagonal yods on each side of the Pillar of Equilibrium that are intrinsic to the outer Tree of Life and which line sides of tetractyses. Hence, 70 = 42 + 28. |
Finally, consider case b. The trunk of the Tree of Life has 10 Paths (nine sides of five triangles and the Path connecting Chokmah and Binah). When they are Type A, the triangles add (5×3=15) sides, so that the trunk contains (10+15=25) sides. The branches of the Tree of Life has 12 sides of 11 triangles. When they are Type A, (11×3=33) sides are added, so that the branches contain (12+33=45) sides; this makes a total of (25+45=70) sides of the (16×3=48) triangles in the Tree of Life. Three of these sides are their own images when the mirror is aligned with the central Pillar of Equilibrium in a plane that is perpendicular to that containing the two side pillars. The branches have (45−3=42) sides that are not their own mirror images, i.e., 21 pairs of sides and their mirror images. There remain (25+3=28) sides that are either making up the trunk or belong to the branches as mirror images of themselves. Hence, 70 = 28 + 42, where 42 = 2×21.
42:28 division of 70 in the disdyakis
triacontahedron
Here are five examples of sacred geometries that embody not only the number 70 but also the number 42 as a natural
and complete subset of the 70 structural elements ("complete," that is, in the sense that no element of the same
class as that of any in the subset is excluded from the subset). This 28:42 division manifests as well in the
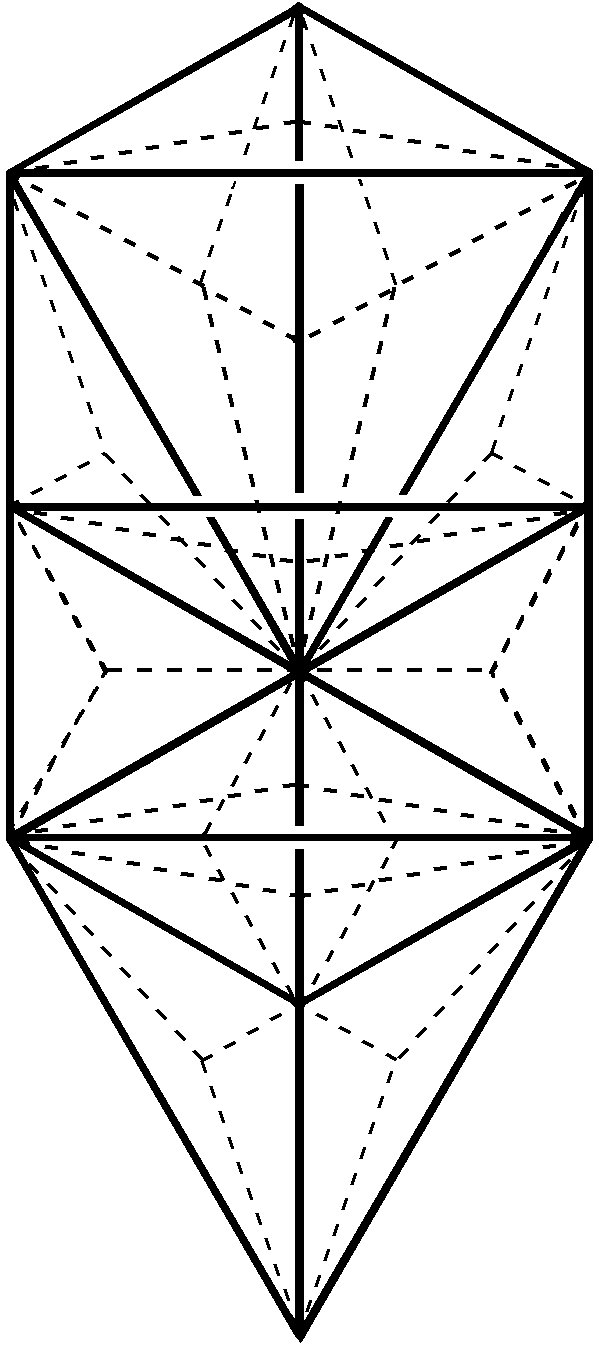
disdyakis triacontahedron, one of the two polyhedra that constitute the Polyhedral Tree of Life (see here). Its 62 vertices consist of 30 A
vertices, 12 B vertices and 20 C vertices. Projected onto a plane perpendicular to an axis passing through two
diametrically opposite C vertices, they form 15 layers of polygons, with these C vertices
either next below the top polygon or next above the lowest one (see here). There are 28 vertices and seven
centres of the polygons that are above the central, hexagon whose corners are all A vertices;
similarly, there are 28 vertices and seven centres for the similar set of polygons below the hexagon. In total,
there are 70 points either above or below its central plane:
28 + (7+7+28) = 70 = 28 + 42.
42 points consist of 28 vertices in one half of the polyhedron and the centres of the 14 polygons formed by vertices above and below the central plane. This leaves 28 vertices in the other half. Each set of 28 vertices consists of a single C vertex acting as the "pole" (although it is not the highest or lowest point in the polyhedron) and 27 vertices (12 A, 6 B & 9 C) that are the corners of five triangles and two 6-gons. It seems natural for the two C vertices to correspond to the bindu and the bottom corner of the central triangle in the Sri Yantra (and, in general, to the "2" in the sum 70 = 2 + 68 that characterises the 70 structural elements of the sacred geometries discussed above). However, this choice would mean that the set of 42 points cannot comprise all the centres of the 14 polygons and just the 28 vertices in one half of the polyhedron, as simple arithmetic might suggest. The 42:28 division has to arise in a way that preserves the mirror symmetry between the two sets of seven polygons. The numbers of centres & corners of polygons in either set of seven polygons (including its C vertex) are (in descending order from the top polygon):
4
1 (C)
7
4
7
4
4
4
(see here). The 34 points in each half other than the C vertex consist of five sets of four and two sets of seven:
34 = 5×4 + 2×7.
Therefore,
70 = 2×35 = 2(1+34) = 2 + 2×34 = 2 + 10×4 + 4×7 = 2 + 40 + 28 = 42 + 28.
The 10 triangles in the two halves generate 40 points, which form a set of 42 points when the two C vertices are included. The four 6-gons in the two halves generate 28 points. The 42:28 division in the 70 points emerges naturally from the differentiation between the triangles and the 6-gons formed by the vertices in the 14 layers above or below the central plane of the disdyakis triacontahedron. Notice how the factorisation of 28 as 4×7 is found in the pattern of 28 red corners of the outermost ring of 14 triangles in the 2-d Sri Yantra. The seven linked triangles in each half of the ring have 14 corners that consist of seven joined corners and seven unjoined corners. This means that the 28 corners of these 14 triangles comprise four sets of seven corners, just as 24 of the vertices of the disdyakis triacontahedron are the corners of four 6-gons, each of which has six sectors with seven corners. It illustrates how sacred geometries embody in their structural parameters the same pattern of numbers.
We have seen that the 6/5 ratio is the signature of the distinction between the trunk and branches of the outer Tree of Life, which manifest in its polyhedral form as the 72 vertices surrounding the axis of the 144 Polyhedron and the 60 vertices surrounding the axis of the disdyakis triacontahedron, where 72/60 = 6/5. The distinction is built into the geometry of the inner Tree of Life as well because 6n yods (5n hexagonal yods) surround the centre of a Type A n-gon constructed from tetractyses. It also appears in the Type B n-gon because, of the 15 yods per sector, 12 yods line sides of tetractyses, of which 10 are hexagonal yods, so that the ratio of the number of boundary yods to the number of such yods that are hexagonal yods = 12n/10n = 6/5. However, if one insists that the "6" and the "5" should refer to different sets of structural elements in order for the ratio 6/5 to be the signature of the presence of both trunk-like and branch-like patterns, then the "trunk" of a Type B n-gon is its 5n hexagonal yods when Type A and its "branches" are the 6n hexagonal yods lining its 3n tetractyses that are added by the transformation of the n-gon to Type B. The Type B dodecagon is the unique polygon whose trunk has 60 yods corresponding to the 60 vertices that surround an axis of the disdyakis triacontahedron and whose branches have 72 hexagonal yods lining 36 sides of 36 tetractyses that correspond to the 72 vertices surrounding an axis of the 144 Polyhedron. Each of the 14 polygons in the inner Tree of Life can be said to have its counterpart of the trunk and branches of the outer Tree of Life. But it must be remembered that the 6:5 proportion refers to the yod composition of polygons, whereas in the outer Tree of Life it refers to its geometrical composition (sides of triangles), whilst in the Polyhedral Tree of Life it refers to polyhedral vertices. When the seven separate Type A polygons become enfolded, their 295 yods become 264 yods, i.e., 31 yods disappear, where 31 is the number value of EL, the Godname of Chesed. The (3×48=144) yods lining their sides become 120 yods when they are enfolded, i.e., 24 yods disappear. Their (144+7=151) internal yods become 144 yods, i.e., seven yods disappear (five hexagonal yods and the centres of the hexagon and decagon). It is a testament to the amazing, mathematical design of the inner Tree of Life that the ratio of the numbers of boundary yods and internal yods of the seven enfolded polygons: 144/120 = 6/5, is the very proportion of sides of triangles in the branches (12) and trunk (10) of the outer Tree of Life: 12/10 = 6/5! Its counterpart in the Polyhedral Tree of Life is the ratio 72/60 = 6/5 between the numbers of vertices surrounding the axes of the 144 Polyhedron and the disdyakis triacontahedron. This is also the ratio of the numbers of their faces: 144/120 = 6/5, as well as the ratio of the numbers of their edges: 216/180 = 6/5.