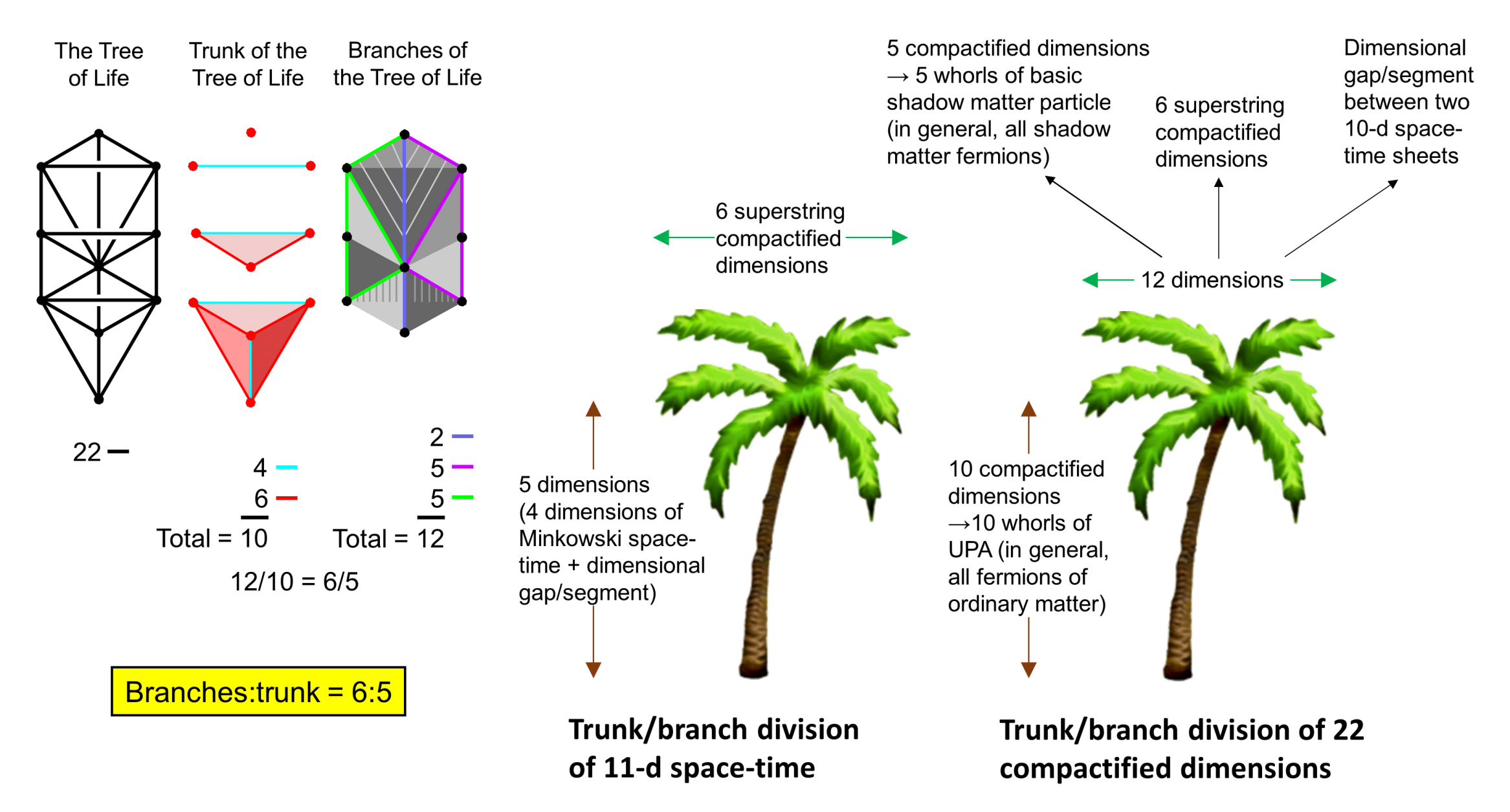
#5 Branch/trunk pattern of division in the space-time dimensions of the E₈×E₈′ heterotic superstring

The numbers of revolutions of each whorl in the basic unit of shadow matter (E₈-singlet state of the E₈×E₈′ heterotic superstring) and in its ordinary matter counterpart (E₈′-singlet, subquark state) are in the ratio 6/5. This ratio also applies to the total number of circular turns in each helical whorl because the number of turns per revolution is the same (namely, 336) for both types of basic particle (see #2). As the micro-physical realisation of the Tree of Life blueprint, the UPA is the trunk of the Tree of Life and the shadow matter particle is its branches. Just as equal numbers of geometrical elements can be associated with each half of the trunk or with each half of the branches, so the whorl in each particle has an equal number of revolutions and an equal number of turns in their outer and inner halves, although these numbers are different for the two particles, being 6/11 of the sum of these numbers in the case of the shadow matter particle and 5/11 of this sum in the case of the UPA. The number 11 in the denominator of these fractions suggests that any holistic parameter that is an integer multiple of 11 (say, 11N) is the sum of a number 5N that quantifies a trunk-like component of the system and a number 6N that quantifies its branches. An example of this is each half of the inner Tree of Life with 264 yods. As 264 = 11×24, 5/11 of 264 is (5×24=120), which is the number of yods lining the sides of the seven enfolded polygons, and 6/11 of 264 is (6×24=144), which is the number of their internal yods. Another example is the 3-d Sri Yantra, whose central bindu and 43 triangles consist of 88 points. 5/11 of 88 is 40, which is the number of points extending out to the second layer of triangles:

1 + 3 + 16 + 20 = 40,

and 6/11 of 88 is 48, which is the number of points in the third and fourth layers:

20 + 28 = 48.

Not all holistic parameters, of course, need to have 11 as a divisor, for they may quantify only a major component, i.e., not all, of the holistic system. However, according to M-theory, which unifies 11-d supergravity theories with 10-d superstring theories, space-time is 11-dimensional, whilst quantum mechanics requires spinless strings without supersymmetry to exist in a 26-d space-time with 22 compactified dimensions. Heterotic superstrings are a hybrid of these two types of strings, having a superstring component that propagates in 10-d space-time and a purely bosonic component that is 26-dimensional. Given that both 11 and 22 are exactly divisible by 11, let us see whether 5/11 and 6/11 of these numbers, namely, the numbers 5, 6, 10 & 12 have meanings vis-à-vis the space-times of superstring theory, M-theory and bosonic string theory.

M-theory predicts that 11-d space-time consists of Minkowski's 4-d space-time continuum, six curled-up, or "compactified," dimensions of space and another compactified dimension that is either a circle (SO(32) heterotic superstrings) or a line segment that extends a short distance along the tenth dimension of space predicted by M-theory (E₈×E₈′ heterotic superstrings). If we accept that the superstring is based upon the blueprint called "the Tree of Life" and its various isomorphic counterparts analysed in this website, then the 6-d space is its branches and the 5-d space-time that extends 4-d space-time into another dimension is its trunk (see the picture above). Now consider the 22 compactified dimensions predicted by string theory before supersymmetry is imposed on it to reduce this number to six. Does it not seem too much of a coincidence that the number of dimensions (15) beyond 11-d space-time just happens to be the same as the number of whorls in the two basic particles observed with micro-psi vision? Without going into mathematical details that would take us too far from the topic at hand, let us suppose that each one of these 15 whorls, which, as closed curves, are topologically equivalent to circles, is the result of some sort of deformation of a multi-dimensional object (called "branes" in the research literature) with respect to each one of these 15 compactified dimensions. In the case of the UPA, this deformation involves 10 dimensions, thereby generating its 10 whorls; these dimensions constitute the trunk of the Tree of Life pattern within both 11-d and 26-d space-times. For N whorls, each with 1680 turns (as in the UPA), the number of turns per E₈ gauge charge = 1680N/240 = 7N. For the UPA, the value of N is limited to 10 in order that each charge be parameterised by the number 70, namely, the number of yods in the complete Tree of Life. The remaining 12 compactified dimensions comprise the segment extending along the tenth dimension of space required by M-theory, the six compactified dimensions required by superstring theory and five compactified dimensions that are similarly responsible for the five whorls of the shadow matter particle (in other words, the brane in 26-d space-time gets turned into a fermion with either 10 or five whorls). These 12 dimensions constitute the branches of this pattern. The 22 Paths in the outer Tree of Life are sides of 16 triangles. They separate into the 10 Paths making up its trunk and the 12 Paths that are part of its branches. Their 6:5 division manifests in the (6+5=11) dimensions of space-time required by M-theory and in the (12+10=22) dimensions of space-time required by bosonic string theory. Both can exist only in the heterotic superstring. Superstrings of ordinary matter and shadow matter, as described with micro-psi by Annie Besant, C.W. Leadbeater and Ron Cowen, can co-exist only if they are E₈×E₈′ heterotic superstrings.

The trunk of the Tree of Life consist of 10 corners, 10 sides & five triangles; its branches consist of 12 sides & 11 triangles. If the gematria number value 168 of Cholem Yesodoth (חלם יסודות), the Mundane Chakra of Malkuth, is assigned to each one of its 22 Paths, the trunk embodies the number (10×168=1680) and the branches embody the number (12×168=2016):

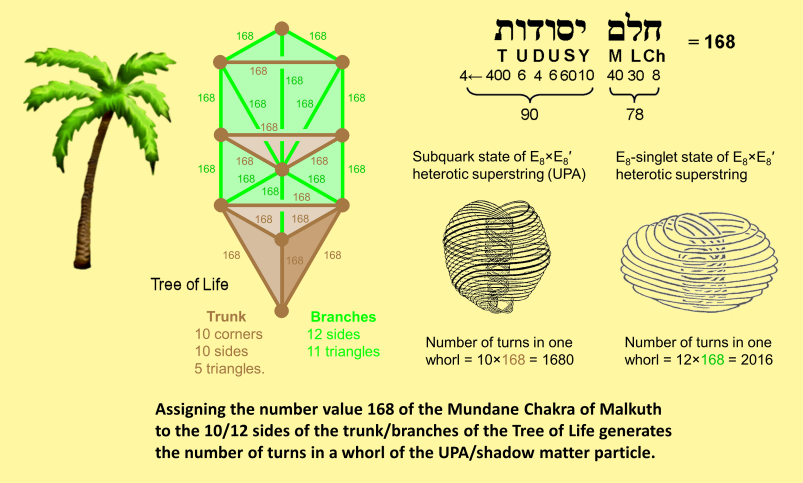
These numbers are the numbers of turns in one helical whorl of, respectively, the UPA and the shadow matter particle. As 168 is the number of turns in one half-revolution of a whorl of either particle, 1680 is the number of turns in 10 half-revolutions, i.e., five complete revolutions, which is what each whorl of the UPA makes, according to Besant & Leadbeater, whilst 2016 is the number of turns in 12 half-revolutions, i.e., six complete revolutions, which is what each whorl in the shadow matter particle makes, according to Ron Cowen (see page 2). Here is confirmation that he correctly counted the number of times the whorls twisted around the axis of the particle he examined with his micro-psi vision. To refute any criticism that circular logic undermines this claim, the reader is reminded that the number 2106 has been derived — not by making use of Cowen's observation (which would, indeed, amount to making a circular argument) — but in an independent way that makes no reference to it, namely, by hypothesizing that the 144 Polyhedron (the second member of the Polyhedral Tree of Life) represents the shadow matter particle, so that it embodies in its geometrical composition the number of turns in its whorl, just as the disdyakis triacontahedron does for the whorl of the UPA. We pointed out earlier that these two polyhedra can be regarded as the trunk and branches of the Polyhedral Tree of Life because the numbers of their vertices surrounding their axes are in the same ratio 6:5 as the number of Paths in the branches and trunk of the outer Tree of Life. Cowen had to count six revolutions in each whorl of the particle that he examined in order to reproduce the same ratio of 6:5. The fact that he did, as published in his book and therefore a matter of public record, testifies to the objectivity of his micro-psi vision. Anyone who disputes this by arguing that Cowen could have just "got lucky" is asking everyone else to believe in miracles of chance, wherein the same numbers are supposed to appear in several sacred-geometrical contexts always by coincidence!

<< Previous    1...   3  4  [5]  6  7  ...20    Next >>

Home