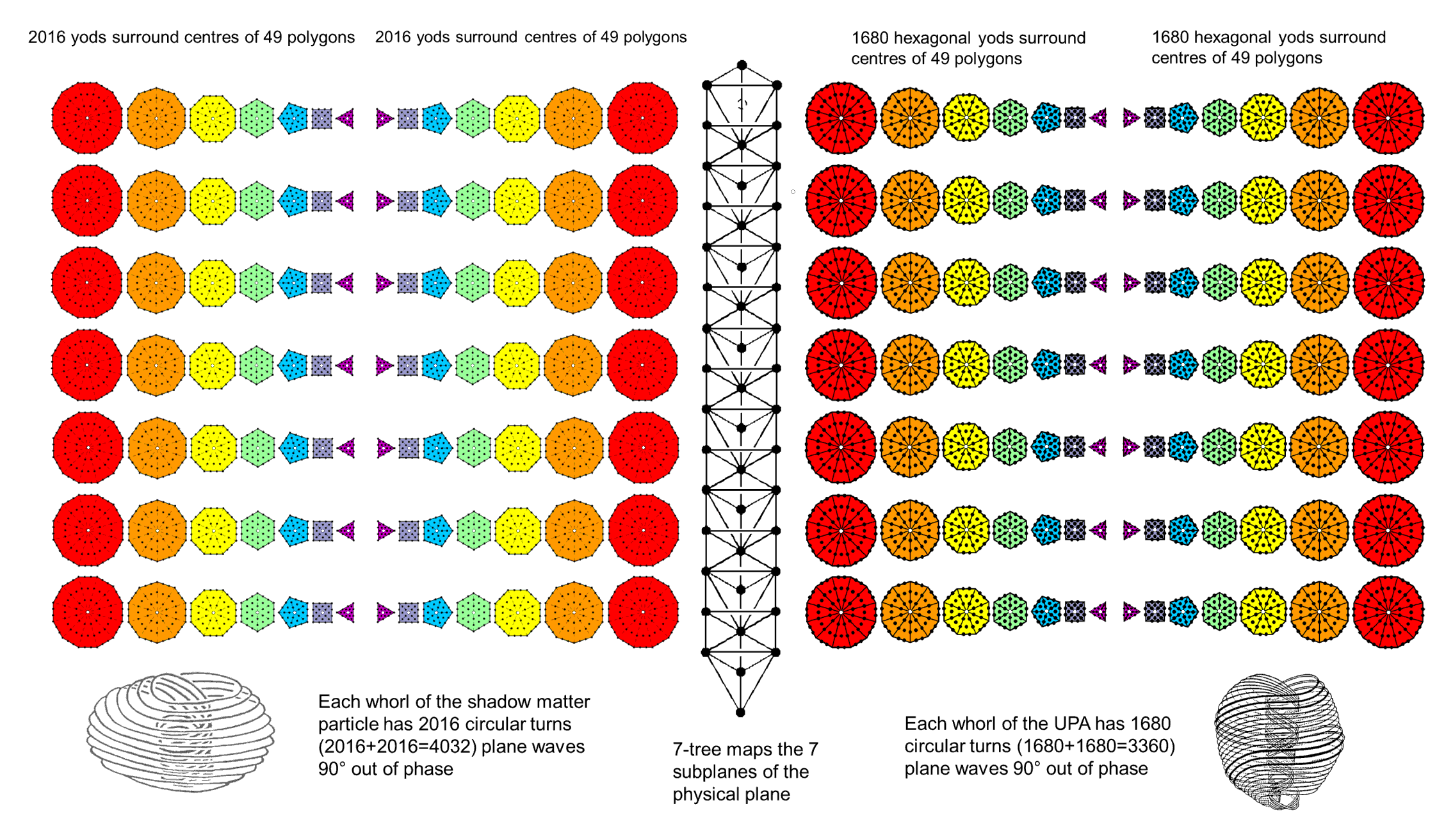
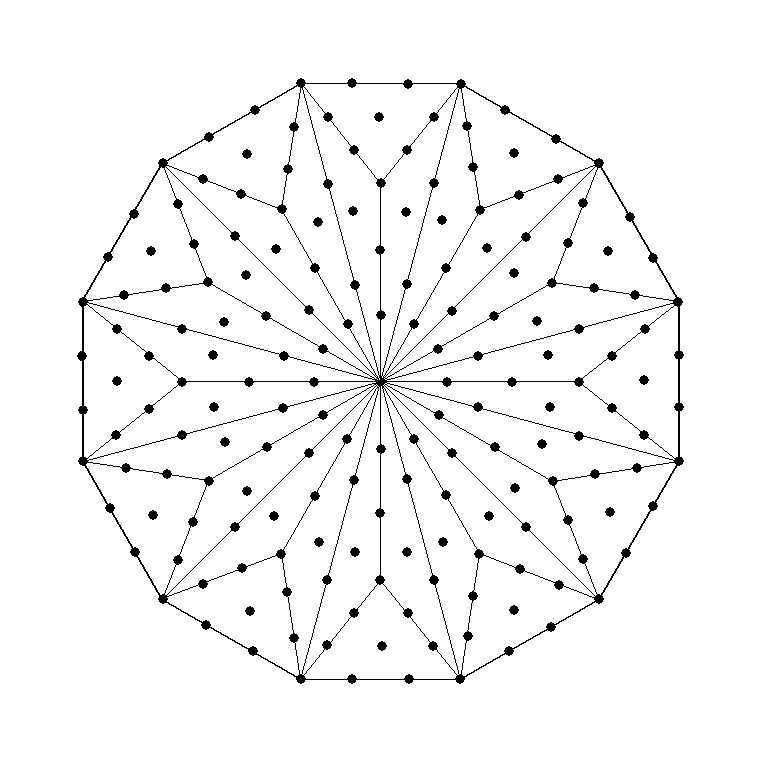
The inner Tree of Life basis of the whorl of either the basic shadow matter particle or the subquark of ordinary matter.
| << Previous 1... 5 6 [7] 8 9 ...23 Next >> |
#7 Outer/inner Tree of Life and polygonal encodings of the form of the shadow matter particle
The inner form of seven Trees of Life mapping the physical plane represents in a natural way the factorisations of the two superstring structural parameters 2016 and 1680:
2016 = 7×6×48,
1680 = 7×5×48.
The factor of 7 signifies the seven Trees, each corresponding to a Sephirah of Construction, the factor of 6 denotes the six yods per sector of a Type A polygon and the factor of 48 denotes the 48 sectors of the seven Type A polygons making up the inner form of each Tree. The factor of 5 denotes the five hexagonal yods per sector.
 |
|
The inner Tree of Life basis of the whorl of either the basic shadow matter particle or the subquark of ordinary matter. |
In the case of a shadow matter whorl, each of the six types of yods corresponds to a revolution, and the repetition of each type 48 times, then seven times, corresponds to the (48×7=336) turns in each revolution. For a whorl of the UPA, each of the five types of hexagonal yods corresponds to a revolution, and the repetition of each type 48 times, then seven times, corresponds to the 336 turns in each revolution. That is why the number of turns per revolution is the same for both types of whorl. The geometry of the inner Tree of Life requires this to be so. Its two enantiomorphic halves, each with 1680 hexagonal yods or 2016 yods, express the fact that each turn of a whorl is a circularly polarised oscillation made up of two perpendicular oscillations that are 90° (¼-cycle) out of phase with each other. Every yod in one half has its counterpart in the mirror-image half, and every one of the 1680 or 2016 pairs of yods symbolises a pair of oscillatory components that make up each of the 1680 or 2016 circularly polarised oscillations in a whorl.
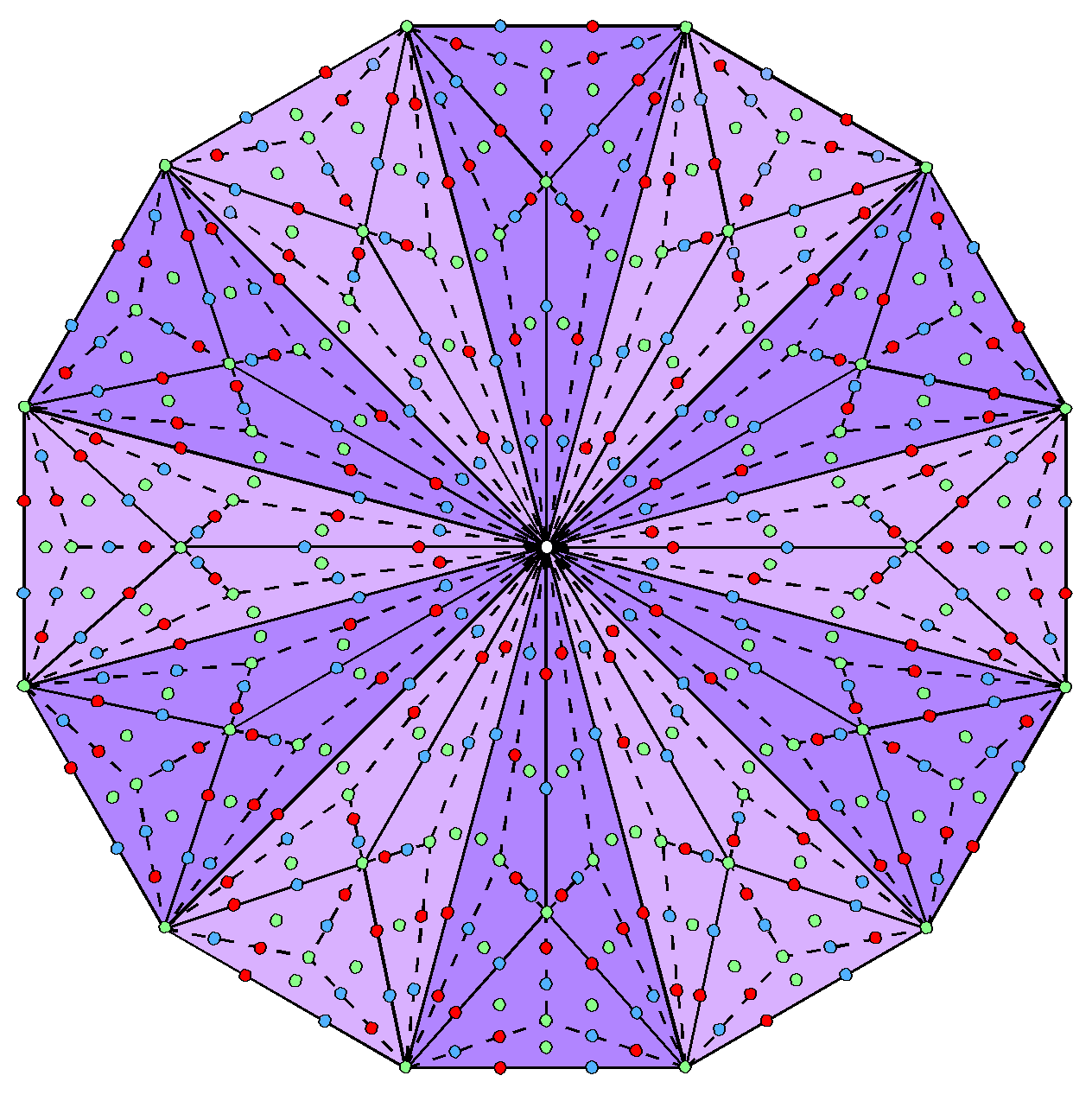
The representation shown above expresses the structure of a whorl from the perspective of each Sephirah of Construction, mapped by a Tree of Life. If we wish to portray the shadow matter particle or the UPA as they are in space-time, we need to absorb the external factor of 7 in the inner Tree of Life itself and choose a set of, respectively, five or 10 Trees of Life to map their five or 10 whorls. This can be done by choosing Type C polygons because the yod population of a Type C n-gon = 42n + 1, where 42 = 7×6. Below is shown the 2016 yods that surround the centres of the seven Type C polygons:
|
|
|
|
Notice how the 42 yods per sector form six sets of seven yods. Hence, the 48 Type B sectors of the seven Type C polygons comprise six sets of (7×48=336) yods. This corresponds to the six revolutions of a whorl, each having 336 turns. Notice also that the 14 yods per red, green & blue sector of each Type B triangle consist of seven yods of a darker shade and seven yods of a lighter shade of each primary colour. The six sets of seven yods comprise three sets of lighter coloured yods and three sets of darker coloured yods. This 3:3 division of sets corresponds to the three outer revolutions and the three inner revolutions of each spiralling whorl. As in the inner form of seven Trees, the pair of counterpart yods in each half of the inner Tree of Life symbolises the two transverse, orthogonal oscillations 90° out of phase that form each circular turn in a whorl. The (42+42) yods per pair of corresponding sectors of the polygons in each half of the inner Tree of Life express each non-zero root/gauge charge of the symmetry group E8′ governing the unified interactions of the shadow matter sector. In fact, when separated by the root edge, the two sets of seven Type C polygons have (248+248=496) corners of 864 tetractyses, where 248 is the number value of Raziel, the Archangel of Binah, and 496 is the number value of Malkuth:
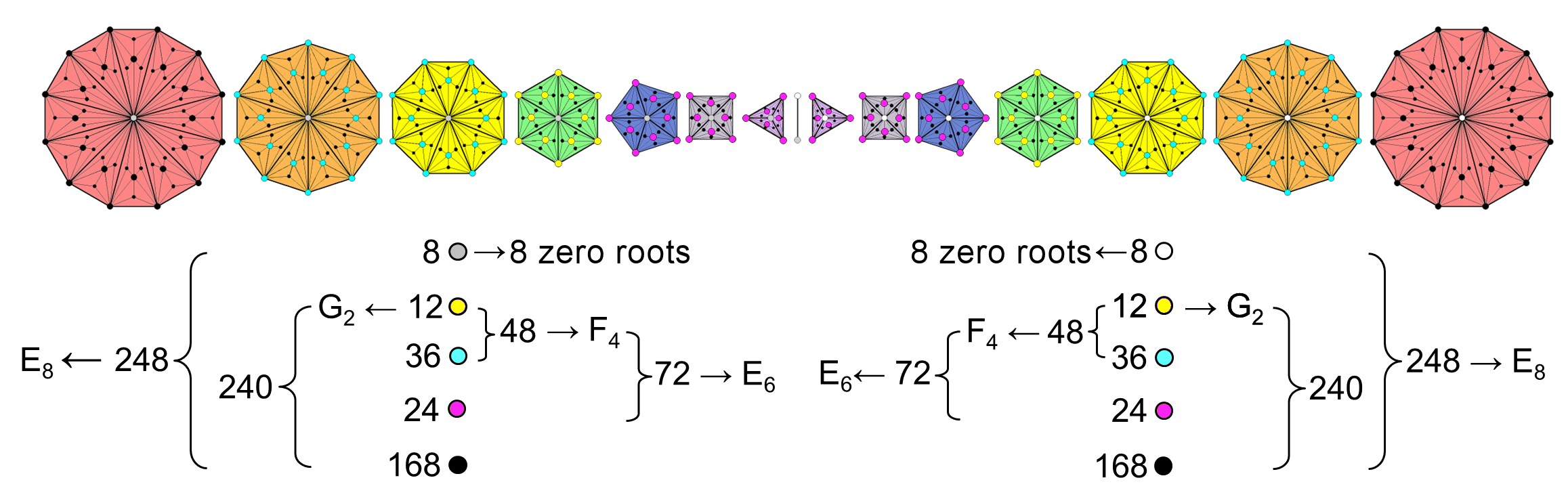 |
|
|
Both the structure and the unified dynamics of the shadow matter superstring conform to the blueprint of the inner Tree of Life.
The amazing
dodecagon
As the last of the seven regular polygons that make up the inner Tree of
Life, the dodecagon has properties that reflect its correspondence with Malkuth, the last of the seven
Sephiroth of Construction. It also has special Pythagorean significance because it is the
tenth regular polygon, and the ancient Pythagoreans taught that the progression of the integers is
completed with the number 4 because 1 + 2 + 3 + 4 = 10 and all other integers are different combinations of these
integers. The dodecagon symbolises the number 12, which is the tenth integer after 2, the Dyad and
the first prime number.
 |
 |
 |
 |
|
The dodecagon |
Weighted with the Tetrad (4), the 12 corners of the dodecagon generate the holistic parameter 48 as the number of corners of the 7 polygons of the inner Tree of Life, whilst the 60 hexagonal yods generate the number (240) of their hexagonal yods. Its 72 yods generate the total number (288) of yods. This is the musical number weight for which the Tetrahedral Lambda generates the structural parameters 10080 & 2016 of the shadow matter superstring and the structural parameters 1680 & 16800 of the subquark superstring (UPA). |
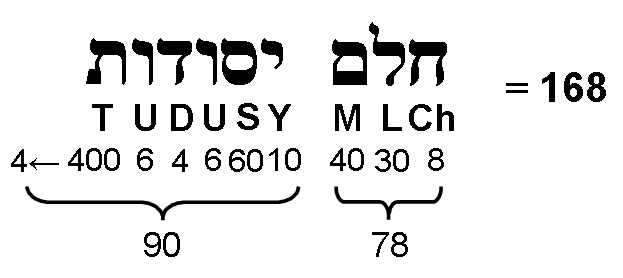
Weighted with the Tetrad, the 180 yods surrounding the centre of the Type B dodecagon generate the number (720) of yods in the 7 Type B polygons. 168 yods are needed to transform the dodecagon into the Type B dododecagon. 168 is the structural parameter of the subquark state of the E8×E8′ heterotic superstring. |
Weighted with the Tetrad, the 504 yods surrounding the centre of the Type C dodecagon generate the structural parameter 2016 of the shadow matter superstring. There are 504 SLs in CTOL, counting upwards from the apex of the 7-tree that maps the physical plane. 336 points, lines & triangles surround the centre of the Type C dodecagon. This is a structural parameter of both the shadow matter particle and the UPA, being the number of turns in one revolution of their helical whorls. |
The Type A dodecagon is the polygonal version of the Tree of Life (see here). Surrounding its centre are 72 yods, where 72 is the number value of Chesed, the first Sephirah of Construction, of which 60 are hexagonal yods. Every Type A polygon exhibits the 6:5 ratio expressed by the 12 straight lines in the branches of the outer Tree of Life and the 10 lines making up its trunk because an n-gon has 6n yods, of which 5n are hexagonal. What makes the dodecagon unique amongst polygons is: 1. when weighted with the Tetrad (4), its hexagonal yods generate the total number (240) of hexagonal yods in the seven types of polygons making up the inner Tree of Life, 2. its corners generate the total number (48) of their corners, so that all its weighted yods generate the number (288) of yods surrounding their centres. In other words, it generates the very musical number weight that — as we saw earlier — creates a Tetrahedral Lambda of 20 number weights whose sum is 16800 — the number of turns in the 10 helical whorls of the UPA — whilst 10 of them add up to 10080, which is the number of turns in the five whorls of the shadow matter particle. The reverse of this factorisation 288 = 72×4, namely, 288 = 4×72, appears in the square constructed from 2nd-order tetactyses, which has 288 yods surrounding its centre:
| 288 = |  |
It is an example of how the square — the symbol of the Pythagorean Tetrad — embodies holistic parameters (see Article 9 for how the square embodies the superstring structural parameter 168 and the dimension 248 of the exceptional Lie group E8 that expresses the symmetry of the unified forces between superstrings of ordinary matter, such as the UPA, or between superstrings of shadow matter, such as the particle described by Ron Cowen). The Type B dodecagon has 180 yods surrounding its centre. When weighted with the Tetrad, they generate the number (720) of yods in the seven Type B polygons. This is the number generated by assigning the Decad (10) to the 72 yods of the Type A dodecagon. Turning the latter into Type B requires 168 yods. This is the number of turns in a half-revolution of a whorl of either the shadow matter particle or the UPA. 168 is the gematria number value of Cholem Yesodoth, the Mundane Chakra of Malkuth:
Surrounding the centre of the Type C dodecagon are 504 yods. Weighted with the number 4, they generate the number of turns in a whorl of the shadow matter particle: 504×4 = 2016. The significance of the number 504 vis-à-vis CTOL is that there are 504 SLs down to the apex of the 7-tree mapping the physical plane made up of ordinary matter and shadow matter. This is because there are 47 SLs in the 7-tree, so that, given that CTOL has 550 SLs, its apex is the 504th SL. They comprise 168 SLs on each of the three pillars. The Type C dodecagon expresses this triple pattern because the 42 yods per sector consist of three natural sets of 14 yods (coloured red, green & blue in the diagram above), so that 504 = 12×42 = 12(14+14+14) = 168 + 168 + 168.
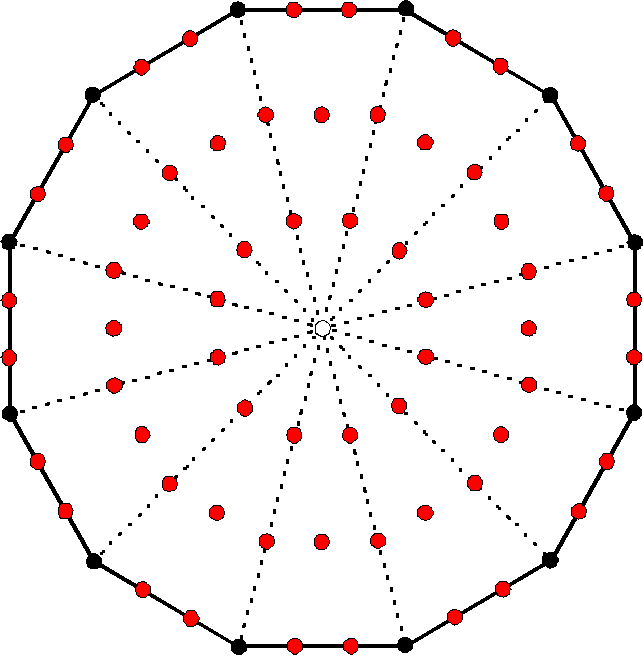
According to Table 9 in Article 65, the number of geometrical elements surrounding the centre of the nth-order m-gon = m(1+3n). The number of geometrical elements surrounding the centre of the Type C m-gon (n = 3) = 28m. For the Type C dodecagon (m = 12), (28×12=336) points, lines & triangles (168 points & triangles, 168 lines) surround its centre:
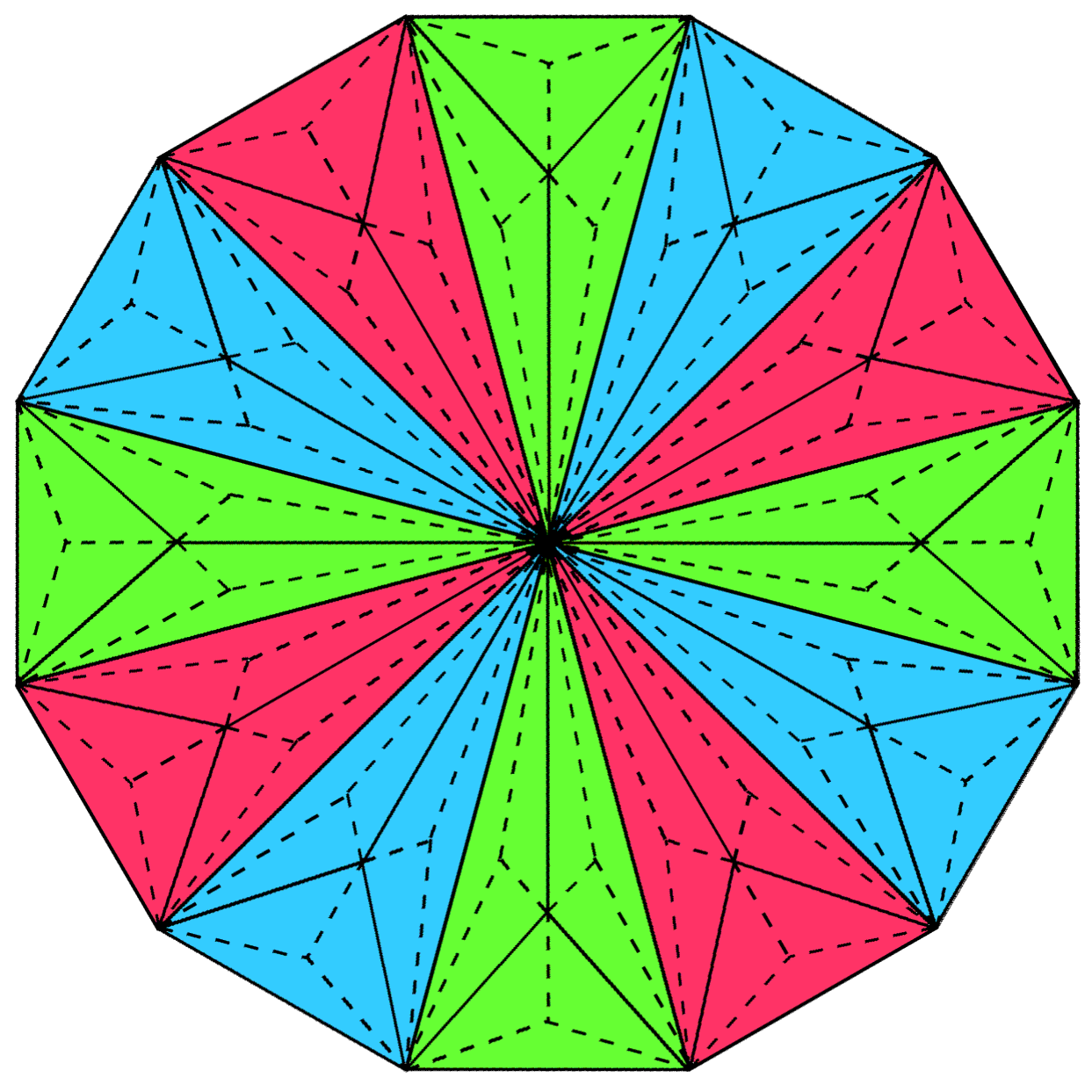 |
| 336 geometrical elements (168 corners & triangles and their 168 sides) surround the centre of the Type C dodecagon. |
This is how the geometry of the Type C dodecagon embodies the superstring structural parameter 336 (the number of turns in one revolution of a whorl). As 336/8 = 42, which is the number of turns over which one E8′ gauge charge is spread, a single revolution of a whorl of the shadow matter particle expresses eight such charges (48 charges per whorl). It is why the 240 gauge charges of E8′ require a superstring made out of 30 revolutions of five whorls. The Type C octagon has (8×42=336) yods surrounding its centre. The 48 sectors of the seven Type C polygons group naturally and uniquely into six sets of eight sectors, each set containing 336 yods:
triangle+pentagon: 8×42 = 1×336;
square+dodecagon: 16×42 = 2×336;
hexagon+decagon: 16×42 = 2×336;
octagon: 8×42 = 1×336;
Total = 6×336.
Each set becomes expressed in the helical whorl of the shadow matter superstring as a complete revolution composed of 336 turns. It has six revolutions because there are six sets equivalent to the octagon in terms of yod population. Alternatively, as was discussed above, the fact that the 42 yods per sector form six natural groups of seven yods means that the 2016 yods consist of six groups of (48×7=336) yods, each group being expressed by a revolution of a whorl comprising 336 turns. Which of these equally possible interpretations:
2016 = 48×42, where 48 = 6×8 and 42 = 6×7,
is the correct one, when both lead to the required factorisation 6×336? In other words, does the factor "6" expressing the number of revolutions originate in the factor "48" or in the factor "42"? The ambiguity arises simply because 2016 = 6×6×56. It also applies to the factorisation 7×6×48 discussed earlier for the seven Trees of Life mapping the physical plane, where the six revolutions could be ascribed to the 6×8 factorisation of 48 instead of to the six yods per Type A polygonal sector. The further factorisation of 6 into 2×3 (two halves of a whorl, each with three revolutions) does not help to decide between the two alternatives because the six yods consist of three boundary yods and three internal yods, whilst the six sets of eight sectors consist of three sets of eight sectors in the triangle, square, pentagon & dodecagon and three sets in the hexagon, octagon & decagon. So we have to choose between these two sections of the inner Tree of Life, each with 24 sectors, and the two sets of three groups of seven yods in a sector of a Type C polygon in the diagram shown earlier: seven light/dark red yods, seven light/dark green yods & seven light/dark blue yods. Previous work by the author (see Article 64) has shown that each half of the inner Tree of Life consists of two sets of polygons that are its two "halves" in the sense that they contain the same numbers of yods or geometrical elements — always when they are separate and sometimes as well when they are enfolded — after the question is settled as to which set the root edge shared by them all should be assigned. These two sets are those given above, namely, the triangle, square, pentagon & dodecagon with 24 corners and the hexagon, octagon & decagon with 24 corners. This bifurcation of the inner Tree of Life quantified by the number 48 into two halves, each quantified by the number 24 (which factorises as 8×3), is found in all holistic systems. An example is the row of eight trigrams and the column of eight trigrams in the I Ching table of 64 hexagrams whose intersection defines a hexagram as a pair of trigrams. It is sound reason why the inner and outer halves of each whorl in the shadow matter particle, which is mapped by the set of seven polygons in each half of the inner Tree of Life, should be identified with each natural half of this set. So the correct factorisation of the superstring structural parameter 2016 is 48×42, where 48 = 2×24 = 2×3×8. Each whorl makes six revolutions (three in each outer or inner half) because the seven polygons have 48 sectors that divide up into six sets of eight sectors (three sets in each "half" comprising either four or three polygons with 24 corners). A revolution corresponds to eight sectors that contain (8×42=336) yods, i.e., eight E8′ gauge charges. A sector of a polygon with 42 yods expresses a single E8′ charge. Because of the basic isomorphism between sectors of polygons and Trees of Life, the 48 sectors correspond formally to the 48 Trees of Life above the 1-tree that map the 48 subplanes of the cosmic physical plane "above" its lowest subplane. In 10-dimensional space-time mapped by 10 Trees of Life, they correspond to the 48 SLs spanned by the uppermost eight Trees that map the eight transverse dimensions of space. Two of these are large-scale and six are compactified, so that the 48 SLs comprise 12 SLs spanning the uppermost two Trees and 36 SLs spanning the next six Trees. This 12:36 division has its counterpart in the inner Tree of Life as the 12 sectors of the dodecagon and the 36 sectors of the first six polygons. Divided into its sectors, the dodecagon itself displays the division because its centre is surrounded by 12 points and 36 lines & triangles.
Finally, the relevance of the number 12 to the oscillatory form of the shadow matter superstring is both geometric and arithmetic. This is revealed by the arithmetic property that the number 168 of Cholem Yesodoth is the sum of the first 12 odd integers after 1:
132 − 1 = 168 = 3 + 5 + 7 + 9 +11 + 13 + 15 + 17 + 19 + 21 + 23 + 25,
so that the number of turns in each whorl of this superstring is
2016 = 12×168 = 36 + 60 + 84 + 108 + 132 + 156 + 180 + 204 + 228 + 252 + 276 + 300.
As this is the sum of an even number of evenly-spaced integers, the 1st & 12th, 2nd & 11th, etc numbers can be added together to create six identical numbers 336, i.e., 2016 = 6×336. We see that this arithmetic property reproduces the six revolutions, each with 336 turns (or 12 half-revolutions, each with 168 turns), of each helical whorl of the shadow matter superstring. As the ancient Pythagoreans taught, the forms taken by matter are the manifestation of numbers.
Article 10 analyses more properties of the dodecagon.
2106 as the 63rd triangular number
In earlier pages of this section, it was predicted
that each helical whorl of the basic unit of shadow matter has 2016 turns. This number can be factorised as 32×63.
The formula n(n+1)/2 for the sum of the first n integers:
1 + 2 + 3 +... + n = n(n+1)/2
yields this factorisation when n = 63, so that:
2016 = 1 + 2 + 3 +... + 63,
i.e., it is the 63rd triangular number.
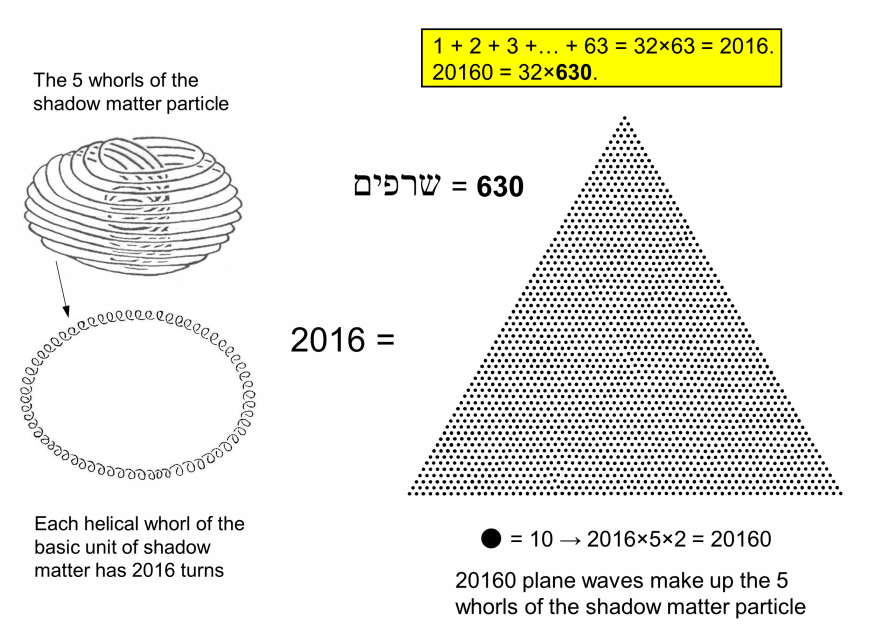
According to Ron Cowen, the shadow matter particle has five whorls. They should therefore comprise (5×2016=10080) turns. As circularly polarised waves, each one is the superposition of two perpendicular waves that oscillate 90 degrees out of phase with one another. The shadow matter particle comprises (10080×2=20160) plane wave oscillations. This number is generated by giving the weight of 10 to each of the 2016 dots present in the 63rd triangular number, as shown above. The sum of the 63 weighted dots on each side of the triangular array is 630. This is the number value of Seraphim (שרפים), meaning "Flaming Serpents" (Isaiah 6:6), the Order of Angels associated with Geburah.
| << Previous 1... 5 6 [7] 8 9 ...23 Next >> |