ARTICLE 10

by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth.
Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
The dodecagon has Pythagorean significance vis-à-vis the
perfect number 10 because it is the tenth regular polygon.
It is also the last of the seven regular polygons constituting the inner
form of the Tree of Life. This article confirms the special status of the
dodecagon by showing how it geometrically embodies in a natural way the
numbers 168, 336 & 1680 characterising the 3-dimensional form of the
superstring constituent of up and down quarks and the number 248
characterising their unified dynamics. The number values of the Godnames of
the ten Sephiroth are shown to prescribe properties of a single dodecagon
and a pair of joined dodecagons, thus indicating that they constitute
‘sacred geometry’ and must embody numbers of universal significance, such as
these defining parameters of superstrings. This conclusion is confirmed by
the simple and beautiful way in which the Pythagorean Tetrad expresses their
properties. As the last member of the set of seven regular polygons, the
dodecagon corresponds to Malkuth, the seventh and last Sephirah of
Construction, because it embodies information about the ‘Malkuth’ or
objective aspect of the microscopic manifestation of the Tree of Life in
space-time. Being the polygonal counterpart of the Tree of Life, it has
analogous properties, some of which will be explored in later articles. Both
the yod population of the pair of joined dodecagons and the geometrical
composition of the separate pair manifest the 84:84 division that
characteristic of holistic systems. It is realised in the superstrings
making up the quarks in atomic nuclei as the 840 circularly polarised
oscillations in the outer or inner halves of each of their ten standing
waves.
|
1
Table 1. Number values of the ten Sephiroth in
the four Worlds.
|
|
SEPHIRAH
|
GODNAME
|
ARCHANGEL
|
ORDER OF ANGELS
|
MUNDANE CHAKRA
|
| 1 |
Kether
(Crown)
620
|
EHYEH
(I am)
21
|
Metatron
(Angel of the
Presence)
314
|
Chaioth ha Qadesh
(Holy Living
Creatures)
833
|
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
636
|
| 2 |
Chokmah
(Wisdom)
73
|
YAHWEH, YAH
(The Lord)
26,
15
|
Raziel
(Herald of the
Deity)
248
|
Auphanim
(Wheels)
187
|
Masloth
(The Sphere of
the Zodiac)
140
|
| 3 |
Binah
(Understanding)
67
|
ELOHIM
(God in multiplicity)
50
|
Tzaphkiel
(Contemplation
of God)
311
|
Aralim
(Thrones)
282
|
Shabathai
Rest.
(Saturn)
317
|
| |
Daath
(Knowledge)
474
|
|
|
|
|
| 4 |
Chesed
(Mercy)
72
|
EL
(God)
31
|
Tzadkiel
(Benevolence of God)
62
|
Chasmalim
(Shining Ones)
428
|
Tzadekh
Righteousness.
(Jupiter)
194
|
| 5 |
Geburah
(Severity)
216
|
ELOHA
(The Almighty)
36
|
Samael
(Severity of God)
131
|
Seraphim
(Fiery Serpents)
630
|
Madim
Vehement
Strength.
(Mars)
95
|
| 6 |
Tiphareth
(Beauty)
1081
|
YAHWEH ELOHIM
(God the Creator)
76
|
Michael
(Like unto God)
101
|
Malachim
(Kings)
140
|
Shemesh
The Solar Light.
(Sun)
640
|
| 7 |
Netzach
(Victory)
148
|
YAHWEH SABAOTH
(Lord of Hosts)
129
|
Haniel
(Grace of God)
97
|
Tarshishim or
Elohim
1260
|
Nogah
Glittering
Splendour.
(Venus)
64
|
| 8 |
Hod
(Glory)
15
|
ELOHIM SABAOTH
(God of Hosts)
153
|
Raphael
(Divine
Physician)
311
|
Beni Elohim
(Sons of God)
112
|
Kokab
The Stellar Light.
(Mercury)
48
|
| 9 |
Yesod
(Foundation)
80
|
SHADDAI EL CHAI
(Almighty Living God)
49,
363
|
Gabriel
(Strong Man of
God)
246
|
Cherubim
(The Strong)
272
|
Levanah
The Lunar Flame.
(Moon)
87
|
| 10 |
Malkuth
(Kingdom)
496
|
ADONAI MELEKH
(The Lord and King)
65,
155
|
Sandalphon
(Manifest
Messiah)
280
|
Ashim
(Souls of Fire)
351
|
Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168
|
|
The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah
and Assiyah. Corresponding to them are the Godnames, Archangels, Order of
Angels and Mundane Chakras (their physical manifestation). This table gives
their number values obtained by the ancient practice of gematria, wherein a
number is assigned to each letter of the alphabet, thereby giving a number
value to a word that is the sum of the numbers of its letters.
|
2
1.
Introduction
In earlier articles, analysis of the sacred geometry of the Tree of Life
uncovered properties quantified by numbers that are the 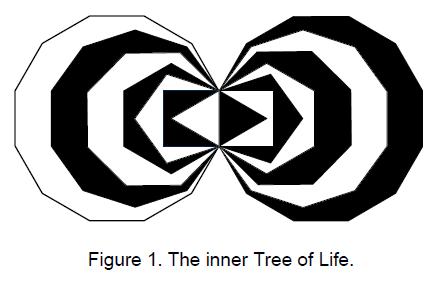 gematria number values of the ten Sephiroth, their Godnames, Archangels,
Orders of Angels & Mundane Chakras (Table 1). It was shown in Article 9 (1) that the square embodies the structural parameter 1681 and the dynamical parameter 248 of
the superstring constituent of up and down quarks (the latter embodiment was also discussed
in Article 1 (2)). Although the relevance of these numbers to the physics of the universe
was, of course, unknown to the early Pythagoreans, it illustrates in a remarkable way their
profound intuition about the fundamental importance of the number 4 to the study of the
natural world. This principle, which the author has called the “Tetrad Principle,” was
formally postulated in Article 1. But the number 10 was also central to Pythagorean
mathematics because it was symbolised as the fourth triangular number by the
tetractys: gematria number values of the ten Sephiroth, their Godnames, Archangels,
Orders of Angels & Mundane Chakras (Table 1). It was shown in Article 9 (1) that the square embodies the structural parameter 1681 and the dynamical parameter 248 of
the superstring constituent of up and down quarks (the latter embodiment was also discussed
in Article 1 (2)). Although the relevance of these numbers to the physics of the universe
was, of course, unknown to the early Pythagoreans, it illustrates in a remarkable way their
profound intuition about the fundamental importance of the number 4 to the study of the
natural world. This principle, which the author has called the “Tetrad Principle,” was
formally postulated in Article 1. But the number 10 was also central to Pythagorean
mathematics because it was symbolised as the fourth triangular number by the
tetractys:
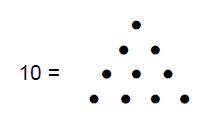
The dots will be called “yods,” after the name (yod) of the tenth letter (י)
of the Hebrew alphabet, which is somewhat shaped like a dot or point. The inner form of the
Tree of Life (Fig. 1) comprises seven enfolded, regular
polygons: triangle, square, pentagon, hexagon, octagon, decagon & dodecagon. The last of
these is the tenth regular polygon, counting from the simplest one — the
triangle. Given the titles “All Perfect,” “God,” & “Kosmos” given by the Pythagoreans to
the number 10, which they regarded as the perfect completion of number, it should come as no
surprise that the
dodecagon, too, embodies numbers of universal (and therefore scientific)
significance. This article discusses how the dodecagon encodes the numbers 168, 248, 336
and 1680 as parameters of the structure and dynamics of superstrings. Of these numbers, only
the second — the dimension of the rank-8, exceptional Lie group E8 used in
superstring theory — has as yet been recognised by particle physics. According to Table 1, it is the number value of
Raziel, the Archangel of Chokmah.
2. Properties of
the dodecagon
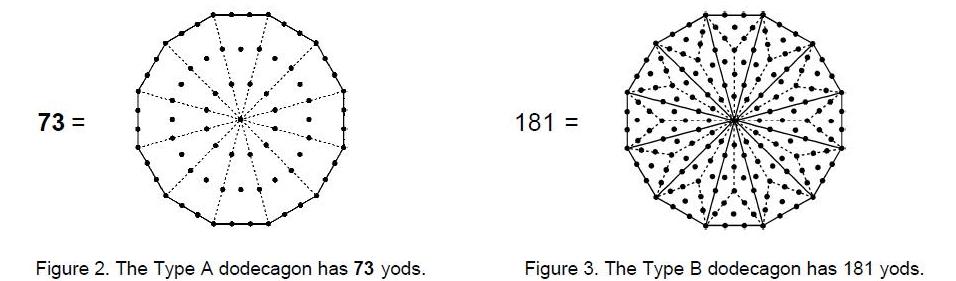
With its 12 sectors turned into 12 tetractyses, the dodecagon is made up of
73 yods (Fig. 2), of which
36 yods are on the boundary and 72 yods surround
its centre. 73 is the number value of Chokmah, the second member of
the Supernal Triad at the head of the Tree of Life, 36 is the Godname
number of Geburah, the fifth Sephirah from the top, and 72 is the
number value of Chesed, the fourth Sephirah from the top (see Table 2 below). The fact that a
Godname — ELOHA — prescribes the shape of the dodecagon by quantifying how
many yods are needed to mark out its boundary is the first sign that the dodecagon
constitutes ‘sacred geometry.’ A dodecagon whose sectors are triangles or tetractyses
(Fig. 2) will be called ‘Type A.’ A
dodecagon whose sectors are divided into three triangles or tetractyses (Fig. 3) will be called ‘Type B.’ This
type contains 181 yods (3). Corresponding nomenclature will apply
to all other polygons.
______________________
1 All numbers belonging to this table will be written in
boldface.
3
Rather than give tedious calculations, the properties of both types of
dodecagon are listed below for later discussion. For the sake of reference, the number values
of the Sephirothic titles, their Godnames, Archangelic Names, Angelic Names and Mundane Chakras
are shown in the following table. Numbers in coloured cells either have been already referred
to or will appear in later discussion.
Table 2. Gematria number values.
|
Sephirah
|
Title
|
Godname
|
Archangel
|
Order of
Angels
|
Mundane
Chakra
|
|
Kether
|
620
|
21
|
314
|
833
|
636
|
|
Chokmah
|
73
|
15, 26
|
248
|
187
|
140
|
|
Binah
|
67
|
50
|
311
|
282
|
317
|
|
Chesed
|
72
|
31
|
62
|
428
|
194
|
|
Geburah
|
216
|
36
|
131
|
630
|
95
|
|
Tiphareth
|
1081
|
76
|
101
|
140
|
640
|
|
Netzach
|
148
|
129
|
97
|
1260
|
64
|
|
Hod
|
15
|
153
|
311
|
112
|
48
|
|
Yesod
|
80
|
49
|
246
|
272
|
87
|
|
Malkuth
|
496
|
65, 155
|
280
|
351
|
168
|
Properties of: dodecagon; two separate dodecagons; joined dodecagons (4)
(Non-bracketed numbers refer to the Type A dodecagon; bracketed numbers refer to the Type B
dodecagon)
1. Number of corners of dodecagon = 12 (12) ; 24 (24); 22 (22).
2. Number of sides of dodecagon = 12 (12) ; 24 (24); 23 (23).
3. Number of corners & sides of dodecagon = 24 (24); 48
(48); 45 (45).
4. Number of triangles = 12 (36); 24 (72); 24
(72).
5. Number of corners of triangles = 13 (25); 26 (50); 24
(48).
6. Number of sides of triangles = 24 (60); 48 (120); 47 (119).
7. Number of corners & sides of triangles = 37 (85); 74 (170); 71 (167).
8. Number of sides & triangles = 36 (96); 72 (192); 71
(191).
9. Number of corners & triangles = 25 (61); 50 (122); 48
(120).
10. Number of corners, sides & triangles = 49 (121); 98 (242);
95 (239).
11. Number of corners, sides & triangles outside root edge = 46 (118); 95
(239); 92 (236).
12. Number of yods = 73 (181), 146 (362), 142 (358). Number of yods other than
centres = 72 (180); 144 (360); 140 (356).
13. Number of yods outside root edge = 69 (177); 138 (354); 138 (354).
14. Number of hexagonal yods = 60 (156); 120 (312); 118 (310).
15. Number of hexagonal yods outside root edge = 58 (154); 116 (308); 116 (308).
16. Number of yods on boundaries of dodecagon = 36 (36); 72
(72); 68 (68). Number of boundary yods outside root edge = 32 (32) ;
68 (68); 64 (64).
17. Number of internal yods = 37 (145); 74 (290); 74 (290).
18. Number of yods on sides of tetractyses = 61 (145); 122 (290); 118 (286). Number of yods on
sides of tetractyses outside root edge = 57 (141); 118 (286); 114 (282).
19. Number of yods on sides of tetractyses other than corners & centre of dodecagon =
48 (132); 96 (264);
94 (262). Number of such yods outside root edge = 46 (130); 92 (260); 92 (260).
20. Number of yods other than corners & centre of dodecagon = 60 (168);
120 (336); 118 (334).
21. Number of yods other than corners of dodecagon & centres of its sectors =
49 (157); 98 (314); 96 (312). Number of such yods outside root edge = 47
(155); 94 (310); 94 (310).
22. Number of yods other than corners of dodecagon = 61 (169); 122 (338); 120 (336).
Set out below are the ways in which the Godname numbers prescribe these
properties of the dodecagon and two separate or joined dodecagons:
| Kether: 21 |
21 corners & sides of dodecagon outside the root edge.
The Type A dodecagon has 73 yods, where
73 = 21st prime number. Also, 121
corners, sides & triangles in the Type B dodecagon, where
|
4
| |
121 = 112 = 1 + 3 + 5 + … +
21
is the sum of the first ten odd integers after 1. The
Pythagorean measure of perfection — the number 10 — therefore defines the
geometrical composition of the tenth regular polygon. The Decad
determines not only the number value 73 of Chokmah but also
the number value 67 of Binah because the tenth integer after 1
is 11 and an undecagon constructed from tetractyses has 67 yods. These
two number values have a remarkable connection to the geometry of what in
earlier articles was called

the “1-tree.” An n-tree (n an integer) is defined as the n
lowest trees of any set of N overlapping Trees of Life (n<N). Below Binah in
the 1-tree constructed from 19 tetractyses are 67 yods (Fig. 4). There are 73 yods up to the Path joining
Binah and Chokmah. Far from being arbitrary appellations, the Kabbalistic
titles of the Sephiroth have a geometrical basis vis-à-vis the Tree of Life
and any equivalent geometrical object that embodies the divine, mathematical
paradigm.
|
Chokmah: 15
26 |
47 sides of Type A dodecagon, where 47 = 15th
prime number. This is the number of sectors of the seven enfolded polygons of the
inner Tree of Life (Fig. 1).
Two separate, Type A dodecagons have 24 sectors with 26
corners. Also, number of yods outside the root edge on sides of
72 tetractyses in two
joined, Type B dodecagons which are not corners or centres of dodecagons = 260
= 26×10.
|
|
Binah: 50 |
Two separate, Type B dodecagons have 72 triangles
with 50 corners.
|
| Chesed: 31 |
Number of hexagonal yods in two joined, Type B dodecagons = 310 =
31×10. This is also the number of yods outside the root edge of
two joined,
Type B dodecagons other than the corners and centres of their sectors.
|
| Geburah: 36 |
Number of yods on boundary of dodecagon. Also, 36
is the number of triangles in the Type B dodecagon.
|
| Tiphareth: 76 |
Number of hexagonal yods outside root edge of Type B dodecagon =
154 = 77th even
|
5
|
|
integer. 77 = 76th integer after 1. |
| Netzach: 129 |
Number of
yods outside root edge on sides of 36 tetractyses other than
corners or centre of Type B dodecagon = 130 = 129th integer after
1. |
|
Hod: 153 |
Number of
hexagonal yods outside root edge of Type B dodecagon = 154 = 153rd
integer after 1. |
|
Yesod: 49 |
Number of
corners, sides & triangles of Type A dodecagon =
49. |
| Malkuth: 65 |
Number of
yods outside root edge on sides of tetractyses other than corners and centre of
Type B dodecagon = 130 = 65th even integer. |
|
155
|
155 hexagonal yods associated with each joined, Type B dodecagon. Also,
the number of yods outside the root edge of the Type B dodecagon other than its
corners and centres of its sectors. |
3. Encoding of superstring structural parameter
168
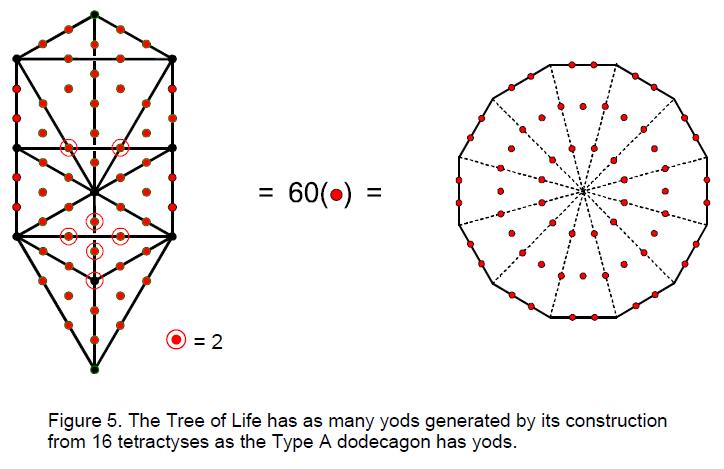
The Type A dodecagon has 60 yods other than corners surrounding
its centre (Fig. 5), whilst the Type B dodecagon has 168 yods other
than corners surrounding its centre (Fig. 6). In other words, 168 new yods are needed to
transform its sectors into tetractyses. Compare this with what was found for the square in
Article 9 (5): the Type B square with three tetractyses as each sector has 60 yods
surrounding its centre, whilst the Type C square with nine tetractyses as each 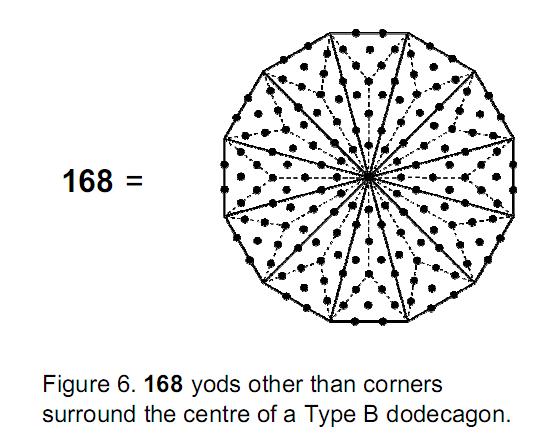 sector has 168 yods surrounding its centre. Polygons of
Type A, B, C, etc represent successive levels of complexity in their construction from
tetractyses. What is so remarkable and significant in the context of the special emphasis
given by the Pythagoreans to the Decad and to the Tetrad symbolised by the square is that
both the square and the tenth regular polygon embody the same pair of
numbers, although differently. 168 is just the number of extra yods
required to turn the twelve sectors of a dodecagon into tetractyses. In the case of the
outer form of the Tree of Life, there are 60 extra yods needed to construct it from
tetractyses. The dodecagon bears to the first six polygons the same relation as Malkuth
bears to the six higher Sephiroth of Construction. This is suggested by the fact that it
contains as many hexagonal yods as the Tree of Life — only its skeletal (Malkuth) boundary
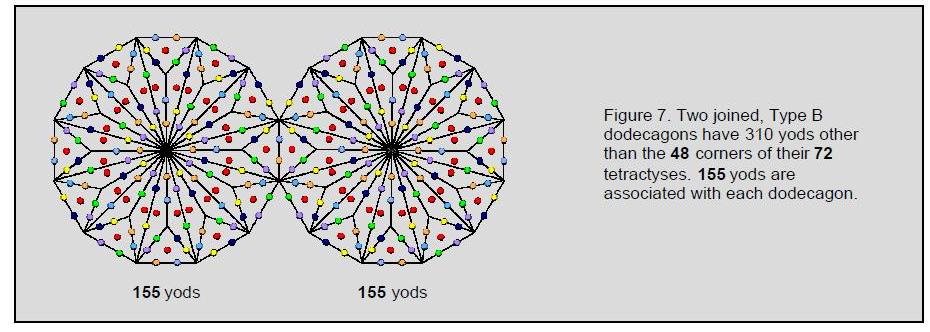
is different. It is confirmed by the fact that there are
155 hexagonal yods associated with each of the two joined, Type B
dodecagons (Fig. 7), whilst it has 168 yods other than corners of
its sectors, where 155 is the number value of ADONAI MELEKH, the
Godname of Malkuth, and 168 is the number value of Cholem
Yesodoth, the Mundane Chakra of this Sephirah. EL, the Godname of Chesed, prescribes
the pair of joined dodecagons because they contain
(155+155=310=31×10) hexagonal yods, where
31 is its number value. sector has 168 yods surrounding its centre. Polygons of
Type A, B, C, etc represent successive levels of complexity in their construction from
tetractyses. What is so remarkable and significant in the context of the special emphasis
given by the Pythagoreans to the Decad and to the Tetrad symbolised by the square is that
both the square and the tenth regular polygon embody the same pair of
numbers, although differently. 168 is just the number of extra yods
required to turn the twelve sectors of a dodecagon into tetractyses. In the case of the
outer form of the Tree of Life, there are 60 extra yods needed to construct it from
tetractyses. The dodecagon bears to the first six polygons the same relation as Malkuth
bears to the six higher Sephiroth of Construction. This is suggested by the fact that it
contains as many hexagonal yods as the Tree of Life — only its skeletal (Malkuth) boundary
is different. It is confirmed by the fact that there are
155 hexagonal yods associated with each of the two joined, Type B
dodecagons (Fig. 7), whilst it has 168 yods other than corners of
its sectors, where 155 is the number value of ADONAI MELEKH, the
Godname of Malkuth, and 168 is the number value of Cholem
Yesodoth, the Mundane Chakra of this Sephirah. EL, the Godname of Chesed, prescribes
the pair of joined dodecagons because they contain
(155+155=310=31×10) hexagonal yods, where
31 is its number value.
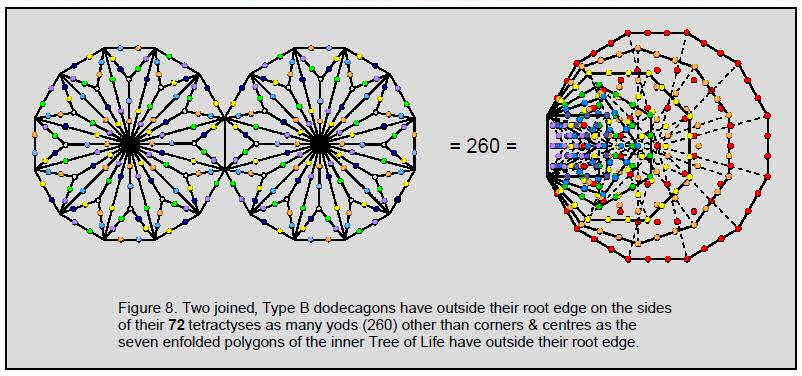
Further remarkable confirmation that the dodecagon constitutes sacred
geometry because its properties are prescribed by Godnames is the fact that, outside their root
edge, the two joined, Type B dodecagons
6
contain 260 (=26×10) yods on the sides of their
72 tetractyses that are not their 48 corners or centres,
where 26 is the number value of YAHWEH, the Godname of Chokmah. Compare this
with the fact that the seven enfolded, regular polygons contain 260 yods outside their shared
root edge (Fig. 8). In the first case, this number is that needed to delineate the edges
of their tetractyses outside the root edge, given their corners and centres; in the second
case, it is the number of yods required to construct the seven enfolded polygons, starting
with the root edge. The ways in which the generative Godname YAHWEH prescribes both
geometrical objects are analogous.
It is not coincidental that the two objects possess properties that are
quantified by the same sets of numbers listed in Table 2. The dodecagon is the polygonal form of the Tree of Life and will —
like any other holistic structure — embody the numbers listed in this table.
4. Encoding of
1680 in pair of joined dodecagons
It was shown in Article 9 that, when the yods in a square constructed from
tetractyses are themselves replaced by tetractyses (Fig. 9):
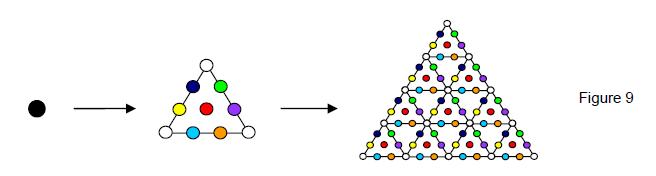
there result 248 yods other than corners of tetractyses,
that is, yods symbolising the seven Sephiroth of Construction. These symbolise the
248 quantum states of the particle transmitting the unified superstring force
described by the gauge symmetry group E8. A dodecagon with its 12 sectors turned
into such higher-order tetractyses contains 120 tetractyses, where
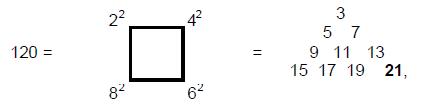
showing how the Tetrad determines this number. The number of yods in each
sector is
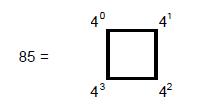
7

8
again illustrating the role of the Tetrad. Taking into account that 12 yods
on each internal edge of a sector apart from the centre of the dodecagon are shared with
adjoining sectors, there are (84–12=72) yods per sector, where
72 is the number of Chesed, the fourth Sephirah from the top of the
Tree of Life. Of these, 10 (=1+2+3+4) are corners of tetractyses symbolising Kether, Chokmah
and Binah and 62 are hexagonal yods symbolising Sephiroth of
Construction, where 62 is the number value of Tzadkiel, the
Archangel corresponding to Chesed. Therefore, the number of yods in the 120 tetractyses of a
dodecagon = 12×72 + 1 = 865. 13 yods lie along the shared edge of the
pair of dodecagons, leaving (865–13=852) yods outside it. The number of yods in the
dodecagon outside the root edge that surround the centres of each sector = 852 – 12 =
840,

where

and
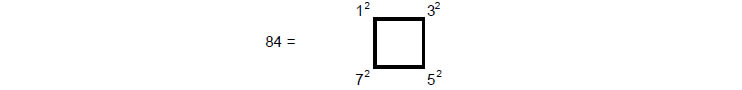
yet again illustrating the basic role of the Tetrad in defining properties
of sacred geometry with universal significance (as will become evident shortly). A pair of
joined dodecagons therefore has (840+840=1680) yods outside their shared edge that surround the
centres of their 24 sectors, where 24 = 1×2×3×4 (Fig. 10). This is the number of turns in each of the ten helical whorls
(Fig. 11) of the ‘ultimate physical atom,’ or UPA (Fig. 12), observed over 100 years ago by the two Theosophists Annie Besant
and C.W. Leadbeater, using a siddhi, or psychic ability, known to Indian yoga. Each whorl
makes 2½ outer revolutions about the vertical axis of spin of the UPA and 2½ inner
revolutions, spiralling 840 times in circles in each half. We see that each dodecagon
containing 840 yods distributed outside the root edge about the centres of its sectors
encodes the number of coils in half a whorl; the two identical dodecagons correspond to its
inner and outer halves. The ‘Malkuth’ level of the microscopic Tree of Life, 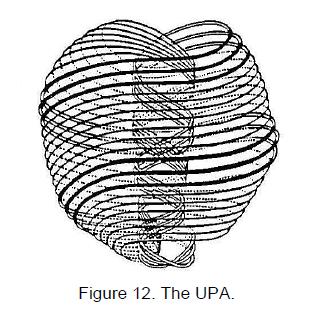 that is, each whorl of the superstring, is encoded in the tenth regular
polygon and in the last of those constituting the inner form of the Tree of Life. Each one
of the 1680 yods both shaping the pair of dodecagons and surrounding the centres of their
24 sectors denotes a circularly polarised oscillation or wave in a whorl. These yods
represent the ‘material’ manifestation of the 240 tetractyses of the 24 higher-order
tetractyses making up the pair of dodecagons. The question arises: what do these
higher-order tetractyses denote? Twenty-four of them are associated with each whorl, that
is, 240 higher-order tetractyses are associated with the UPA itself. The gauge symmetry
group E8 describing the unified superstring force has 240 so-called
‘generators’ corresponding to the 240 so-called ‘non-zero roots of its Lie algebra.’ To
each generator corresponds a kind of charge analogous to the electric charge of a
particle. Each charge is the source of a gauge field, i.e., a particular kind of force.
Each higher -order tetractys represents one of the 240 gauge charges, and 24 such charges
are spread along each whorl, making a total of (10×24=240) for the superstring itself. As
1680 = 24×70 and the Tree of Life comprises 70 yods when its 16 triangles are turned into
tetractyses (see Figure 5), this number is the number of yods in 24 separate Trees of
Life. This reflects the fact that the 24 gauge charges manifesting in each whorl are all
independent and ‘smeared’ along its length in a way analogous to that proposed in the
E8×E8 heterotic model of the superstring. 70 is also the number of
yods corresponding to Sephiroth of Construction in the higher -order tetractys making up
each sector of the dodecagons, showing again that the gauge charges are wholes —
complete Tree of Life entities in themselves. that is, each whorl of the superstring, is encoded in the tenth regular
polygon and in the last of those constituting the inner form of the Tree of Life. Each one
of the 1680 yods both shaping the pair of dodecagons and surrounding the centres of their
24 sectors denotes a circularly polarised oscillation or wave in a whorl. These yods
represent the ‘material’ manifestation of the 240 tetractyses of the 24 higher-order
tetractyses making up the pair of dodecagons. The question arises: what do these
higher-order tetractyses denote? Twenty-four of them are associated with each whorl, that
is, 240 higher-order tetractyses are associated with the UPA itself. The gauge symmetry
group E8 describing the unified superstring force has 240 so-called
‘generators’ corresponding to the 240 so-called ‘non-zero roots of its Lie algebra.’ To
each generator corresponds a kind of charge analogous to the electric charge of a
particle. Each charge is the source of a gauge field, i.e., a particular kind of force.
Each higher -order tetractys represents one of the 240 gauge charges, and 24 such charges
are spread along each whorl, making a total of (10×24=240) for the superstring itself. As
1680 = 24×70 and the Tree of Life comprises 70 yods when its 16 triangles are turned into
tetractyses (see Figure 5), this number is the number of yods in 24 separate Trees of
Life. This reflects the fact that the 24 gauge charges manifesting in each whorl are all
independent and ‘smeared’ along its length in a way analogous to that proposed in the
E8×E8 heterotic model of the superstring. 70 is also the number of
yods corresponding to Sephiroth of Construction in the higher -order tetractys making up
each sector of the dodecagons, showing again that the gauge charges are wholes —
complete Tree of Life entities in themselves.
9
The last statement should answer the following question that may have arisen
in the reader’s mind during the discussion above of how the number 1680 was embodied in the
pair of dodecagons: what, if any, is the significance of the seemingly arbitrary way in which
the 840 yods in each dodecagon were selected — namely, picking out the 840 yods that surround
centres of sectors? The yod at the centre of a tetractys denotes Malkuth, the material
manifestation of the whole symbolised by the tetractys. The six yods surrounding it at the
corners of a hexagon denote the six Sephiroth of Construction above Malkuth. There are 84 yods
surrounding the centre of the next higher -order tetractys (see Figure 9). On the cosmic level, these correspond to the 42 subplanes of the
six superphysical planes of consciousness and the 42 subplanes of their cosmic
counterpart (see Article 5 for more details). On the microcosmic level, they denote the
number of circularly polarised waves in a quarter of a revolution about the axis of the UPA,
i.e. , a 90° turn in space. In conformity with its ten-fold nature — both in ordinary space
and in 10-dimensional space-time — each whorl makes ten half-revolutions, five
in an outer twisting and five in a more tightly knit, double helical twist. This 5:5 split
corresponds to the division in the Tree of Life between the five uppermost Sephiroth, which
span its Upper Face, and the five lowest Sephirah forming its Lower Face. The yod at the
centre of a higher-order tetractys denotes the Malkuth level of manifestation of a Tree of
Life system and so does not enter the count of the yods symbolising differentiations of
Sephiroth beyond Malkuth. Each of the 24 gauge charges spread out along each
whorl is that manifestation. What appears at first sight to be merely an
ad hoc choice of yods contrived to generate the number 840 in each dodecagon is in
fact a selection dictated by the proper, physical interpretation of their
higher-order tetractys sectors.
Another similarity between the powers of the square and dodecagon to embody
various superstring parameters like 248 and 168 is
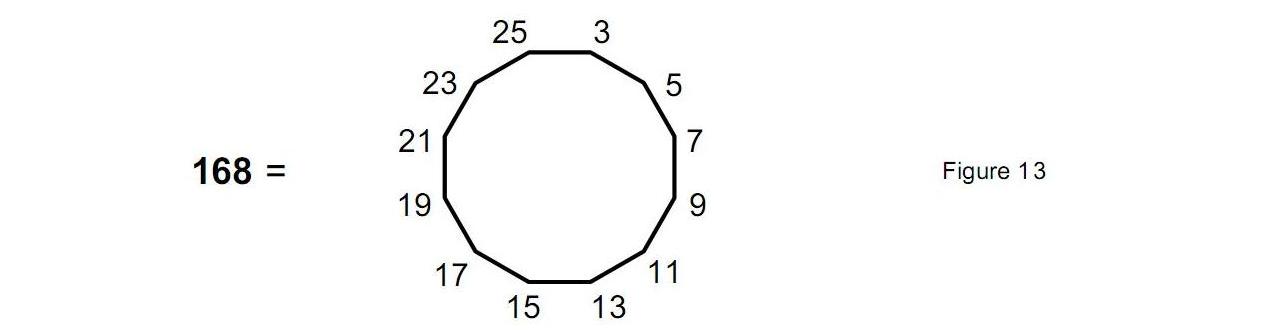
the fact that the latter number is the sum of the first 12 odd integers after 1 (Fig. 13) and that the shapes of both polygons are defined by the number 12
because a square divided into tetractyses has 12 yods along its boundary, whilst a dodecagon
is delineated by its 12 corners. As the template for constructing objects possessing sacred
geometry, the tetractys unveils a beautiful harmony between geometry and arithmetic that
exists only in such objects.
5. Encoding of 336 in
the pair of dodecagons
Two joined dodecagons have 22 corners, where
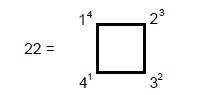
Its 24 (=1×2×3×4) sectors have 24 corners. This illustrates once more how
the integers 1, 2, 3, & 4 express properties of the dodecagon. As there are 22 compactified
dimensions in 26-dimensional space-time, each corner of a dodecagon can be
regarded as symbolising the higher dimensions of space. The ten corners outside the
root edge of one dodecagon symbolise the ten curled-up dimensions generating the ten string-
like components of the superstring (see Article 2). The twelve corners of the other dodecagon
denote the twelve remaining compactified dimensions. These consist of the five dimensions that
define a compactified space whose symmetry generates the superstring gauge group E8
and the seven curled-up dimensions predicted by supergravity theory. The centres of the two
dodecagons symbolise the two transverse dimensions of 26-dimensional
strings.
Notice that the division:
22 = 3 + 7 + 12
of the 22 letters of the Hebrew alphabet into the three mothers: aleph, mem
& shin, the seven double
10
consonants: beth, gimel, daleth, caph, pe, resh, & tau, and the twelve
simple consonants has a remarkable geometrical counterpart in the 22 corners of the pair of
joined dodecagons. This is because the three mother letters correspond to three corners
symbolising the curled-up dimensions beyond supergravity space-time that generate the three
major whorls of the UPA, the seven double consonants correspond to seven corners that denote
the curled-up dimensions generating its seven minor whorls and the twelve simple consonants
correspond to the corners of the other dodecagon that

symbolises the five E8-generating dimensions and the seven
curled-up, supergravity dimensions.
Property number 22 in the list given in Section 2 states that the number of
yods in two joined dodecagons other than their 22 corners is 336 (Fig. 14), where
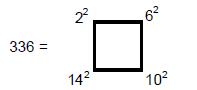
Starting with the Tetrad, 22= 4, the sum of the squares
of the four integers 2, 6, 10 & 14 spaced four units apart is 336. It was
stated in the last section that the inner and outer halves of a whorl makes 2½ revolutions.
This means that its 1680 turns are spread over five revolutions, 336 turns per revolution. Each
turn in a revolution of a whorl is symbolised by a yod in the two joined, Type B dodecagons
other than their 22 corners and two centres, that is, new yods generated by their
construction from tetractyses. The 168 such yods in each
dodecagon denote the number of circularly
polarised oscillations made during the traverse of either half of one
revolution of a whorl.
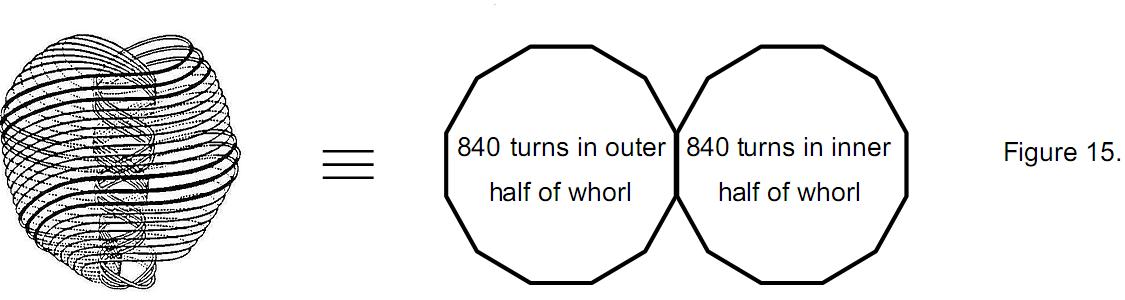
With their sectors turned into the next higher-order tetractys after the
Pythagorean tetractys, each dodecagon was found earlier to contain 840 yods outside their root
edge surrounding their centres. Each dodecagon represents half of a whorl made up of 840 coils
(Fig. 15). Enfolded in each Tree of Life belonging to CTOL are the two sets
of seven regular polygons. The lowest ten Trees of Life have 140 enfolded
polygons, where 140 is the number value of Masloth, the Mundane
Chakra of Chokmah. Their 20 dodecagons contain (10×1680=16,800) yods outside their root
edges surrounding the centres of their 240 sectors representing the 240 gauge charges of
E8. This Tree of Life representation of the superstring shows that the Godname
ADONAI prescribes the number 16,800 because its number value 65 is the
number of SLs in the lowest ten trees of CTOL. The number of corners of the 70 polygons
enfolded on either side of these trees is 351, which is the number value of
Ashim, the Order of Angels assigned to Malkuth. 351 is also the
sum of the first 26 integers, showing how the Godname YAHWEH with number
value 26 prescribes the ten overlapping Trees of Life representing the ten
whorls of the superstring. Each dodecagon has ten
11
corners outside its root edge. The ten dodecagons enfolded in the lowest ten
trees have (10×10=100) external corners. This means that the 60 polygons enfolded on either
side of the ten trees that are not dodecagons have (351–100=251) corners.
Article 5 (6) discussed the significance of the number 251 in relation to the
superstring. The concurrence in the same context (the lowest ten trees) of
this structural parameter encoded in the first six types of polygons with the number 16,800
encoded in the seventh type is remarkable evidence for the Kabbalistic basis of superstring
theory and the author’s identification of the UPA as a superstring. Notice that the
proportion of the dodecagons to the first six types enfolded in ten trees, namely, 10:60,
corresponds in the tetractys-transformed Tree of Life to the 10:60 pattern of yods created
by the ten Sephiroth and the 60 hexagonal yods. Indeed, the inner form of the Tree of Life
has the same pattern, namely, the ten corners of a dodecagon outside the root
edge that it shares with the other 13 polygons with 60 corners. Just as the points in space
where the ten Sephiroth are located define the basic geometrical aspect of the Tree of Life
— its Malkuth level — so their counterpart in its inner form — the pair of dodecagons —
quantitatively embodies the physical nature of the Tree of Life in the subatomic world as
measured by the 1680 coils in each helical whorl that makes up the UPA/superstring. One can
only affirm the hermetic axiom: “as above, so below.”
6. Encoding of 248
& 168 in Type A & Type B dodecagons
Up till now, both dodecagons have been regarded as the same type. Suppose that one of the
dodecagons is Type A and that the other is Type B. The former contains
73 yods and the latter has 181 yods. The pair of joined dodecagons has
250 yods. We saw above that the first six types of polygons enfolded in ten overlapping trees
of Life have 251 corners. The topmost corner of the hexagon enfolded in the tenth tree
coincides with the lowest corner of the hexagon enfolded in the 11th tree. 250 corners are
therefore intrinsic to these polygons. They correspond to the 250 yods in a Type A and Type B
dodecagon, thereby further demonstrating the holistic nature of the pair of dodecagons. As
Articles 5 and 6 discuss in more detail, the UPA is formed from a d-brane embedded in
26-dimensional space-time that wraps itself around ten circular dimensions to
generate the ten independent whorls of the superstring. A point on each whorl is specified by
25 spatial coordinates, so that the ten whorls have (10×25=250) such variables.
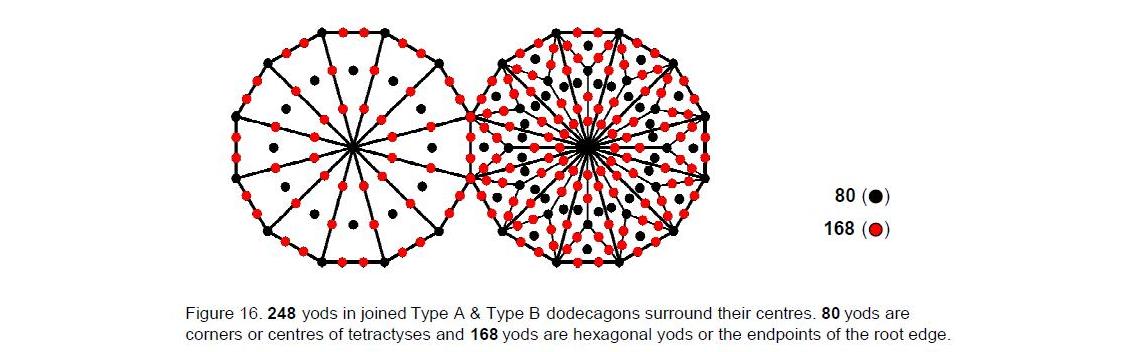
We see that the two types of dodecagon embody the number of variables defining the positions of
ten points in 26-dimensional space-time which can never coincide, i.e., they
belong to ten curves that never touch or intersect. This is highly significant, for it is
evidence for the ten-fold nature of the superstring. 248 yods surround
the centres of the joined dodecagons, where 248 is the number value of
Raziel, the Archangel of Chokmah (Fig. 16). They symbolise the 248 gauge bosons of
E8 that transmit the unified superstring force.
246 yods are outside the root edge, where 246 is
the number value of Gabriel, the Archangel of Yesod. According to the properties
listed on pages 3 and 4, the Type A dodecagon has 49 geometrical
elements, where 49 is the number of EL ChAI, Godname of Yesod, and the
Type B dodecagon has 121 geometrical elements. The pair of separate dodecagons has 170
geometrical elements, i.e., they have 168 geometrical elements
surrounding their centres. In other words, 168 geometrical
elements are needed to construct their 48 tetractyses, starting from their two
centres. The pair of joined dodecagons embodies the superstring dynamical
parameter 248 because 248 yods are needed to
construct them, starting from their two centres, and the pair of separate dodecagons
embodies its structural parameter 168 because
168 geometrical elements are needed, as well as
168 yods, starting from a dodecagon divided into its sectors. This is
more remarkable evidence of how the Malkuth aspect of the microscopic manifestation of the
Tree of Life is encoded in the last of the regular polygons constituting its inner form.
48 is the number value of Kokab, the Mundane
12
13
Chakra of Hod, the Sephirah that signifies mental activity and
communication. Previous articles discussed how this number is a parameter of the Tree of Life,
being the number of corners of the seven separate, regular polygons making up its inner form
and the number of corners, edges & triangles making up its outer form. Its superstring
interpretation is as follows: as discussed earlier, each of the 24 gauge charges carried by a
string component of the superstring/UPA manifests as a circularly polarised standing wave. Each
such wave has two orthogonal, plane wave components that are 90º out of phase. Each whorl
therefore consists of (2×24=48) independent standing plane waves. This 24:24
division manifests geometrically in the Type A dodecagon as the 24 vertices & edges on its
boundary and the 24 edges and triangles inside it. The pattern appears in the first (6+6)
enfolded polygons as the 24 corners intrinsic to each set. As future articles will demonstrate,
it is a characteristic of any holistic system possessing sacred geometry. The ten
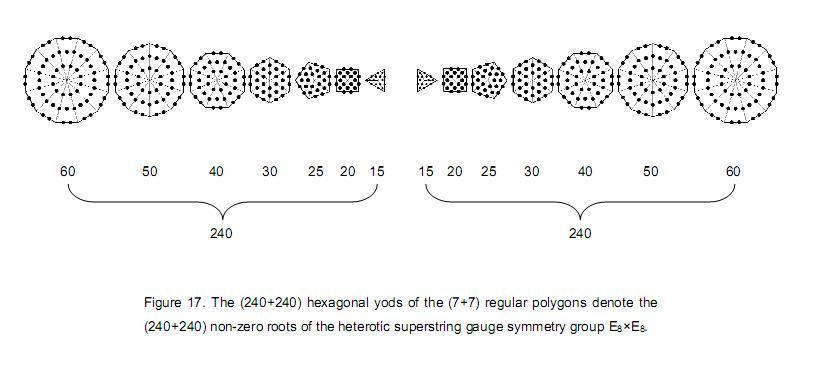
whorls of the UPA/superstring comprise (10×48=480) plane waves. The encoding
of these in the inner form of the Tree of Life is the set of 240 hexagonal yods in either set
of seven separate regular polygons, i.e., their 480 hexagonal yods (Fig. 17). In the case of the first (6+6) enfolded polygons enfolded in ten
Trees of Life, the two sets of 240 plane waves are the counterpart of the (240+240) corners
of the (60+60) polygons of the first six types. Every hexagonal yod or corner in one set is
the mirror image of its counterpart in the other set. Every such pair denotes the two
orthogonal plane waves making up each of the 24 circularly polarised oscillations in each of
the ten whorls of the superstring constituent of up and down
quarks paranormally described over a century ago by the Theosophists Annie
Besant and C.W. Leadbeater.
The numbers of corners, edges & triangles surrounding the centres of the
separate Type A and Type B dodecagons are:
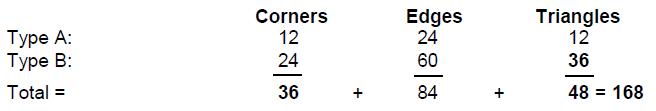
There are 84 edges and 84 corners & triangles. This 84:84 division of
the 168 geometrical elements in the two types of dodecagons is characteristic
of holistic systems. Later articles will provide numerous examples. Its remarkable consequence
is that, if we consider the ten dodecagons enfolded on one side of the central pillar of ten
overlapping Trees of Life as Type A and their counterparts on the other side as Type B, the ten
pairs of separate dodecagons have 840 edges and 840 corners and triangles. This is the
same 840:840 division as was found for the yods surrounding the centres of the 24
sectors of two enfolded polygons when each sector is a higher-order tetractys. It manifests
physically as the 840 circularly polarised waves in each half of a whorl of the
E8×E8 heterotic superstring. Here is clear evidence that the
superstring’s oscillatory form, as described by Besant & Leadbeater, conforms to the
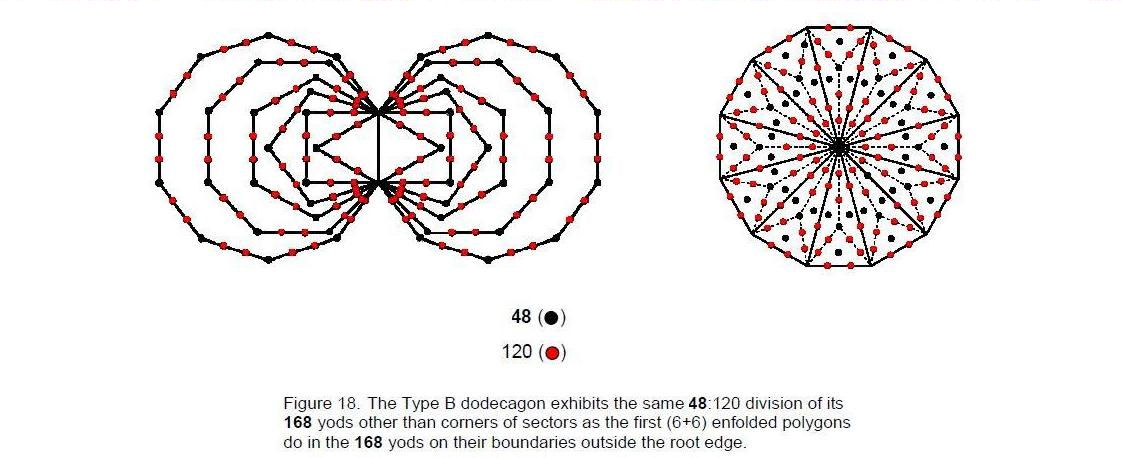
geometry of the pair of dodecagons in the inner Tree of Life. The Type A dodecagon has
48 elements surrounding its centre and the Type B has 120 elements surrounding
its centre. The counterpart of this 48:120 division in a Type B dodecagon with
168 yods other than the 13 corners of its 12 sectors is the
48 yods at corners & centres of tetractyses and the 120 hexagonal yods on
their 60 edges (Fig. 18). Its counterpart in the 168 yods outside
14
the root edge on the sides of the first (6+6) enfolded polygons is their
48 corners and the 120 hexagonal yods on their 60 sides. Equivalent holistic
structures always display analogous patterns.
7.
Conclusion
The dodecagon and the pair of joined dodecagons in the inner form of the Tree of Life can be
transformed into two types, depending on whether their sectors are turned into single
tetractyses or three tetractyses. The ten Godname numbers prescribes their resulting
properties, suggesting that they embody numbers of cosmic significance. This is confirmed by
the way they encode the numbers 168 and 336, these being the number of
coils in, respectively, half and one revolution of a string component of the superstring
constituent of up and down quarks, proved by the author to have described paranormally with a
yogic siddhi over a hundred years ago by the two Theosophists Annie Besant and C.W. Leadbeater.
A pair of dodecagons is found to embody the number (1680) of such coils in all five revolutions
of a string when their sectors are constructed from the next higher-order tetractys. As each of
the ten strings of the superstring is the space- time manifestation of a Sephirah, it, too, can
be represented by a Tree of Life. This means that the superstring is modelled by ten
overlapping trees in whose inner forms are enfolded 20 dodecagons containing 16,800 yods that
are outside their root edges and surround the centres of their 240 sectors. These correspond to
the 16,800 coils in the superstring. They denote circularly polarised oscillations in its ten
strings generated by the 240 gauge charges of the superstring symmetry group E8,
which are ‘smeared’ along each whorl, 24 per whorl. These gauge charges are the physical
meaning of the 24 higher-order tetractys sectors in the pair of dodecagons enfolded in each
overlapping Tree of Life as the last of the regular polygons constituting its inner form. A
Type A dodecagon and a Type B dodecagon separately have 168 geometrical
elements surrounding their centres, whilst, joined together, they have
248 yods unshared with the outer form of the Tree of Life or,
alternatively, 248 yods surrounding their centres. These yods symbolise
the 248 gauge bosons of E8. Superstring physics has been
reduced to sacred geometry and then to number as its generating principle. Truly, as the
Pythagoreans declared: “Number is form and form is number.”
References
1. Phillips,
Stephen M. Article 9: “How the square encodes the superstring parameters 168 & 248,”
(WEB, PDF), pp. 2–9.
2. Phillips, Stephen M. Article 1: “The Pythagorean nature of superstring
and bosonic string theories,” (WEB, PDF), p. 4.
3. The number of yods in a polygon with n corners is: N = 6n + 1 (Type A); N
= 15n + 1 (Type B). A Type A dodecagon (n=12) has
73 yods. A Type B dodecagon has 181 yods.
4. Formulae for a polygon with n corners:
|
|
Type A
|
Type B
|
|
Number of hexagonal yods in polygon with n corners =
Number of corners of triangles =
Number of sides of triangles =
Number of triangles =
Number of corners & sides =
Number of corners & triangles =
Number of sides & triangles =
Number of corners, sides & triangles =
|
5n
n + 1
2n
n
3n + 1
2n + 1
3n
4n + 1
|
13n
2n + 1
5n
3n
7n + 1
5n + 1
8n
10n + 1
|
5. Ref. 1.
6. Phillips, Stephen M. Article 5: “The superstring as microcosm of the spiritual
macrocosm,” WEB, PDF).
15
|