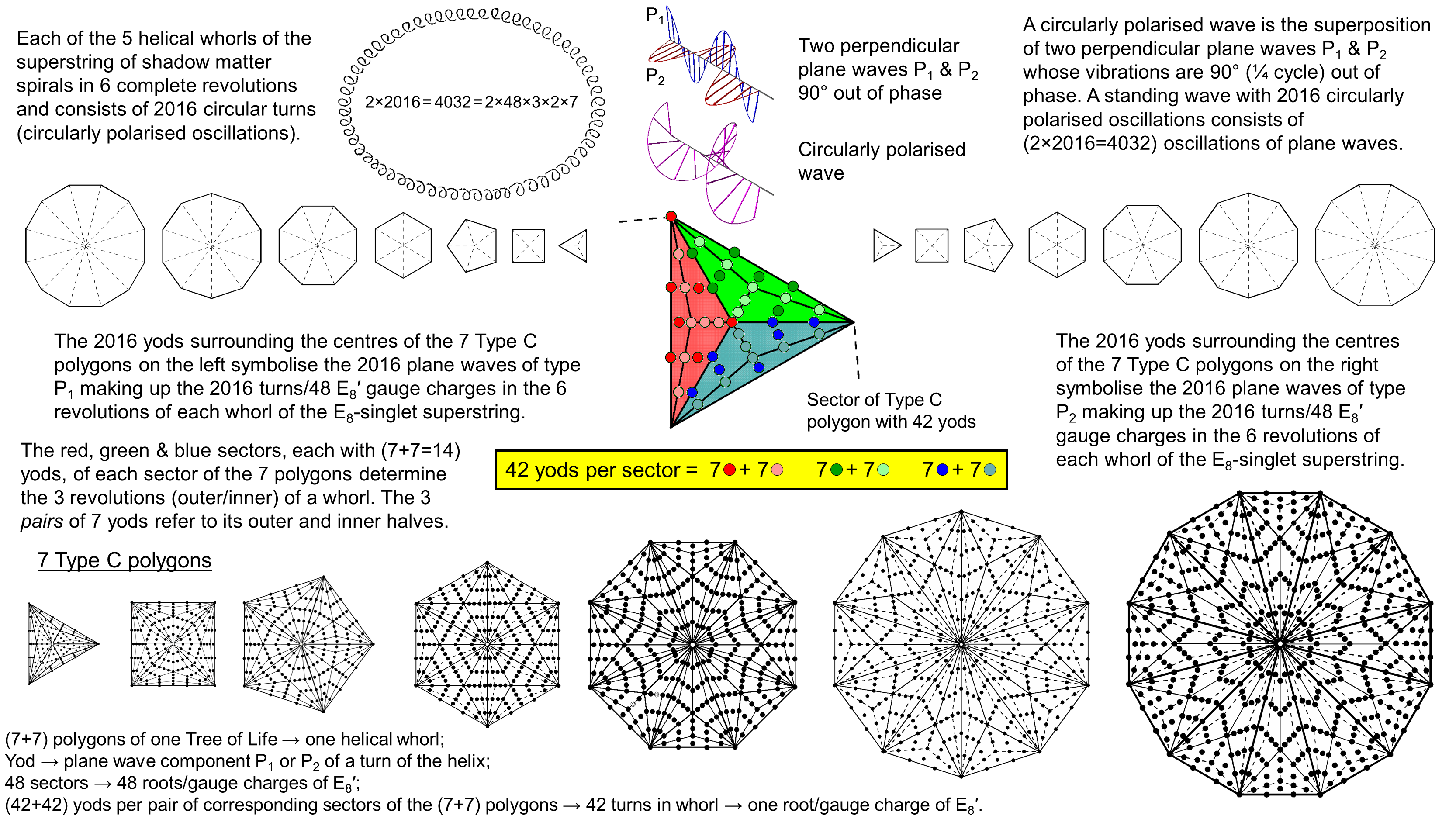
The (2016+2016) yods in the (7+7) separate Type C polygons of the inner Tree of Life denote the (2016+2016) plane
waves that form the 2016 circularly polarised oscillations in each whorl of the basic particle of shadow matter.
| << Previous 1 2 [3] 4 5 ...24 Next >> |
#3 The Tree of Life basis of the fundamental particle of shadow matter
We have just seen that the structural parameter 2016 of the basic particle making up the human vital body (the yogic "pranamaya kosha"), as inferred from Ron Cowen's micro-psi observations, is embodied in the inner form of the four Trees of Life that are uppermost in the 7-tree mapping the seven subplanes of the physical plane. Given that the factor of 4 in this number does not play a role in its reported form and therefore cannot be alternatively attributed to its structure in some way, its presence is apt because the number of etheric subplanes, whose forms of matter are aggregates of this particle, is four. If it had been, say, three or five, the number 2016 could not have arisen in the intrinsic yod population of the inner form of this number of Trees of Life. That it should contain the factor of 4, which (as emphasised above) cannot arise from the morphology of the particle (five whorls, not four; six revolutions of each whorl, not four), is very significant, for it is evidence that Cowen's particle is, indeed, the basic unit of the matter of the human vital body that functions solely on these four subplanes. Another indication of this is as follows: the 49-tree and the 7-tree map, respectively, the cosmic physical plane and the physical plane (Theosophy distinguishes the latter from the former by calling it the "solar physical plane"). As expressions of the same Sephirah, namely, Malkuth, these sections of CTOL bear a metaphysical correspondence to each other. In the same way, the uppermost four etheric subplanes of the solar physical plane have a correspondence with the uppermost four planes of the cosmic physical plane, whose 28 subplanes are mapped by 28 Trees of Life. As 2016 = 28×72, where 72 is the number of yods surrounding the centre of the Type A dodecagon, those 28 Trees in the 49-tree that are analogous to the four uppermost Trees in the 7-tree have an inner form whose 28 dodecagons have 2016 yods surrounding their centres. What this is indicating is that the Malkuth (tenth Sephirah) aspect, expressed by the dodecagons — the tenth type of regular polygon, of the higher counterpart to the four etheric subplanes embodies the structural parameter 2016 of the basic constituent of shadow matter existing on these subplanes. This is no coincidence! It is an unambiguous illustration of the well-known Hermetic principle: "As above, so below." Analogous domains of CTOL embody the same parameters quantifying their properties.
Let us now suppose that the seven types of regular polygons making up the inner Tree of Life are
Type C (they are discussed in Article 60). This means that their sectors are Type B triangles containing 46 yods,
i.e., there are 42 yods per sector. As the seven polygons have 48 sectors, the total
number of yods surrounding their centres = 48×42 = 2016. It might be thought that each yod
symbolises one of the 2016 turns in each helical whorl of the basic particle of shadow matter, namely, the
E8-singlet sector of E8×E8′ heterotic superstrings. But things are somewhat
more subtle. Each circular turn of a whorl is a circularly polarised wave formed by the superposition of two
plane waves oscillating in directions at right angles to each other 90° (¼ cycle) out of phase. They are
coloured blue (P1) and brown (P2) in the diagram below:
 |
|
Without specifying what precisely is vibrating here (whether it is a string, D-brane, etc), the whorl is a circularly polarised wave made up of (2×2016=4032) plane wave oscillations, that is, 2016 pairs of perpendicular, sinusoidal oscillations that differ in phase by 90°. The complete, inner form of the Tree of Life comprises two sets of 7 regular polygons, those in one set being the mirror image of those in the other set. Every one of the 2016 yods in one set has its mirror image counterpart in the other set. A yod and its mirror image symbolise the pairing of plane waves to form a circularly polarised wave of constant amplitude whose direction rotates 2016 times in full circles as it travels six times around the axis (of spin?) of the particle, making 336 oscillations in each cycle of revolution. Each of the 48 sectors of the seven polygons signifies a root or gauge charge of E8′ (we are ignoring its symmetry breaking at this stage). To be more accurate, a sector and its mirror image in the second set of polygons denote that because we are interpretating the two halves of the inner Tree not as the physical halves of a helical whorl but as their vibratory halves, being composed of 2016 P1 plane waves symbolised by yods in one set of seven polygons and 2016 P2 waves denoted by yods in the set of their mirror images. This means that a sector and its mirror age counterpart contribute 84 yods that denote the 42 circular turns (84 plane waves) carrying one E8′ gauge charge. Each Type B-triangular sector consists of three Type A triangles, coloured red, green & blue. Each triangle has 14 yods that form two sets of seven (dark & light shades of these colours). This three-fold division of a sector expresses the fact that a whorl revolves three times in an outer spiral and three times in a tighter, inner spiral. Each set of seven polygons is made of two "halves": the triangle, square, pentagon & dodecagon with 24 sectors and the hexagon, octagon & decagon with 24 sectors (for a complete discussion of their properties, see Article 64). The number 48 is a structural parameter of sacred geometries, and its 24:24 division is characteristic of them (see The holistic pattern). One set of 24 sectors corresponds to the 24 E8′ gauge charges spread along the outer half of a whorl and the other set of 24 sectors corresponds to the 24 charges spread along its inner half (we say "correspond" with the qualification that the correspondence actually involves a set of polygons with 24 sectors and its mirror-image counterpart in the other set of seven polygons).
We found earlier that the tenth overtone with tone ratio 24 is at the centre of a Lambda Tetractys, the sum of whose nine surrounding numbers = 14×24 = 336, which is the number of circular turns per revolution of a whorl — whether it belongs to the UPA or to the basic particle of shadow matter. As 144 = 6×24 and the latter has whorls that make six revolutions, the number 2016 is the sum of the nine musical number weights that surround the number weight 144:
|
24 |
|||
|
48 |
72 | ||
|
96 |
144 |
216 |
|
|
192 |
288 |
432 | 648 |
Amazingly, the note with this number as its tone ratio (the major second of the eighth octave) is the 22nd overtone. In other words, if the first 10 overtones are assigned to the 10 Paths that make up the trunk of the Tree of Life and the next 12 overtones are assigned to the 12 Paths that make up its branches, the last overtone assigned to Paths in the trunk generates the superstring structural parameter 336 common to E8-singlet and E8′-singlet states of E8×E8′ heterotic superstrings, whereas the last overtone assigned to Paths in the branches generates the number of turns in a whorl of the former: 2016 = 6×336. There is no musical association for the helical whorl of the UPA with 1680 turns because 1680 = 14×120, and there is no musical number weight that has a magnitude of 120. However, this number appears in the inner Tree of Life as the number of yods lining the sides of its seven polygons, inside which are 144 yods. Once again, the distinction between boundaries and interiors generates the ratio 144/120 = 6/5. The whorls of the two basic particles exhibit the same proportion because 2016/1680 = 144/120 = 6/5. Their polyhedral counterparts in the Polyhedral Tree of Life are the 144 Polyhedron with 72 vertices surrounding its axis and the disdyakis triacontahedron with 60 vertices surrounding its axis, where 72/60 = 6/5 (see page 1 of this section and also Polyhedral Tree of Life).
The seven Type C polygons express the oscillatory form of each whorl of the shadow matter superstring (no doubt that this is actually only its ground state). As the 240 roots/gauge charges of E8′ are spread along the five oscillating whorls, 48 charges per whorl, one would expect this 5×48 pattern to be reflected in the distribution of yods in the polygons. Indeed, we do see this. There are per sector of the Type C polygon one external corner and four internal corners, i.e., five corners, so that the seven separate Type C polygons have (5×48=240) corners. They symbolise the 240 roots of E8′. But what about the second set of seven polygons that are the mirror images of the counterpart in the first set? The basic particle of shadow matter is the E8-singlet state of the E8×E8′ heterotic superstring and therefore it does not carry the charges of E8. We have just seen that the (7+7) separate Type C polygons express the plane waves making up the circularly polarised oscillations of its whorl. But we are at liberty to interpret the inner form of the Tree of Life in several different contexts simultaneously, for it is the universal blueprint that encodes both the form and the dynamics of
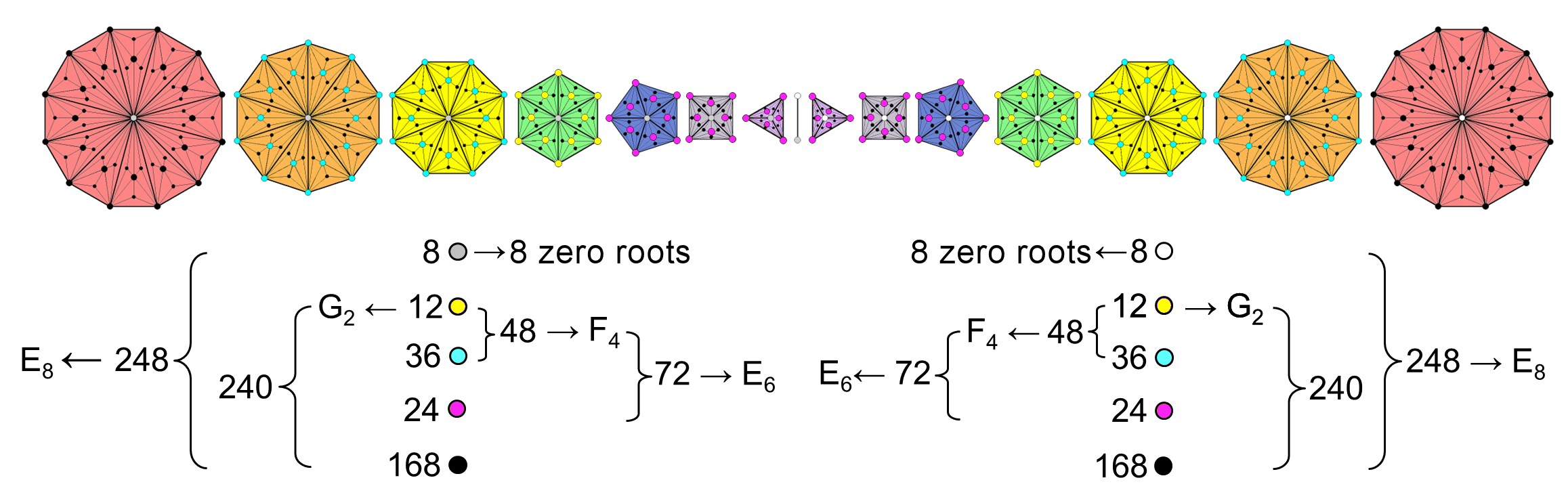 |
|
fundamental particles. This means that the 240 corners of the (9×48=432) triangles in one set of seven Type C polygons that surround their centres denote the 240 non-zero roots of E8 and that the 240 corners in the second set denote the 240 non-zero roots of E8′. The seven zero (or so-called "simple") roots of E7 (the largest exceptional subgroup of E8) are denoted by the centres of the seven polygons; the remaining simple root of E8 is denoted by an endpoint of the root edge that can be added to separate the two sets of polygons; similarly for E8′. Far from being a mere, mathematical contrivance to make numbers tally, there is precedence for adding the root edge when considering the polygons as separate, for it is encountered in the encoding of CTOL in the inner Tree of Life (see here), where the four yods in the root edge separating two sets of polygons denote the four highest SLs in the 49-tree that maps the cosmic physical plane. The 48 sets of five types of corners symbolising roots of E8′ can be, alternatively, regarded as five sets of 48 corresponding types of corners. This is consistent with Cowen's description of the basic particle of the vital body as having five whorls, and it supports the idea that each whorl carries 48 gauge charges of E8′. Although he never counted the number of turns in a helical whorl, nor checked (as Leadbeater did for the UPA) that different whorls contain the same number of turns, this is what the five-fold pattern of corners in every one of the 48 sectors of the seven polygons is indicating.
When the factorisation 2016 = 48×42 = 48×7×6 is rewritten as 7×48×6 = 7×288, it enables us to establish a connection between the seven subplanes of the physical plane, as mapped by the 7-tree, and the inner form of each Tree of Life as sets of seven regular polygons that have 288 yods surrounding their centres when they are separate and Type A. The number 288 has a Pythagorean significance. Suppose one arranges 10 different objects in a tetractys array. How many arrays can be created by re-arranging the objects within each of its four rows? There is 1! (=1) way of arranging the single object in the first row, 2! (=2) ways of permuting the two objects in the second row, 3! (=6) ways of permuting the three objects in the third row and 4! (=24) ways of re-arranging the four objects in the last row. Re-arranging all rows generates 1!×2!×3!×4! = 1×2×6×24 = 288 different tetractyses, each made up of the same 10 objects. Each tetractys contains seven objects located at the centre and corners of a hexagon. The number 2016 is the number of objects in these 288 different tetractyses that occupy the positions of the seven hexagonal yods symbolising the seven
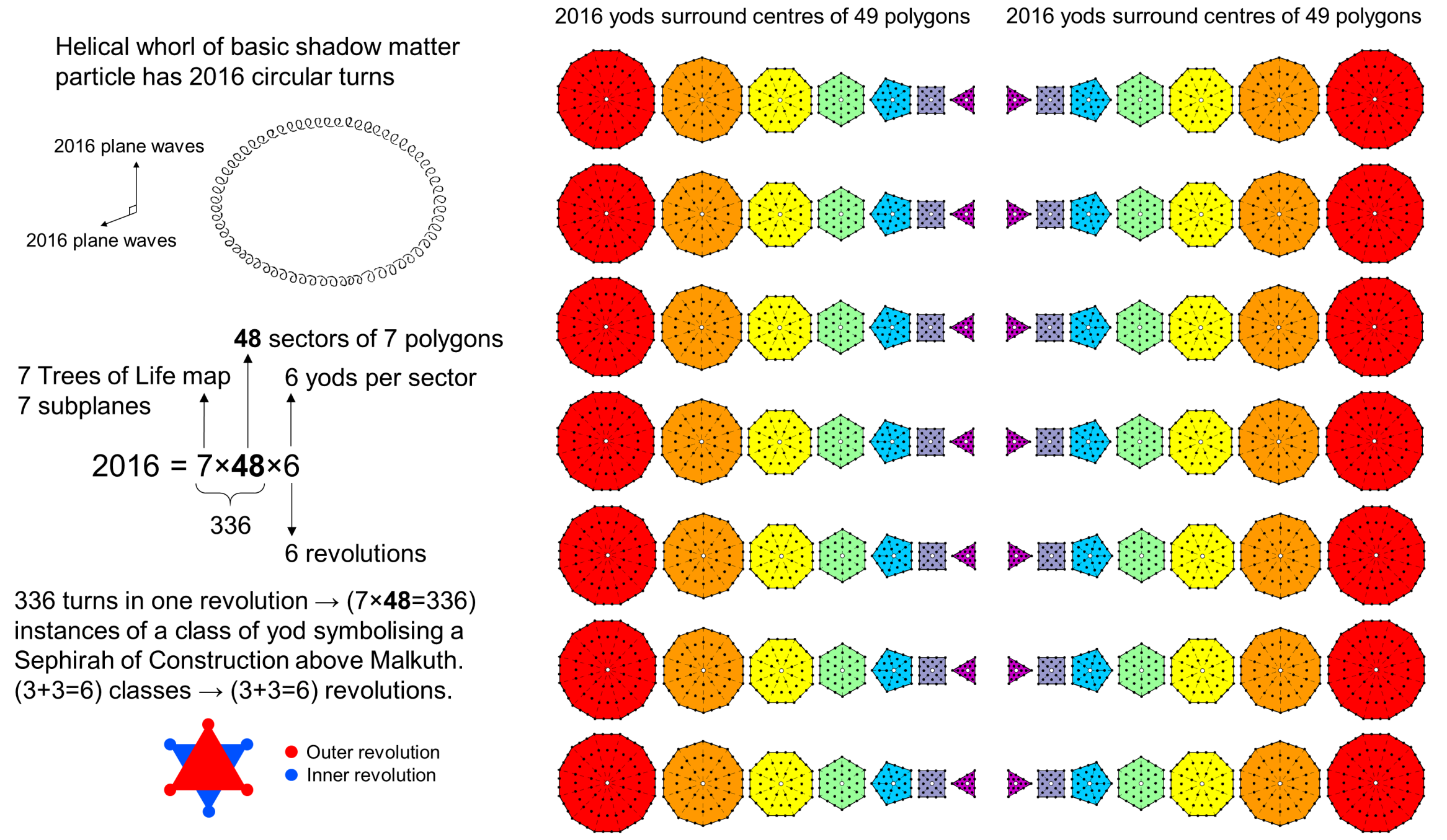 |
|
Sephiroth of Construction. Notice that this factorisation of the number 288 is what results from dividing up the seven polygons into its two halves: the triangles, square, pentagon & dodecagon with 24 corners and the hexagon, octagon & decagon with 24 corners, each sector having six yods: 288 = 2×24×6. There is an alternative perspective. There are 144 yods inside the boundary of each set of seven enfolded polygons, which are lined by 120 yods, so that (7×288=2016) yods are inside the 2×49 enfolded polygons of the inner form of the 7-tree. In the case of separate polygons, the product 7×48 = 336 expresses that the 49 Type A polygons in the inner form of seven separate Trees of Life have 336 sectors. There are 6 yods per sector, whilst each helical whorl of the shadow matter particle makes six revolutions, each having 336 turns. One can view this structure as 336 repetitions of each class of yod symbolising one of the six Sephiroth of Construction above Malkuth. In other words, the six revolutions divided into three outer and three inner ones are expressing in turn these six Sephiroth of Construction as the two triads: Chesed-Geburah-Tiphareth and Netzach-Hod-Yesod. As in the case of Type C polygons discussed earlier, where the inner form of a single Tree of Life represents a whorl, the two sets of 49 Type A polygons, each set with 2016 yods surrounding their centres, represent the two sets of 2016 plane waves 90° out of phase whose addition generates 2016 circularly polarised waves running around each whorl. Both Type A and Type C polygons are able to represent the oscillations of each whorl of the basic particle of shadow matter because their respective numbers of yods per sector are 6 and 42 (=7×6), which means seven times as many Type A polygons have the same numbers of yods surrounding their centres as a given number of Type C polygons. Information embodied in higher-order polygons is not necessarily different to that encoded in lower-order polygons. It pertains to the same realisation of the archetypal pattern, but it is more densely 'packed,' so to speak.
The number 528 is sacred in certain ancient cultures. As 2×264, where 264 is the number of yods in the seven enfolded Type A polygons making up half of the inner Tree of Life, this number is the sum of the numbers 288 and 240, where 240 (= 2×120) is the number of yods lining the perimeter of both separate sets of seven enfolded polygons and 288 (= 2×144) is the number of yods within their boundaries. The number of oscillations in each whorl of the basic shadow matter superstring = 2016 = 7×288, whilst the number of oscillations in each whorl of the subquark state of the E8×E8′ superstring = 1680 = 7×240. The number 528 is special because it is the number of yods in the two separate, mirror-image halves of the inner Tree of Life (note: separate, not combined, for which the number is 524). Multiplied by the number 7, which is equally sacred in many cultures, the number 528 measures the total number of circularly polarised oscillations in the whorls of the basic particles of the two fundamental kinds of physical matter: the E8-singlet state and the E8′-singlet state of the E8×E8′ heterotic superstring:
7×528 = 7(288+240) = 2016 + 1680.
The geometrical meaning of this is that, when the two halves of the inner form of each Tree making up the 7-tree mapping the physical plane are separated, their 2016 internal yods symbolise the 2016 circularly polarised oscillations in each whorl of the basic shadow matter particle described by Ron Cowen and their 1680 boundary yods symbolise the 1680 circularly polarised oscillations in each whorl of the basic particle of ordinary matter that was described by Besant & Leadbeater. The structural parameters 2016 and 1680 (or, for the whole particle, 10080 and 16800) are predicted to appear in the correct, unified theory of particles and their forces that many physicists currently seek. The value of sacred geometry is that it can make predictions that can be tested. Superstring theory has often been criticised for its inability to do this. But this has resulted partly from its current, inadequate formulation on a background space-time that is treated in terms of classical (Einsteinian) physics. Sacred geometry explains why magic numbers like 496 appear in its theoretical predictions and provides clues to what dynamical parameters should arise in its properly quantised version. When so many different contexts generate the same parameters, it seems perverse to ignore them simply because of an ideological objection to the very notion of "sacred geometry" that leaves one in a state of cognitive dissonance that rejects evidence whenever it contradicts what one wants to believe.
The number of geometrical elements that surround the centre of the Type C n-gon ≡ G(n) = 28n. There are 5 corners, 14 sides & 9 triangles per sector. Surrounding the centre of the Type C dodecagon (n=12) are 336 geometrical elements (168 corners & triangles, 168 sides). As was established earlier, this number is the structural parameter of the whorls in both the UPA and the particle of shadow matter, being the number of turns in one revolution of either type of whorl. In fact, if we remember that each half of the inner form of the Tree of Life contains a dodecagon, then the true correspondence is not between 336 geometrical elements and 336 circularly polarised waves but between the 672 geometrical elements in both dodecagons and their 672 plane wave components:
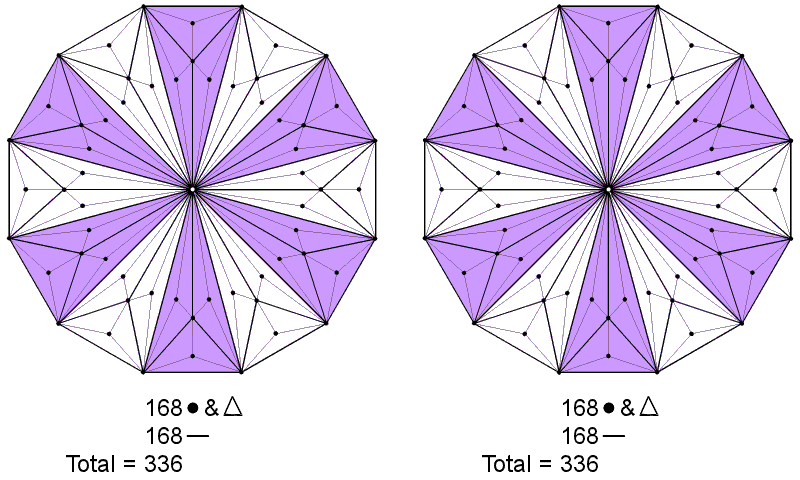 |
 |
 |
|
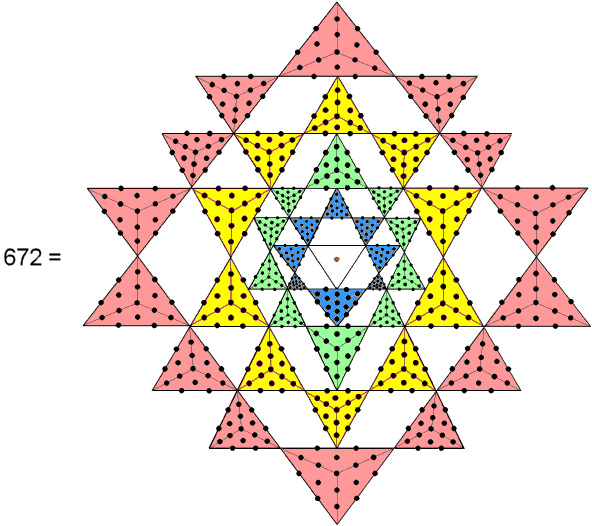
The (336+336=672) geometrical elements surrounding the centres of the two Type C dodecagons that belong to the inner form of the Tree of Life correspond to the 336 pairs of plane waves in one revolution of a whorl of both the E8-singlet and E8′-singlet states of the E8×E8′ heterotic superstring. |
When they are Type A triangles, the 42 triangles that surround the central triangle of the Sri Yantra have 672 yods other than their corners. |
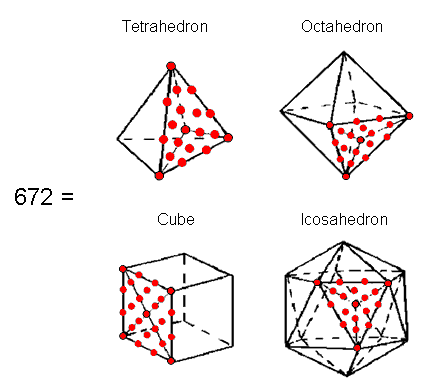
When their faces and internal triangles are Type A polygons, the first four Platonic solids have 672 yods surrounding their centres. |
The same 336:336 division is displayed by the (7+7) separate Type B polygons of the inner Tree of Life:
|
|
|
Each revolution of a whorl of an E8-singlet or E8′-singlet state of the E8×E8′ heterotic superstring conforms to the inner Tree of Life. |
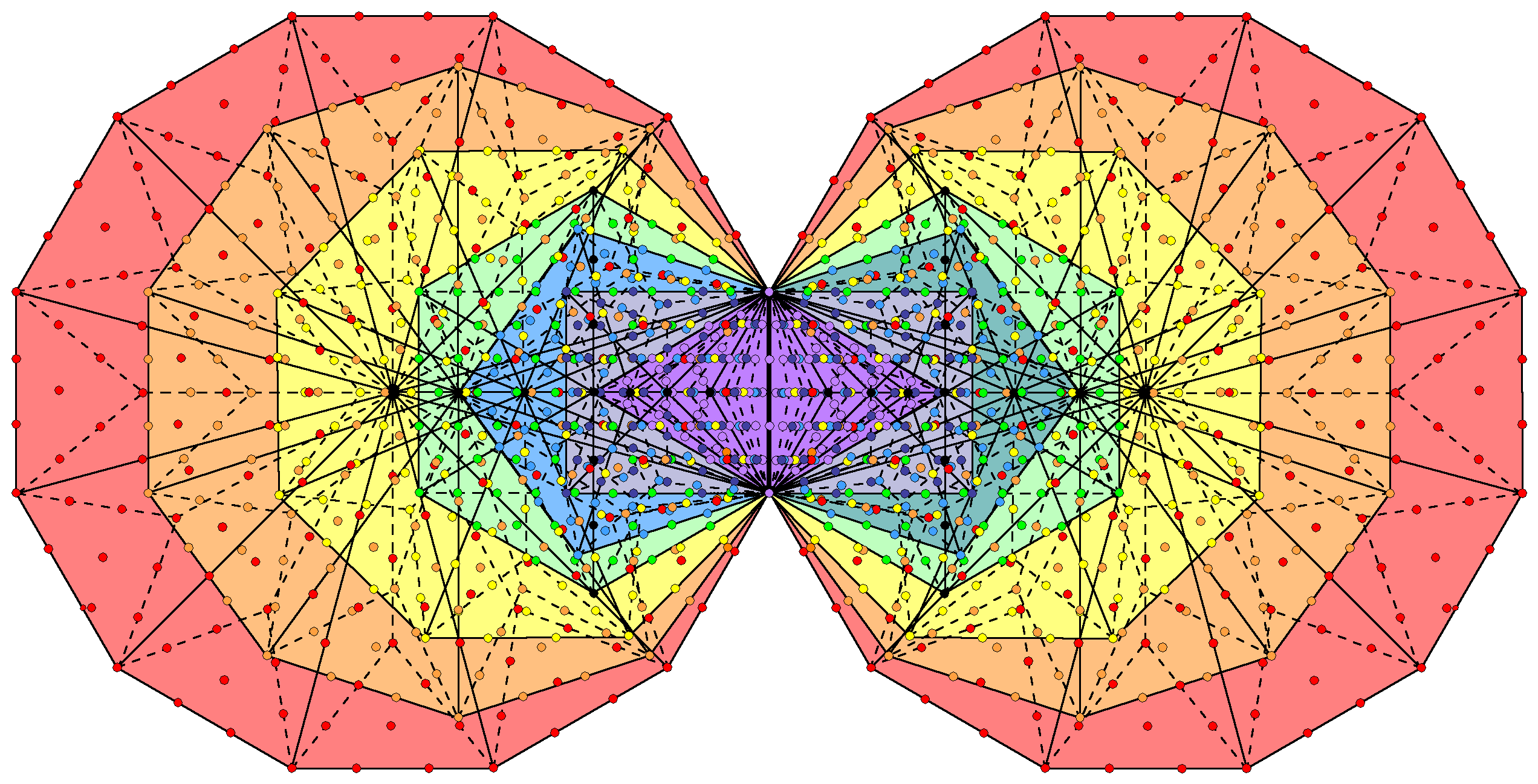
as well as by the Sri Yantra when the 42 triangles surrounding its central one are Type A triangles. Each triangle has 19 yods, i.e., 16 yods other than its corners, so that there are (42×16=672) yods other than corners of the 42 triangles. Each half of the Sri Yantra has 336 yods, there being 336 pairs of corresponding yods in its two halves that symbolise the 336 pairs of plane waves that create one revolution of a whorl of the superstring. This division is also shown by the first four Platonic solids: the tetrahedron, octahedron, cube & icosahedron that, for the ancient Greeks, were the shapes of the particles of the four physical Elements Fire, Air, Earth & Water. When their 38 faces and their internal triangles formed by joining their vertices to their centres are Type A polygons, they have 672 yods surrounding their centres, 336 yods being in each set of halves (see here). This is how these Platonic solids do shape the fundamental particles of physical matter, namely, the oscillatory shape of the E8×E8′ heterotic superstring — or at least those states that make up ordinary matter and shadow matter (their excited states are another matter). The superstring structural parameters 336 & 672 are parameters of all sacred geometries because the latter are different versions of the universal blueprint governing holistic systems. In the case of the inner Tree of Life, the number 672 is a parameter of not only the seven separate Type B polygons but also the seven enfolded Type B polygons, as now explained. There are 1370 yods in the (7+7) enfolded polygons of the inner Tree of Life when they are Type B:
 |
|
Associated with each set of 7 enfolded Type B polygons are 672 yods that are intrinsic to the inner Tree of Life and surround their centres. The 26 black yods are either centres of polygons or yods shared with the outer Tree of Life, which, for the sake of clarity, is not shown. |
Yods belonging to a polygon have the colour assigned to it. The centres of the 14 polygons are coloured black, as are the seven yods lining the two vertical sides of sectors that join the centre of each hexagon to its uppermost and lowest corners. These yods line sides of triangles belonging to the outer Tree of Life (not shown), as do the centres of the two enfolded triangles of the inner Tree of Life, which coincide with the pair of hexagonal yods lining the base of the triangle with Tiphareth, Netzach & Hod at its corners. This means that there are (14+6+6=26) black yods that are either centres of polygons or shared with the outer Tree. The number of yods that are intrinsic to the inner Tree of Life and surround centres = 1370 − 26 = 1344. Associated with each half of the inner Tree of Life are (1344/2=672) yods which, because they are intrinsic to the inner Tree of Life and surround centres, shaping the polygons, determine the form of the inner Tree of Life. This reveals the structural character of this number. The inner Tree of Life contains 672 pairs of yods that are mirror images of each other. If we consider the inner form of 10 overlapping Trees of Life, the 140 polygons making up their inner forms have 6720 pairs of such yods. As there are 24 black yods per set of 14 polygons, there are 240 yods shared with the 10 Trees of Life, making a total of 13680 yods. Compare this with the 421 polytope to be discussed shortly. This is the 8-d polytope whose 240 vertices represent the 240 roots of E8. When constructed from tetractyses, it has 6720 edges that are each lined by a pair of hexagonal yods, so that 13680 yods line its edges. The pairs of yods in the (70+70) polygons correspond to these pairs, whilst the 240 centres or shared yods correspond to the 240 vertices (for further discussion, see 4-d sacred geometries/Polychorons & Gosset polytope). We see that the tetractys construction of the 421 polytope has its exact parallel in the inner form of 10 Trees of Life. The 421 polytope can be regarded as the polytopic version of the inner form of 10 Trees of Life that map 10-d space-time, as well as the 10 whorls of the E8′-singlet state of the E8×E8′ heterotic superstring, whose subquark states were described over a century ago by C.W. Leadbeater.
The connection between music and the number
672
As 672 = 14×48, this number is the sum of the nine musical number weights
that surround the central number weight 48 in the Lambda Tetractys when all its numbers are
multiplied by 8:
|
8 |
|||
|
16 |
24 | ||
|
32 |
48 |
72 |
|
|
64 |
96 |
144 | 216 |
In fact, two different combinations of weights add up to 336 as well:
24 + 72 + 96 + 144 = 336 = 8 + 16 + 32 + 64 + 216.
The sum of all 10 weights = 15×48 = 720, which is the number of yods surrounding the centres of the seven separate Type B polygons:
|
|
|
|
The sum of the weights at its corners = 8 + 64 + 216 = 288, which is the number of yods surrounding the centres of the seven separate Type A polygons:
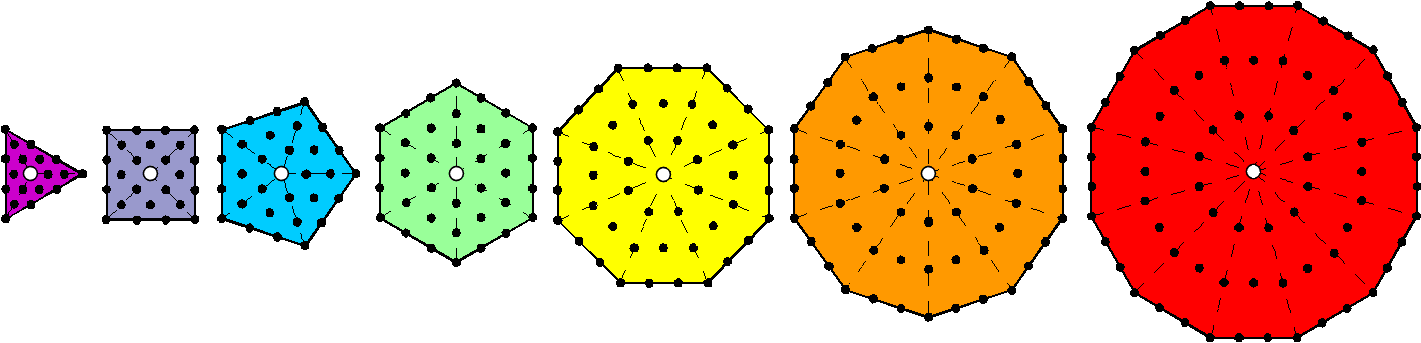 |
|
|
This is also the number of black hexagonal yods lining the three internal sides of tetractyses in each of their 48 sectors. It is also the sum of the three numbers added when the Lambda becomes the Lambda Tetractys: 48 + 96 + 144 = 288. The number 48 denotes the 48 red corners of the seven polygons, the number 96 denotes the 96 blue hexagonal lining their sides and the number 144 denotes the 144 green yods inside them that surround their centres when they are Type A. The sum of the seven weights forming the Lambda is the number of yods (432) added when the Type A polygons become Type B polygons. The number 672 is the number of yods that are not polygonal corners, i.e., it is the number of extra yods needed to construct from tetractyses the Type B polygons in the inner Tree of Life. This clearly demonstrates its character as a structural parameter of the inner Tree of Life. It is the sum of the nine weights that surround the number weight 48 at the centre of the Lambda Tetractys corresponding to this number, which is the tone ratio of the perfect fifth of the sixth octave, as well as the fourteenth overtone of the Pythagorean musical scale. In general, the sum (14n) of the nine weights lining the Lambda Tetractys with n at its centre cannot be the tone ratio of a note in the Pythagorean scale because all such notes have tone ratios of the form 2p3q (p = 0, ±1, ±2, etc; q = 0, ±1. ±2, etc), which therefore cannot contain a prime number such as 7, one of the factors of this sum. So the number 672 and the number 336 (sum of the nine number weights with 24 at the centre) are not tone ratios. For the same reason, this is true for the structural parameters 1680 (=5×336) and 2016 (=6×336) of the whorls of, respectively, the E8′-singlet and E8-singlet states of the E8×E8′ heterotic superstring.
The connection between the number 672 and the 144
Polyhedron
The polyhedral counterpart of the seven separate Type B polygons of the inner Tree of Life is the 144 Polyhedron.
This is one of the two polyhedra that make up the Polyhedral Tree of Life (see here). Their 120 and 144 faces are symbolised by the 120 boundary yods
and the 144 internal yods of the seven enfolded, Type A polygons. As was illustrated above, the 720 yods
surrounding the centres of these Type B polygons comprise the 288 yods that belong to them when they are Type A
and the 432 yods required to turn the Type A polygons into Type B polygons. Compare this with the 720
geometrical elements in the 144 Polyhedron that surround its axis:
The geometrical composition of the 144 Polyhedron
"2" denotes either the
vertices at the ends of the axis or its two segments)
|
Vertices |
Edges/sides |
Triangles |
Total |
|
| Exterior |
2 + 72 |
216 |
144 |
2 + 432 |
| Interior |
0 |
2 + 72 |
216 |
2 + 288 |
| Total |
2 + 72 |
2 + 288 |
360 |
4 + 720 |
The 288 yods correspond to either the 288 vertices & edges in its 144 faces or its 288 internal sides & triangles. The 432 yods correspond, respectively, to either the 432 geometrical elements that are internal/triangles in its faces or the 432 geometrical elements in its faces. The correspondence goes deeper than this because:
Surrounding the axis of the 144 Polyhedron are (720−48=672) points, lines & triangles other than the 48 vertices of tetrahedra. Including the two segments of the axis, it has 650 (= 65×10) lines & triangles, where 65 is the number value of ADONAI, the Godname of Malkuth. The Godname YAHWEH with number value 26 prescribes the 26 vertices of the disdyakis dodecahedron.
The connection between the number 672 and the
421 polytope
The 421 polytope discussed in 4-d sacred geometries is an 8-d polytope
whose 240 vertices have Cartesian coordinates that are those of the 240 roots of E8, the rank-8
exceptional Lie group:
 |
 |
Its 240 gauge charges are spread, 24 to a whorl, along the ten whorls of the E8×E8′ heterotic superstrings described by Besant, Leadbeater & Cowen. The polytope has 6720 (=10×672) edges of its triangular faces, which are nine times as many, so that its faces are composed of 67200 (=100×672) lines & triangles. Here is spectacular evidence of how this polytope, known since 1900 to represent the vertices of E8, possesses the same structural parameter 672 that appears in the inner Tree of Life and in its dodecagons, the Platonic solids and the Sri Yantra, as well as — according to micro-psi observations — in one revolution comprising 336 turns of the helical whorls in either type of observed particle. Even more spectacular is the fact that the 10 whorls of the UPA have (10×336=3360) circular turns in each revolution, that is, 6720 plane waves, and this is exactly the number of edges of the 421 polytope — the polytope whose vertices represent the roots of the very symmetry group that describes the unified force between E8×E8′ heterotic superstrings! How can anyone dismiss that as coincidence and still deny, despite all this supporting evidence, that the UPA is an E8×E8′ heterotic superstring? Admittedly, it still does not amount to a complete, theoretical explanation of the structure of the remote-viewed subquark or the basic particle of shadow matter. But no one can deny that some of the mathematical ingredients for such an explanation have been provided here, otherwise he or she has to dismiss the appearance of the same numbers in numerous contexts as pure coincidence — an extraordinary conjunction of improbable circumstances that most reasonable people would regard as impossible to believe. Both the existence of the 421 polytope and its basic properties have been known for over 120 years, and sceptics cannot be expected to be taken seriously if they believe that they can summarily dismiss as due to chance the fact that the number of its edges is exactly the number of sinusoidal wave components of the circularly polarised oscillations making up each revolution of all whorls of the E8′-singlet state of the E8×E8′ heterotic superstring, as implied in remote-viewing accounts of this particle that are even older than the discovery of this polytope.
| << Previous 1 2 [3] 4 5 ...24 Next >> |