ARTICLE 60

by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
|
According to the Tetrad Principle, the seven regular polygons making up the inner Tree of Life should acquire a special status when they are Type C because this variety of polygon is the fourth, starting from a bare polygon. This article analyses each Type C polygon and the sets of seven Type C polygons when separate and when enfolded. The Type C triangles embody the superstring structural parameter 168 and the dimension 248 of E8, the rank-8, exceptional Lie group describing the symmetry of the forces of one of the five types of superstrings. The two Type C squares embody the superstring structural parameter 336. The Type C pentagon embodies both the number 137 determining the fine-structure constant and the number of bones in the adult human skeleton. The two Type C hexagons embody the dimension 496 of E8×E8. A single Type C octagon embodies the number 336. The two Type C decagons embody the superstring structural parameter 840. The Type C dodecagon embodies the number 336. The (7+7) Type C polygons separated by the root edge have 496 corners of triangles. The superstring structural parameter 1680 is the number of hexagonal yods inside the seven separate Type C polygons. The Godnames ADONAI, YAHWEH, ELOHIM & ELOHIM SABAOTH prescribe the inner Tree of Life when its polygons are Type C. Representing by a Tree of Life each of the five revolutions made by each of the 10 whorls of the UPA/subquark superstring, the triangles making up the first (6+6) Type C polygons enfolded in 50 Trees have 16800 corners that correspond to the 16800 turns in the 10 helical whorls. The inner form of a single Tree of Life embodies the number 1680 as the number of corners & sides of triangles outside the root edge that are not shared with its outer form and which are not pure corners of polygons. |
1
Table 1. Gematria number values of the ten Sephiroth in the four Worlds.
ANGELS
CHAKRA1
Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the
Presence)
314Chaioth ha Qadesh
(Holy Living
Creatures)
833Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
6362
Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the
Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of
the Zodiac)
1403
Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50Tzaphkiel
(Contemplation
of God)
311Aralim
(Thrones)
282Shabathai
Rest.
(Saturn)
317Daath
(Knowledge)
4744
Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence
of God)
62Chasmalim
(Shining Ones)
428Tzadekh
Righteousness.
(Jupiter)
1945
Geburah
(Severity)
216ELOHA
(The Almighty)
36Samael
(Severity of God)
131Seraphim
(Fiery Serpents)
630Madim
Vehement Strength.
(Mars)
956
Tiphareth
(Beauty)
1081YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101Malachim
(Kings)
140Shemesh
The Solar Light.
(Sun)
6407
Netzach
(Victory)
148YAHWEH SABAOTH
(Lord of Hosts)
129Haniel
(Grace of God)
97Tarshishim or
Elohim
1260Nogah
Glittering Splendour.
(Venus)
648
Hod
(Glory)
15ELOHIM SABAOTH
(God of Hosts)
153Raphael
(Divine Physician)
311Beni Elohim
(Sons of God)
112Kokab
The Stellar Light.
(Mercury)
489
Yesod
(Foundation)
80SHADDAI EL CHAI
(Almighty Living
God)
49, 363Gabriel
(Strong Man of
God)
246Cherubim
(The Strong)
272Levanah
The Lunar Flame.
(Moon)
8710
Malkuth
(Kingdom)
496ADONAI MELEKH
(The Lord and King)
65, 155Sandalphon
(Manifest Messiah)
280Ashim
(Souls of Fire)
351Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
168
The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Orders of Angels and Mundane Chakras (their physical manifestation). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a number value to a word that is the sum of the numbers of its letters. Numbers from the table are written in boldface in the article.
2
1. Properties of the seven separate Type C polygons
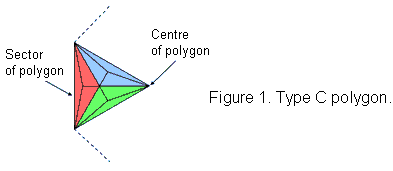
A polygon is Type C when its sectors are Type B triangles with seven corners & 15 sides of nine triangles, i.e., 31 geometrical elements, where 15 is the number value of YAH, the Godname of Chokmah, and 31 is the number value of EL,
the Godname of Chesed (Fig. 1). This means that each sector contributes 28 geometrical elements (5 corners, 14 sides & 9 triangles). The numbers of geometrical elements in a Type C n-gon (note that it need not be regular) are:
Number of corners ≡ C = 5n + 1
Number of sides ≡ S = 14n
Number of triangles ≡ T = 9n
Total = 28n + 1
("+1" denotes the centre of the polygon). The number of hexagonal yods ≡ H = 2S + T = 37n. The number of corners of the 9n tetractyses = C = 5n + 1. The number of yods ≡ Y = C + H = 42n + 1. The number of yods on sides of tetractyses ≡ B = C + 2S = 33n + 1. Table 2 and Table 3 below tabulate the geometrical and yod compositions of the seven separate Type C polygons that make up the inner form of the Tree of Life ("+7" refers to their seven centres):
Table 2. Number of geometrical elements in the 7 separate Type C polygons.
Triangle
(n=3)Square
(n=4)Pentagon
(n=5)Hexagon
(n=6)Octagon
(n=8)Decagon
(n=10)Dodecagon
(n=12)Total
Corners
16=15+1
21=20+1
26=25+1
31=30+1
41=40+1
51=50+1
61=60+1
247=240+7
Sides
42
56
70
84
112
140
168
672
Triangles
27
36
45
54
72
90
108
432
Total
85=84+1
113=112+1
141=140+1
169=168+1
225=224+1
281=280+1
337=336+1
1351=1344+7
Table 3. Number of yods in the 7 separate Type C polygons.
Triangle
(n=3)Square
(n=4)Pentagon
(n=5)Hexagon
(n=6)Octagon
(n=8)Decagon
(n=10)Dodecagon
(n=12)Total
C
16=15+1
21=20+1
26=25+1
31=30+1
41=40+1
51=50+1
61=60+1
247=240+7
H
111
148
185
222
296
370
444
1776
B
100=99+1
133=132+1
166=165+1
199=198+1
265=264+1
331=330+1
397=396+1
1591=1584+7
Y
127=126+1
169=168+1
211=210+1
253=252+1
337=336+1
421=420+1
505=504+1
2023=2016+7
CommentsTriangle
The Type C triangle has 85 geometrical elements (84 surrounding its centre), where
85 = 40 + 41 + 42 + 43
and
84 = 12 + 32 + 52 + 72.
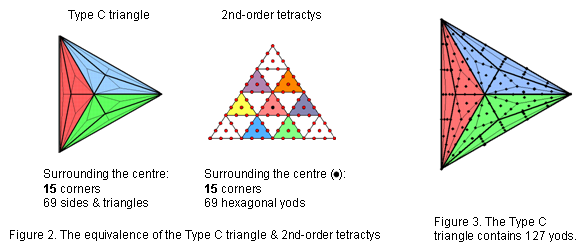
It has 15 corners and 69 sides & triangles surrounding its centre (Fig. 2). Compare this with the 2nd-order tetractys (Fig. 3). It has 85 yods consisting of 15 corners and 69 hexagonal yods that surround its centre:
3
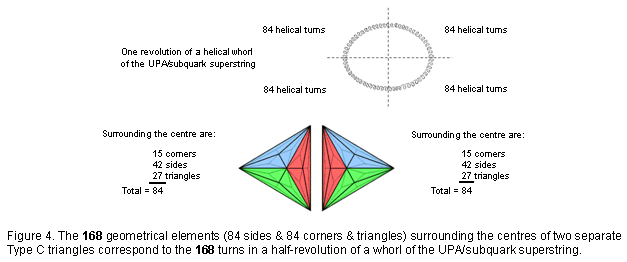
As the first stage in the sequence of development of the seven regular polygons making up the inner Tree of Life, the triangle embodies the pattern of this Pythagorean representation of holistic systems. The two separate Type C triangles have 168 geometrical elements surrounding their centres (Fig. 4). They embody the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth. This is a structural parameter of the subquark superstring, being the number of turns of each
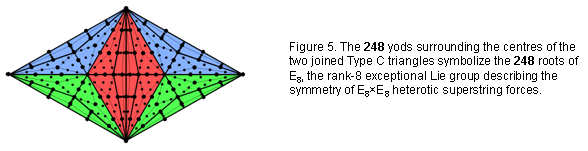
half-revolution of a whorl of the UPA. The Type C triangle has 127 yods, where 127 is the 31st prime number and 31 is the number of EL, the Godname of Chesed. The two joined Type C triangles have 246 yods outside their shared side, where 246 is the number value of Gabriel, the Archangel of Yesod. 248 yods surround their centres, where 248 is both the number value of Raziel, the Archangel of Chokmah, and the dimension of E8, the rank-8 exceptional Lie group. Alternatively, they have 248 yods that are intrinsic to them in the sense that they are unshared with the outer Tree of Life, their left-hand and right-hand corners coinciding with, respectively Geburah and Chesed (Fig. 5). Embodied in the Type C triangle are both the structural and the dynamical parameters of a superstring!
Square
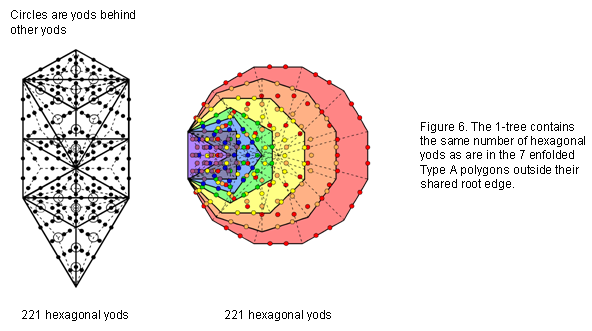
The two joined Type C squares have 221 geometrical elements surrounding their centres. This is the4
number of hexagonal yods in the 1-tree and in the seven enfolded Type A polygons outside their shared root edge (Fig. 6).
Figure 7. 168 yods surround the centre of the Type C square.
Surrounding the centre of each separate Type C square are 168 yods (Fig. 7). Whereas both triangles are needed to embody this superstring structural parameter, the square on its own achieves this.
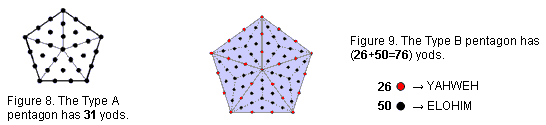
Pentagon
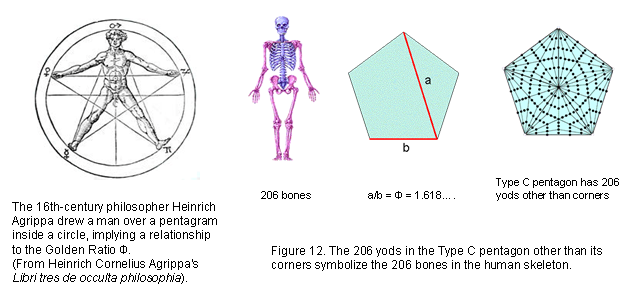
A Type A pentagon has 31 yods (Fig. 8). It is a representation of EL ("God"), the Godname of Chesed with number value 31. The yod at its centre A denotes the letter aleph א (E) with gematria value 1 and the 30 yods surrounding it express the value
30 of the letter lamed ל (L). The Type B pentagon has 76 yods (Fig. 9). This is the number value of YAHWEH ELOHIM, the Godname of Tiphareth. The number 26 of YAHWEH is the number of red yods lining the sides of the five basic sectors of the Type C pentagon. The number 50 of ELOHIM is the number of black yods. These embodiments of two well-known Godnames are described here to set the stage for the later discussion of how the pentagon embodies the number of bones in the adult human skeleton and the number 137 that determines the fine-structure constant at the heart of quantum electrodynamics, the highly successful theory of electromagnetic interactions.
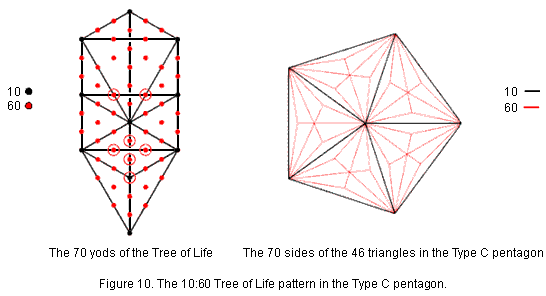
The Type C pentagon (Fig. 10) has 26 corners & 70 sides of 45 triangles, i.e., 141 geometrical elements. Two separate Type C pentagons have 282 geometrical elements, of which 50 are corners surrounding
5
their centres. 282 is the number value of Aralim, the Order of Angels assigned to Binah, whose Godname ELOHIM has the number value 50. The number 70 is a parameter of holistic systems, being the number of yods in the Tree of Life when its 16 triangles are tetractyses. The five black sides of the pentagon and the five black sides of its sectors correspond to the (5+5) Sephirothic corners of these triangles. The 60 remaining red sides of the 45 triangles correspond to the 60 hexagonal yods in the Tree of Life constructed from tetractyses. This 10:60 pattern expresses the difference between Malkuth and the six higher Sephiroth of Construction in the outer Tree of Life. Its counterpart in its inner form is the dodecagon and the six regular polygons that precede it.
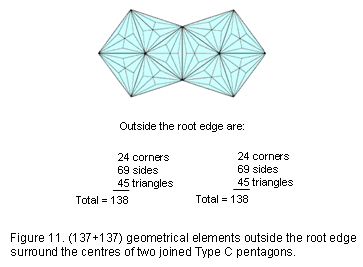
140 geometrical elements in the Type C pentagon surround its centre, where 140 is the number of Masloth, the Mundane Chakra of Chokmah, whose Godname YAHWEH has the number 26. 137 geometrical elements outside the root edge surround its centre (Fig. 11). We see that the geometrical composition of the Type C pentagon embodies the number 137 determining the fine-structure constant α = e2/ħc ≈ 1/137 well-known to physicists, whilst the number of bones in the adult human skeleton is embodied in its yods other than its corners (see here).
ELOHIM, the Godname of Binah, prescribes the pair of joined Type C pentagons because its number value 50 is the number of corners of their 90 triangles, whilst YAHWEH, the Godname of Chokmah with number value 26, prescribes the 26 corners of the 45 triangles in each pentagon. The two joined Type C pentagons have 229 lines & triangles, where 229 is the 50th prime number. ELOHIM prescribes both the number of corners of the triangles in the two pentagons and the number of their sides & triangles!
The pair of joined Type C pentagons has 189 corners & sides, i.e., 187 corners & sides surround their two centres. 187 is the number of Auphanim, the Order of Angels assigned to Chokmah. 95 corners & sides in a Type C pentagon surround its centre, where 95 is the number value of Madim, the Mundane Chakra of Geburah. A corner of each pentagon coincides with the centre of the decagon when it is part of the inner Tree of Life. This means that surrounding the centre of each pentagon are 136 geometrical elements outside the shared root edge that are intrinsic to this polygon in the sense that they are not part of any other polygon in the inner Tree of Life. The pair of pentagons has 272 such geometrical elements, where 272 is the number value of Cherubim, the Order of Angels assigned to Yesod.
The Type C pentagon has 211 yods, that is, 210 (=21×10) yods surround its centre. 21 is the number
6
value of EHYEH, the Godname of Kether. It contains 206 yods other than its five defining corners (Fig. 12). In other words, given a pentagon, 206 more yods in 45 tetractyses (comprising 21 corners and 185 hexagonal yods) are needed to transform it into a Type C pentagon. This is how the pentagon, whose diagonal width a and side b are in the proportion of the Golden Ratio: a/b = Φ = (1+√5)/2 = 1.618..., embodies the number of bones in the adult human skeleton. Many artists through the centuries have believed that this famous ratio determines the relative proportions of parts of the ideal human body. Whatever the truth of this controversial claim, here is an indisputable, exact mathematical connection between its bone composition and the Golden Proportion Φ. Article 32 & Article 33 explain how the outer & inner Trees of Life embody the human axial and appendicular skeletons (see also Human skeleton). Article 36 shows how the disdyakis triacontahedron — the polyhedral form of the inner Tree of Life — embodies 206 yods symbolizing the 206 bones (see also here).
Hexagon
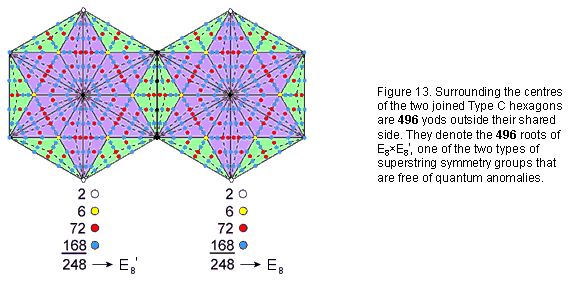
168 geometrical elements surround the centre of the Type C hexagon. They comprise 84 corners & triangles and 84 sides. Its geometrical composition displays the 84:84 division of this number that is characteristic of holistic systems. The Type C hexagon contains 222 hexagonal yods. This is the number of hexagonal yods associated with each set of seven enfolded
Type A polygons. 248 yods outside the shared root edge surround the centre of each hexagon (Fig. 13). This is the dimension of E8, the rank-8, exceptional Lie group. The two joined Type C hexagons embody the dimension 496 of E8×E8′. This is highly significant in view of the Tetrad Principle formulated in Article 1, for the Type C hexagon is the fourth in the series of this polygon, which is the fourth type of regular polygon:
Triangle → square → pentagon → hexagon → heptagon →...
Hexagon → Type A hexagon → Type B hexagon → Type C hexagon → Type D hexagon →....
7
Octagon
The octagon has 225 geometrical elements, so that the two joined octagons have 444 geometrical elements outside their shared side, 222 in each polygon. This is the number of hexagonal yods in the inner Tree of Life, 222 hexagonal yods being
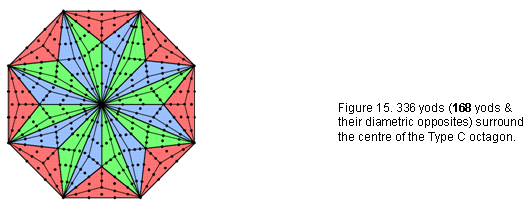
associated with each set of seven enfolded polygons (Fig. 14). 336 yods surround the centre of the octagon (Fig. 15). This is the number of turns in one revolution of each whorl of the UPA. The octagon embodies this major structural parameter of the
subquark superstring. Surrounding its centre are 264 yods lining the sides of its 72 tetractyses. This is the yod population of
the seven enfolded Type A polygons (Fig. 16).
Decagon
280 geometrical elements comprising 50 corners, 140 sides and 90 triangles surround the centre of the decagon. 840 yods surround the centres of two separate decagons. This is the number of turns in an outer or inner half of a whorl of the UPA.
Dodecagon
336 geometrical elements (168 corners & triangles, 168 sides) surround the centre of a dodecagon. This is the number of yods other than corners in two joined Type B dodecagons (Fig. 17). The number 168 factorises in the geometrical case as 12×14 — exactly as it does for the yods in each Type B dodecagon,
8
each sector contributing 14 yods other than corners. The holistic division 336 = 168 + 168 arises because the number of corners & triangles in any Type C polygon is equal to the number of sides (as is the case for Type A & Type B polygons). The dodecagon has 444 hexagonal yods — exactly the same as for the inner Tree of Life. 504 yods surround its centre (Fig. 18). They comprise 168 black yods (the number of yods in a Type B dodecagon other than the corners of its sectors) and
(2×168=336) red yods. The superstring/UPA significance of this is discussed here under the heading "TYPE C DODECAGON", here and here. The way in which the heptagon and outer Tree of Life embody the number 504 is discussed here. The fact that the dodecagon is the first single polygon to embody superstring structural parameters in terms of both its geometrical and yod compositions (the hexagon does the same but only as two separate polygons) confirms its unique status as the polygonal version of the outer Tree of Life. 500 (=50×10) yods outside the root edge surround its centre. This is how ELOHIM, the Godname of Binah with number 50, prescribes the yods that construct the dodecagon. Surrounding the centres of the two joined dodecagons (the tenth regular polygon) are (1000=103) yods outside the root edge. This illustrates the power of the Decad.
Properties of the seven separate polygons
9
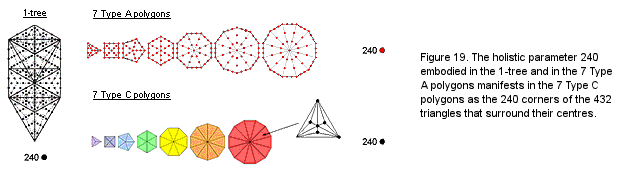
there are 496 corners present. Associated with each set are 248 corners (240 corners of triangles, 7 centres & one endpoint). This 248:248 pattern represents the (248+248=496) roots of E8×E8′, one of the two symmetry groups of heterotic superstrings.
2. Properties of the seven enfolded polygons
When the seven regular polygons of the inner Tree of Life are enfolded in one another, a corner of the triangle coincides with the centre of the hexagon and a corner of the pentagon coincides with the centre of the decagon. All the 31 geometrical elements in the sector of the hexagon replaced by the triangle disappear, so that, instead of 169 geometrical elements (see table above). the hexagon is now left with five sectors containing (169–31=138) elements. 46 yods also disappear from this sector because it is a Type A triangle with 46 yods, so that, instead of 253 yods, the hexagon is left with (252–46=207) yods.
Tabulated below in Tables 4 & 5 are the geometrical and yod compositions of the seven enfolded Type C polygons outside their shared root edge.
Table 4. Number of geometrical elements outside the root edge in the 7 enfolded Type C polygons.
Triangle
(n=3)Square
(n=4)Pentagon
(n=5)Hexagon
(n=6)Octagon
(n=8)Decagon
(n=10)Dodecagon
(n=12)Total
Corners
14
19
24
24
39
48
59
227
Sides
41
55
69
69
111
139
167
651
Triangles
27
36
45
45
72
90
108
423
Total
82
110
138
138
222
277
334
1301
Table 5. Number of yods outside the root edge in the 7 enfolded Type C polygons.
Triangle
(n=3)Square
(n=4)Pentagon
(n=5)Hexagon
(n=6)Octagon
(n=8)Decagon
(n=10)Dodecagon
(n=12)Total
C
14
19
24
24
39
48
59
227
H
109
146
183
183
294
368
442
1725
B
96
129
162
162
261
326
393
1529
Y
123
165
207
207
333
416
501
1952
Comments
10
49th prime number, showing how EL ChAI, the Godname of Yesod with number value 49, prescribes the skeletal shape of the seven enfolded Type C polygons. Including the two endpoints of the shared root edge, there are 229 corners. The Godname ELOHIM with number value 50 prescribes the number of corners because 229 is the 50th prime number. This is a spectacular illustration of the power of Godnames at work in mathematically determining the geometry of the inner Tree of Life.
14 24 24 1300 = 15 + 25 + 35 + 45 =
34 34 34 44
44 44 44
This means that 2600 geometrical elements are intrinsic to both sets of seven enfolded polygons, where2600 = 512 − 1 = 3 + 5 + 7 + ... + 101
is the sum of the first 50 odd integers after 1. This shows how both ELOHIM with number value 50 and YAHWEH with number value 26 prescribes how many intrinsic geometrical elements are needed to construct the (7+7) enfolded polygons, starting with the root edge. Such beautiful harmony between number and geometry is powerful evidence of the archetypal status of this sacred geometry.
Outside the root edge are 227 corners of the 423 triangles in the seven enfolded polygons. The dodecagon has 59 such corners, so that the first six enfolded polygons have 168 such corners of 315 triangles. Both sets of the first six enfolded polygons, which have 50 polygonal corners, have (168+168=336) corners of 630 triangles outside the root edge, where 630 is the number value of Seraphim, the Order of Angels assigned to Geburah. ELOHIM, the Godname of Binah with number value 50, prescribes the superstring structural parameter 336, which is the number of turns in each of the 50 revolutions of the ten whorls of the UPA about its spin axis. Including the two endpoints of the root edge, the first (6+6) enfolded polygons have 338 corners. But
11
the topmost corners of their two hexagons coincide with the lowest corners of the hexagons enfolded in the next higher Tree of Life. This means that 336 corners are intrinsic to each set of (6+6) enfolded polygons. The number of intrinsic corners of the first (6+6) polygons enfolded in n Trees of Life = 336n. The 120 such polygons enfolded in 10 overlapping Trees have 3360 intrinsic corners. This is the number of turns per revolution in all ten whorls of the UPA. Each revolution of a whorl can be represented by a Tree of Life, so that 50 overlapping Trees represent the 50 revolutions of the whorls of the UPA. The 600 polygons of the first six types enfolded in them have (336×50=16800) intrinsic corners. This is the number of turns in the ten whorls of the UPA. The five sets of 10 Trees making up 50 Trees correspond to the five revolutions of 10 whorls. These Type C polygons provide a geometrical representation of the UPA/subquark superstring because the first six polygons constitute a holistic subset of the complete set of seven polygons, as has been illustrated many times elsewhere in this website. The fact that the first six polygons of the inner Tree of Life have 36 corners when separate and 26 corners when enfolded, both enfolded sets having 50 corners serves to illustrate how they are prescribed by the Godnames of the ten Sephiroth (see Article 8 for more details).
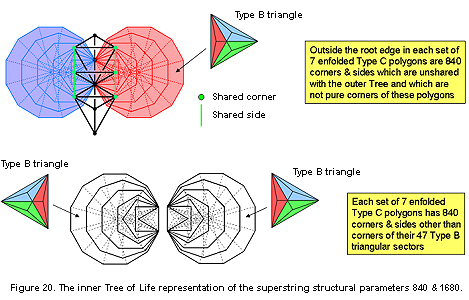
The 423 triangles in the seven enfolded polygons have 881 corners & sides. There are five corners & sides on the vertical axis of the hexagon that are shared with the outer Tree of Life as its Pillar of Mercy (they are coloured green in Figure 20). Similarly for the hexagon in the other set of polygons, five corners & sides coincide with the Pillar of Judgement. One of these corners is the centre of the hexagon, so that (881−5−6=870=87×10) intrinsic corners & sides surround the centres of the seven enfolded polygons. 87 is the number value of Levanah, the Mundane Chakra of Yesod. 878 corners & sides in each set of seven enfolded polygons are outside the root edge. Of these, five corners & sides are shared with the outer Tree, leaving 873 intrinsic corners & sides. Of these, five are centres of polygons that are not also corners and 28 corners are pure corners in the sense that none of them is also the centre of a polygon. Hence, the centres of each set of polygons are surrounded by (873−5−28=840) intrinsic corners & sides other than their corners. Outside the root edge of both sets of enfolded polygons are (840+840=1680) intrinsic corners & sides that are not pure corners of polygons. Alternatively, each set of seven enfolded polygons has (including the root edge) 881 corners & sides, of which 41 corners are corners of their 47 sectors, leaving 840 corners & sides, so that both separate sets have 1680 such corners & sides other than corners of sectors. Each set separately embodies the superstring structural parameter 840, whilst both sets of enfolded polygons embody the superstring structural parameter 1680. Ten overlapping Trees mapping the 10 whorls of the UPA have an inner form containing 16800 intrinsic corners & sides that are not pure corners of their (70+70) enfolded Type C polygons. This is the inner Tree of Life representation of the subquark state of the E8×E8 heterotic superstring.
12