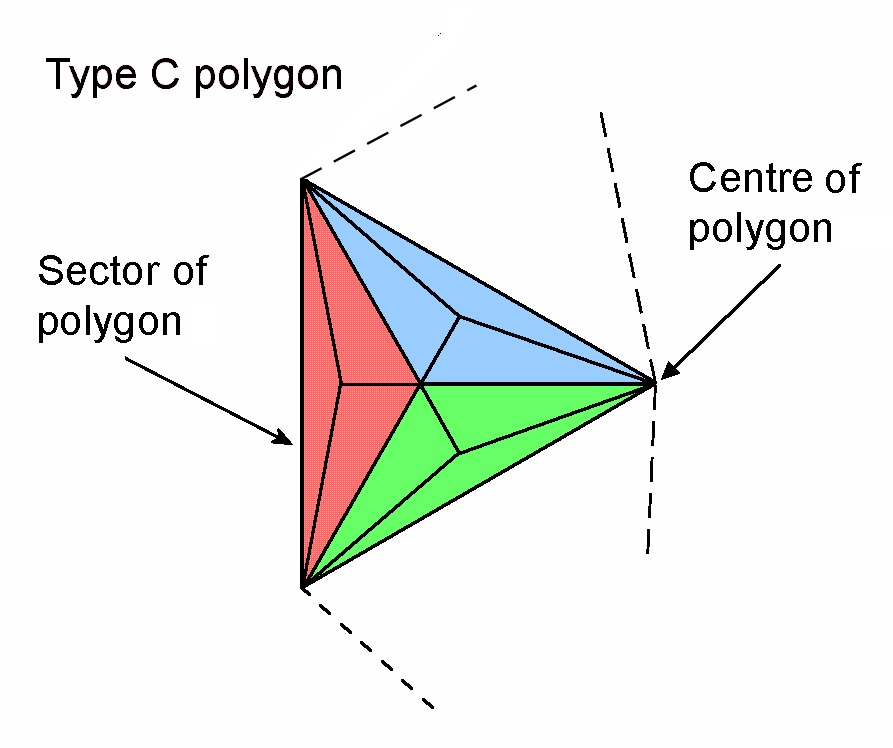
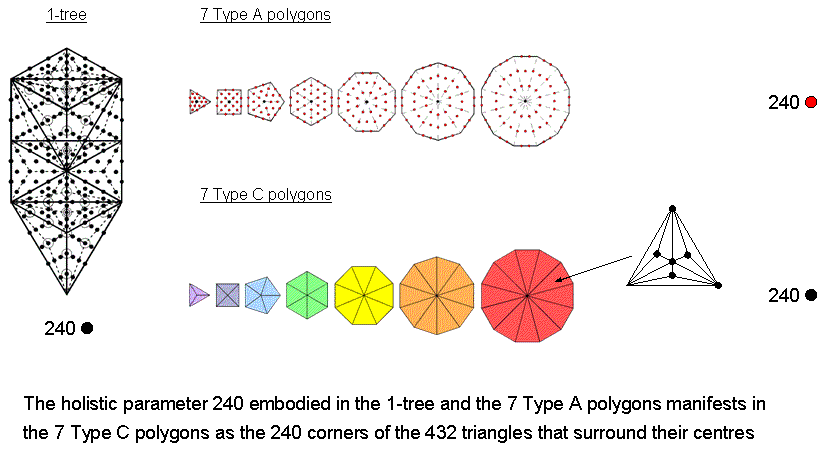
#29 Properties of the seven Type C polygons

A polygon is Type C when its sectors are Type B triangles with 7 corners & 15 sides of 9 triangles, i.e., 31 geometrical elements, where 15 is the number value of YAH, the Godname of Chokmah, and 31 is the number value of EL, the Godname of Chesed. This means that each sector contributes 28 geometrical elements (5 corners, 14 sides & 9 triangles). The numbers of geometrical elements in a Type C polygon with n sides (note that it need not be regular) are:

("+1" denotes the centre of the polygon). The number of hexagonal yods ≡ H = 2S + T = 37n. The number of corners of the 9n tetractyses = C = 5n + 1. The number of yods ≡ Y = C + H = 42n + 1. The number of yods on sides of tetractyses ≡ B = C + 2S = 33n + 1. Below are tabulated the geometrical and yod compositions of the seven separate Type C polygons that make up the inner form of the Tree of Life ("+7" refers to their seven centres):

 
Comments

Triangle
The Type C triangle has 85 geometrical elements (84 surrounding its centre), where

85 = 4⁰ + 4¹ + 4² + 4³

and

84 = 1² + 3² + 5² + 7².

It has 15 corners and 69 sides & triangles surrounding its centre. Compare this with the 2nd-order tetractys, which has 85 yods consisting of 15 corners of ten 1st-order tetractyses and 69 hexagonal yods that surround its centre:

As the first stage in the sequence of development of the seven regular polygons making up the inner Tree of Life, the triangle is the seed embodying the pattern of this Pythagorean representation of holistic systems that flowers in the dodecagon. The two separate Type C triangles have 168 geometrical elements surrounding their centres:

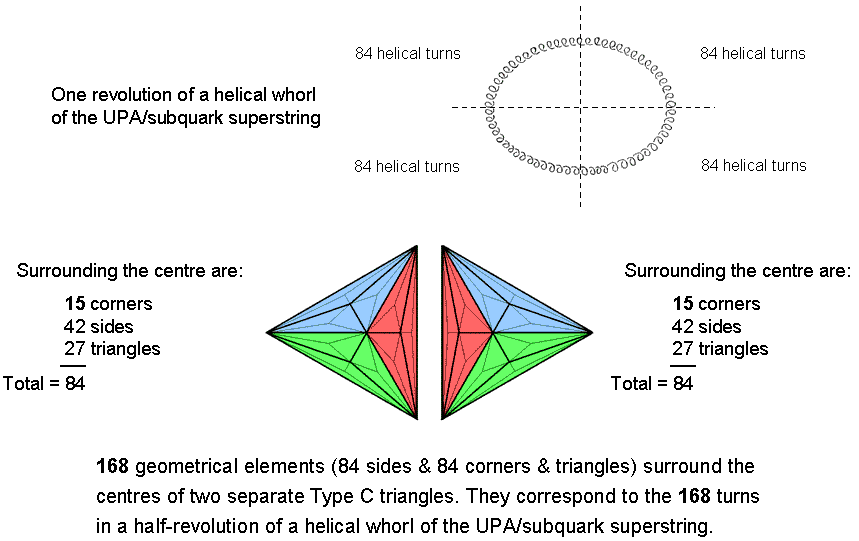
They embody the number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth. This is a structural parameter of the subquark superstring, being the number of turns of each half-revolution of a whorl of the UPA. The Type C triangle has 127 yods, where 127 is the 31st prime number and 31 is the number of EL, the Godname of Chesed. The two joined Type C triangles have 246 yods outside their shared side, where 246 is the number value of Gabriel, the Archangel of Yesod. 248 yods surround their centres, where 248 is both the number value of Raziel, the Archangel of Chokmah, and the dimension of E₈, the rank-8 exceptional Lie group. Alternatively, they have 248 yods that are intrinsic to them in the sense that they are unshared with the outer Tree of Life, their left-hand and right-hand corners coinciding with, respectively Geburah and Chesed when the outer & inner Trees of Life are superposed:

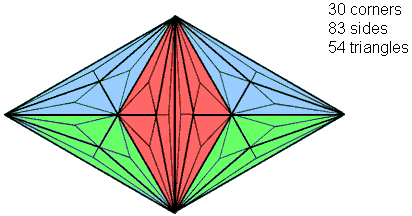
There are 248 yods in the two Type C triangles of the inner Tree of Life that are intrinsic to them because they are unshared with the outer Tree.	The two joined Type C triangles have 137 sides & triangles.

Embodied in the two separate and joined Type C triangles are, respectively, the structural and the dynamical parameters of an E₈×E₈′ superstring! (see also here). The two joined triangles have 137 sides & triangles. They also embody the number 137 determining the approximate value of the fine-structure constant α = e²/ħc ≅ 1/137. As was pointed out in #28, this number so important to atomic and particle physics is embodied in the Type C pentagon.

Square

The two joined Type C squares have 221 geometrical elements surrounding their centres. This is the number of hexagonal yods in the 1-tree and in the seven enfolded Type A polygons outside their shared root edge:

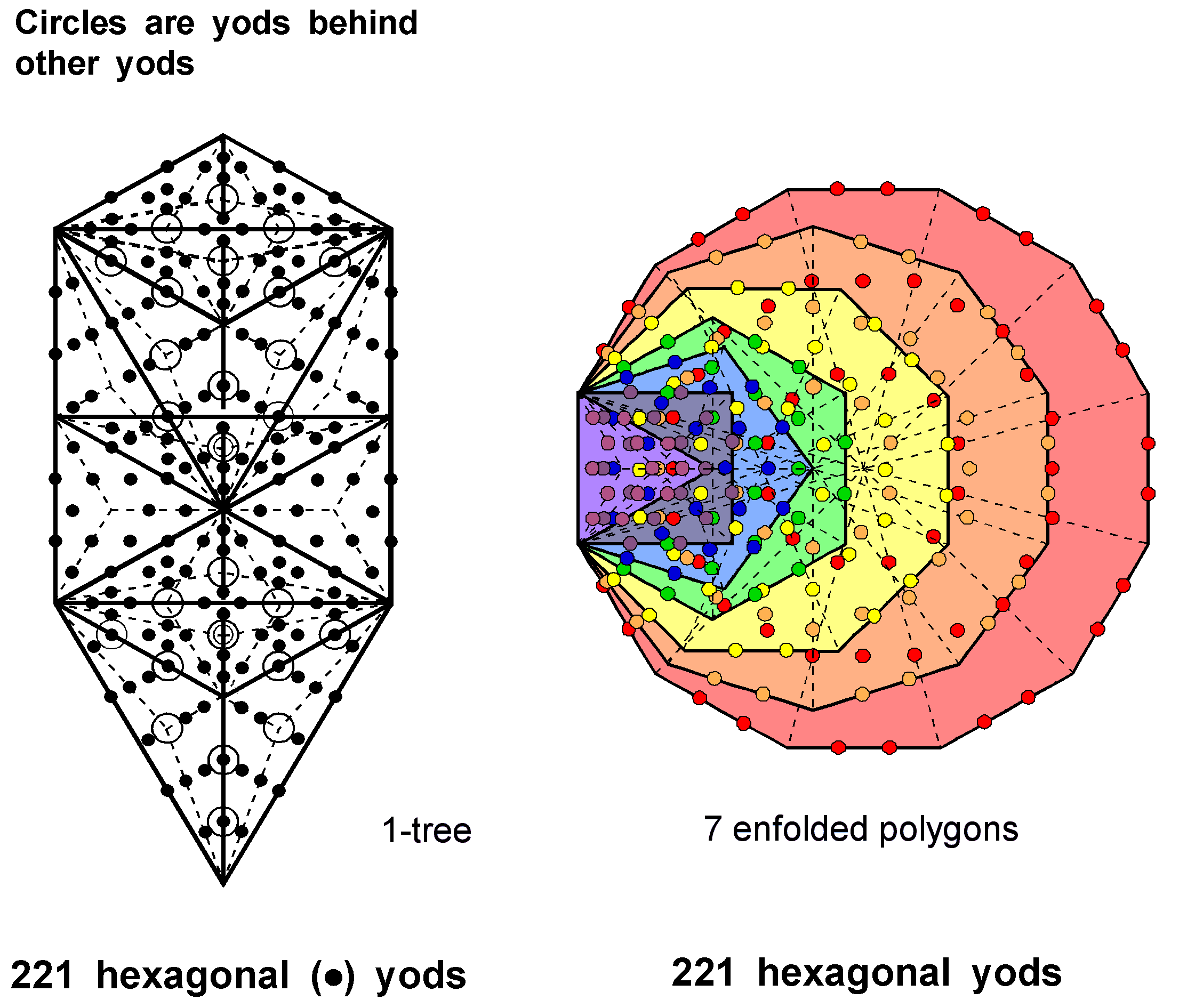
Surrounding the centre of each separate Type C square are 168 yods:

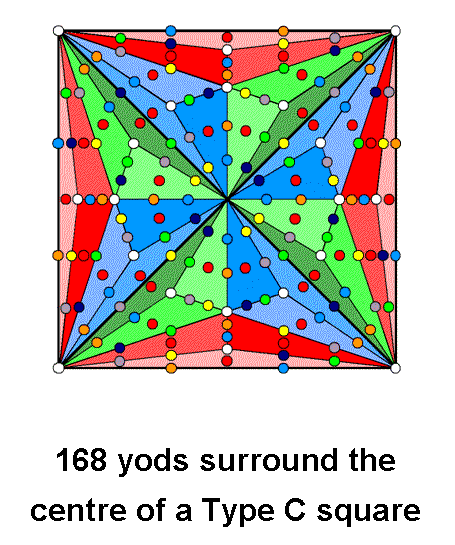
Whereas both separate triangles are needed to embody geometrically this superstring structural parameter, a single square achieves this in terms of its yod composition. It is a remarkable illustration of the Tetrad Principle formulated in Article 1, for the square has four corners and the Type C square is the fourth in the sequence:

Square → Type A square → Type B square → Type C square → ... .

Pentagon

How the pentagon embodies the 206 bones in the human adult skeleton was discussed in #27 of this section. How it embodies the fine-structure number 137 was discussed in #28.

Hexagon

168 geometrical elements surround the centre of the Type C hexagon. They comprise 84 corners & triangles and 84 sides. Its geometrical composition displays the 84:84 division of this number that is characteristic of holistic systems. The Type C hexagon contains 222 hexagonal yods. This is the number of hexagonal yods associated with each set of seven enfolded Type A polygons (see here). 248 yods outside the shared root edge surround the centre of each hexagon. The two Type C hexagons embody the dimension 496 of E₈×E₈′:

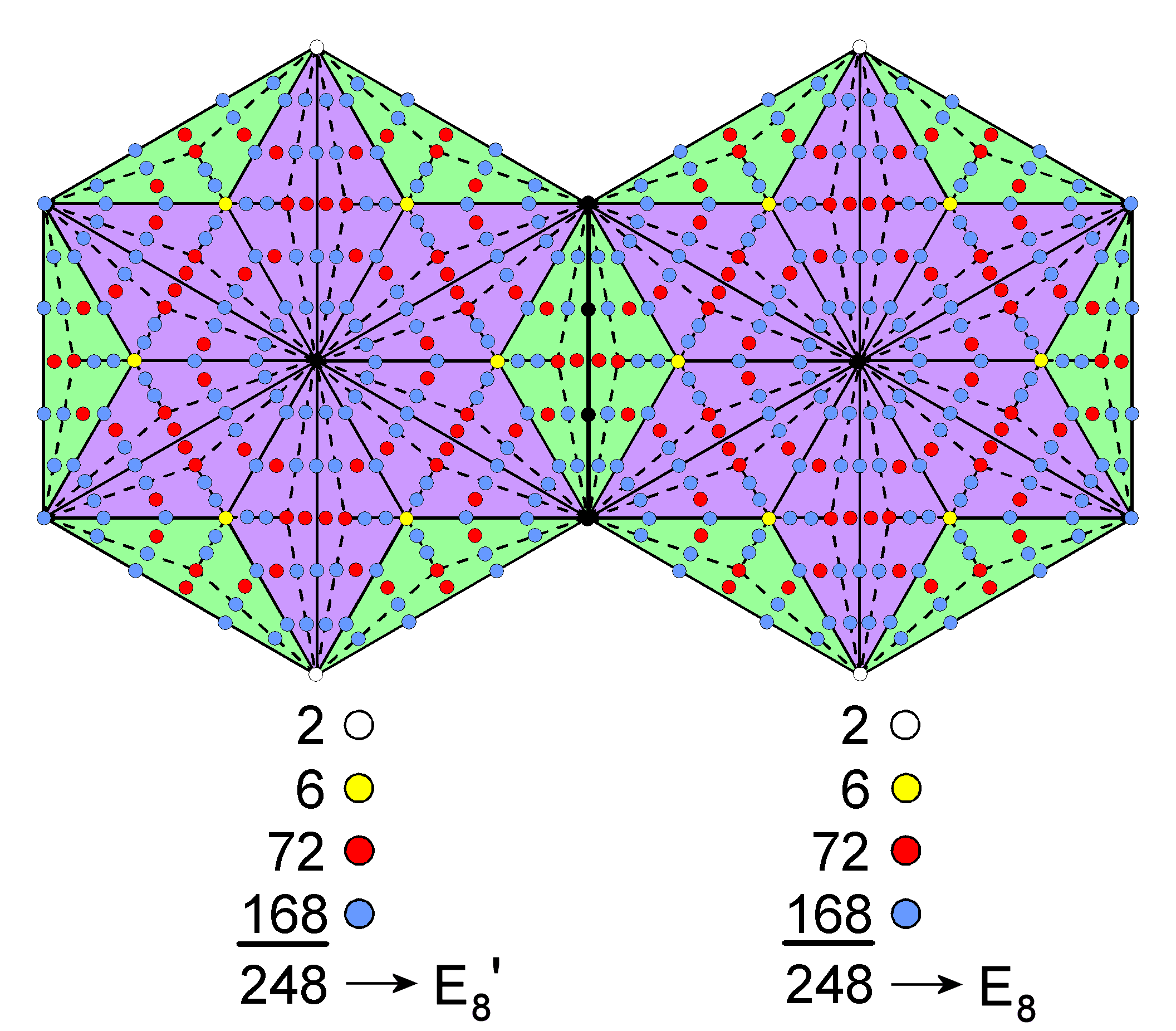
This is highly significant in view of the Tetrad Principle formulated in Article 1, for the Type C hexagon is the fourth in the series of this polygon, which is the fourth type of regular polygon:

Triangle → square → pentagon → hexagon → heptagon → ...

Hexagon → Type A hexagon → Type B hexagon → Type C hexagon → Type D hexagon →....

See #16 here for further discussion of this embedding in the hexagon of the root composition of the heterotic superstring symmetry group E₈×E₈′.

Octagon
The octagon has 225 geometrical elements, so that the two joined octagons have 444 geometrical elements outside their shared side, 222 in each polygon. This is the number of hexagonal yods in the inner Tree of Life, 222 hexagonal yods being associated with each set of seven enfolded polygons:

336 yods surround the centre of the octagon:

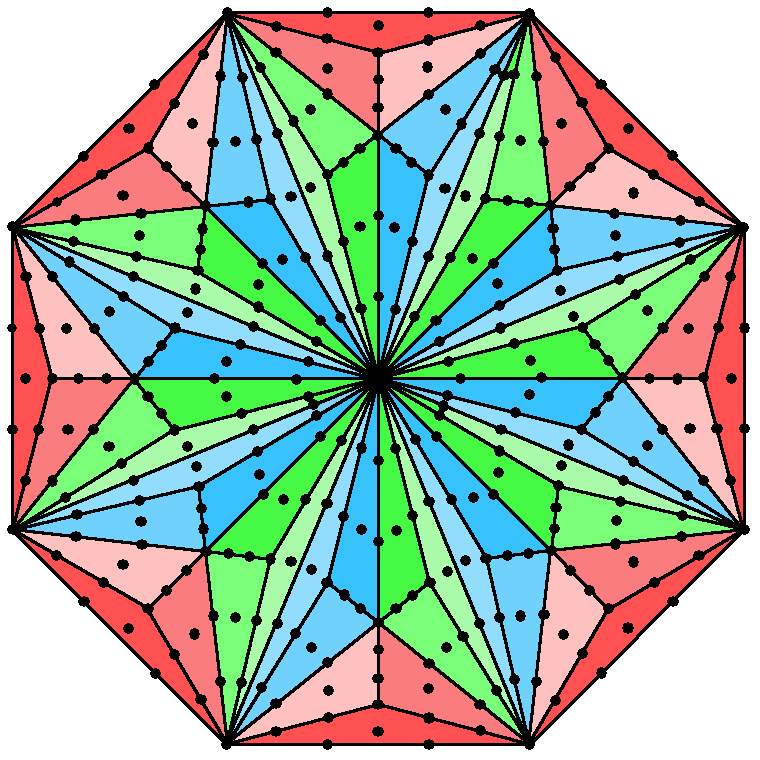
This is the number of turns in one revolution of each whorl of the UPA. The octagon embodies this major structural parameter of the subquark superstring. Surrounding its centre are 264 yods lining the sides of its 72 tetractyses. This is the yod population of the seven enfolded Type A polygons:

Decagon

280 geometrical elements comprising 50 corners, 140 sides and 90 triangles surround the centre of the decagon. 840 yods surround the centres of two separate decagons. This is the number of turns in an outer or inner half of a whorl of the UPA.

Dodecagon

336 geometrical elements (168 corners & triangles, 168 sides) surround the centre of a dodecagon. This is the number of yods other than corners in two joined Type B dodecagons:

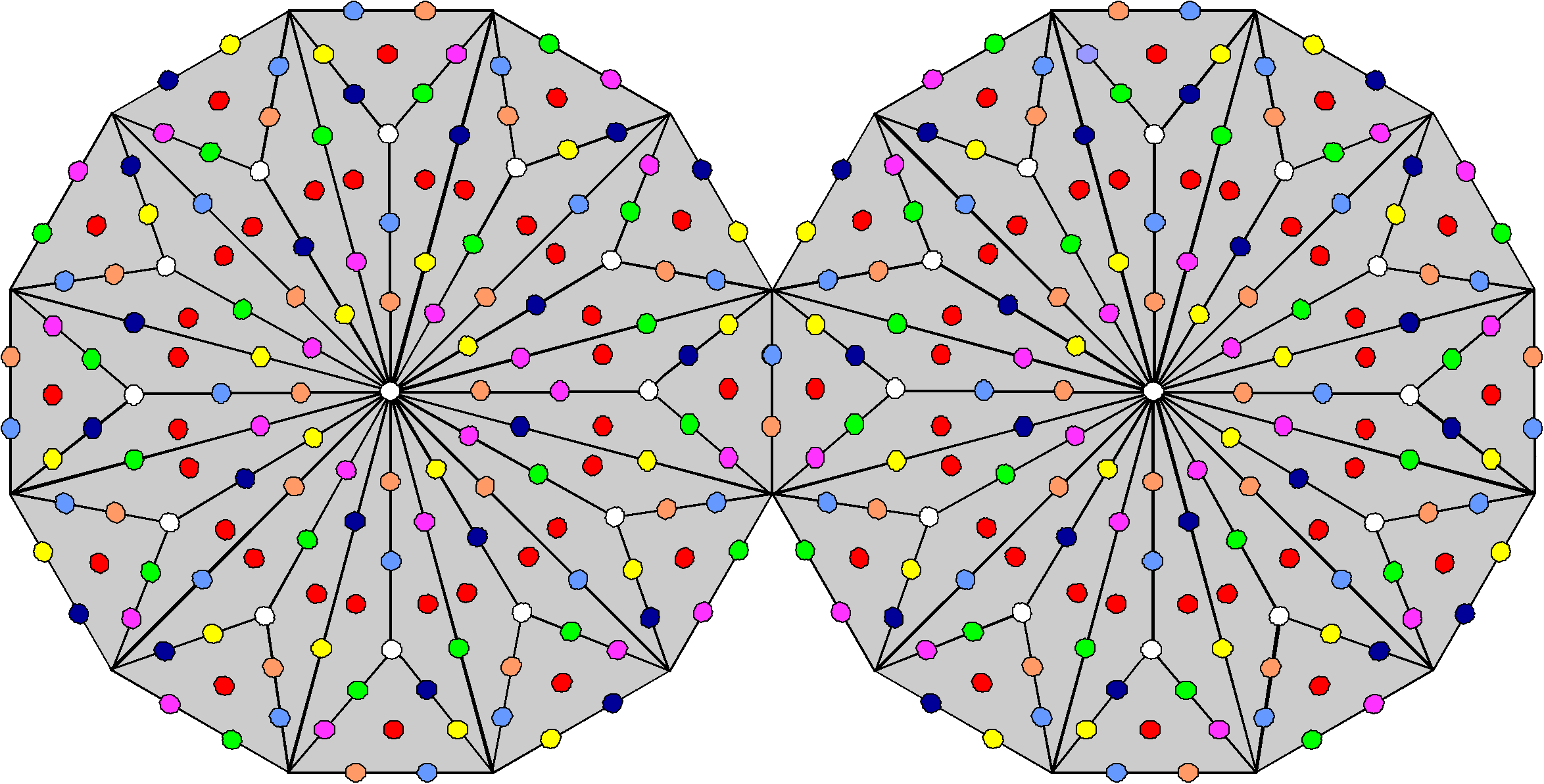
The number 168 factorizes in the geometrical case as 12×14 (12 sectors, 14 sides per sector) — exactly as it does for the yods in each Type B dodecagon, each sector contributing 14 yods other than corners. The holistic division: 336 = 168 + 168 arises because the number of corners & triangles (14n) surrounding the centre of any Type C polygon with n corners is equal to the number of sides (14n) of these triangles (as is the case for Type A & Type B polygons). The dodecagon has 444 hexagonal yods — exactly the same as for the inner Tree of Life. 504 yods surround its centre:

They comprise 168 black yods (the number of yods in a Type B dodecagon other than the corners of its sectors) and (2×168=336) red yods. The superstring/UPA significance of this is discussed here under the heading "TYPE C DODECAGON", as well as here and here. The way in which the heptagon and outer Tree of Life embody the number 504 is discussed here. The fact that the dodecagon is the first single polygon to embody superstring structural parameters in terms of both its geometrical and yod compositions confirms its unique status as the polygonal version of the outer Tree of Life. 500 (=50×10) yods outside the root edge surround its centre. This is how ELOHIM, the Godname of Binah with number 50, prescribes the yods that construct the dodecagon. Surrounding the centres of the two joined dodecagons (the tenth regular polygon) are (1000=10³) yods outside the root edge. This illustrates the power of the Decad to quantify properties of holistic systems.

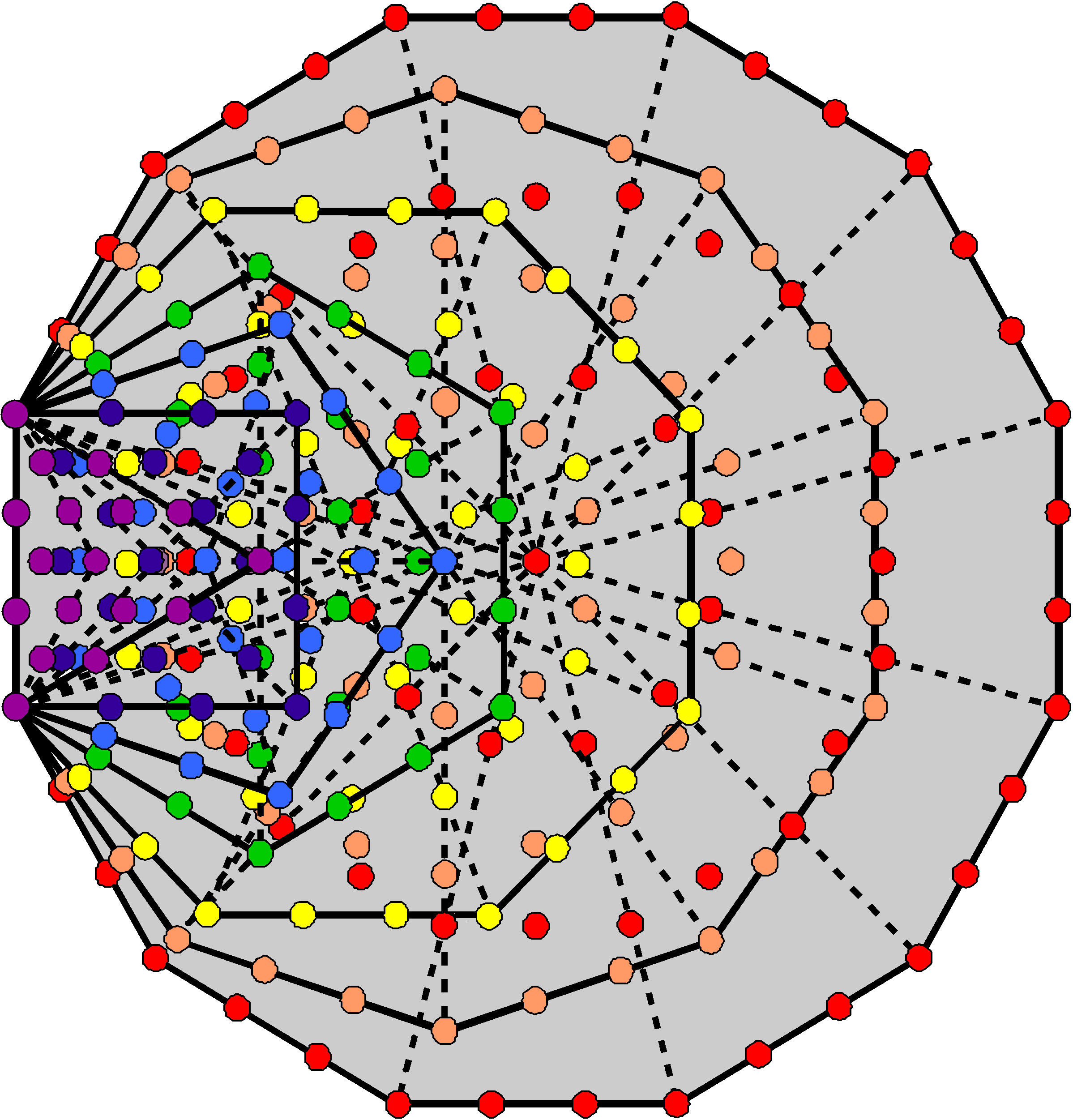
Properties of the seven separate Type C polygons

• 240 corners of 432 triangles with 672 sides surround the centres of the seven polygons. The number 240 is a parameter of holistic systems (see The holistic pattern under the heading "240 = 72 + 168"):

  

  For example, when the 19 triangles in the 1-tree are Type A, it contains 240 yods other than their 11 corners, whilst the seven separate Type A triangles contain 240 hexagonal yods. There are (240+240=480) corners of 864 triangles surrounding the 14 centres of the (7+7) Type C polygons, i.e., 494 corners in total. If we imagine the two sets of seven polygons separated by a straight line representing the root edge, whose endpoints count as corners, there are 496 corners present. Associated with each set are 248 corners (240 corners of triangles, 7 centres & one endpoint). This 248:248 pattern represents the (248+248=496) roots of E₈×E₈′, one of the two symmetry groups of heterotic superstrings.
• The seven separate polygons have 672 sides and 672 corners & triangles surround their centres. This number was encountered in the discussion here of the first four Platonic solids when their faces and interiors are constructed from tetractyses. It was found that they contain 672 yods, making an average of 168 yods per Platonic solid. Its manifestation in the highly complex, superstring-connected geometry of the 4₂₁ polytope is discussed in detail in 4-d sacred geometries.
• 1344 geometrical elements surround the centres of the seven polygons. This number is embodied in the (7+7) enfolded Type B polygons in the following way: when the outer and inner Trees of Life are superposed, the two side pillars lie in the plane of the polygons, coinciding with the vertical axes of the two hexagons. Each axis contains seven yods shared with a hexagon. One of these is its centre, leaving six other centres. Each set of seven enfolded polygons contain (7+6=13) yods that are either shared yods or centres. Both sets of polygons have 1370 yods, of which 26 are such yods, leaving 1344 yods intrinsic to the polygons that surround their centres.
• A Type C n-gon contains 37n hexagonal yods. 2n hexagonal yods line its n sides, inside which are 35n hexagonal yods. The number of hexagonal yods inside the seven Type C polygons = ∑35n = 35∑n = 35×48 = 1680. This is the number of turns in each helical whorl of the UPA. Embodied, therefore, inside the seven separate polygons is this major structural parameter of the subquark superstring. 840 hexagonal yods are inside the dodecagon and the first three polygons (triangles, square & pentagon) and 840 hexagonal yods are inside the next three polygons (hexagon, octagon & decagon). The characteristic 24:24 division of the holistic parameter 48 manifests in the inner Tree of Life as the 840 hexagonal yods inside each of these sets of polygons with 24 corners. This manifests in the subquark superstring as the 840 turns in the 2½ revolutions of the outer half of each whorl and the 840 turns in the 2½ revolutions of its inner half.

Properties of the seven enfolded Type C polygons

When the seven regular polygons of the inner Tree of Life are enfolded in one another, a corner of the triangle coincides with the centre of the hexagon and a corner of the pentagon coincides with the centre of the decagon. All the 31 geometrical elements making up the sector of the hexagon that is replaced by the triangle disappear, so that, instead of 169 geometrical elements (see table above), the hexagon is now left with five sectors containing (169−31=138) elements. 46 yods also disappear from this sector because it is a Type B triangle with 46 yods, so that, instead of 253 yods, the hexagon is left with (253−46=207) yods. Below are tabulated the geometrical and yod compositions of the seven enfolded Type C polygons outside their shared root edge:

Comments

• The seven enfolded polygons have 423 triangles with 227 corners outside the root edge. 227 is the 49th prime number, showing how EL ChAI, the Godname of Yesod with number value 49, prescribes the skeletal shape of the seven enfolded Type C polygons. Including the two endpoints of the shared root edge, the seven enfolded polygons have 229 corners. The Godname ELOHIM with number value 50 prescribes the number of corners because 229 is the 50th prime number. This is a spectacular illustration of the power of Godnames at work in mathematically determining the geometry of the inner Tree of Life.
• The seven enfolded polygons have 650 (=65×10) corners & triangles and 651 sides outside the root edge. This shows how ADONAI, the Godname of Malkuth with number value 65, prescribes the seven enfolded polygons. As the topmost corner of the hexagon coincides with the lowest corner of the hexagon belonging to the seven polygons enfolded in the next higher, overlapping Tree of Life, 1300 geometrical elements outside the root edge are intrinsic to the set of seven polygons enfolded in adjacent Trees of Life, where
  

  		14
  		24	24
  1300 = 15 + 25 + 35 + 45 =	34	34	34
  	44	44	44  44

  This means that 2600 (=26×10×10) geometrical elements are intrinsic to both sets of seven enfolded polygons, where

2600 = 51² − 1 = 3 + 5 + 7 + ... + 101

is the sum of the first 50 odd integers after 1 and 101 (the number value of Michael, the Archangel of Tiphareth) is the 26th prime number. This shows how both ELOHIM with number value 50 and YAHWEH with number value 26 prescribes how many intrinsic geometrical elements are needed to construct the (7+7) enfolded polygons, starting with the root edge. Such beautiful harmony between number and geometry is powerful evidence of the archetypal status of this sacred geometry.

• There are 1529 yods outside the root edge lining the 423 tetractyses in the seven enfolded polygons. Hence, (2×1529 + 4 = 3062) yods line the 846 tetractyses in the (7+7) enfolded polygons. The topmost corners of the two hexagons coincide with the lowest corners of the hexagons enfolded in the next higher Tree. This means that 3060 (=306×10) boundary yods are intrinsic to each set of 14 enfolded polygons. 1530 (=153×10) intrinsic, boundary yods are associated with each set. This shows how ELOHIM SABAOTH, the Godname of Hod with number value 153, prescribes the shape of the inner Tree of Life whose polygons are Type C.
• Outside the root edge are 227 corners of the 423 triangles in the seven enfolded polygons. The dodecagon has 59 such corners of 108 triangles, so that the first six enfolded polygons have 168 such corners of 315 triangles. Both sets of the first six enfolded polygons, which have 50 polygonal corners, have (168+168=336) corners of (315+315=630) triangles outside the root edge, where 630 is the number value of Seraphim, the Order of Angels assigned to Geburah. ELOHIM, the Godname of Binah with number value 50, prescribes the superstring structural parameter 336, which is the number of turns in each of the 50 revolutions of the ten whorls of the UPA about its spin axis. Including the two endpoints of the root edge, the first (6+6) enfolded polygons have 338 corners. But the topmost corners of their two hexagons coincide with the lowest corners of the hexagons enfolded in the next higher Tree of Life. This means that 336 corners are intrinsic to each set of (6+6) enfolded polygons. The number of intrinsic corners of the first (6+6) polygons enfolded in n Trees of Life = 336n. The 120 such polygons enfolded in 10 overlapping Trees have 3360 intrinsic corners. This is the number of turns per revolution in all ten whorls of the UPA. Each revolution of a whorl can be represented by a Tree of Life, so that 50 overlapping Trees represent the 50 revolutions of the whorls of the UPA. The 600 polygons of the first six types enfolded in these Trees have (336×50=16800) intrinsic corners. This is the number of turns in the ten whorls of the UPA. The five sets of 10 Trees making up 50 Trees correspond to the five revolutions of 10 whorls. These Type C polygons provide a geometrical representation of the UPA/subquark superstring because the first six polygons constitute a holistic subset of the complete set of seven polygons, as has been illustrated many times elsewhere in this website. The fact that the first six polygons of the inner Tree of Life have 36 corners when separate and 26 corners when enfolded, both enfolded sets having 50 corners, serves to illustrate how they are prescribed by the Godnames of the ten Sephiroth (see Article 8 for more details).
• The 423 triangles in the seven enfolded polygons have 881 corners & sides. There are five corners & sides on the vertical axis of the hexagon that are shared with the outer Tree of Life as its Pillar of Mercy (they are shown coloured green in the diagram above). Similarly for the hexagon in the other set of polygons, five corners & sides coincide with the Pillar of Judgement. One of these corners is the centre of the hexagon, so that (881−5−6=870=87×10) intrinsic corners & sides surround the centres of the seven enfolded polygons. 87 is the number value of Levanah, the Mundane Chakra of Yesod. 878 corners & sides in each set of seven enfolded polygons are outside the root edge. Of these, five corners & sides are shared with the outer Tree, leaving 873 corners & sides outside the 

 

root edge that are intrinsic to each set. They include the centre of the triangle, one of whose corners is the centre of the hexagon, the centre of the pentagon, one of whose corners is the centre of the decagon, and 31 polygonal corners. Hence, there are (873−2−31=840) intrinsic corners & sides of triangles that are not either corners of polygons or centres of polygons that have corners shared with other polygons. Outside the root edge of both sets of enfolded polygons are (840+840=1680) such intrinsic sides & corners of triangles. Alternatively, each set of seven enfolded polygons has (including the root edge) 881 corners & sides, of which 41 corners are corners of their 47 sectors, leaving 840 corners & sides, so that both separate sets have 1680 such corners & sides other than corners of sectors. Each set separately embodies the superstring structural parameter 840, whilst both sets of enfolded polygons embody the superstring structural parameter 1680. Ten overlapping Trees mapping the 10 whorls of the UPA have an inner form containing 16800 intrinsic corners & sides that are not pure corners of their (70+70) enfolded Type C polygons. This is the inner Tree of Life representation of the subquark state of the E₈×E₈ heterotic superstring.

<< Previous    1...   27  28  [29]  30  31  ...39    Next >>

Home