| << Previous 1... 29 30 [31] 32 33 ...39 Next >> |
#31 Connection between the inner Tree of Life and the outer Tree with Type A triangles

Outer Tree of Life
There are 10 yods inside a Type A triangle. Two hexagonal yods
lie on each of the 22 sides of the 16 triangles with 10 corners that make up the outer Tree of Life. The
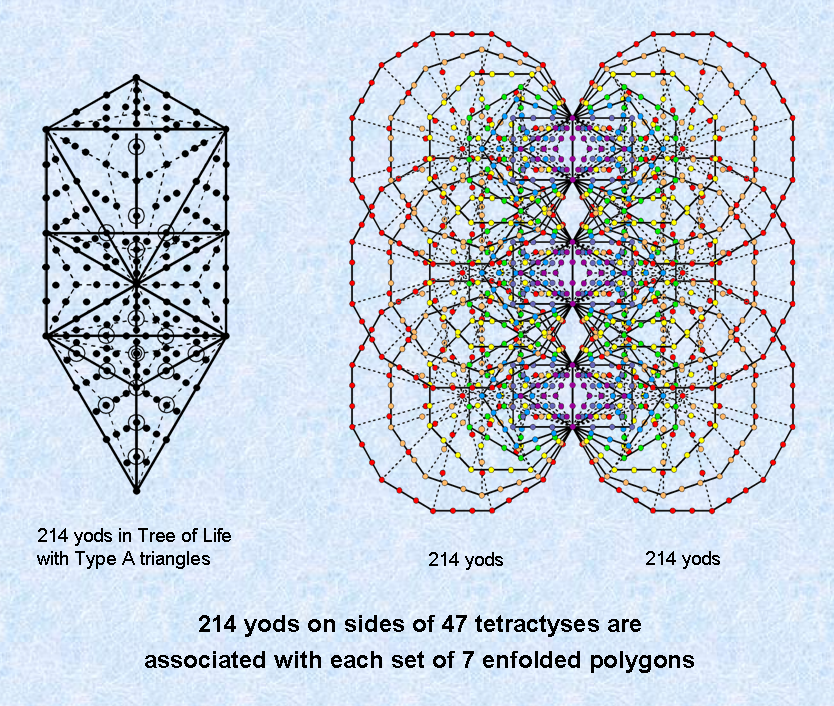
number of yods in the outer Tree composed of Type A triangles = 10 + 22×2 + 16×10 = 214.
48 hexagonal yods are centres of the 48 tetractyses, leaving 166
yods that line their 70 sides. 48 is the number value of Kokab, the Mundane
Chakra of Hod. Of these, 10 yods are corners of the Type A triangles and a further 16 are corners of
tetractyses. Hence, (166−10−16=140) hexagonal yods and (10+16=26) corners
line the 70 sides of the 48 tetractyses. 26 is the number value
of YAHWEH, the Godname of Chokmah, and 140 is the number value of Masloth,
the Mundane Chakra of this Sephirah. It is a remarkable, chance-defying conjunction in the same context of
two number values associated with the same Sephirah and referring to its function in the four
Kabbalistic Worlds. There are (214−26=188) hexagonal yods in the outer Tree of Life. 188 is
the 187th integer after 1, where 187 is the number value of
Auphanim, the Order of Angels assigned to Chokmah.
Inner Tree of Life
Converted into tetractyses, the 47 sectors of the seven enfolded Type A polygons have 264 yods. 47 hexagonal yods are at the centres of tetractyses and (264−47=217) yods line their 88 sides. One of these is the topmost corner of the hexagon, which coincides with the lowest corner of the hexagon enfolded in the next higher, overlapping Tree of Life. The number of yods lining the 47n tetractyses of the 7n polygons enfolded in n overlapping Trees of Life = 216n + 1. The number 216 of Geburah is the number of yods lining tetractyses in the inner form of successive Trees of Life. Two yods in the root edge shared by the pair of sets of seven enfolded polygons can be associated with one set and the other two yods can be associated with the second set. This means that the number of boundary yods associated with the 7n polygons = 214n + 1. Therefore, 214 yods are needed to shape the 47 tetractyses in the seven polygons enfolded in successive Trees.
We see that the yod population of the outer Tree of Life with Type A triangles is equal to the number of yods associated with the inner form of successive Trees that are needed to form the boundaries of its 47 tetractyses. In each case, the number serves the same function of determining its form.
| << Previous 1... 29 30 [31] 32 33 ...39 Next >> |