
Collective Properties of the Seven Polygons of the Inner Tree of Life

A Type A n-gon has (6n+1) yods. The sum of the first (6n+1) integers 1, 2, 3, ... (6n+1) that can be assigned to its yods = ½(6n+1)(6n+2) = (6n+1)(3n+1), so that the arithmetic mean of these integers = 3n + 1. A Type B n-gon has (15n+1) yods. The sum of the integers that can be assigned to its yods = ½(15n+1)(15n+2), so that their arithmetic mean = (15n+2)/2. The arithmetic means are tabulated below for the seven Type A and Type B regular polygons of the inner Tree of Life:
|
triangle |
square |
pentagon |
hexagon |
octagon |
decagon |
dodecagon |
|
| Type A | |||||||
| sum of integers = |
190 |
325 |
496 |
703 |
1225 |
1891 |
2701 |
| arithmetic mean = |
10 |
13 |
16 |
19 |
25 |
31 |
37 |
| Type B | |||||||
| sum of integers = |
1081 |
1891 |
2926 |
4186 |
7381 |
11476 |
16471 |
| arithmetic mean = |
23.5 |
31 |
38.5 |
46 |
61 |
76 |
91 |
For the simplest polygon — the triangle — the average of its 19 integers is 10 (the Pythagorean Decad) when it is Type A. For the Type A decagon, the average of its 61 integers is 31, the number of EL ("God"), the Godname of Chesed, and for the Type B decagon, the average of its 151 integers is 76, the number of YAHWEH ELOHIM, which is the Godname of Tiphareth. The sum of the 46 integers in the Type B triangle is 1081, the number of Tiphareth. The Type B dodecagon embodies the number of Trees in CTOL (see here) because the average of its 181 integers is 91. The Type A pentagon embodies the number 496 of Malkuth as the sum of the first 31 integers that can be assigned to its 31 yods. This polygon therefore embodies the dimension 496 of SO(32) and E8×E8, the two gauge symmetry groups at the heart of superstring theory that were shown in 1984 to be free of quantum anomalies (see here). The decagon is unique in having Godname numbers as the arithmetic mean of its integers for both Type A (31) and Type B (76) versions.
For the seven regular polygons forming each half of the inner Tree of Life, when the first (6n+1) integers are assigned to the yods in a Type A n-gon, there are 295 integers (seven 1's at their centres surrounded by 288 integers), where
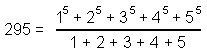
and 288 = 11 + 22 + 33 + 44 = 1!×2!×3!×4!. Their sum = 7531 = 1 + 251×30. This is generated by assigning the integer 1 to the centre of a Type A pentagon and the number 251 to the 30 yods surrounding it, 251 being the number of yods in the 1-tree with Type A triangles as its 19 triangles (see here). The sum of the 151 internal odd integers in the seven Type A polygons = 3841 = 1 + 48×80. This can be generated by assigning 1 to the centre of a Type A octagon and the number 80 to the 48 yods that surround it. 80 is the number of Yesod and the representation comprises 49 integers, where 49 is the number value of EL ChAI, the Godname of Yesod. The sum of the 144 even integers on the sides of the seven polygons = 3690 = 369×10, where
369 = 21 + 26 + 50 + 31 + 36 + 76 + 129
is the sum of the numbers of the Godnames of the first seven Sephiroth.
Collective properties of the sets of seven Type A polygons and seven Type B polygons are listed below:
Type A polygons
(1) Number of corners of the seven polygons = 48
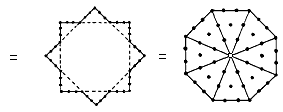
This is the counterpart in its inner form of the 48 corners, lines & triangles making up the outer form of the Tree of Life (see here). 48 is the number of Kokab, the Mundane Chakra of Hod. It is a basic parameter of holistic systems that embody the divine archetypes. It appears in superstring theory as the kernel of the number 480 (=48×10) denoting the number of non-zero roots of the gauge symmetry group E8×E8. Its representation as the 48 yods on the edge of two interlaced squares (24 yods in each one) illustrates how the Pythagorean Tetrad symbolised by the square defines this important structural parameter of the Tree of Life and Tree of Life patterns. This also expresses the (24+24) division of this number that is characteristic of holistic systems, manifesting in one of the two heterotic superstring theories as the direct product of two similar Lie groups E8, each with 240 roots. It manifests in the octagon as the 24 yods on its boundary and the 24 internal yods surrounding its centre. This 24:24 division of the holistic parameter 48 is characteristic of all sacred geometries (see here and here).
(2) Number of corners of 48 tetractyses in the seven polygons = 55
|
1 |
||||
| 2 | 3 | |||
| = |
4 |
5 |
6 |
|
| 7 | 8 | 9 | 10 , |
i.e., it is the tenth triangular number.
(3) Number of yods in the seven polygons = 295. This is the number of SLs up to Chesed of the 49th Tree and the number of yods in a Type A 49-gon. It shows how the number 49 of EL ChAI prescribes the yod population of the seven Type A polygons making up the inner Tree of Life. The heptagonal representation of the number 295 shown below:
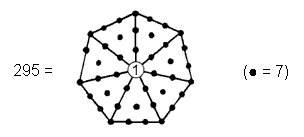 |
|
reveals the seven-fold aspect of its cosmic meaning, for it is the number of SLs up to Chesed (the first of the seven Sephiroth of Construction) of the 49th Tree of Life representing the highest (seventh) subplane of the highest (Adi) plane of the seven planes of consciousness that constitute the cosmic physical plane (see here). The integer 1 at the centre of the heptagon shown above with tetractyses as its sectors denotes the nadir of CTOL. A Type C heptagon has 295 yods:
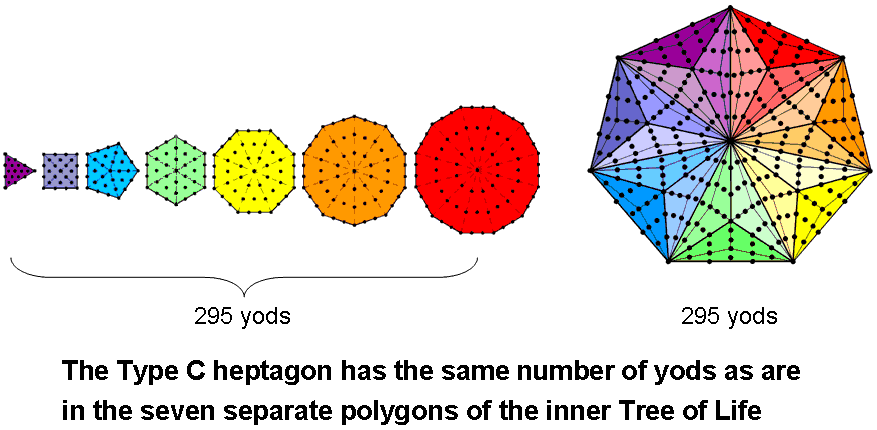
Amazingly, the Type C heptagon with seven corners embodies the very yod population of the seven types of polygons that make up the inner Tree of Life! The mathematical reason for this is simple to see: the number of yods in a Type A n-gon = 6n +1, so that the number of yods in the seven Type A polygons with 48 corners = 6×∑n + 7 = 6×48 + 7 = 6×49 + 1. The sectors of a Type C n-gon are Type B triangles with 46 yods, so that there are 42 yods per sector. The number of yods in the Type C heptagon = 7×42 + 1 = 7×6×7 + 1 = 6×49 + 1, which is the number of yods in the seven Type A polygons, as well as the number of yods in the Type A 49-gon. The 42 yods per sector correspond to the 42 SLs in every seven overlapping Trees of Life, so that the seven sectors of the Type C heptagon map the (1 + 7×42 = 295) SLs up to Chesed of the (7×7=49)th Tree.
(4) Number of yods in the root edge and the seven polygons = 4 + 295 = 299
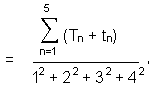
where
|
1n |
4n |
||||||||
| 2n | 2n | 3n | 3n | ||||||
| Tn = |
3n |
3n |
3n |
and tn = |
2n |
2n |
2n |
||
| 4n | 4n | 4n | 4n | 1n | 1n | 1n | 1n . |
This shows
how the Pythagorean integers 1, 2, 3 & 4 express the number of SLs in the 49-tree representing the
cosmic physical plane.
(5) Number of yods in the seven polygons
surrounding their centres = 288
= 11 + 22 + 33 + 44
= 1!×2!×3!×4!
= 23 + 43 + 63
= 172 − 1 = 3 + 5 + 7 +... + 33 (33 = 1! + 2! + 3! + 4!)
|
3 |
11 |
19 |
27 |
3 |
11 |
19 | 27 | |||||
|
5 |
13 |
21 |
29 |
5 | 13 | 21 | 29 | |||||
| = |
7 |
15 |
23 |
31 |
= |
7 | + |
15 |
23 | 31 | ||
|
9 |
17 |
25 |
33 |
9 |
17 |
25 | 33 | |||||
|
= |
|
48 |
|
+ |
240, |
|||||||
where
|
24 |
|||||
| 24 | 24 | ||||
| 240 = |
24 |
24 |
24 |
||
|
24 |
24 | 24 | 24 |
is the number of hexagonal yods in the seven polygons corresponding to Sephiroth of Construction (see here) and 48 is the number of their corners. 240 is the sum of the 24 permutations of the four integers 1, 2, 3 & 4 because (1+2+3+4=10) and 4! = 1×2×3×4 = 24. This number is the sum of the numbers of the Godnames of the first six Sephiroth:
240 = 21 + 26 + 50 + 31 + 36 + 76.
It is also the number of roots of the superstring gauge symmetry group E8 (see here). The expressions of beautiful, arithmetic proportion demonstrate par excellence how the integers 1, 2, 3 & 4 are the natural basis for representing the populations of the various types of yods in the seven tetractys-divided polygons that make up each half of the inner Tree of Life. As displayed above, the square symbolizing the number 4 (Tetrad) determines the number 288 as the sum of a 4×4 square array of the first 16 odd integers after 1 (see also here). It is also the number of yods that surround the centre of a square with 2nd-order tetractyses as its sectors:

(6) Number of yods in the (7+7) polygons surrounding their centres = 576 = 242 = 12×22×32×42 = 1 + 3 + 5 +... + 47, where 36 is the Godname number of Geburah and 47 (= 21 + 26) is the 24th odd integer (24=4!) and the number of SLs in the 7-tree. It is remarkable that the population of non-central yods in both sets of polygons is determined by this parameter of the 7-tree (the Theosophical "physical plane," or physical universe). The Godname YAH with number value 15 prescribes its SL population because 47 is the 15th prime number. As 576 = 288×2, this number is the number of yods that surround the centre of an octagon with 2nd-order tetractyses as sectors (there are 72 yods per sector and 576 = 8×72; see here).
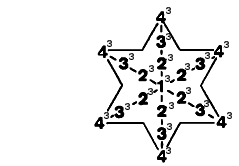
(7) Number of yods in the (7+7) polygons & root edge = 594. This is the sum of the cubes of 2, 3 & 4 surrounding the central cube of 1 in the Star of David array:
(8) Number of yods lining sides of the 48 tetractyses in the seven polygons =
247

The sum (7) of the seven binomial coefficients forming the right-sloping side of this Pascal's Triangle array of the first 28 binomial coefficients is the number of centres of the polygons. The sum (240) of the remaining 21 coefficients is 240, which is both the number of hexagonal yods in the seven polygons and the number of yods other than centres that line sides of the 48 tetractyses.
(9) Number of yods lining sides of the (48+48) tetractyses in the (7+7) polygons = 494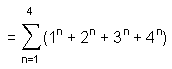
11
12 13 14
=21
22 23 24 31
32 33 34 41
42 43 44 .
This is a remarkable example of the power of the Pythagorean integers 1, 2, 3 & 4 to represent properties of holistic systems. 494 is also the sum of the 295 integers 1, 2, 3 & 4 forming the tetractys sectors of the 49-sided polygon:
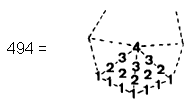
This representation shows how the mathematical archetype
embodied in the Godname EL ChAI of Yesod prescribes through 1, 2, 3 & 4 the population of yods on sides
of the tetractys sectors of both sets of polygons. There are 494 yods other than their corners, so we need 494
more yods to create the polygons of the inner Tree of Life from tetractyses.
(10) Number of yods on boundaries of the seven polygons = 144
| = |
10 |
20 | 30 | 40 |
|
11 |
21 | 31 | 41 | |
|
12 |
22 | 32 | 42 | |
|
13 |
23 | 33 | 43. |
144 (= 122) is the 12th Fibonacci number and the only Fibonacci number that is the square of an integer. 144 is also the number of yods other than centres inside the seven polygons.
Number of yods on the boundaries of the (7+7) polygons = 288 (see (5). This is also the number of yods other than centres inside both sets of polygons.
(12) Number of yods in the root edge and on the boundaries of the seven polygons = 148, the number of Netzach, the fourth Sephirah from Malkuth.
(13) Number of yods in the root edge and on the boundaries of the (7+7) polygons = 4 + 288 = 292
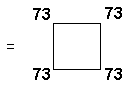
where 73 is the
21st prime number and the gematria number value of Chokmah ("Wisdom").
(14) Number of boundary yods & centres of the seven polygons = 144 + 7 = 151.
This is the 76th odd integer, where 76 is the number value of YAHWEH ELOHIM, the
Godname of Tiphareth.
(15) Number of
yods in the root edge and inside the seven polygons = 155. This is also the number of yods in the root edge,
at the centres of the polygons and on their boundaries. In keeping with the meaning of Malkuth, the number of
ADONAI MELEKH, the Godname of this Sephirah, determines those yods that create the outer form of the
polygons.
The seven separate Type A polygons consist of 55 corners, where 55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10, and 96 sides of 48 triangles, i.e., they comprise 199 geometrical elements. This number is the 100th odd integer, where 100 = 102, showing how the Decad determines the geometrical composition of the inner Tree of Life. 192 geometrical elements surround the centres of the seven polygons. Both sets of polygons comprise 110 corners and 192 sides of 96 triangles, i.e., 398 geometrical elements. The number 110 = 10×11, where 11 is the 10th integer after 1, showing again how the Decad determines the geometrical composition of the inner Tree of Life. 384 geometrical elements surround the centres of the 14 Type A polygons. This number is a parameter of all holistic systems (see here). The 384 geometrical elements comprise 192 corners & triangles and 192 sides. This 192:192 division of the holistic parameter 384 is characteristic of holistic systems (see here). It also has a musical counterpart (see here).
(16) The (7+7) enfolded Type A polygons have 524 yods, of which 80 yods are corners of the (47+47) tetractys sectors of the polygons and 444 yods are hexagonal yods. A Type C polygon with n corners has 42n yods surrounding its centre. Of these 5n yods are corners of tetractyses and 37n yods are hexagonal yods. A Type C dodecagon (n=12) comprises 108 tetractyses with 60 black corners and 444 red hexagonal yods:
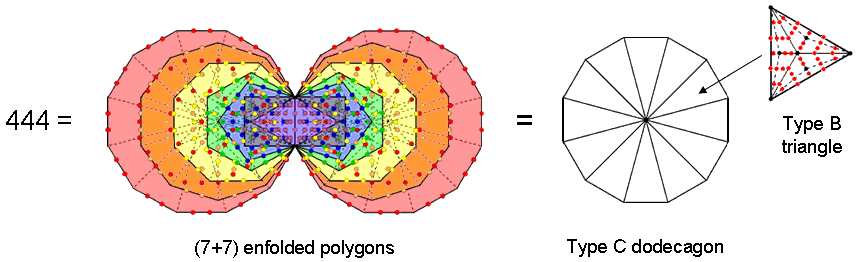
The fact that the Type C dodecagon contains as many hexagonal yods as the inner Tree of Life is striking evidence of the holistic nature of the dodecagon, as confirmed in many places in this website. It is the single, polygonal version of the inner Tree of Life.
Type B
polygons
(1) Number of yods in the seven separate Type B
polygons = 727, which is the 129th prime number. In this remarkable way, the Godname number of the
generative Sephirah Netzach, the seventh Sephirah from the top of the Tree of Life, determines the
population of the seven Type B polygons.
(2) Number of yods in the (7+7) Type B polygons = 2×727

The number of integers in this representation = 41 = 26 + 15, i.e., the sum of the numbers of the two Godnames of Chokmah, namely, YAH and YAHWEH.
(3) Two yods of the root edge are associated with each set of polygons. Number of yods in the seven Type B polygons + ½ root edge = 2 + 727 = 729 = 272 = 36 = 93. The number of yods associated with each set of Type B polygons is the cube of 9, the fourth odd integer after 1. This illustrates once more the role of the Pythagorean Tetrad in determining the properties of the inner form of the Tree of Life.
(4) Number
of yods in the seven Type B polygons & root edge = 727 + 4
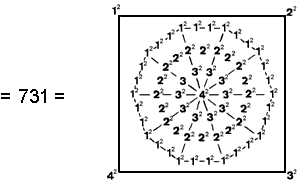
This tetractys-divided decagon with 65 squares of 1, 2, 3 & 4 is the representation of the number of ADONAI (see here). It is remarkable that, when the squares of the integers 1, 2, 3 & 4 are assigned to its yods, their sum is the number of yods in the seven Type B polygons and the separate root edge. This is an example of the potent, mathematical archetype of the Godname of Malkuth expressing through its geometrical representation the yod population of the set of Type B polygons and the root edge.
(5) Number of yods in (7+7) polygons & root edge = 4 + 2×727 = 1458.
(6) Number of yods in the seven Type B polygons surrounding their centres = 727 − 7 = 720 =
1×2×3×4×5×6
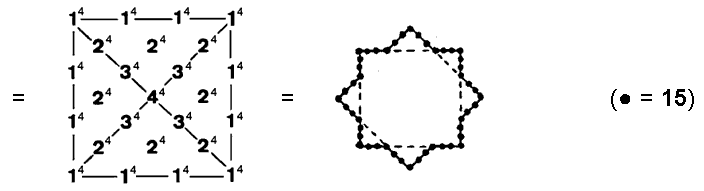
This demonstrates the way in which the Tetrad symbolized by the square expresses yod populations of the seven polygons. We saw in the discussion of the seven Type A polygons that they have as many yods surrounding their centres as a square with 2nd-order tetractyses as its sectors has yods surrounding its centre. Another way in which the Tetrad determines the number 720 is as follows: the fourth triangular number is 10, the Decad. This is symbolized by the ten-cornered decagon, which has 720 yods surrounding its centre when its sectors are 2nd-order tetractyses:
| 720 = | 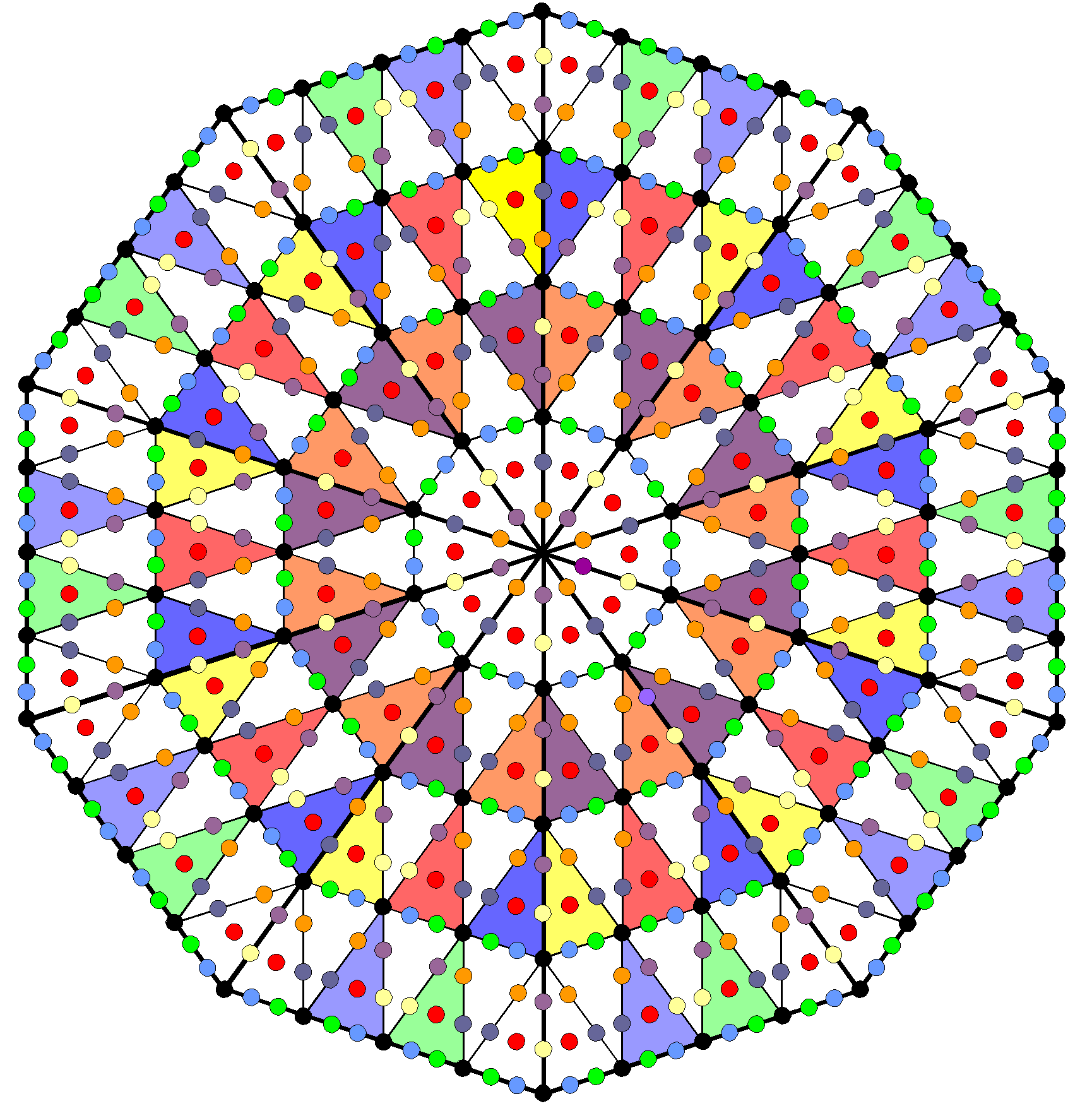 |
The yod population of the inner form of the ten-fold Tree of Life is embodied, appropriately, in this geometrical symbol for the number 10.
(7) Number of yods surrounding the centres of the (7+7) Type B polygons = 2×720
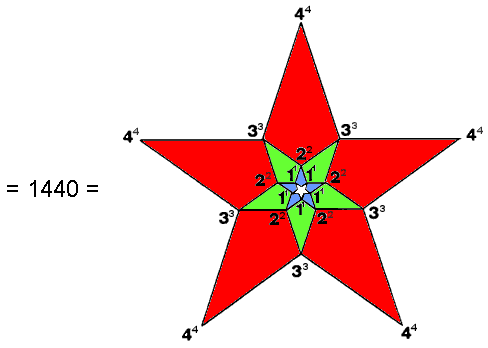
(8) Number of non-central yods
in the (7+7) Type B polygons & root edge = 1440 + 4
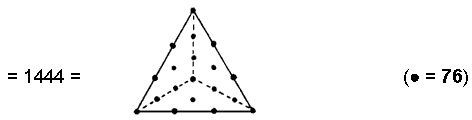
This is the number of yods in 76 Type A triangles, illustrating how
the mathematical archetype in YAHWEH ELOHIM prescribes this number. The 65-tree has 1444 corners &
edges of triangles. The Type B division of the (7+7) polygons therefore encodes
the minimum number of geometrical elements needed to construct the section of CTOL prescribed by the
Godname ADONAI of Malkuth. Curiously, the 65-tree has 133 SLs on its central pillar, where 133 is the
dimension of E7, the largest, exceptional subgroup of E8, the rank 8, exceptional Lie group.
The number of non-central yods in the (7+7) Type A polygons & root edge = 288 + 288 + 4
= 580. The extra number of yods in the seven Type B polygons = 1444 − 580 = 864

(9) Number of hexagonal yods in the seven Type B polygons = 624
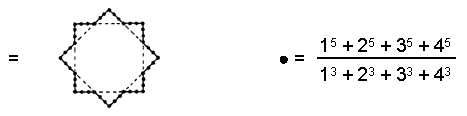
= 25 2 − 1 = 3 + 5 + 7 +… + 49,
i.e., 624 is the sum of the 24 (= 1×2×3×4) odd integers after 1 up to 49, the Godname number of Yesod, showing how EL ChAI prescribes the number of yods in the seven polygons that are not corners.
(10) Number of hexagonal yods in the (7+7) Type B polygons = 2×624
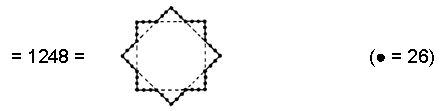
Compare this with property (6). The two Godname numbers 15 & 26 of Chokmah determine in similar fashion the population of non-central yods in the seven polygons and the population of hexagonal yods in the (7+7) polygons.
(11) The
root edge has two hexagonal yods. Number of hexagonal yods in the (7+7) polygons & root edge = 1248 +
2
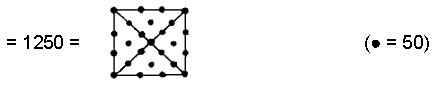
This shows how the formative archetype of ELOHIM with number value 50 expresses through the
square — the symbol of the Tetrad — the population of hexagonal yods that symbolise the seven Sephiroth of
Construction.
(12) Number of corners of tetractyses in the seven Type B polygons = 103, which is the number of SABAOTH (“Hosts”), part of the Godnames assigned to Netzach and Hod.
(13) Number of internal yods in the seven Type B polygons = 583
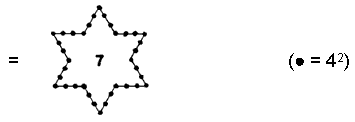
(the central integer ‘7’ denotes the number of their centres).
(14) Number of yods inside the seven Type B polygons other than their centres = 583 − 7 = 576 = 12×22×32×42. This illustrates par excellence the basic role of the Pythagorean Tetrad and the integers 1, 2, 3 & 4 in expressing properties of the inner form of the Tree of Life. There are 576 yods surrounding the centres of the (7+7) Type A polygons (see (6) in the discussion of Type A polygons).
The seven Type B polygons consist of 103 corners & 240 sides of 144 triangles, i.e., 487 geometrical elements, where 103 is the number value of SABAOTH ("Hosts"), part of the Godnames of Netzach and Hod. Including the root edge, which comprises two endpoints and the straight line joining them, makes a total of 490 (=49×10) geometrical elements. This shows how EL ChAI, the Godname of Yesod with number value 49, prescribes the geometry of the root edge and the seven separate Type B polygons. Surrounding their seven centres are 96 corners & 240 sides of 144 triangles, i.e., 480 geometrical elements made up of 240 corners & triangles and 240 sides. This 240:240 division is the geometrical counterpart of the 480 roots of E8×E8, which are compounded from the 240 roots of each Lie group E8 (see here under "Superstring gauge symmetry group").
Here is remarkable evidence that the inner Tree of Life has properties that are analogous to the root composition of E8×E8, one of the two gauge symmetry groups describing the unified force between heterotic superstrings. Moreover, the seven Type B polygons have 336 corners & sides surrounding their centres, as well as 384 sides & triangles:
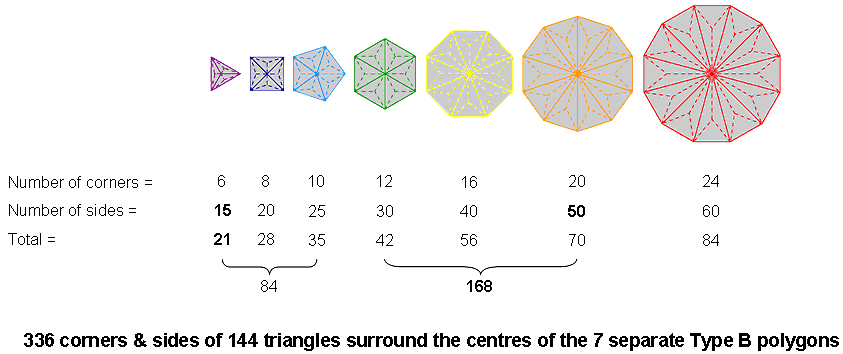
Both these numbers are parameters of holistic systems, e.g., we saw earlier that 384 corners, sides & triangles surround the centres of the 14 separate Type A polygons and that the table of 64 hexagrams forming the basis of the I Ching system of divination comprises 384 lines & broken lines (see here for these and other examples), whilst 336 is a structural parameter of the UPA remote-viewed by Besant & Leadbeater, being the number of circularly polarized oscillations made in a single revolution around its spin axis of each of its ten whorls, encodings of which in sacred geometries are discussed in the section Superstrings as sacred geometry. Notice that the (84+84=168) corners & sides in the triangle, square, pentagon & dodecagon and the 168 corners & sides in the hexagon, octagon & decagon reproduces the 168:168 division of 336 always displayed by sacred geometries. For more examples of these holistic parameters, see The holistic pattern. We find, therefore, that the geometry of the seven Type B polygons embodies both the group-theoretical parameters of E8 and E8×E8 and the structural parameter of the basic unit of matter that Besant & Leadbeater described paranormally 120 years ago and which the author identified over 18 years ago in his book "ESP of Quarks & Superstrings" as the spin-½ subquark state of the E8×E8 heterotic superstring. Anyone who believes that this triple connection might be merely a coincidence also believes in miracles!
General formulae for the geometrical & yod population of any polygon
The concept of nth-order polygons was introduced on #45 in Sacred geometry/Tree of Life. A 1st-order triangle is an ordinary triangle (not necessarily equilateral or isosceles) that is divided into its three sectors; it is what has been called a "Type A triangle". A 2nd-order triangle ("Type B triangle") is a triangle whose sectors are 1st-order triangles; a 3rd-order triangle ("Type C triangle") is a triangle whose sectors are 2nd-order triangles:
|
|
|
|
|
|
0th-order triangle |
1st-order triangle (Type A) |
2nd-order triangle (Type B) |
3rd-order triangle (Type C) |
In general, an nth-order triangle is one whose sectors are (n−1)th-order triangles and an nth-order polygon is an N-gon whose N sectors are (n−1)th-order triangles (n≥1). Table 1 lists formulae for the numbers of corners, sides & triangles in an nth-order N-gon and the number of yods when each 0th-order triangle is turned into a tetractys:
Table 1. Geometrical & yod compositions of the nth-order N-gon.
|
nth-order N-gon |
n = 1 | n = 2 | n = 3 | |
| Number of corners, including centre (cnN) |
½(3n−1+1)N + 1 |
N + 1 | 2N + 1 | 5N + 1 |
| Number of sides (snN) |
½(3n+1)N |
2N | 5N | 14N |
| Number of triangles (tnN) |
3n−1N |
N |
3N |
9N |
| Total number of geometrical elements (gnN) |
cnN + snN + tnN = (3n+1)N + 1 |
4N + 1 |
10N + 1 |
28N + 1 |
| Number of hexagonal yods (hnN) |
2snN + tnN = (4×3n−1 + 1)N |
5N |
13n |
37N |
| Total number of yods (ynN) |
cnN + hnN = (3/2)(3n+1)N + 1 |
6N + 1 |
15n + 1 |
42N + 1 |
("1" denotes the centre of the nth-order N-gon).
General formulae for the geometrical & yod populations of the 7 enfolded polygons and the (7+7) enfolded polygons
Table 2 lists formulae for the geometrical & yod composition of the seven enfolded nth-order polygons and the (7+7) enfolded nth-order polygons that make up the inner Tree of Life:
Table 2. Geometrical & yod compositions of the 7 enfolded nth-order polygons and the (7+7) enfolded nth-order polygons.
|
7 enfolded polygons |
(7+7) enfolded polygons |
|
| Number of corners (including centres of polygons) |
Cn = ½(35 + 47×3n−1) |
2Cn −2 = 33 + 47×3n−1 |
| Number of sides |
Sn = ½(35 + 47×3n) |
2Sn − 1 = 34 + 47×3n |
| Number of triangles |
Tn = 47×3n−1 |
2Tn = 94×3n−1 |
| Total number of geometrical elements |
Gn = Cn + Sn + Tn = 35 + 47×3n |
2Gn − 3 = 67 + 94×3n |
| Number of hexagonal yods |
Hn = 35 + 188×3n−1 |
2Hn − 2 = 68 + 376×3n−1 |
| Total number of yods |
Yn = ½(105 + 47×3n+1) |
2Yn − 4 = 101 + 47×3n+1 |
Let us call the seven enfolded nth-order polygons Pn. Table 2 indicates that the number of corners in Pn ≡ Cn = ½(35 + 47×3n−1). Therefore, the number of corners in Pn+1 = ½(35 + 47×3n). But, according to Table 2, this is the number of sides in Pn. We see that the number of corners in a given Pn is equal to the number of sides in Pn−1, whilst its number of sides is equal to the number of corners in Pn+1.
The number of corners & triangles in Pn = Cn + Tn = ½(35 + 47×3n). According to Table 2, this is equal to the number of sides (Sn). This means that the number (Gn) of corners, sides & triangles in Pn is twice its number of sides: Gn = 2Sn. This property has its counterpart in a polygon of any order, namely, the number of corners & triangles surrounding its centre is twice the number of their sides.* For the (7+7) enfolded polygons, the number of corners & triangles = 33 + 47×3n, which is equal to the number of sides outside the root edge, whatever the order of polygon. These remarkable properties are clearly illustrated in Table 3, which lists the geometrical and yod composition of the inner Tree of Life for n = 1, 2, 3 & 4:
Table 3
|
7 enfolded polygons |
(7+7) enfolded polygons |
|||||||
|
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 1 |
n = 2 |
n = 3 |
n = 4 |
|
| Number of corners (including centres of polygons) | 41 | 88 | 229 | 652 | 80 | 174 | 456 | 1302 |
| Number of sides | 88 | 229 | 652 | 1921 | 175 | 457 | 1303 | 3841 |
| Number of triangles | 47 | 141 | 423 | 1269 | 94 | 282 | 846 | 2538 |
| Total number of geometrical elements | 176 | 458 | 1304 | 3842 | 349 | 913 | 2605 | 7681 |
| Number of hexagonal yods | 223 | 599 | 1727 | 5111 | 444 | 1196 | 3452 | 10220 |
| Total number of yods | 264 | 687 | 1956 | 5763 | 524 | 1370 | 3908 | 11522 |
In the case of the seven enfolded polygons, for n = 1, 41 + 47 = 88; for n = 2, 88 + 141 = 229; for n = 3, 229 + 423 = 652; for n = 4, 652 + 1269 = 1921. In the case of the (7+7) enfolded polygons, for n = 1, 80 + 94 = 175 − 1; for n = 2, 174 + 282 = 457 − 1; for n = 3, 456 + 846 = 1303 − 1; for n = 4, 1302 + 2538 = 3841 − 1.
The number of yods in Pn with Cn corners and Sn sides of Tn triangles ≡ Yn = Cn + 2Sn + Tn. As, according to Table 2, Cn + Tn = Sn, Yn = 3Sn. The number of corners, sides & triangles in Pn = Gn = Cn + Sn + Tn = 2Sn. Therefore, Yn/Gn = 3/2. What is familiar to musicians as the tone ratio 3/2 of the perfect fifth (namely, the arithmetic mean of the tone ratios of the first and last notes of an octave) is the ratio of the yod and geometrical populations of the seven enfolded polygons, whatever their order. This is a remarkable property.
1300 = 15 + 25 + 35 + 45 = |
 |
|
|
|
The number of corners of the 1269 triangles in the seven enfolded 4th-order polygons is 652. Hence, 650 (=65×10) corners are outside their root edge. This is how ADONAI, the Godname of Malkuth with number value 65, prescribes the shape of the inner Tree of Life marked out by its corners. Outside the root edge of the (7+7) enfolded 4th-order polygons are 1300 corners, where
| 14 | ||||
|
24 |
24 |
|||
|
1300 = 15 + 25 + 35 + 45 = |
34 |
34 | 34 | |
|
44 |
44 |
44 |
44 |
This beautiful property, which is expressed by the integers 1, 2, 3 & 4 symbolised by the four rows of the Pythagorean tetractys, reappears in the (7+7) enfolded 2nd-order polygons as the extra 1300 yods needed to construct these polygons marked out by the 80 corners of their 0th-order triangular sectors.
Outside the root edge of the (7+7) enfolded 4th-order polygons are 3840 (=384×10) sides of 2538 triangles; 1920 (=192×10) sides belong to each set of seven enfolded polygons. The number 384 is a defining parameter of holistic systems, which characteristically display in their two "halves" the division: 384 = 192 + 192 (see The holistic pattern). Here is evidence par excellence for the holistic nature of the geometrical object consisting of these enfolded polygons that the author claims is associated with the Kabbalistic Tree of Life as its inner form (see also #54 in Wonders of superstrings).
* Proof: According to Table 1, for an N-gon, the number of corners surrounding its centre = ½(3n−1+1)N, the number of triangles = 3n−1N, and the number of sides = ½(3n+1)N. Therefore, the number of corners & triangles surrounding its centre = ½(3n−1+1)N + 3n−1N = ½(3n+1)N. This is equal to the number of sides.