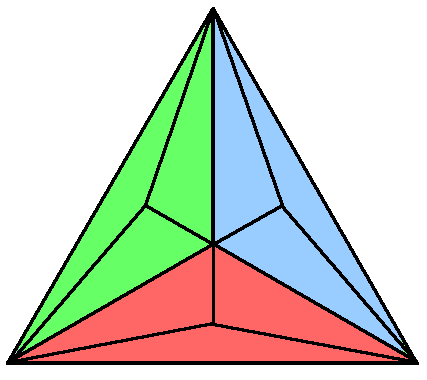
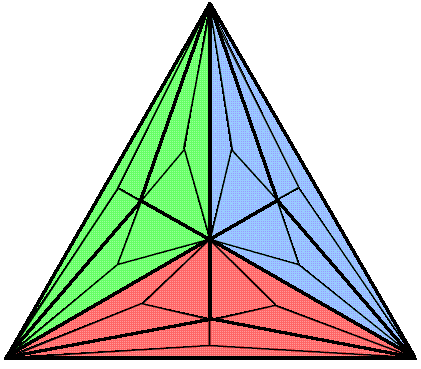
0th-order triangle
1st-order triangle (Type A)
2nd-order triangle (Type B)
3rd-order triangle (Type C)
4th-order triangle (Type D)
| << Previous 1... 41 42 43 44 [45] Next >> |
Formulae for the geometrical and yod compositions of the outer & inner
forms of n Trees of Life/n-tree composed of any order of triangle or polygon
As explained in #8, the triangles that are the basic building blocks of sacred geometry can be considered not only as pure triangles (what we may call "0th-order triangles") but also as triangles divided into their three sectors ("Type A triangles," called here "1st-order triangles"). If each sector of the Type A triangle is then divided into its three sectors, it becomes a "Type B triangle," or a "2nd-order triangle." It is composed of (32=9) 0th-order triangles. The next division into three sectors of each 0th-order triangle in a Type B triangles generates a "Type C triangle" ("3rd-order triangle") with (33=27) 0th-order triangles, and so on. An nth-order triangle is the result of n successive divisions of a 0th-order triangle into 3n 0th-order triangles:
 |
 |
 |
 |
 |
|
0th-order triangle |
1st-order triangle (Type A) |
2nd-order triangle (Type B) |
3rd-order triangle (Type C) |
4th-order triangle (Type D) |
Table 1 shows how the numbers of corners, sides & triangles inside the parent triangle increase with n:
Table 1
|
|
n = 0 | n = 1 | n = 2 | n = 3 | n = n |
| Number of corners (c) | 0 | 30 | 30 + 31 | 30 + 31 + 32 | 30 + 31 + 32 +...+ 3n−1 = ½(3n−1) |
| Number of sides (s) | 0 | 31 | 31 + 32 | 31 + 32 + 33 | 31 + 32 + 33 +...+ 3n = (3/2)(3n−1) |
| Number of 0th-order triangles (t) | 30 | 31 | 32 | 33 | 3n |
| Number of geometrical elements (g=c+s+t) | 1 | 7 | 25 | 79 | 3n+1 − 2 |
Geometrical composition
The numbers of corners, sides & 0th-order triangles in N Trees
of Life or in the N-tree are listed in Table 2:
Table 2
| N Trees of Life |
N-tree |
|
| Number of corners (C) | 6N + 4 | 6N + 5 |
| Number of sides (S) | 16N + 6 | 16N + 9 |
| Number of triangles (T) | 12N + 4 | 12N + 7 |
| Number of geometrical elements (G) | 34N + 14 | 34N + 21 |
The number of corners of the Tt triangles in N Trees/N-tree with T nth-order triangles ≡ C = C + Tc.
The number of sides of the Tt triangles in N Trees/N-tree ≡ S = S + Ts.
The number of 0th-order triangles in N Trees/N-tree ≡ T = Tt.
The number of geometrical elements in N Trees/N-tree ≡ G = C + S + T = C + S + T(c+s+t) = C + S + Tg.
Table 3 lists the calculated geometrical composition of N Trees/N-tree with nth-order triangles:
Table 3
|
N Trees of Life |
N-tree |
|
| Number of corners (C) | 2 + 2(3N+1)3n |
½[3 + (12N+7)3n] |
| Number of sides (S) |
−2N + 2(3N+1)3n+1 |
½[−(4N+3) + (12N+7)3n+1] |
| Number of triangles (T) | 4(3N+1)3n |
(12N+7)3n |
| Number of geometrical elements (G) | 2 − 2N + 4(3N+1)3n+1 |
−2N + (12N+7)3n+1 |
The cases N = 1 and N =10 are of special interest because 10 overlapping Trees of Life are an expanded version of the single Tree of Life. Table 4 lists their geometrical compositions for 0th- & 1st-order triangles:
Table 4
|
N Trees of Life |
N-tree | |||||||
|
Corners |
Sides |
Triangles |
Total |
Corners |
Sides |
Triangles |
Total |
|
|
n = 0 (all triangles are tetractyses) |
||||||||
| N = 1 | 10 | 22 | 16 | 48 | 11 | 25 | 19 | 55 |
| N = 10 |
64 |
166 | 124 | 354 | 65 | 169 | 127 | 361 |
|
n = 1 (all triangles are Type A) |
||||||||
| N = 1 | 26 | 70 | 48 | 144 | 30 | 82 | 57 | 169 |
| N = 10 | 188 | 538 | 372 | 1098 | 192 | 550 | 381 | 1123 |
Table 5 lists the geometrical composition of N Trees/N-tree for the cases n = 0, 1, 2, & 3:
Table 5
|
N Trees of Life |
N-tree | |||||||
|
n |
Corners |
Sides |
Triangles |
Total |
Corners |
Sides |
Triangles |
Total |
|
0 |
6N + 4 | 16N + 6 | 12N + 4 | 34N + 14 | 6N + 5 | 16N + 9 | 12N + 7 | 34N + 21 |
| 1 | 18N + 8 | 52N + 18 | 36N + 12 | 106N + 38 | 18N + 12 | 52N + 30 | 36N + 21 | 106N + 63 |
|
2 |
54N + 20 | 160N + 54 | 108N + 36 | 322N + 110 | 54N + 33 | 160N + 93 | 108N + 63 | 322N + 189 |
|
3 |
162N + 56 | 484N + 162 | 324N + 108 | 970N + 326 | 162N + 96 | 484N + 282 | 324N + 189 | 970N + 567 |
Yod composition
The number of hexagonal yods inside each of the T nth-order triangles = 2s +
t.
The number of hexagonal yods lining the outer sides of these nth-order triangles = 2S.
The number of hexagonal yods in N Trees/N-tree ≡ H = 2S + T(2s+t).
The number of yods in N Trees/N-tree ≡ Y = C + 2S + T(2s+t).
Table 6 lists the yod population of N Trees/N-tree with nth-order triangles:
Table 6. Yod population of N-trees/N-tree with nth-order triangles.
|
|
N Trees of Life |
N-tree |
| Number of corners (C) | 2 + 2(3N+1)3n | ½[3 + (12N+7)3n] |
| Number of hexagonal yods (H) | −4N + 16(3N+1)3n | −(4N+3) + 4(12N+7)3n |
| Number of yods (Y) | 2 − 4N + 2(3N+1)3n+2 | ½[−(8N+3) + (12N+7)3n+2] |
Table 7 lists the yod populations (Y) for N Trees/N-tree in the case of n = 0 (tetractys), n = 1 (Type A triangle), n = 2 (Type B triangle) & n = 3 (Type C triangle):
Table 7. Yod populations of N Trees/N-tree for n = 0, 1, 2 & 3.
|
n |
N Trees of Life |
N-tree |
|
0 |
50N + 20 | 50N + 30 |
|
1 |
158N + 56 | 158N + 93 |
|
2 |
482N + 164 | 482N + 282 |
|
3 |
1454N + 488 | 1454N + 849 |
The General view section of Power of the polygons discusses the geometrical and yod populations of nth-order polygons (these are polygons whose sectors are (n−1)th-order triangles, where n≥1). Table 8 lists the populations of nth-order N-gons in the general case and for n = 1, 2 & 3:
Table 8. Geometrical & yod compositions of the nth-order N-gon.
|
nth-order N-gon |
n = 1 | n = 2 | n = 3 | |
| Number of corners, including centre (cnN) |
½(3n−1+1)N + 1 |
N + 1 | 2N + 1 | 5N + 1 |
| Number of sides (snN) |
½(3n+1)N |
2N | 5N | 14N |
| Number of triangles (tnN) |
3n−1N |
N |
3N |
9N |
| Number of geometrical elements (gnN) |
cnN + snN + tnN = (3n+1)N + 1 |
4N + 1 |
10N + 1 |
28N + 1 |
| Number of hexagonal yods (hnN) |
2snN + tnN = (4×3n−1 + 1)N |
5N |
13N |
37N |
| Number of yods (ynN) |
cnN + hnN = (3/2)(3n+1)N + 1 |
6N + 1 |
15N + 1 |
42N + 1 |
("1" denotes the centre of the nth-order N-gon).
Table 9 lists the geometrical and yod compositions of the inner form of the Tree of Life:
Table 9. Geometrical & yod compositions of the 7 enfolded nth-order polygons and the (7+7) enfolded nth-order polygons.
|
7 enfolded polygons |
(7+7) enfolded polygons |
|
| Number of corners (including centres of polygons) |
Cn = ½(35 + 47×3n−1) |
C = 2Cn −2 = 33 + 47×3n−1 |
| Number of sides |
Sn = ½(35 + 47×3n) |
S = 2Sn − 1 = 34 + 47×3n |
| Number of triangles |
Tn = 47×3n−1 |
T = 2Tn = 94×3n−1 |
| Number of geometrical elements |
Gn = Cn + Sn + Tn = 35 + 47×3n |
G = C + S + T = 2Gn − 3 = 67 + 94×3n |
| Number of hexagonal yods |
Hn = 35 + 188×3n−1 |
H = 2Hn − 2 = 68 + 376×3n−1 |
| Number of yods |
Yn = ½(105 + 47×3n+1) |
Y = 2Yn − 4 = 101 + 47×3n+1 |
Notice that the number 101 is the 26th prime number and that the number 47, which is the number of sectors of the seven enfolded polygons, is the 15th prime number. The number 26 of YAHWEH, the complete Godname of Chokmah, and the number 15 of YAH, the shorter form of this Divine Name, arithmetically determine the yod population of the inner Tree of Life, whatever the order of its 14 polygons. Notice also that the number 67 of Binah appears in the formula for the geometrical population of the inner Tree of Life. As was revealed in #41, it is the number of yods below Binah of the 1-tree when its 19 triangles are 1st-order triangles.
Let us call the seven enfolded nth-order polygons Pn. Table 9 indicates that the number of corners in Pn ≡ Cn = ½(35 + 47×3n−1). Therefore, the number of corners in Pn+1 = Cn+1 = ½(35 + 47×3n). But, according to Table 9, this is the number of sides (Sn) in Pn. We find that the number of corners in a given Pn is equal to the number of sides in Pn−1, or conversely, that its number of sides is equal to the number of corners (Cn+1) in Pn+1:
Cn+1 = Sn.
The number of yods in Pn outside the shared root edge = ½(105 + 47×3n+1) − 4 = ½(97 + 47×3n+1). The number of Haniel, the Archangel of Netzach, is 97.
The number of corners & triangles in Pn = ½(35 + 47×3n). According to Table 9, this is equal to the number of sides (Sn). This means that the number (Gn) of corners, sides & triangles in Pn is twice its number of sides:
Gn = 2Sn,
so that
Gn = 2Cn+1.
The property Gn = 2Sn has its counterpart in a polygon of any order, namely, the number of corners, sides & triangles surrounding its centre is twice the number of their sides.* For the (7+7) enfolded polygons, the number of corners & triangles = 33 + 47×3n, which is equal to the number of sides outside the root edge, whatever the order of polygon. These remarkable properties are clearly displayed in Table 10, which lists the geometrical and yod composition of the inner Tree of Life for n = 1, 2, 3 & 4:
Table 10
|
7 enfolded polygons |
(7+7) enfolded polygons |
|||||||
|
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 1 |
n = 2 |
n = 3 |
n = 4 |
|
| Number of corners (including centres of polygons) | 41 | 88 | 229 | 652 | 80 | 174 | 456 | 1302 |
| Number of sides | 88 | 229 | 652 | 1921 | 175 | 457 | 1303 | 3841 |
| Number of triangles | 47 | 141 | 423 | 1269 | 94 | 282 | 846 | 2538 |
| Number of geometrical elements | 176 | 458 | 1304 | 3842 | 349 | 913 | 2605 | 7681 |
| Number of hexagonal yods | 223 | 599 | 1727 | 5111 | 444 | 1196 | 3452 | 10220 |
| Number of yods | 264 | 687 | 1956 | 5763 | 524 | 1370 | 3908 | 11522 |
In the case of the seven enfolded polygons, for n = 1, 41 + 47 = 88; for n = 2, 88 + 141 = 229; for n = 3, 229 + 423 = 652; for n = 4, 652 + 1269 = 1921. In the case of the (7+7) enfolded polygons, for n = 1, 80 + 94 = 175 − 1; for n = 2, 174 + 282 = 457 − 1; for n = 3, 456 + 846 = 1303 − 1; for n = 4, 1302 + 2538 = 3841 − 1. Notice that the numbers of geometrical elements for the seven enfolded polygons (green cells) is always twice the number of sides (blue cells).
The number of yods in Pn with Cn corners and Sn sides of Tn triangles ≡ Yn = Cn + 2Sn + Tn. As, according to Table 9,
Cn + Tn = Sn,
Yn = 3Sn.
The number of corners, sides & triangles in Pn ≡ Gn = Cn + Sn + Tn = 2Sn. Therefore,
Yn/Gn = 3/2.
The numbers in Table 10 confirm this for n = 1, 2, 3 & 4:
Yn/Gn = 3/2
264/176 = 687/458 = 1956/1304 = 5763/3842 = 3/2.
Yn = 3Sn
264 = 3×88, 687 = 3×229, 1956 = 3×652, 5763 = 3×1921.
Gn = 2Sn
176 = 2×88, 458 = 2×229, 1304 = 2×652, 3842 = 2×1921.
What is familiar to musicians as the tone ratio 3/2 of the perfect fifth (namely, the arithmetic mean of the tone ratios of the first and last notes of an octave — see here) is also the ratio of the yod and geometrical populations of the seven enfolded polygons, whatever their order. This is a remarkable property. The 0th-order triangle and the tetractys that corresponds to it have an analogous property, for nine yods line its boundary, which comprises three corners and three sides, i.e., six geometrical elements, and 9/6 = 3/2. Notice that for the root edge, the ratio of the number of yods (4) to the number of geometrical elements (3) is 4/3, which is the tone ratio of the perfect fourth! As the number of yods surrounding the centre of an nth-order N-gon = ynN − 1 = (3/2)(3n+1)N and the number of geometrical elements surrounding its centre = gnN − 1 = (3n+1)N, the ratio of these two numbers for any nth-order N-gon is 3/2, whatever the values of n and N. In view of this property for individual polygons, it is not remarkable that the ratio of the sums of these two quantities for all seven separate, nth-order polygons is also 3/2. Indeed, it is true for any set of separate polygons, not just for those that make up the inner Tree of Life. What is non-trivial is that this same ratio applies to the populations of all yods and geometrical elements in the seven regular polygons when they are enfolded. 31 yods disappear when the separate polygons become enfolded, so that the yod population of 295 is reduced to 264. Twenty-three geometrical elements disappear, so that the 199 geometrical elements become 176 elements. The 288 yods surrounding the centres of the seven separate polygons become the 257 yods that surround the centres of the seven enfolded polygons, whilst the 192 geometrical elements surrounding centres of the seven separate polygons become 169 geometrical elements surrounding their centres when enfolded. Despite this disappearance, the fraction 3/2 survives the enfoldment, this time as the ratio of the total populations of yods and geometrical elements instead of as the ratio of numbers of yods and elements surrounding centres of the seven separate polygons (notice that 288/192 = 3/2 but 257/169 ≠ 3/2, whereas 264/176 = 3/2)! This would not happen for any set of polygons. In fact, the property exists only for a set of enfolded polygons that includes either a pentagon & decagon or a triangle, pentagon, hexagon & decagon (as in the case of the inner Tree of Life).**
As Yn = 3Sn, the number of yods in two separate sets of seven enfolded polygons ≡ Y′ = 2Yn = 6Sn and their number of geometrical elements ≡ G′ = 2Gn = 4Sn. Therefore,
Y’/G′ = 3/2
and
G′/Yn = 4/3.
This is the tone ratio of the perfect fourth in music. The ratio Y′/Yn = 2 corresponds to the octave. These three ratios are the ratios generated by the tetractys in the historical context of Pythagoras' contribution to music theory that is well-known to students of music and science:
|
|
|
What is the corresponding relation between the yod (Y) and geometrical (G) populations of the (7+7) enfolded polygons? As
Y = 2Yn − 4
and
G = 2Gn − 3,
we find that
2Y = 3G + 1.
This compares with the relation
2Yn = 3Gn
for the seven enfolded, nth-order, regular polygons making up half of the inner form of the Tree of Life. As Y = 2Yn − 4, G = 2Gn − 3, Yn = 3Sn and Gn = 2Sn,
Y = 6Sn − 4
and
G = 4Sn − 3.
The total number of sides in the (7+7) enfolded polygons ≡ S = 2Sn − 1 = 34 + 47×3n. Therefore,
Y = 3S − 1
and
G = 2S − 1,
so that
Y/G = (3S−1)/(2S−1).
This may be simplified to:
Y/G = 3/2 + ½(2S−1)−1.
As n→∞, S→∞ and Y/G→3/2. The ratio of the yod & geometrical populations of the complete inner form of the Tree of Life is larger than the fraction 3/2 but reduces as n→∞ from its maximum value of 524/349 when n = 1 to 3/2 as its asymptotic limit for an infinitely populated inner Tree of Life. This amounts only to a decrease of about 0.095%. Even when n = 1, the ratio is only about 0.1% above 3/2. But, for the seven enfolded polygons, the ratio remains exactly 3/2 for all values of n.
In terms of their number (C) of corners of their T triangles, G = C + S + T. Therefore,
C + S + T = 2S − 1,
so that
S = C + T + 1.
If we define S′ as the number of sides outside the root edge of the (7+7) enfolded, nth-order polygons, then S′ = S − 1. This means that
S′ = C + T.
We find that the number of external sides is equal to the number of their 0th-order triangles and their corners. This is a remarkable, geometrical property of the inner form of the Tree of Life. Therefore, as G = C + S + T,
G = S + S′.
The number of geometrical elements in the inner Tree of Life is the sum of the number of sides of all its triangles and the number outside the root edge shared by the (7+7) enfolded polygons. The figures in Table 10 illustrate this:
349 = 175 + 174.
913 = 457 + 456.
2605 = 1303 + 1302.
7681 = 3841 + 3840.
"Intrinsic yods" are discussed in many pages of this website. They are defined as all the yods in the inner form of the Tree of Life except the topmost corners of the two hexagons, which are shared with the lowest corners of the two hexagons belonging to the inner form of the next higher, overlapping Tree of Life. Intrinsic yods are those unshared yods that solely make up the inner form of each successive Tree. "Intrinsic geometrical elements" are, similarly, discussed many times. They are all those elements, apart from the topmost, shared corners of the pair of hexagons, that uniquely shape the inner form of each overlapping Tree because they are unshared with polygons enfolded in the next higher Tree of Life. Two other sets of yods and geometrical elements may be defined: 1. the yods or geometrical elements outside the root edge that create the form of the inner Tree of Life, and 2. the intrinsic yods or geometrical elements outside the root edge. Table 11 lists the relations between the populations of these types of yods and geometrical elements in the seven enfolded polygons and the (7+7) enfolded polygons (n.b. the subscript n is dropped from symbols because the relation: 2Yn = 3Gn holds whatever the value of n, although both populations are, of course, functions of n. But, for the purpose of Table 11, the change of symbols: Yn→y & Gn→g will be made, with Y & G still referring to the (7+7) enfolded polygons).
Table 11
|
7 enfolded polygons |
(7+7) enfolded polygons |
|
| Number of yods Number of geometrical elements Relation: |
y |
Y = 2y − 4 |
|
Number of yods outside root edge |
y′ ≡ y − 4 |
Y′ ≡ Y − 4 |
| Number of intrinsic yods Number of intrinsic geometrical elements Relation: |
y0 ≡ y − 1 |
Y0 ≡ Y − 2 |
| Number of intrinsic yods outside root edge Number of intrinsic geometrical elements outside root edge Relation: |
ŷ ≡ y0 − 4 |
Ŷ ≡ Y0 − 4 |
Notice in Table 11 that the relations between types of populations contain only the Pythagorean integers 1, 2, 3 & 4 expressed by the four rows of the tetractys. In particular, these integers are the constant that appears in the relations for the complete inner form of the Tree of Life. Their presence is indicating that these four classes of yods and geometrical elements are special. Much of the analysis in the pages of this website is devoted to them because they generate numbers and patterns that manifest in the group mathematics of E8×E8 and in the remote-viewing accounts of superstrings given over a century ago by Annie Besant & C.W. Leadbeater (see Occult Chemistry), as well as in the seven musical diatonic scales and in the correspondences between the inner form of the Tree of Life and other sacred geometries, as described in Correspondences and Wonders of correspondences.
The number of yods that line the Sn sides of the Tn triangles in Pn ≡ Bn = Cn + 2Sn. As Gn = 2Sn,
Bn = Cn + Gn = ½(105 + 329×3n−1).
The number of boundary yods in the (7+7) enfolded nth-order polygons = 2Bn − 4 = 101 + 329×3n−1. Table 12 lists the boundary yods for n = 1, 2, 3 & 4:
Table 12
|
7 enfolded polygons |
(7+7) enfolded polygons |
|||||||
|
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 1 |
n = 2 |
n = 3 |
n = 4 |
|
| Number of boundary yods | 217 | 546 | 1533 | 4494 | 430 | 1088 | 3062 | 8984 |
In particular, the number of boundary yods shaping the seven enfolded, 4th-order polygons outside their root edge = 4494 − 4 = 4490 = 449×10, where 449 is the 87th prime number and 87 is the number value of Levanah, the Mundane Chakra of Yesod.
As the top corners of both hexagons in the (7+7) polygons enfolded in a given Tree of Life coincide with the lowest corners of the hexagons enfolded in the next higher, overlapping Tree of Life, there are (430−2=428) yods lining the (7+7) enfolded 1st-order polygons that are intrinsic to them. This is the number value of Chasmalim, the Order of Angels assigned to Chesed. Table 12 indicates that 217 yods line the seven enfolded polygons. (217−1=216) intrinsic yods line the 88 sides of the 47 tetractyses making up each set of enfolded 1st-order polygons with 36 corners, where 216 is the number value of Geburah and 36 is the number value of ELOHA, its Godname.
Geometrical and yod compositions of the combined outer & inner forms of N Trees of Life/N-tree with nth-order polygons
When the outer form of the Tree of Life combines with its inner form, the number of geometrical elements or yods in the combination is not the sum of the respective numbers of both forms. This is because certain elements and yods coincide when they combine. They are indicated in the diagram below as blue yods and lines. Remembering that the plane occupied by the (7+7) enfolded polygons is that formed by the outer Pillars of the Tree of Life, each nth-order hexagon has six yods (two of which are corners) and two vertical sides of sectors that are shared with the Pillars of Judgement and Mercy and the horizontal Path joining Chesed and Geburah. Each enfolded nth-order triangle that occupies one of the sectors of each hexagon has one corner and one centre that coincide with yods in the outer Tree. It means that 16 yods (including six corners of triangles) and four sides are shared by the outer and inner forms of the Tree of Life, so that the combination needs 16 yods and 10 geometrical elements (six corners & four sides) to be subtracted from the sums of the respective, separate populations.
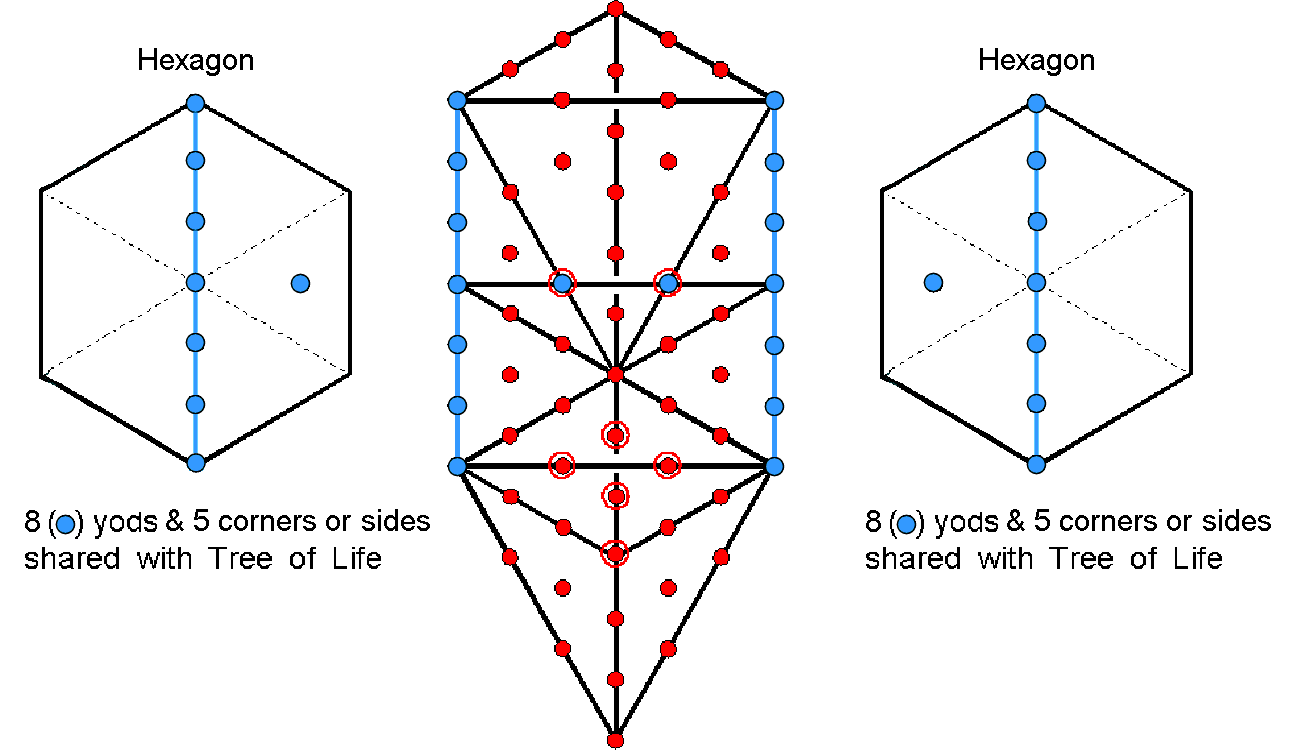
For mathematical consistency, when the inner form of the Tree of Life is regarded as composed of 14 nth-order polygons, the triangles making up its outer form must be regarded only as nth-order. It would be inconsistent to combine 1st-order polygons with 0th-order triangles in the outer Tree as shown in the diagram, which is intended merely to display what yods and what geometrical elements become shared during the combination of the outer and inner forms — whatever the common order of their polygons and triangles. This consistency must be maintained when the outer and inner forms of N overlapping Trees or the N-tree are considered. What also must be considered is the fact that the two blue hexagonal yods on the Chesed-Geburah Path remain hexagonal yods, whatever the order of the triangles in the outer Tree of Life, whereas the blue yod (with which they coincide) at the centre of each triangle in the (7+7) polygons remains a corner of a 0th-order triangle, whatever the order of these polygons. It means that there are two unique yods in the combined outer & inner forms of the Tree of Life (and for every overlapping Tree) that are hexagonal yods with respect to its outer form but which are corners with respect to its inner form. Their dual status must be taken into account in calculating the hexagonal yod population of the combined Trees. Finally, the topmost corners of the two hexagons enfolded in a given Tree of Life coincide with the lowest corners of the two hexagons enfolded in the next higher Tree. This means that the number of yods shared by the outer and inner forms of N overlapping Trees of Life is 14N + 2, where "2" denotes the topmost corners of the two hexagons enfolded in the Nth Tree. It also means that the number of geometrical elements shared by both forms is 8N + 2. Both these quantities need to be subtracted from the sum of the separate populations of yods and geometrical elements to avoid double-counting when the two forms are combined.
Using Tables 3, 6 & 8, the calculated yod and geometrical compositions of the combined outer and inner forms of N Trees/N-tree when the former have nth-order triangles and the latter have nth-order polygons are shown in Table 13:
Table 13. Numbers of corners, geometrical elements & yods in combined forms of N Trees/N-tree.
|
Combined outer & inner forms |
||
| N Trees of Life | N-tree | |
| Number of corners |
2 + 27N + (65N+6)×3n−1 |
½[3 + 54N + (130N+21)×3n−1] |
| Number of geometrical elements | 2 + 55N + 2(65N+6)×3n | 2 + 55N + (130N+21)×3n |
| Number of hexagonal yods | 54N + 8(65N+6)×3n−1 | 54N − 3 + (520N+84)×3n−1 |
| Number of yods |
2 + 81N + (65N+6)×3n+1 |
½ [162N − 3 + (130N+21)×3n+1] |
Notice that ADONAI, the Godname of Malkuth with number value 65, prescribes the yod population of the combined outer & inner forms of N Trees of Life, as well as their number of corners and geometrical elements, the number 130 being the 65th even integer. Here is remarkable evidence that the ancient Hebrew Divine Names determine through their gematria number values the very mathematical nature of the cosmic blueprint called the "Tree of Life."
The increase in yods from N Trees to (N+1) Trees = 81 + 65×3n+1. For n = 1, the increase is 666. This is the 36th triangular number, showing how ELOHA, the Godname of Geburah with number value 36, measures how many yods are needed to build the outer and inner forms of successive Trees of Life. The average number of hexagonal yods that surround the axes of the five Platonic solids in their faces and interiors is 666 (see bottom of page here).
Table 14 lists the populations of geometrical elements and yods in the Tree of Life and the 1-tree for 1st-, 2nd-, 3rd- & 4th-order triangles/polygons:
Table 14
| Combined outer & inner forms | ||||||||
|
Tree of Life |
1-tree |
|||||||
|
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 1 |
n = 2 |
n = 3 |
n = 4 |
|
| Number of corners | 100 | 242 | 668 | 1946 | 104 | 255 | 708 | 2067 |
| Number of geometrical elements | 483 | 1335 | 3891 | 11559 | 510 | 1416 | 4134 | 12288 |
| Number of hexagonal yods | 622 | 1758 | 5166 | 15390 | 655 | 1863 | 5487 | 16359 |
| Number of yods | 722 | 2000 | 5834 | 17336 | 759 | 2118 | 6195 | 18426 |
The combined outer & inner forms of the Tree of Life with 1st-order triangles and polygons comprise 483 geometrical elements. Of these, three make up the root edge, so that 480 elements are outside it. This number is a characteristic parameter of holistic systems, e.g., the 480 hexagonal yods in the (7+7) separate polygons of the inner Tree of Life (see #21) and the 480 hexagonal yods in the faces of the first four Platonic solids constructed from tetractyses (see here). In the case of the E8×E8 heterotic superstring, it is the number of roots of E8×E8 (see under heading "Superstring gauge symmetry group" here).
As the 1-tree shares 10 geometrical elements with its inner form (namely, the three corners and two sides lining the Pillars of Mercy & Judgement), the combined forms comprise 510 geometrical elements, of which 500 (=50×10) are unshared by either form. This shows how ELOHIM, the Godname of Binah with number value 50, prescribes the combined, outer & inner forms of the 1-tree.
Of the 622 hexagonal yods in the combined forms of the Tree of Life made up of 1st-order triangles and polygons, two belong to the root edge. 620 hexagonal yods are outside it. This number is the number value of Kether (see #7). Of the total of 722 yods, two hexagonal yods lie on the root edge, leaving 720 yods that comprise 100 corners and 620 hexagonal yods. This 100:620 division of the number 720 is identical to that displayed by the decagon when its sectors are 2nd-order tetractyses:
|
|
|
|
|
|
Its 100 tetractyses have 720 yods surrounding its centre. They comprise 100 corners and 620 hexagonal yods. This embodiment of the gematria number value 620 of Kether (the first of the 10 Sephiroth) by two 10-fold representations of God, one Kabbalistic, the other of a Pythagorean character, demonstrates the mathematical parallels between different sacred geometries when they are truly such. See here for further analysis of how the combined Trees of Life embody this number, as well as other Kabbalistic numbers. Other examples of the embodiment of the number 720 by sacred geometries are:
the number of sides of triangles in an nth-order N-gon ≡ snN = ½(3n+1)N,
and the number of triangles in an nth-order N-gon ≡ tnN = 3n−1N.
Therefore,
cnN + tnN = ½(3n−1+1)N + 3n−1N = ½(3n+1)N = snN
and
cnN + snN + tnN = 2snN.
** Proof: consider a set P of m different, separate nth-order polygons with N corners. According to Table 8, the number of yods in an nth-order r-gon = ynr = (3/2)(3n+1)r + 1.
Number of geometrical elements = gnr = (3n+1)r + 1.
Number of yods in P ≡ Y = ∑ynr = (3/2)(3n+1)N + m.
Number of geometrical elements in P ≡ G = ∑gnr = (3n+1)N + m.
The ratio (Y−m)/(G−m) of the numbers of yods and geometrical elements surrounding the centres of the m separate nth-order polygons is always 3/2. Suppose that p yods and q geometrical elements outside the sides that merge into the root edge vanish when the m polygons become enfolded. These are not the total numbers that vanish because the 4(m−1) yods and 3(m−1) geometrical elements making up the (m−1) sides that merge into the root edge of the enfolded polygons disappear as well.
Number of yods in m enfolded nth-order polygons ≡ Yn(m) = Y − p − 4(m−1) = (3/2)(3n+1)N + 4 − 3m − p.
Number of geometrical elements in m enfolded polygons ≡ Gn(m) = G − q − 3(m−1) = (3n+1)N + 3 − 2m − q.
Therefore, Yn(m)/Gn(m) = 3/2 if 3q − 2p = 1. Yods and geometrical elements can disappear only for two pairs of polygons: triangle-hexagon (let us call it "pair 1") and pentagon-decagon ("pair 2"). This is because the triangle takes the place of one sector of the hexagon, sharing six yods and four geometrical elements, and a corner of the pentagon coincides with the centre of the decagon, so that one yod and one geometrical element disappears when they become enfolded. Either p = 1 (P includes only pair 2), 6 (P includes only pair 1) or 7 (P includes pairs 1 & 2) and q = 1 (P includes pair 2), 4 (P includes pair 1) or 5 (P includes pairs 1 & 2). The relation between p and q:
3q − 2p = 1
derived above does not hold for p = 0 = q, so that P must include at least one of the two pairs of polygons that share yods and geometrical elements. Therefore, Yn(m)/gn(m) = 3/2 only if P includes:
It is concluded that Yn(m)/Gn(m) = 3/2 only if P includes either pair 2 (but not pair 1) or both pairs, i.e., m≥2. In the case of the inner Tree of Life, the 14 enfolded polygons have 70 corners that correspond to the 70 yods in the outer Tree of Life constructed from tetractyses. This means that either set of seven enfolded polygons has 36 corners. If we insist that the 2m enfolded polygons must have 70 corners to match the 70 yods, then the m enfolded polygons must have 36 corners. Separate, they have N corners; when enfolded, they have [N − 2(m−1)] corners because (m−1) sides disappear into the root edge. Therefore,
36 = N − 2(m−1) = N − 2m + 2,
so that
N = 34 + 2m.
As m≥2, N≥38. P cannot be just pair 2, because they have only 15 corners. Nor can it be just pair 1 & pair 2, because they have only 24 corners. This means that m>2 and N>38. As the polygons must include the pentagon and the decagon, the remaining (m−2) separate polygons must have more than (38−15=23) corners. If they include both pairs of polygons, m>4 and N>(34+8=42), so that the remaining (m−4) separate polygons must have more than (42−24=18) corners.
The 1-tree has 80 yods (see #40). They are matched by the 80 corners of the 94 sectors of the (7+7) enfolded polygons. If we insist that the 2m enfolded polygons must have sectors with 80 corners, then each set of m enfolded polygons must have sectors with 41 corners. Suppose that the centres of A polygons coincide with their corners when enfolded. As P must include at least pair 2, A = 1 if P includes only pair 2 (m>2) and A = 2 if it includes both pairs (m>4). Separate, the sectors of the polygons have (N+m) corners; when enfolded, they have [N − 2(m−1) + m − A] corners. Therefore,
41 = N + 2 − m − A,
so that
N = 39 + m + A.
But
m + A > 3 (P includes only pair 2)
> 6 (P includes pairs 1 & 2).
This means that either N>42, so that the remaining (m−2) polygons must have more than (42−15=27) corners, or N>45, so that the remaining (m−4) polygons must have more than (45−24=21) corners. If we insist that the 2m enfolded polygons have 70 corners and that their sectors have 80 corners, then P must include the pentagon and the decagon and the remaining (m−2) polygons must have more than 27 corners, or else it must include the triangle, pentagon, hexagon & decagon and the remaining (m−4) polygons must have more than 21 corners. In the case of the inner Tree of Life, the three remaining polygons (square, octagon & dodecagon) have 24 corners and so, as expected, the seven enfolded polygons display the property: Yn(m)/Gn(m) = 3/2.
As
N = 34 + 2m = 39 + m + A,
m − A = 5.
As A = 1 or 2, m = 6 or 7 and m + A = 7 or 9. This means that N = 46 or 48. The latter possibility is displayed by the seven polygons making up the inner Tree of Life.
| << Previous 1... 41 42 43 44 [45] Next >> |