| << Previous 1 [2] 3 4 5 ...45 Next >> |

The tone ratio n of a musical note is the ratio of its frequency, or pitch, as a sound wave to the frequency of the first note C, or "tonic," of an arbitrarily chosen octave of notes C-C′. The tone ratio of the tonic is therefore 1, so that 1≤n≤2 for all notes in the same octave. Because it is a relative measure, the tone ratios n, 2n, 22n, etc of successive octaves of a note relative to the tonics of these octaves with tone ratios 1, 2, 22, etc do not alter; they still have the value n. The tone ratios of various octaves of a note vary only with respective to some arbitrarily chosen, fixed note. The interval between two notes with tone ratios n & m (m>n) is the ratio m/n of their tone ratios. The set of intervals between the eight notes in a given octave is the same whatever the octave, for the interval between these two notes in the Nth octave is 2Nm/2Nn, which is m/n.
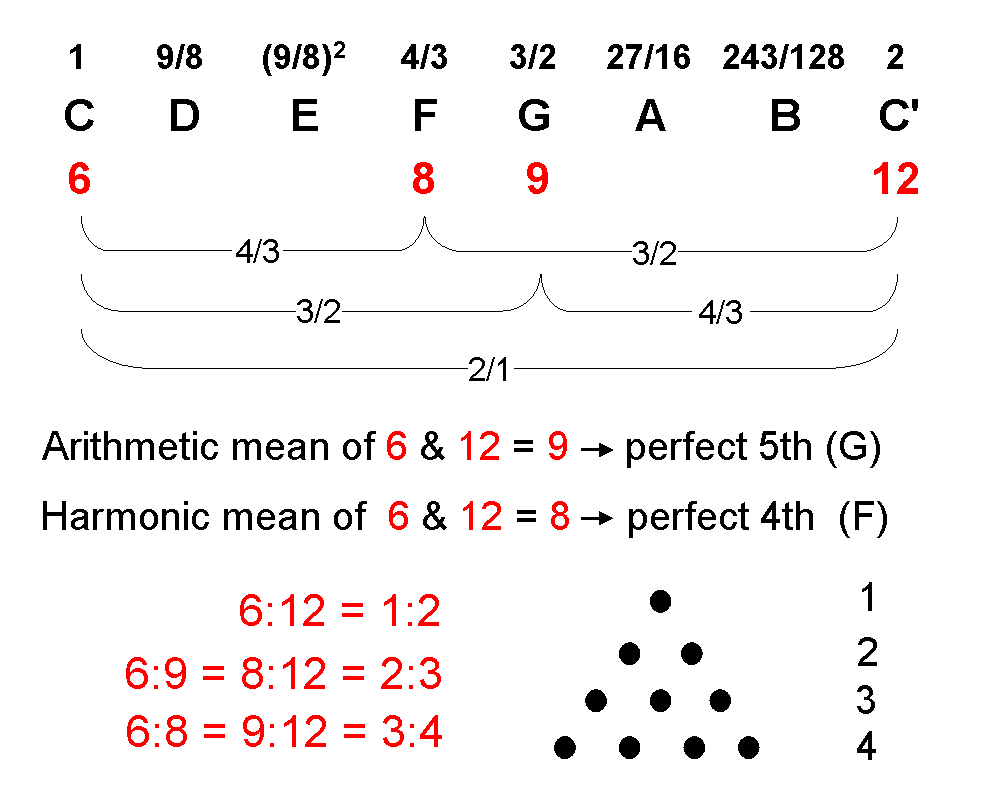
Consider the numbers 6, 8, 9 & 12. The arithmetic mean of two number a & b is a third number A for which
(b−A)/(A−a) = 1.
9 is the arithmetic mean of 6 & 12 because 12 − 9 = 3 = 9 − 6. It determines the perfect fifth G (so-called because it is the fifth note of the Pythagorean musical scale). The harmonic mean of a & b is a number H for which
(b−H)/(H−a) = b/a.
8 is the harmonic mean of 6 & 12 because (12−8)/(8−6) = 4/2 = 2 = 12/6. It defines the perfect fourth F (so-called because it is the fourth note of the Pythagorean scale). As 9/6 = 3/2, this is the tone ratio of G. As 8/6 = 4/3, this is the tone ratio of F. The interval between two notes with tone ratios n & m (m>n) is the ratio m/n of its tone ratios. The interval between G & F is 9/8, which is the ratio of the arithmetic & geometric means of 6 & 12. This is the tone ratio of the second note D in the Pythagorean scale. The tone ratios 2/1, 3/2 & 4/3 are expressed by the four integers 1, 2, 3 & 4 symbolized by the four rows of 1, 2, 3 & 4 dots in the Pythagorean tetractys.
As the next page shows, the tone ratios of the eight notes of the Pythagorean scale:
| 1 | 9/8 | (9/8)2 | 4/3 | 3/2 | 27/16 | 243/128 | 2 |
are generated by successive jumps or drops in intervals of a perfect fourth or perfect fifth.
| << Previous 1 [2] 3 4 5 ...45 Next >> |