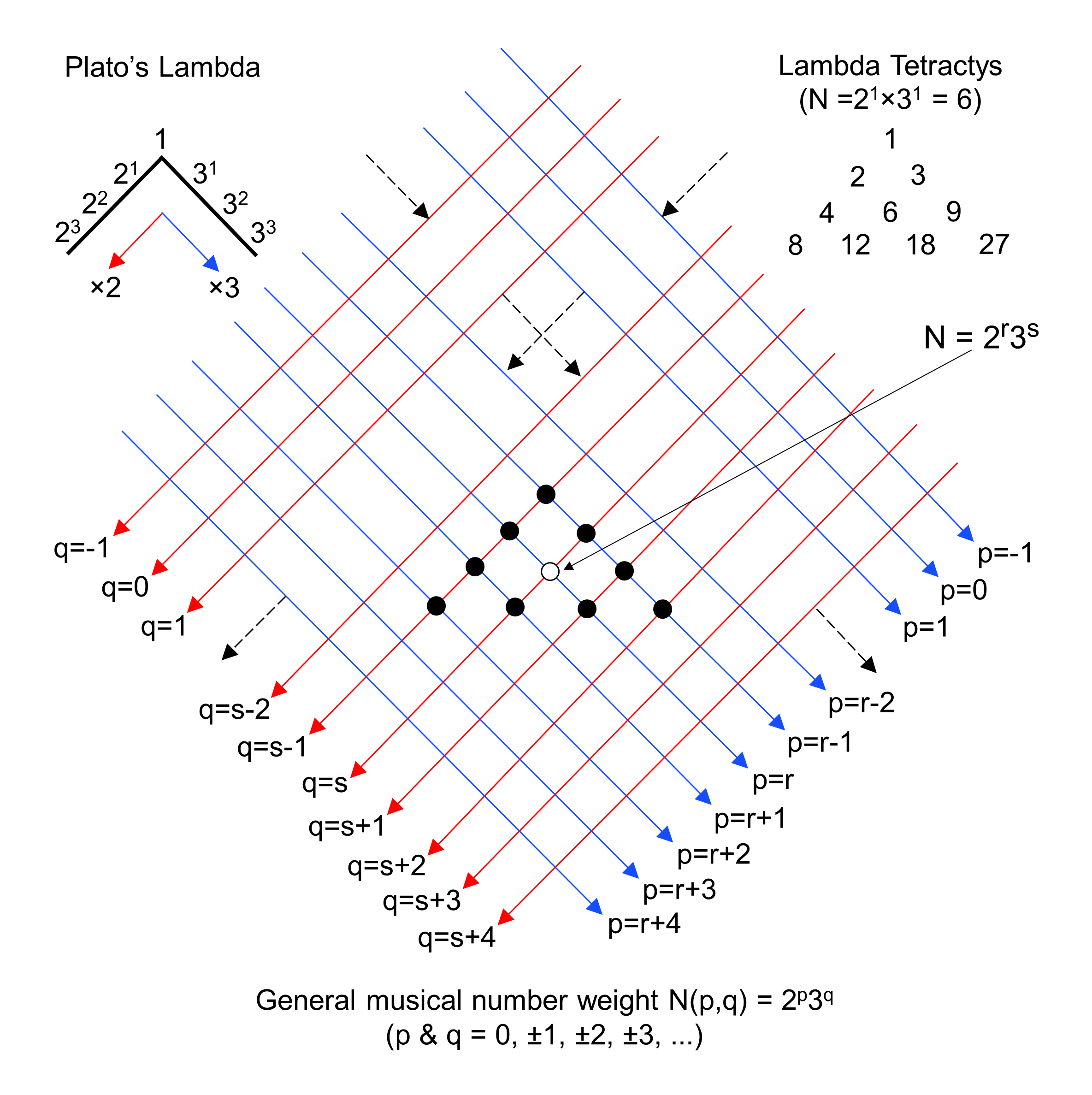
Figure 1. The generalised Lambda Tetractys (TN).
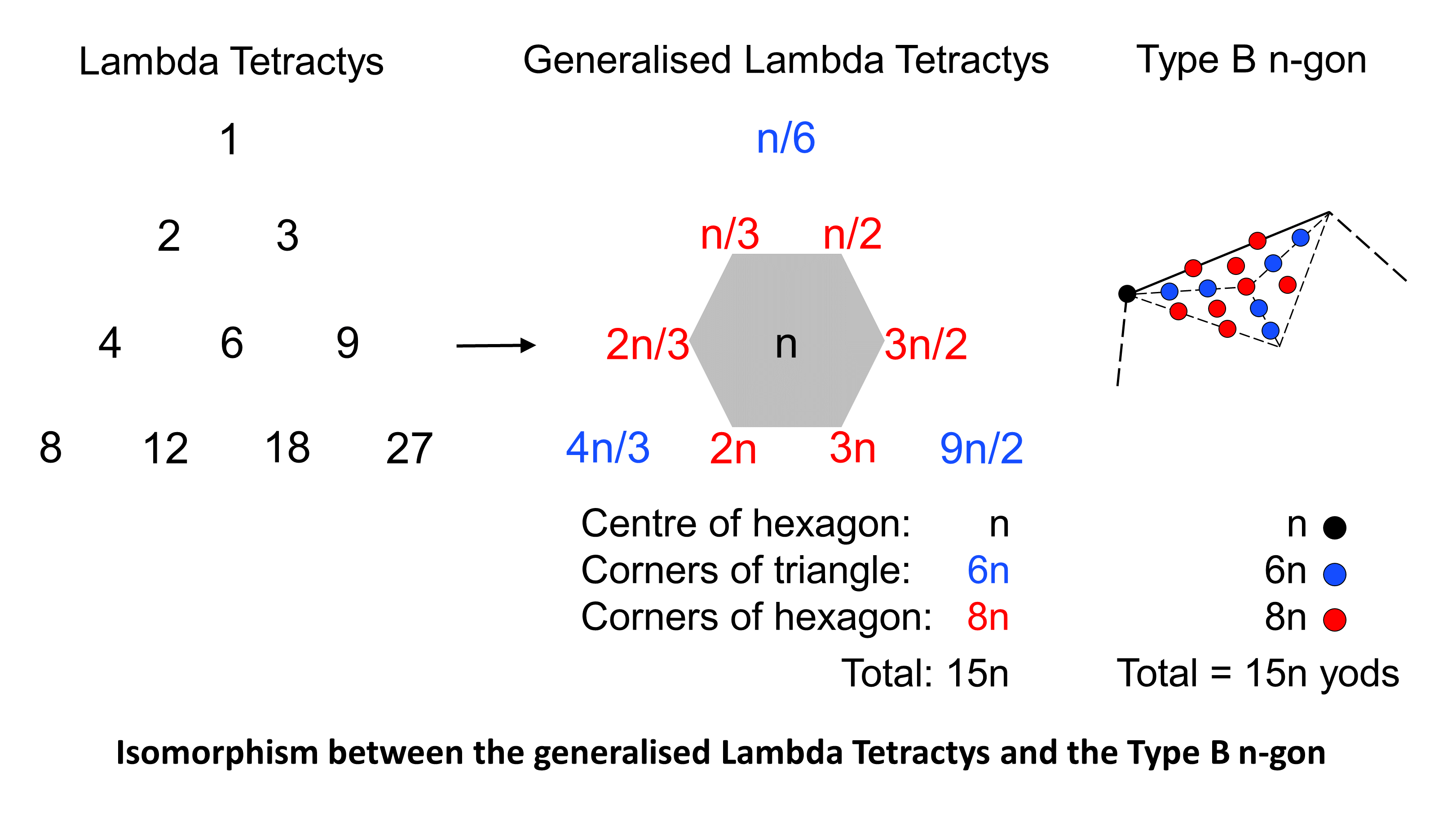
Figure 2. The Type B n-gon is isomorphic to the tetractys Tn of musical number weights with n at its centre.
| << Previous 1... 41 42 43 44 [45] Next >> |
The generalised Lambda Tetractys and its polygonal counterpart
The Lambda Tetractys is generated by adding the three numbers 6, 12 & 18 to the seven numbers lining the inclined sides of the lambda (Λ) shape into which Plato said in Timaeus, his treatise on cosmology, the Demiurge shaped and folded a strip of the World Soul and marked sections with lengths measured by these numbers from its folding point. Following the multiplicative factors of 2 and 3 that generate the first three terms after 1 of the geometric series 1, 2, 4, 8, ... and 1, 3, 9, 27, ... marked out on, respectively, the left-leaning and right-leaning sides of the lambda (indicated by the red and blue arrows), the central integer is 3×2=6, followed by 6×2=12 on the left and 6×3=18 on the right.
The Lambda Tetractys is merely one of the tetractyses of 10 numbers that can be drawn from an infinite, hexagonal lattice of numbers located at the intersections of one set of parallel straight lines (coloured red) with another set of parallel lines (coloured blue). Numbers arranged along red lines (Fig. 1) are members of the infinite geometric series 1, 2, 4, 8, ...with a geometric ratio of 2; numbers arranged along blue lines belong to the infinite geometrical series 1, 3, 9, ... with a geometric ratio
|
|
|
|
Figure 1. The generalised Lambda Tetractys (TN). |
Figure 2. The Type B n-gon is isomorphic to the tetractys Tn of musical number weights with n at its centre. |
of 3. The number located at the intersection of a red and a blue line has the form 2p3q (p & q = 0, ±1, ±2, ±3, ...). It is the centre of a tetractys TN of 10 numbers, each defined by different values of p and q. The central number 6 (=2×3) in the Lambda Tetractys has p = 1 = q. Numbers on the blue line p = r are defined by the same value r of p but have different values of q; numbers on the red line q = s are defined by the same value s of q but by different values of p. They intersect at the number N = 2r3s. The apex of TN is 2r-13s-1, i.e., N/6. This is N/6 times the number 1 at the apex of the Lambda Tetractys. In fact, every number in TN is N/6 times its counterpart in the Lambda Tetractys T6 (Fig. 2). Every tetractys centred on a given number N is the Lambda Tetractys with every one of its numbers N/6 times its counterpart in the latter. The ratio of any two number weights 2p3q and 2p′3q′ is 2p-p′3q-q′ = 2p′′3q′′, where p′′ = p - p′ and q′′ = q - q′. This is of the same form as any number weight, so that every number weight is also a tone ratio of a musical note. All tetractys arrays of number weights/tone ratios reduce to the fundamental pattern of the Lambda Tetractys.
As the sum of the 10 numbers of T6 is 90, the sum of the 10 numbers in TN = N/6×90 = 15N, where 15 is the gematria number value of YAH, the older version of the Godname assigned to Chokmah. A Type B N-gon is an N-gon whose sectors are Type A triangles with 19 yods. It has 15 yods per sector (Fig. 2), so that the centre of the Type B N-gon is surrounded by 15N yods. This is the sum of the 10 number weights in TN. A Type B N-gon can be associated with every number N (N≥3) in the infinite hexagonal lattice of musical number weights. The Lambda Tetractys T6 with 6 at its centre is associated with a Type B hexagon with six corners and 90 yods surrounding its centre. The sum of the blue-coloured numbers at the corners of TN = 6N; this is the number of blue hexagonal yods lining sides of tetractyses inside each sector. The sum of the red-coloured numbers in TN at the corners of the hexagon coloured grey in Figure 2 = 8N; this is the number of red yods that are either at the centre of each sector, hexagonal yods lining the sides of its three tetractyses or hexagonal yods at their centres. The sum of the nine numbers surrounding the central number N = 14N; this is the number of extra yods (apart from its centre) needed to turn an N-gon into a Type B N-gon.
We can add number weights only if we ignore their musical context, which requires that they be divided by one another in order to generate the tone ratio, or frequency, of one note relative to another. One context that does make addition of number weights meaningful was discussed in Article 11. The sum of the 10 integers of T6 is 90, which is the number of Trees of Life in CTOL above its lowest Tree, the central number 6 denoting the six Trees of Life above the latter that map the six subplanes of the physical plane above its lowest subplane. The sum of the numbers surrounding the centre of T6 is 84, which is the number of Trees of Life that map the 84 subplanes in the 12 planes of consciousness above the physical plane. Adding numbers in the Lambda Tetractys is equivalent to putting together various non-overlapping sections of CTOL above its lowest Tree of Life. The Type B hexagon has 90 yods surrounding its centre that symbolise the 90 subplanes/Trees of Life above the lowest one in CTOL. It is the polygonal counterpart of T6 and the polygonal representation of CTOL. The 36 yods surrounding the centre of the Type A hexagon correspond to the sum of the three numbers 6, 12 & 18 needed to be added to Plato's Lambda to form the Lambda Tetractys, and the extra 54 yods needed to turn the Type A hexagon into the Type B hexagon correspond to the sum (54) of the seven numbers in the Lambda.
The five Platonic solids provide another context that makes addition of musical number weights meaningful. They have 90 edges that correspond to the sum of the 10 numbers of T6:
| Tetrahedron | Octahedron | Cube | Icosahedron | Dodecahedron | Total | |
| Number of edges | 6 | 12 | 12 | 30 | 30 | 90 |
The six edges of the tetrahedron correspond to the number 6 at the centre of T6 and the 84 edges of the octahedron, cube, icosahedron & dodecahedron correspond to the sum (84) of the nine numbers on its boundary. Other possible individual correspondences between number weights and numbers of edges are:
12 edges of octahedron → 4 + 8;
12 edges of cube → 3 + 9;
30 edges of icosahedron → 1 + 2 + 27;
30 edges of dodecahedron → 12 + 18.
(NB, these correspondences are not unique in the arithmetic sense — other combinations of number weights are possible. The question of which set of combinations is the correct one may be left aside, as the crucial point being established here is that the number weights of the Lambda Tetractys do add up to the numbers of edges of the five Platonic solids). The 36:54 division in the numbers of T6 correspond to the 36 edges of the tetrahedron & icosahedron/dodecahedron and the 54 edges of the octahedron, cube & dodecahedron/icosahedron. All these correspondences exist because both the Platonic solids and the musical number weights constitute holistic systems, one of whose global parameters is the number 90 (other examples can be found in #44 of Wonders of Correspondences).
Another isomorphism between the generalised Lambda Tetractys and the Type B N-gon is as follows: the nine number weights surrounding the central number N in TN that add up to 14N can be divided into 10 combinations that sum to 7N:
|
7N |
7N | |
| 1 | N/6 + N/3 + 2N/3 + 4N/3 + 9N/2 | N/2 + 3N/2 + 2N + 3N |
| 2 | N/3 + 2N/3 + 3N/2 + 9N/2 | N/6 + N/2 + 4N/3 + 2N + 3N |
| 3 | N/6 + N/3 + N/2 + 3N/2 + 9N/2 | 2N/3 + 4N/3 + 2N + 3N |
| 4 | N/2 + 2N/3 + 4N/3 + 9N/2 | N/6 + N/3 + 3N/2 + 2N + 3N |
| 5 | N/6 + N/3 + 2N + 9N/2 | N/2 + 2N/3 + 4N/3 + 3N/2 + 3N |
The counterpart of this 7N:7N division in the Type B N-gon is the set of 7N yods other than corners either lining sides of its N sectors or at centres of its 3N tetractyses and the set of 7N yods lining sides of tetractyses inside its sectors, e.g., the red corner inside each sector of the N-gon in Figure 2 becomes blue. As before, the issue of which of the five possibilites listed above should be regarded as the correct pair of combinations, each adding to 7N, need not detain us. The table shows that, when N = 6, the sum of the nine numbers is 84, which divides into two combinations of numbers, each adding up to 42. The counterpart in the Platonic solids of this 42:42 division is the 42 edges of the octahedron & icosahedron/dodecahedron and the 42 edges of the cube & dodecahedron/icosahedron. The meaning of this division vis-à-vis CTOL is that one number 42 denotes the 42 Trees of Life above the 7-tree that map the 42 subplanes of the six superphysical planes, whilst the other one denotes the 42 Trees that map the 42 subplanes of the six cosmic superphysical planes (see #3 in Maps of reality/Cosmic Tetractys). Taken singly, the number weights of T6 determine tone ratios of musical notes; taken in combination, the numbers, as well as their sums, denote the numbers of Trees of Life in various sections of CTOL above the 7-tree that maps the physical plane. This interpretation of the number weights can be extended by noting that there are six SLs per Tree of Life in CTOL, so that, when N = 36 (p = 2, q = 2), the sum of the nine numbers of T36 that surround the number 36 = 14×36 = 504. This is the number of SLs in CTOL down to the top of the 7-tree. All SLs are the corners of triangles in CTOL, and the number of triangles in the N-tree = 12N + 4. Therefore, every overlapping Tree of Life is composed of 12 triangles. When N = 72, the sum of the nine numbers of the boundary of T72 = 14×72 = 14×6×12 = 84×12 = 1008, which is the number of triangles in the 84 Trees of Life above the 7-tree. The number weights 6, 36 & 72 generate, respectively, the number of Trees in CTOL above the 7-tree, the number of their SLs and the number of their triangles. The number weight 12 generates the number (168) of SLs on each pillar of CTOL above the 7-tree. The number weight 24 generates the number (336) of SLs in CTOL on the Pillars of Mercy & Judgement above the 7-tree.
The number 7 reflects the division of each plane into seven subplanes. The fact that there exist five pairs of combinations of number weights that, separately, add up to 7N corresponds to the division of CTOL into two equal numbers of superphysical planes: six above the physical plane with 42 subplanes and six above the cosmic physical plane (the 49-tree) with 42 subplanes. This is how the pattern of numbers determining all the notes of the Pythagorean musical scale and their intervals also maps the seven cosmic planes of consciousness. Plato's cosmology has a meaning that is more profound than the astronomical interpretation normally given to it. It was not merely that the sacred planets and stars moved in a celestial, musical harmony. The very spiritual cosmos itself — the true celestial sphere mapped by the 84 Trees of Life mapping all superphysical levels of reality — is patterned by the same numbers that generate the notes of the Pythagorean musical scale.
| << Previous 1... 41 42 43 44 [45] Next >> |